大渡河流域上游洪水预报及实时校正研究

张 艳，梁忠民，陈在妮，朱 阳，王 军

(1.河海大学水文水资源学院，江苏 南京 210098；2.国电大渡河流域水电开发有限公司，四川 成都 610041)

0 引 言

现有的分布式水文模型可大致分为概念性和具有物理基础的两大类。前者是用概化方法来描述水文过程，有一定物理基础，结构简单，实用性强，如斯坦福模型、水箱模型、新安江模型等；后者是用数学物理方程表述水文循环的各子过程[1]，又可分为以水动力学原理为基础的分布式模型，如SHE模型，以及以水文学原理为基础的分布式模型，如DBSIN模型[2]。大渡河流域属于半湿润-湿润地区，其植被状况较好，降雨径流具有蓄满产流的特点；因此，本研究选用分散式新安江模型建立洪水预报方案。

目前洪水预报实时校正方法大体可分为两类：一是终端误差校正，该方法不考虑洪水预报中间过程中的误差，直接对最终的预报误差进行校正，如自回归校正算法[3]、递推最小二乘法[4-5]等；二是过程误差校正，该方法是对洪水预报中间各个过程的状态变量进行校正，通过降低中间环节的误差以达到降低终端误差的目的，如卡尔曼滤波[6-7]、动态响应曲线法[8-9]等。大渡河流域上游为人迹罕至区，布站困难，雨量站稀疏，会引起较大的面雨量计算误差，降低洪水预报精度。鉴于此，本文在分散式新安江模型的基础上，采用动态响应校正法进行面雨量校正，通过反演修正面雨量以进一步提高洪水预报精度，为大渡河流域实时洪水预报提供参考。

1 模型与方法

1.1 新安江模型

新安江模型的理论基础是蓄满产流概念，适用于湿润和半湿润地区。实际应用中，常对新安江模型进行分散式处理，即对流域内各个子单元进行产汇流计算，得子单元出口流量过程，所有子单元出口流量通过马斯京根法逐级进行河网汇流演算至流域出口断面，最终得到整个流域的出流过程[10]。

新安江模型的结构主要分为4个层次：一，产流采用蓄满产流概念；二，蒸散发采用三层蒸散发计算模式；三，采用划分地表、壤中及地下径流的三水源结构；四，汇流分为坡面、河网和河道汇流三阶段[11]。新安江模型参数的物理意义比较明确，且都有相对应的合理的取值范围，故在国内水文预报中得到了普遍使用。

1.2 面雨量动态响应校正方法

流域水文模型可以概化为由输入、输出、参数和状态变量组成的系统。即

Q(t)=f[X(t)，θ，t]

(1)

式中，Q(t)为模型计算的流域出口断面流量过程；f(·)为模型运算；X(t)为模型的输入变量；θ为模型参数；t为时间。

本文只考虑对流域面雨量P的校正，因此上述系统方程可简写为

Q(P)=f(P)

(2)

将降雨作为自变量求全微分

(3)

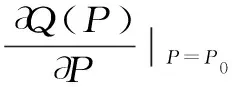
假设实测流量序列为Q(t)=[Q1，Q2，…，QL]T，则流量序列可以表达为

(4)

其矩阵形式为

Q(P)=Q(P0)+S·ΔP+E

(5)

式中，ΔP为面雨量误差的估计值；E为流量观测随机误差项，一般为服从零均值分布的白噪声向量；S为系统响应矩阵，其表达式为

(6)

移项可得

Q(P)-Q(P0)=S·(P-P0)+E

(7)

则面雨量误差与流量误差之间的系统响应关系为

EQ=S·EP+ε

(8)

式中，EQ为实测流量与计算流量的差值；EP为待求解的面雨量误差；ε为随机误差项。

面雨量误差的最小二乘估计值为

EP=(ST·S)-1·ST·EQ

(9)

则面雨量的校正值为

PD=P+EP

(10)

式中，PD为校正后的面雨量。

将校正后的面雨量重新输入新安江模型进行计算，即可得到校正后的流域出口断面流量过程。

2 应用研究

2.1 流域概况

大渡河是长江上游岷江水系的最大支流，地质地形条件复杂，多深切河谷。丹巴站是大渡河流域上游的一个重要节点，从地理位置和流域特性上来说，其径流的变化情况较大程度上直接反映了河源区的流量变化。丹巴以上流域范围为东经99°35′～102°55′，北纬30°17′～33°27′，控制面积为52 763 km2，约占大渡河流域总面积的68%。丹巴以上流域属川西高原气候区，干湿季分明、气温日变化大，降水量较少，平均年降水量一般仅600～700 mm左右，且集中在6月～9月，流域平均年径流量为400～500 mm。流域范围内有25个雨量站，雨量站网密度约为2 111 km2/站，远未达到我国SL 34—2013《水文站网规划技术导则》对雨量站网密度300 km2/站的一般性要求。流域内以丘状高原地貌为主，山顶平缓浑圆，谷底宽阔平坦，河流迂回曲折。

将丹巴以上流域划分为10个子流域，每个子流域再划分计算单元。选用流域内资料较为全面的2009年～2016年间20场历史洪水的降雨、蒸发和流量资料，每个子流域的模型输入降雨序列为其相应利用泰森多边形算法计算得到的面雨量序列，蒸发序列为全流域的平均蒸发序列，流量序列为各子流域出口断面的实测流量序列。参数率定采用SCE-UA算法自动优化与人工判别相互结合的方式，按流域拓扑顺序进行各子流域模型参数的率定与验证。其中，2009年～2014年为模型参数率定期，2015年至2016年为模型参数验证期。确定各子流域的模型参数后，按拓扑顺序建立丹巴以上流域洪水预报方案；最后，对丹巴出口断面的预报流量结合实测流量序列采用面雨量动态响应校正方法进行实时校正，从而构建起丹巴以上流域的洪水预报及实时校正模型。

为评估构建的洪水预报及实时校正模型的效果，采用以下3项指标：

(1)次洪径流深相对误差

ΔR=((Robs-Rc)/Robs)×100%

(11)

式中，Robs、Rc分别为实测次洪径流深、计算次洪径流深

(2)洪峰相对误差

ΔQm=((Qm，obs-Qm，c)/Qm，obs)×100%

(12)

式中，Qm,obs、Qm,c分别为实测洪峰、计算洪峰。

(3)确定性系数

(13)

2.2 结果分析

本文选用丹巴以上流域2009年～2016年共计20场洪水的降雨、蒸发和流量资料，利用构建的实时洪水预报及校正模型进行计算，所有模型参数在计算和校正过程中均保持不变，模型计算详细结果如表1所示。

从表1可以看出，新安江模型预报精度较高，20场历史洪水中有18场洪水的洪量、洪峰相对误差均在20%以内，平均确定性系数为0.70。采用面雨量校正方法校正后，洪量、洪峰相对误差有所降低，预报精度有明显提高，合格率从90%提高至100%。20场洪水的平均确定性系数由校正前的0.70提高到0.81，确定性系数大于0.5的历史洪水场次数由15场提高到19场；平均洪量相对误差由校正前的6.13%减小到5.31%；平均洪峰相对误差由校正前的7.62%减小到5.06%。

选用洪号为110701和110729的两场洪水作为典型说明校正效果。结果表明，面雨量校正后预报精度进一步提升。

总体而言，构建的实时洪水预报及校正模型在丹巴以上流域应用效果较好，面雨量校正方法能进一步提高洪水预报精度，可以用于该流域的实时洪水预报校正。

表1 丹巴以上流域历史洪水校正前后结果对比(全部洪水)

3 结 语

本文基于新安江模型及动态响应校正方法，建立了大渡河丹巴以上流域的实时洪水预报方案。结果表明，新安江模型在研究流域具有较好的适用性，模型模拟的合格率达90%；经过面雨量校正后，模型精度得到较大幅度地提升，合格率达100%，且面雨量校正方法不增加模型参数，也不损失预报的预见期，实用性强。本研究成果在丹巴以上流域的洪水预报中取得较好效果，所采用的模型与技术也可应用于大渡河流域其他断面的实时洪水预报工作，但如何进一步提高预报精度与可靠性，值得深入研究。