土质路基边坡临界滑动面的确定计算分析
陈臣
(重庆交通大学,重庆400074)
土质路基边坡的失稳滑塌在公路建设和运营中属于一种常见地质灾害,边坡稳定性定量分析是边坡加固设计和治理的研究基础,任何有效的加固处理措施都源自对边坡稳定安全系数和临界滑动面位置的合理确定[1]。一般将土质类边坡的稳定性问题假定为平面应变问题,将土质边坡的滑裂面简化为圆弧曲面[2]。通常采用极限平衡分析理论,利用瑞典法(Fellenius)、Bishop 法、Janbu 法、Spencer 法、Morgenstern-Price 法[3]。这些方法最大的差异在于条间相互作用力的考虑不同,会影响计算所得边坡的稳定性安全系数[4]。文中利用GEO-SLOPE 软件包中的SLOPE/W 程序对土质边坡的稳定性进行计算分析,确定路基边坡的潜在滑动面,采取有效的加固治理措施,将潜在的威胁扼杀在初步阶段。
1 计算分析理论
利用极限平衡理论计算分析边坡的稳定性时,认为土体遵从Mohr-Coulomb 破坏准则,由极限状态下土条受力和力矩的平衡来分析边坡稳定性[5]。极限平衡理论条分法的基本原理如下:取单位长度土质边坡按平面问题计算,假设土质路基边坡潜在的圆弧滑动面,如图1 所示。圆弧滑裂面为AD,圆心为O,半径为R,将滑坡土体ABCD 分成若干个土条,任一土条的受力情况,如图1 所示。
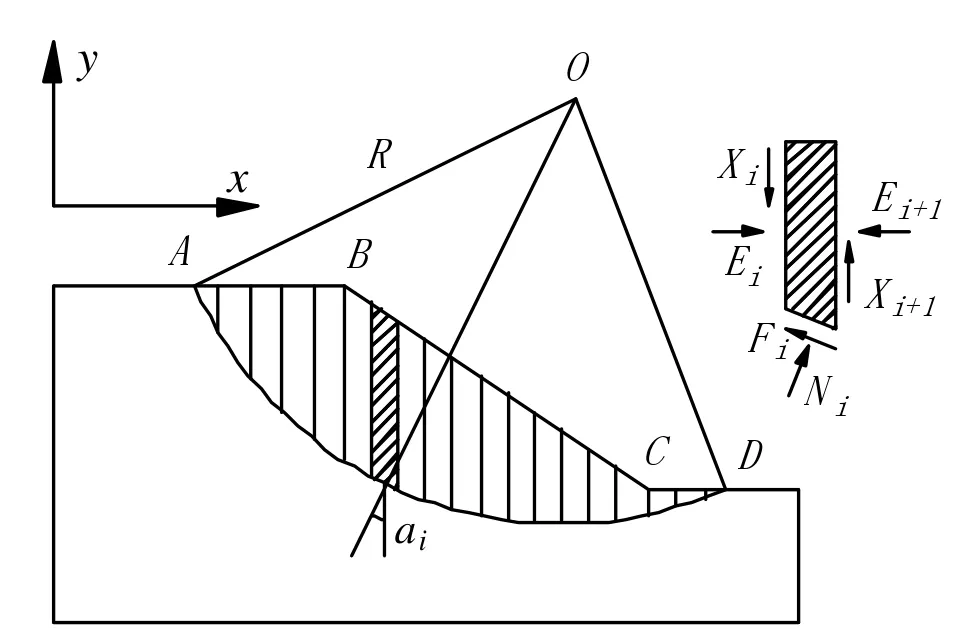
图1 条分法计算土质边坡稳定
由土条的受力情况可知,作用在土条上的力由5 个,但只能建立3 个平衡方程,因此必须做适当的假设求得Fi和Ni。瑞典条分法不考虑土条间相互作用力(即,Xi=Xi+1和Yi=Yi+1)。简化的Bishop 法只是考虑了土条间水平方向的相互作用力,忽略了竖向的作用力,并假定各土条底部滑动面上的抗滑系数均相同,为平均安全系数。
Janbu 法假定相邻土条间力合力作用点位置已知,这样就减少了n-1 个未知量。分析表明,作用的位置对土质边坡稳定性的影响不大[6],一般假定作用于土条底面以上高度1/3 处,作用点的连线成为推力线。
Spencer 法假定相邻土条间的法向力Ei与切向力Xi合力的倾角为一个待定的常数(即,Xi=Eitanθ,θ 为一常数)。
Morgenstern-Price 法首先对任意形状的滑裂面进行了分析,导出了满足力的平衡和力矩平衡的微分方程,假定条间法向力Ei与切向力Xi存在函数关系为Xi=λf(x)Ei。上述几种极限平衡理论条分法的推导过程,可参考文献[7,8]。
2 计算分析模型及计算结果
计算分析模型如图2 所示,计算时暂不考虑边坡坡顶的其他结构及荷载作用,整体边坡为均匀土质。图2 中给定边坡滑裂面的圆心坐标为(34.4,25.5),半径为20.2m。假设土质路基边坡的高度H 为10m,边坡的坡比为1:n=1:1.5;上层土体和下层土体重度、黏聚力和内摩擦角均相同,重度γs为18kN/m3,黏聚力c 为12kPa,内摩擦角φ 为24°。几种常用极限平衡条分方法所得边坡稳定安全系数,见表1。

图2 计算模型边坡
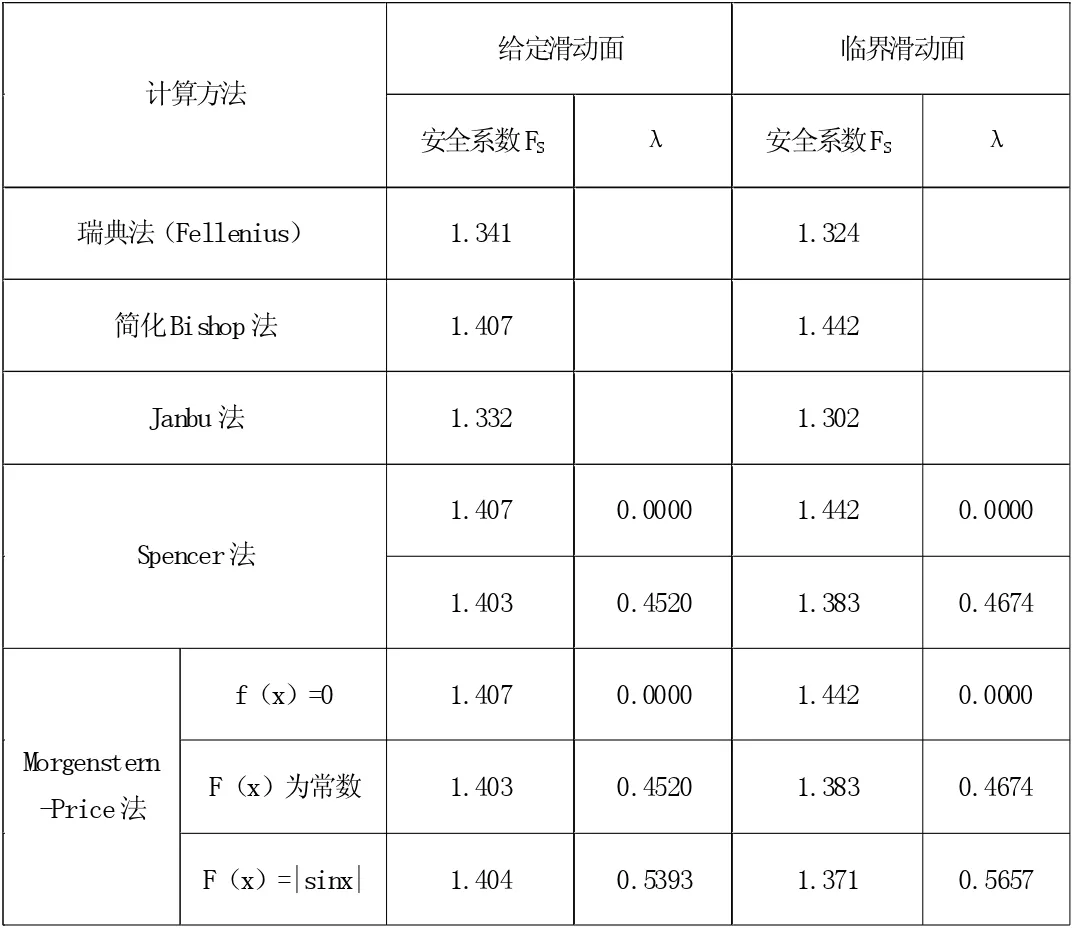
表1 算例边坡中常用极限平衡条分法安全系数比较
3 影响因素分析
通过Geo-Slope 软件进行数值模拟,边坡高度和土体强度参数一定的情况下,随着边坡高度的增加,潜在滑坡体的滑裂带均通过路基坡脚。由图3 可知,路基边坡的安全系数FS随着高度的增加而减小,且减小的幅度逐渐减弱,安全系数FS与边坡高度H 的关系曲线呈现出类似指数衰减的形状。
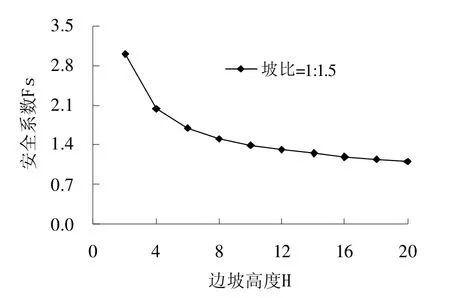
图3 安全系数FS 随边坡高度H 的变化关系
边坡坡比和土体强度参数一定的情况下,随着边坡坡比的减小(即,边坡坡度由陡到缓),潜在滑坡体的滑裂带逐渐由坡面向坡脚底部移动。由图4 可以看出,路基边坡的安全系数FS随着边坡坡度的减小而增大,且近似呈线性增加的关系。

图4 安全系数FS 随边坡坡比倒数m 的变化关系
4 结论
文中阐明了边坡稳定性分析几种常用的极限平衡条分法的差异,并比较分析了中它们的计算结果,并分析了几何参数对边坡稳定安全系数的影响,得到如下结论。
4.1 瑞典法与Janbu 法计算所得边坡安全系数较为接近;简化Bishop 法、Spencer 法和Morgenstern-Price 法计算所得边坡安全系数非常接近;瑞典法和Janbu 法所得结果与简化Bishop法相比,分别减小了4.7%和5.3%。
4.2 路基边坡安全系数随高度的增大而减小,且减小的幅度逐渐衰减;不同边坡高度情况下,边坡潜在的滑裂带均通过边坡坡脚。
4.3 随着边坡坡度减缓,边坡安全系数近似呈线性增加;边坡潜在的滑裂带逐渐由坡面移至坡脚底部。

