基于谱峭度的包络谱方法在滚动轴承故障诊断中的应用
赵黎 朱林 王丽芳 刘宏博


摘 要:共振解调法是滚动轴承故障诊断中最常用的方法之一, 然而其带通滤波器参数的选取通常比较困难。谱峭度法能根据峭度最大化原则自动确定带通滤波器参数,取得了一定的诊断效果。本文提出一种基于谱峭度的包络谱方法在滚动轴承故障诊断中的应用。首先利用谱峭度法选取最佳带通滤波器参数,然后通过带通滤波和包络解调进行故障特征提取,最后通过故障特征频率对滚动轴承故障进行定位。本文使用凯斯西储滚动轴承数据进行实验验证。
关键词:谱峭度;包络谱法;滚动轴承;故障特征提取
1谱峭度理论
峭度作为一种统计工具, 在噪声干扰较小的状态监测中, 可利用它对奇异信号的敏感性檢测系统的异常响应。但是,它作为一个全局指标无法反映特定信号分量的变化情况,不适合强噪声环境下的状态监测问题。为克服峭度在工程应用中的不足, Dwyer首先提出了谱峭度(Spectral Kurtosis-SK)法, 用于克服功率谱无法检测和提取信号中瞬态现象的问题。其基本思路是计算每根谱线的峭度值,从而发现隐藏的非平稳的存在,并确定它们出现在哪些频带。J.Antoni对此进行了深入研究, 阐述了谱峭度诊断机械故障的理论背景,给出了谱峭度的正式定义。
1.1谱峭度的定义
考虑非平稳信号的Wold-Cramer分解。定义Y(t)为由信号X(t)激励的系统响应。h(t,s)为时变冲击响应函数。则Y(t)可以表示为:
其中,是系统的时变传递函数。可以解释为信号Y(t)在频率处的复包络。在实际机械振动中,H(t,f)是随机的,可表示为,表示滤波器时变性的随机变量。基于四阶谱累积量的谱峭度定义为:
这里为2n 阶瞬时矩。是复包络能量的度量, 定义为:
因此, 谱峭度定义为能量归一化累积量, 即概率密度函数H的峰值度量。
2谱峭度检测滚动轴承故障的物理解释
滚动轴承通用的振动信号模型可用下式表示:
为实际测量的振动信号,为被检测的故障信号,为强烈的加性噪声。滚动轴承的潜在故障产生一系列重复的瞬时冲击力。从而激起系统的某些结构共振。合理的通用模型为:
是单个冲击引起的脉冲响应。和分别表示各个脉冲的随机幅值和发生时间。
文献[10]给出谱峭度的解释为:理想滤波器组的输出在频率f处计算得到的峭度值即为谱峭度。根据该文献的理论结果, 可以得到:
这里为的谱峭度,为噪信比,即,它是频率的函数,和分别为噪声和信号的功率谱密度。因此,在信噪比很高的频率处,近似等于,而在噪声很强烈的频率处,趋于零值。因此通过计算整个频域的谱
峭度,可以找到谱峭度最大的频带,即为故障信号所在的那些频带。
3滚动轴承故障特征提取算法
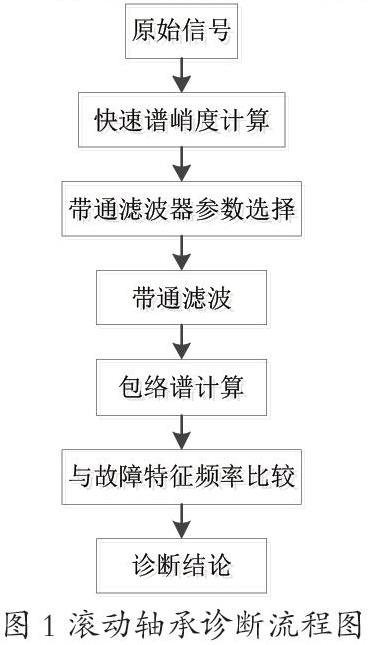
应用谱峭度理论诊断机械故障已取得了一定成效,利用谱峭度能自动确定带通滤波器的中心频率和带宽,突出高频共振分量,通过包络解调能够从高频分量中提取滚动轴承的低频故障特征频率。本文提出一种基于谱峭度的包络谱方法在滚动轴承故障诊断中的应用。具体诊断步骤如下,详细流程如图1 所示。
(1)对采集的原始信号进行快速峭度计算,选取峭度最大处对应的中心频率和带宽;(2)以该中心频率和带宽为带通滤波器参数对原始信号进行带通滤波;(3)对滤波后信号进行包络,并通过傅里叶变换求出包络谱;(4)将理论计算所得的滚动轴承故障特征频率与包络谱中所对应的频率进行比较,从而确定故障状态。
4实验研究
本文采用凯斯西储滚动轴承数据进行实验研究,其实验装置原理如图2所示,该装置由一个电机驱动轴旋转,扭矩传感器和编码器安装在轴上方,轴的扭矩通过测功器和电机控制系统进行控制。该实验用电火花加工的方法在风机端轴承和驱动端轴承的内环、外环、滚动体制造人为故障,采用压电式加速度传感器对振动信号进行采集,设置两种不同的采样频率,分别为12KHz和48KHz,电机工作在不同的转速下,分别为1797rpm、1772rpm、1750rpm、1722rpm。
选取一组电机转速为1750rpm,驱动端轴承的内环故障直径为0.36mm,采样率为48KHz的故障轴承数据进行方法验证。其时域信号如图3所示,从时域图中无法辨识故障类型,需要对其进一步分析。对原始信号进行快速峭度计算,其谱峭度图如图4所示。从图4中可以找出峭度最大值所对应的中心频率和带宽分别为9187.5Hz和375Hz,则带通滤波器的范围为[9000 9375]Hz, 在此范围内,峭度值最大,信噪比也最高,使用该滤波器对原信号滤波,再通过包络谱计算,其包络谱图如图5所示。从图5中可以找到157.9Hz的特征频率及其倍频,与理论计算所得的轴承内环特征频率基本一致,并且在内环的特征频率旁出现以轴承旋转频率为29.22Hz差频的边频,说明轴承的内环出现损坏。
滚动体的故障诊断过程最为复杂,为了说明该方法对滚动体故障诊断的有效性,选取一组滚动体故障数据进行分析,其转速为1722rpm,驱动端轴承滚动体故障直径为0.18mm,采样率为12KHz,其时域信号如图6所示。对原始信号进行快速峭度计算,其谱峭度图如图7所示,从图7中可以找出峭度最大值所对应的中心频率和带宽分别为1062.5Hz和125Hz,则带通滤波器的范围为[1000 1125]Hz,使用该滤波范围的滤波器对原始信号滤波,再通过包络谱计算,其包络谱图如图8所示。图8显示的电机转速的基频28.73Hz及其所对应的二倍频很明显,其 67.82Hz的特征频率与理论计算所得的轴承滚动体的特征频率基本一致,说明轴承的滚动体出现损坏。
前两组数据应用谱峭度的包络谱方法提取滚动轴承的内环和滚动体的故障特征频率明显,取得较好的效果。为了说明该方法适用的广泛性,最后再选取一组外环故障数据进行分析,其电机转速为1772rpm,风扇端轴承的外环故障直径为0.36mm,采样频率为12KHz,经综合分析,说明轴承的外环出现损坏。
5结论
滚动轴承的故障信号通常被强烈的背景噪声淹没,提取故障特征十分困难。因此需要从背景噪声中提取高频冲击成分,利用谱峭度可以突出信号高频共振成分,减少低频干扰,提高峭度值。共振解调是一种常用的滚动轴承故障诊断方法, 但其带通滤波器的选择通常需要操作者的经验和历史数据, 而谱峭度对隐藏于噪声中的瞬态冲击非常敏感, 可用于自動确定带通滤波器参数。本文应用基于谱峭度的包络谱方法对滚动轴承的内环、滚动体、外环进行故障特征进行提取,并利用凯斯西储滚动轴承数据进行实验验证,均取得较好的效果,为滚动轴承故障诊断的研究提供了一个新的途径。
参考文献:
[1] 梅宏斌. 滚动轴承振动监测与诊断-理论、方法 、系统[M] . 北京:机械工业出版社, 1996.
[2] 唐贵基,蔡伟.应用小波包和包络分析的滚动轴承故障诊断[J].振动、测试与诊断,2009,29(2):201—204.
[3]于德介,程军圣,杨宇。Hilbert-Huang变换在滚动轴承故障诊断中的应用[J].中国机械工程,2003(24):2140-2142.
[4] Y Yang,D Yu, J Cheng. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM [J]. Measurement, 2007, 40(9-10): 943-950.
[5] 程军圣,史美丽,杨宇.基于LMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2010,29(8):141-144.
[6] 苏文圣,王奉涛等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010(3):18-21.
[7] 张志刚,石晓辉等.基于改进EMD和谱峭度法滚动轴承故障特征提取[J].振动、测试与诊断,2013,33(3):478-482.
[8] Dwyer R F. Detection of non-Gaussian signals by frequency domain kurtosis estimation [C] .International Conference On Acoustics, Speech, and Signal Processing, Boston, 1983, 607 - 610.
[9] Antoni J. The spectral kurtosis: A useful tool for characterising non-stationary signals [J] .Mechanical Systems and Signal Processing, 2006, 20 :282 - 307.
[10] Antoni J, Randall R B, The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing, 2006, 20: 308 - 331.

