基于SAP2000的单层网壳屈曲分析

□□ 孙伟苹

(山西建筑职业技术学院,山西 晋中 030619)

引言

随着我国经济的发展，空间结构在工程中得到了广泛应用，由于网壳型空间结构造型优美，有独特的三维空间结构，受力性能及抗震性能明显优于混凝土结构，因而广泛应用于大跨度结构中，然而应用中往往会由于网壳局部或整体失稳而导致网壳破坏。本文主要对单层网壳分别在对初始应力为0和以恒载非线性分析结果作为初始状态进行屈曲分析，对比其屈曲临界荷载，为今后网壳稳定性的研究提供参考。

1 结构稳定性

结构的稳定性可分为3种类型：

(1)分枝点失稳

当结构或某构件没有任何缺陷能承受的荷载达到某个临界值时，结构或构件将处于除初始平衡状态外的新平衡状态，这种状态称为分枝点失稳或平衡分岔失稳。这时结构失稳的临界荷载称为屈曲荷载。由于这类失稳问题的求解属于数学上的特征值问题(类似于特征向量法的模态分析)，故也称为特征值屈曲分析。

(2)极值点失稳

非理想的结构或构件在荷载作用下产生的变形迅速增大并丧失承载力，称为极值点失稳。极值点失稳时的荷载称为极限荷载或压溃荷载，此类失稳不会产生新的变形形式，也叫平衡状态无质变。

(3)跳跃失稳

当结构或构件承受的荷载达到某一数值时，其平衡状态将直接跳跃到非临近的另一个平衡状态，因此称为跳跃失稳或跃越失稳。跳跃失稳并没有在极值点或分枝点，但突变的平衡状态同样会导致结构丧失承载力。

在工程中，理想或完善的结构并不存在，类似于初始曲率、参与应力或偏心加载等引起的失稳均属于极值点失稳，本文对单层网壳进行屈曲分析，第一种情况是初始应力为0进行的屈曲分析属于分枝点失稳；第二种情况以恒载非线性分析结果作为初始状态进行屈曲分析属于极值点失稳。

2 模型参数

模型采用单层凯威特型球面网壳，网壳跨度为20 000 mm，矢高为3 000 mm，球面半径为18 166.67 mm，支座采用铰接形式。该结构拟建于太原市，该地区抗震设防烈度为8度0.2g，地震设计分组为第二组，建筑场地类别拟设为Ⅲ类，计算时仅考虑水平地震作用，先采用3d3s进行截面设计，最后得到杆件截面共有3种，分别为Φ50×3.5、Φ60×3.5、Φ76×3.5。该网壳的用钢量为2.035 t，计算模型尺寸如图1所示。

图1 单层网壳结构几何模型

3 屈曲分析

3.1 初始应力为0的屈曲分析

3.1.1 屈曲模态分析

根据SAP2000软件对模型进行屈曲分析，在初始应力为0状态下得出单层网壳的前6阶屈曲模态，如图2所示，从图中可以看出，单层网壳前6阶失稳均为局部失稳。说明单层网壳在对称荷载作用下发生整体失稳的可能性较小。

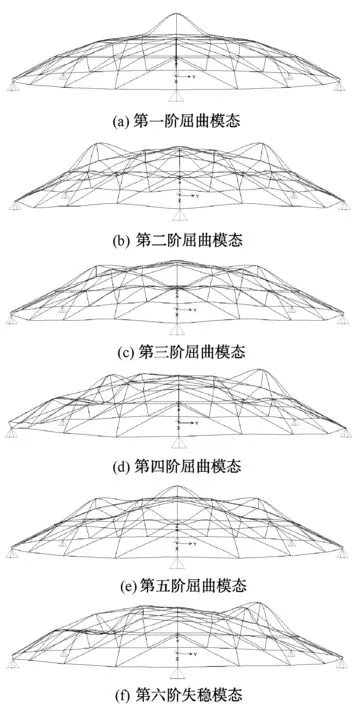
图2 初始应力为0状态下单层网壳前6阶屈曲模态

3.1.2 屈曲临界荷载分析

根据SAP2000软件对模型进行屈曲分析，在初始应力为0状态下得出单层网壳的前6阶屈曲模态对应的临界荷载值，见表1。从表1可以看出，单层网壳第1阶屈曲临界荷载最小，第2阶屈曲荷载至第6阶屈曲荷载比较接近，趋于稳定，这从失稳模态图中也能看出，图2(a)明显不同于图2(b)～图2(f)。

表1 初始应力为0状态下网壳屈曲临界荷载

3.2 恒载非线性分析结果为初始条件的屈曲分析

3.2.1 屈曲模态分析

根据SAP2000软件对模型进行屈曲分析，得出以恒载非线性分析结果为初始条件单层网壳的前6阶屈曲模态如图3所示。从图3中可以看出，单层网壳前6阶失稳均为局部失稳。说明单层网壳在对称荷载作用下发生整体失稳的可能性较小。

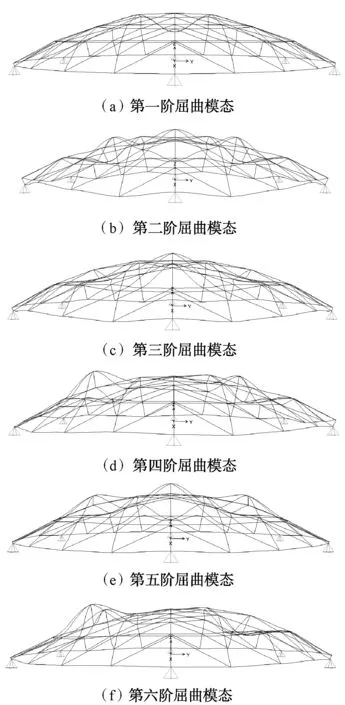
图3 以自重非线性分析结果为初始条件的网壳前6阶屈曲模态

3.2.2 屈曲临界荷载分析

根据SAP2000软件对模型进行屈曲分析，得出以恒载非线性分析结果为初始条件单层网壳的前6阶屈曲模态对应的临界荷载值，见表2。从表2可以看出，单层网壳第1阶屈曲临界荷载最小，第2阶屈曲荷载至第6阶屈曲荷载接近，趋于稳定，这从失稳模态图中也能看出，图3(a)明显不同于图3(b)～图3(f)。

表2 以自重非线性分析结果为初始条件的网壳屈曲临界荷载

4 结论

本文采用SAP2000软件对单层网壳进行屈曲分析，对比初始应力为0和初始状态为恒载非线性分析结果时的单层网壳屈曲分析，可得到以下结论：

4.1 单层网壳在外界荷载作用下发生局部失稳的可能性比较大。

4.2 以初始应力为0和以恒载非线性分析结果作为初始状态的单层网壳前6阶屈曲模态基本相同。

4.3 表2中屈曲临界荷载均比表1有所减少，经计算发现单层网壳在考虑几何非线性后屈曲临界荷载减少了2%，说明几何非线性对单层网壳失稳临界荷载有一定影响。

4.4 外界荷载的布置形式对单层网壳的失稳模态及临界荷载的影响有待进一步研究。