基于强跟踪无迹卡尔曼滤波的内置式永磁同步电机转子位置估计
马彦 李军伟 王琳 阚辉玉 孙宾宾 王冬


摘 要: 为了解决当永磁同步电机在运行中受到扰动、系统状态突变时,传统的无迹卡尔曼滤波算法对转子位置的跟踪能力下降、估计精度降低,甚至会使滤波器发散等问题,文中采用基于两相静止坐标系的内置式永磁同步电机数学模型的强跟踪无迹卡尔曼滤波算法,研究了在经典的无迹卡尔曼滤波的基础上引入强跟踪滤波器,既保留了经典的无迹卡尔曼滤波算法的优点,又能改善无迹卡尔曼滤波算法对状态突变鲁棒性的控制。仿真和实验结果表明,当永磁同步电机运行在中高速区域时,强跟踪无迹卡尔曼滤波算法可以快速准确地跟踪转子位置,估计误差低于经典的无迹卡尔曼滤波算法。
关键词: 电动汽车; 内置式永磁同步电机; 转子位置估计; 强跟踪滤波; 强跟踪无迹卡尔曼滤波; 实验验证
中图分类号: TN99?34; TM301.2 文献标识码: A 文章编号: 1004?373X(2020)13?0130?04
IPMSM′s rotor position estimation based on STUKF
MA Yan1, LI Junwei1, WANG Lin1, KAN Huiyu1, SUN Binbin1, WANG Dong2
(1. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China;
2. Beijing Qianqin Technology Co., Ltd., Beijing 100190, China)
Abstract: When the permanent magnet synchronous motor is disturbed during operation and the system is in a state of sudden change, the tracking ability and estimation accuracy of the conventional unscented Kalman filter (UKF) algorithm for the rotor position are reduced, and the filter is even diverged. For this reason, the STUKF (strong tracking UKF) algorithm which is based on the IPMSM(interior permanent magnet synchronous motor) mathematical model of two?phase stationary coordinate system is adopted. In the proposed algorithm, a strong tracking filter is introduced on the basis of the traditional UKF, which not only retains the advantages of the traditional UKF algorithm, but also improves the control method of the traditional UKF algorithm to the robustness of status sudden change. The simulation and experimental results show that when the permanent magnet synchronous motor runs at medium and high speed, the STUKF algorithm can track the rotor position quickly and accurately, and its estimation error is lower than that of the traditional UKF algorithm.
Keywords: electric vehicle; IPMSM; rotor position estimation; strong tracking filtering; STUKF; experimental verification
0 引 言
新能源汽车电机驱动系统中,内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor,IPMSM)因为有着更大的扭矩惯量比、更高的功率密度而被大规模使用[1]。在永磁同步电机磁场定向控制系统中,转子永磁体的电角度是坐标变换的基准,获取高精度的永磁体电角度有利于实现IPMSM的高性能矢量控制。
为了提高电驱动系统的稳定性、增强鲁棒性,可以不使用位置传感器而采用无传感器控制方案[2],常见的电机转子位置及转速估计算法主要有基于基波模型的扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法等[3?4]。EKF是线性的卡尔曼滤波(Kalman Filter,KF)在非线性域的延展,在非线性化程度不高的系统中有较好的效果[5],但实际上,EKF算法计算较复杂,并存在滤波器不稳定的情况。而无迹卡尔曼滤波(Unscented Kalman Filter,UKF)则巧妙借助无迹变换(Unscented Transformation,UT)来近似后验概率密度,不会用到Jacobian矩阵[6],估算误差小于EKF,在某些非线性系统中更有优势[7]。然而,新能源汽车上的电机往往运行在复杂的工况下,永磁同步电机在运行时容易受到擾动,此时系统状态突变,无论UKF还是EKF的估计效果都会变差,甚至会使滤波器发散[8]。为了解决EKF的不足,文献[9]提出了强跟踪滤波器(Strong Tracking Filter,STF)的概念,STF具有较好的鲁棒性、强大的跟踪能力和中等复杂性。文献[10]提出了基于强跟踪滤波的UKF算法,并通过仿真证明了基于STF的UKF在估计准确性、滤波器可靠性以及对突然改变的状态和大的滤波器启动误差的鲁棒性方面优于UKF。
将强跟踪无迹卡尔曼滤波(Strong Tracking Unscented Kalman Filter,STUKF)算法应用于IPMSM的转子永磁体位置估算,以改善算法对永磁同步电机转子位置的估计精度和跟踪能力,使系统在受到干扰时仍然可以快速准确地获取转子永磁体位置。
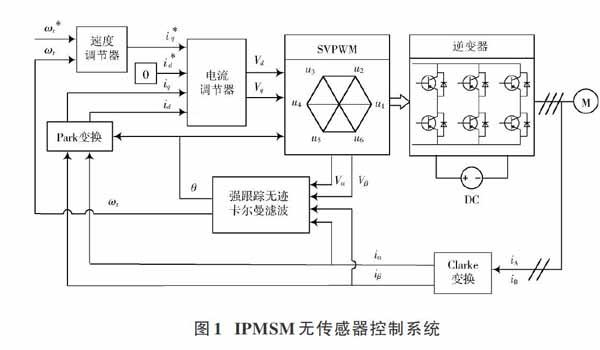
1 IPMSM无传感器磁场定向控制系统
通过分析IPMSM数学模型,明确了两相静止[αβ]坐标系模型[11]更有利于实现STUKF估计算法。IPMSM无传感器矢量系统如图1所示。通过在传统的无迹卡尔曼滤波观测器中引入强跟踪滤波器,借助强跟踪滤波的优势,尝试减少因系统干扰、状态突变而产生的估计误差,并保证良好的状态实时跟踪能力。
2 基于STUKF的转子位置估计算法
2.1 无迹卡尔曼滤波算法
无迹卡尔曼滤波是将无迹变换思想融合进卡尔曼滤波中,保证在非线性系统中应用KF算法时,不同于EKF中的线性化方法,采用确定性的抽样得到含有Sigma点估计值的协方差及均值[12]。将IPMSM的强跟踪无迹卡尔曼滤波估计算法离散化,得到如图2所示的Sigma点集及权值计算、时间更新和测量更新逻辑。
2.2 强跟踪无迹卡尔曼滤波算法
为了克服传统KF的不足,文献[13]引入了强跟踪卡尔曼滤波(Strong Tracking Kalman Filter,STKF)理论。
STKF有几个重要的优点,包括:
1) 对于模型不确定性有较好的鲁棒性;
2) 无论系统是否达到稳定状态,都有良好的实时状态跟踪能力;
3) 计算负荷适中。
将UKF和STF巧妙联系起来就有了STUKF。与STKF一样,次优渐消因子[14]被引入到所谓的STUKF中的非线性平滑算法中。时变滤波器增益矩阵中的次优渐消因子可按下式得到:
类似地,UKF算法中的协方差矩阵[Pzz]和[Pxz]也可以重写为:
3 转子永磁体位置估算的仿真
通过在Matlab/Simulink软件平台中仿真比较传统UKF算法和STUKF算法估计出的IPMSM转子永磁体的电角度,从而验证STUKF算法对IPMSM转子永磁体位置的估算精度。表1中展示了模型在环仿真使用的IPMSM模型数据。
通过对传统UKF和STUKF算法进行仿真,得到了如图3和图4所示的估算数据。
如图3所示,永磁电机转速在0~30 r/min时,由STUKF和传统的UKF算法估计的转速和永磁体位置都与实际值有很大差距,出现这种问题的原因在于:低速时,IPMSM反电动势信号的信噪比低,UKF算法和STUKF算法的输入信号的误差较大,因此估计精度低。如图4所示,当电机转速在2 000 r/min时,由STUKF估计出的IPMSM转速和永磁体位置与实际量的偏差更小。由仿真比较曲线得出:相比于传统的UKF算法,STUKF算法的估计误差更小,跟踪能力更强。
4 算法的实验验证
通过第3节的模型在环仿真,证明了在UKF算法中融合STF算法可以降低IPMSM永磁体位置的估計误差,提高跟踪能力,本节通过实验比较算法的估计误差。
在如图5所示的实验测试平台中,采用光编电机作为驱动电机,带动旋变电机旋转。采用Infineon Aurix TC275作为电机无感算法的运行平台,此单片机的峰值能力高达1 300 DMips,无需担心复杂估计算法的运算量。实际的转子永磁体位置由旋变专用芯片解析旋变正交差分信号得到。将传感器获取的实际量与估计算法得到的估算量通过CAN总线发送至上位机来实现精度对比。
图6和图7展示了电机起动和电机在中高速时的转速及转子位置实际值、传统UKF估计值和STUKF估计值。
如图6所示,电机运行在0~80 r/min时,基于STUKF和UKF估算的转速和转子永磁体位置都与实际值相差较大,但STUKF估计值误差相对较小,与仿真结果一致,是由电机低速运行时基波信号误差大所致。如图7所示,电机转速在3 600 r/min左右时,STUKF算法估算出的永磁体位置的稳定误差约为3.8°,小于传统UKF算法的估计误差。
对原始数据进行处理易得:STUKF算法估算出的永磁体位置的标准差是9.4°,误差的均值是5.3°,而传统UKF算法相应的值分别为11.7°和6.2°,STUKF算法的估计误差减小约1%。给定相同的目标转速及电机负载保证了实验数据的可靠性,通过定量分析得出STUKF算法估计出的永磁体位置的误差更小,跟踪性更好。
5 结 论
研究采用STUKF算法来估计新能源汽车电驱动系统IPMSM的转速及永磁体位置,通过融合强跟踪滤波算法,提高了系统对转子永磁体位置和转速的快速稳定跟踪能力。实验结果表明:对于IPMSM转子永磁体位置估算,STUKF算法比经典的UKF算法具有更小的估计误差,当系统受到扰动、状态突变时具有更强的跟踪能力。
注:本文通讯作者为李军伟。
参考文献
[1] LIU Tingting, TAN Yu, WU Gang, et al. Simulation of PMSM vector control system based on Matlab/Simulink [C]// 2009 International Conference on Measuring Technology and Mechatronics Automation. Hunan, China: IEEE, 2009: 343?346.
[2] 刘计龙,肖飞,沈洋,等.永磁同步电机无位置传感器控制技术研究综述[J].电工技术学报,2017,32(16):76?88.
[3] QIAO Zhaowei, SHI Tingna, WANG Yindong, et al. New sliding?mode observer for position sensorless control of permanent?magnet synchronous motor [J]. IEEE transactions on industrial electronics, 2013, 60(2): 710?719.
[4] 张洪帅,王平,韩邦成.基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J].中国电机工程学报,2014,34(12):1889?1896.
[5] 田红兵,樊光南,宋龙,等.基于EKF和PF的多机器人协同定位技术[J].现代电子技术,2013,36(23):95?98.
[6] 林辉,吕帅帅.基于双STF?UKF算法的永磁同步电机参数联合估计[J].东南大学学报(自然科学版),2016,46(1):49?54.
[7] ANTONOV S, FEHN A, KUGI A. Unscented Kalman filter for vehicle state estimation [J]. Vehicle system dynamics, 2011, 49(9): 1497?1520.
[8] JAFARZADEH S, LASCU C, FADALI M S. Square root unscented Kalman filters for state estimation of induction motor drives [J]. IEEE transactions on industry applications, 2013, 49(1): 92?99.
[9] ZHOU Donghua, XI Yugeng, ZHANG Zhongjun. Suboptimal fading extended Kalman filtering for nonlinear systems [J]. Control & decision, 1990, 5(5): 1?6.
[10] LI Zheng, PAN Pingjun, GAO Dongfeng, et al. An improved unscented Kalman filter based on STF for nonlinear systems [C]// 2009 2nd International Congress on Image and Signal Processing. Tianjin, China: IEEE, 2009: 1?5.
[11] 马彦,李军伟,李德芳,等.基于改进无迹卡尔曼滤波的内置式永磁同步电机转子位置估计[J].广西大学学报(自然科学版),2018,43(6):2154?2162.
[12] JULIER S J, UHLMANN J K, DURRANT?WHYTE H F. A new approach for filtering nonlinear systems [C]// Proceedings of 1995 American Control Conference. Seattle, WA, USA: IEEE, 1995: 1628?1632.
[13] ZHOU D H, FRANK P M. Strong tracking filtering of nonli?near time?varying stochastic systems with coloured noise: application to parameter estimation and empirical robustness analysis [J]. International journal of control, 1996, 65(2): 295?307.
[14] XIA Qijun, RAO Ming, YING Yiqun, et al. Adaptive fading Kalman filter with an application [J]. Automatica, 1994, 30(8): 1333?1338.

