玻璃纤维含量对加筋砂土边坡稳定性的影响研究

（江西理工大学 建筑与测绘工程学院，江西 赣州 34100）

0 引言

砂土是一种常见的建筑材料，在路基的填筑中被广泛使用，但由于其土体粘聚力较小，因此研究人员尝试将其与不同的加筋材料结合来增加其粘聚力，从而增大其整体的剪切强度。吴景海[1]选取5 种常见的土工合成材料作为砂土的加筋材料，通过三轴试验测得这5 种加筋土的剪切强度，进而分析比较了5 种材料的加筋效果。李丽华等[2]通过直剪试验，研究了含水量变化对纤维加筋土剪切强度的影响，结果表明含水量的变化主要引起纤维加筋土内摩擦角的变化。孙皓等[3]研究了纤维长度对加筋土强度的影响，结果表明纤维长度的变化几乎不会引起加筋土粘聚力的改变。孔玉侠等[4]研究了聚丙烯纤维材料的加筋效果，郑俊杰等[5]结合纤维和微生物钙化，进一步提高了加筋砂土的强度。本文在前人研究的基础上，基于大型直剪试验数据拟合得到不同玻璃纤维含量下加筋砂土剪切强度、粘聚力以及内摩擦角的函数表达式，进而通过算例分析了玻璃纤维含量变化给加筋砂土边坡稳定性带来的影响。

1 玻璃纤维含量对加筋砂土剪切强度的影响

1.1 试验方案

本文首先配置出四种不同玻璃纤维含量（0.1%、0.2%、0.4%以及0.6%）的加筋砂土，接着通过SHEARTRAC Ⅲ大型直剪仪来获得四种加筋砂土在不同竖向应力（45kPa、90kPa、135kPa 以及180kPa）下，剪切应力与剪切位移间的关系曲线。最后，根据上述关系曲线获得最大剪切应力即剪切强度与其对应的竖向应力，进而拟合得到两个剪切强度参数，即粘聚力和内摩擦角。

1.2 试验结果及分析

四种不同玻璃纤维含量（0.1%、0.2%、0.4%以及0.6%）下加筋砂土剪切强度与竖向应力之间的关系曲线如图1所示，该曲线通过对试验数据点进行拟合得到。四种不同玻璃纤维含量下，加筋砂土的剪切强度函数表达式、拟合曲线的决定系数R2以及由关系曲线拟合得到的两个剪切强度参数（粘聚力、内摩擦角）值列于表1。

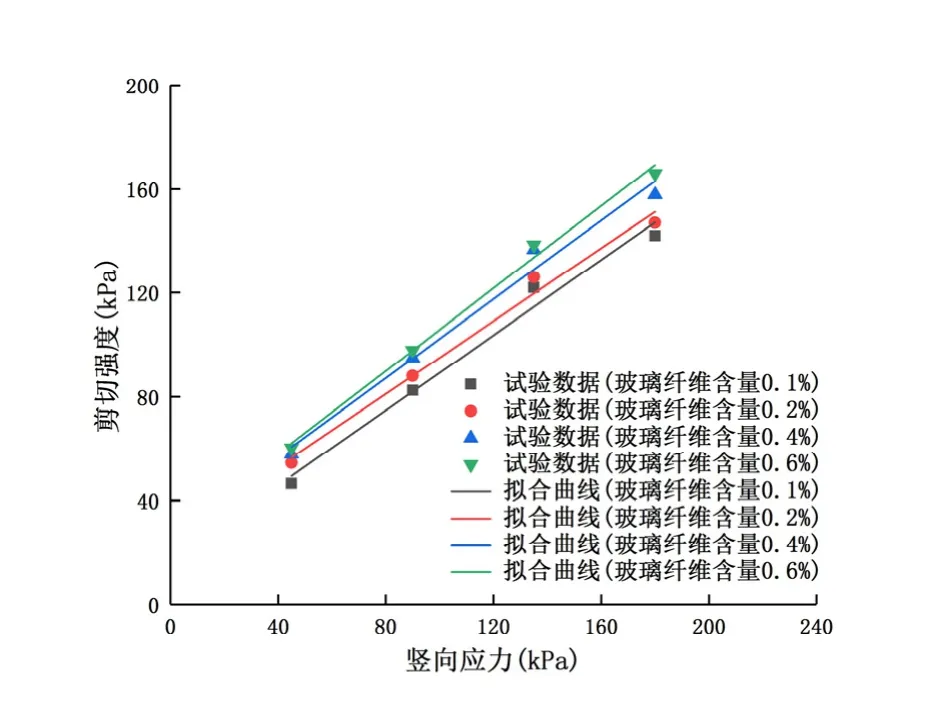
图1 不同玻璃纤维含量下加筋砂土剪切强度与竖向应力的关系曲线

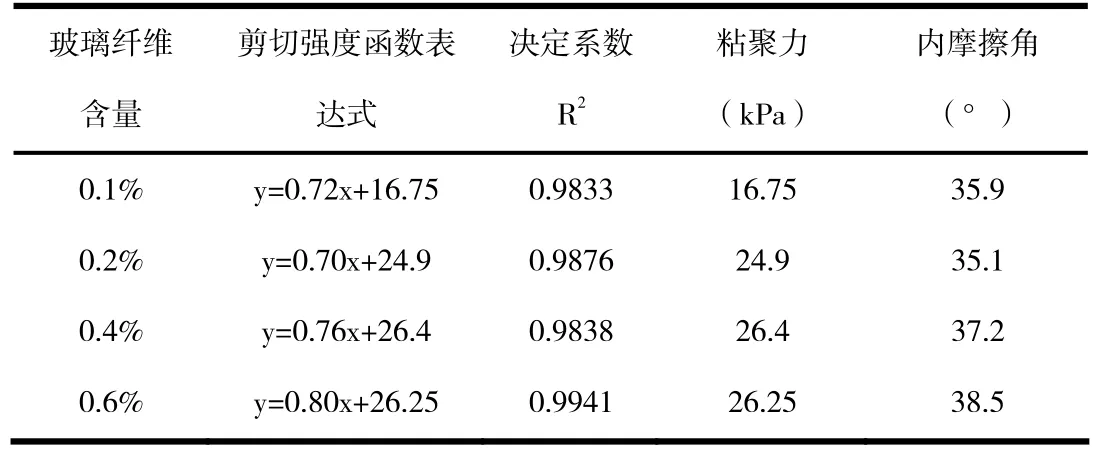
表1 不同玻璃纤维含量下加筋砂土剪切强度参数值

从图1可以看出，玻璃纤维含量越大，加筋砂土的剪切强度越大，这是由于玻璃纤维增大了砂土颗粒之间的摩擦力，玻璃纤维含量越大的加筋砂土，颗粒间的总摩擦力就越大，在相同的外力作用下，越不容易发生剪切变形。从表·1 可以发现，加筋砂土的粘聚力和内摩擦角都呈现上升的趋势，其中粘聚力的变化幅度为56.7%，内摩擦角的增加幅度为7.2%。因此，玻璃纤维含量变化给加筋砂土剪切强度带来的影响主要体现在粘聚力方面。

为了更好的预测出加筋砂土的粘聚力和内摩擦角与玻璃纤维含量之间的关系，利用一元二次多项式对表1中的数据进行拟合，具体的拟合关系式、拟合的决定系数R2和方差列于表2。

表2 玻璃纤维含量与粘聚力和内摩擦角之间的拟合关系式以及评价参数

从表2可以看出，决定系数接近1，方差小于1，因此拟合得到的玻璃纤维含量与加筋砂土粘聚力和内摩擦角之间的拟合关系式具有较好的拟合效果，可以应用到玻璃纤维加筋砂土边坡的稳定性计算中。结合表2，进一步可以发现，加筋砂土的粘聚力有着先快速增大后平缓下降的趋势。因此，基于表2中加筋砂土粘聚力与玻璃纤维含量之间的拟合关系式可以得到，当玻璃纤维含量为0.44%时，加筋砂土的粘聚力达到最大值。

2 玻璃纤维含量对加筋砂土边坡稳定性的影响

无论是自然边坡还是人工边坡，都会时常发生失稳破坏，因此用来分析这些边坡稳定性的计算方法是众多学者研究的重点。当前，边坡极限平衡法在实际工程中应用地最为广泛，该方法的基本原理是基于力的平衡以及力矩平衡，得到滑面上的法向力以及切向力分布，进而求解出滑面的安全系数。因此，该方法的优点在于其原理简单，方便应用，同时针对一些复杂的边坡以及外部因素（渗流、各种外部荷载）也能够很好地适用。极限平衡法经过众多学者的不断研究，使其能够适用的范围更广且基于的假设也越来越合理。目前考虑全局平衡的极限平衡法有Janbu 法、Spencer 法以及Morgenstern ＆ Price 法，通过对上述方法的比较发现，尽管它们对于条块之间力的假设不同，但由于满足全局平衡条件，得到的结果十分接近，这些方法计算出的安全系数最大差幅不超过5%。简化Bishop 法虽然不能够完全满足全局平衡的所有条件，但也给出了与考虑全局平衡方法十分接近的结果，由于结果的精确性以及计算过程更为简洁，由Bishop 提出的极限平衡条分法已被广泛用于分析预测土质边坡的稳定性。

为了研究玻璃纤维含量对加筋砂土边坡稳定性的影响，本文选取如图2所示的玻璃纤维加筋砂土边坡算例，坡长为24.4m，坡高为12.2m，O 为原点，X 轴正方向指向坡内，Y 轴正方向竖直向上，算例中的计算滑面为圆弧形，其圆心为F(6.1,21.3)，半径为24.4m。该加筋砂土边坡的重度为14.9kN/m3，粘聚力和内摩擦角通过将玻璃纤维含量数值代入表2中的两个拟合关系式得到。分别利用简化Bishop 法和简化Janbu 法计算算例边坡滑面在不同玻璃纤维含量下的安全系数，具体计算结果列于表3。

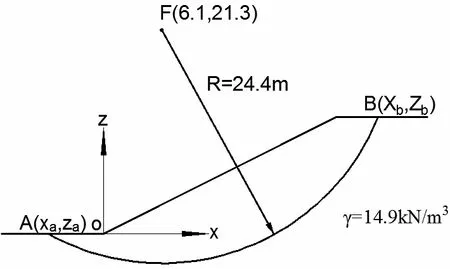
图2 玻璃纤维加筋砂土算例边坡

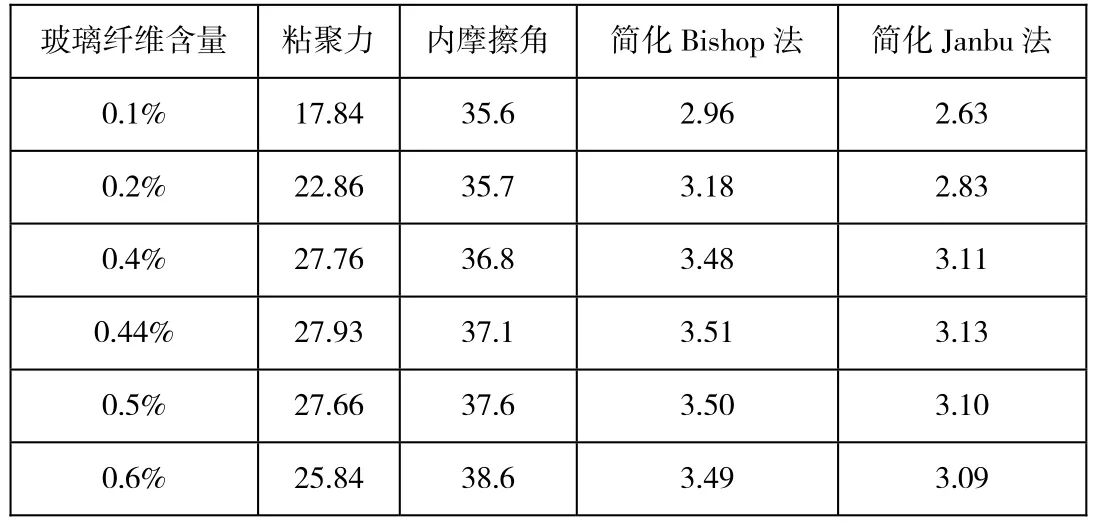
表3 不同玻璃纤维含量下算例边坡滑面的安全系数

从表3可以看出，简化Bishop 法和简化Janbu 法得到的结果十分接近。随着玻璃纤维含量的增大，加筋砂土边坡的安全系数先是逐渐提高，然后平缓下降，这是由于玻璃纤维含量的变化主要引起加筋砂土粘聚力的变化，并且其粘聚力也呈现上述趋势。当玻璃纤维含量为0.44%时，边坡的安全系数达到最大值，因此0.44%为玻璃纤维加筋砂土边坡中最佳的玻璃纤维含量。

3 结论

（1）通过大型直剪试验得到四种不同玻璃纤维含量（0.1%、0.2%、0.4%以及0.6%）下加筋砂土剪切强度及其对应的竖向应力，通过对这些试验数据点进行拟合得到不同玻璃纤维含量下加筋砂土的剪切强度函数表达式，进而得到粘聚力和内摩擦角，其中粘聚力的变化最为明显。

（2）利用一元二次多项式对四种玻璃纤维含量下加筋砂土的粘聚力和内摩擦角进行拟合，得到可以计算不同玻璃纤维含量下加筋砂土粘聚力和内摩擦角的计算关系式，该关系式具有较好的适用性。

（3）通过算例，基于简化Bishop 法和简化Janbu 法分析了不同玻璃纤维含量下加筋砂土边坡安全系数的变化。结果表明，随着玻璃纤维含量的增大，加筋砂土边坡的安全系数先是逐渐提高，然后平缓下降，当玻璃纤维含量为0.44%时，边坡的安全系数达到最大值。