增湿-冻融劣化原状黄土的结构强度模型
折海成, 胡再强, 王 凯, 梁志超, 冯 哲, 郭 婧
(1.西安理工大学岩土工程研究所,西安 710048;2.水利部土石坝破坏机理与防控技术重点实验室,南京 210024;3.榆林学院建筑工程学院,榆林 719000)
黄土显著的结构性是黄土特殊的物理力学性质的主要原因,也是黄土严重致灾性的重要根源,如黄土滑坡、崩塌、湿陷性、地面塌陷、地裂和不稳定边坡等。岩土工程问题的研究核心就是在复杂外界环境和力学扰动作用下土体的变形、强度和稳定性分析。黄土边坡和设施受到外界环境(包括地下和雨水入渗、温度等)的扰动作用导致黄土微结构联结和排列方式的变化,改变了黄土物理性质,劣化了黄土结构强度。笔者前期通过试验方法研究了增湿-冻融作用对黄土结构强度劣化规律[1]。为了方便评价工程设计合理性和现场施工安全性,需建立黄土结构强度损伤模型具有良好实用价值。
近年来,大量学者将强度统计理论应用在损伤力学中建立了许多不同材料的统计损伤模型、统计本构模型。朱振南等[2]假定受热损伤的岩石微元强度服从Normal分布,引入热损伤变量考察了岩石统计热损伤本构模型;田振元等[3]假设岩石微元强度服从Weibull随机分布,根据损伤力学理论的 Lemaitre应变等价性原理,在微元强度度量方法上考虑损伤阀值的影响,并结合Lade-Duncan强度破坏准则,建立了统计损伤本构模型;郑志等[4]在文献[3]假设的基础上,引进Mogi-Coulomb准则建立了岩石压缩破坏过程中损伤变量及统计损伤本构模型。龙尧等[5]考虑了土-结构接触面剪切特性,基于统计损伤理论提出了土-结构接触面剪切损伤模型及模型参数的确定方法;张慧梅等[6]考察岩石内部裂隙和孔隙分布的随机性,运用连续损伤力学理论,建立了围压与轴压共同作用下岩石的统计损伤模型;邓华锋等[7]基于连续损伤力学和统计理论,对三轴压缩试验应力-应变曲线特点进行分析,探讨了水岩作用对中砂岩劣化损伤机理,并建立了损伤统计本构模型。罗晓辉等[8-9]采用破坏统计理论研究结构性土体的损伤特性,提出了关于Weibull分布的土体强度分析方法,并得到了结构性土体的宏观损伤演化方程和本构模型;曹文贵等[10]研究了岩石蠕变过程统计损伤模型及模型参数的确定方法;汪辉平等[11]在相关假定基础上,引入统计损伤理论建立了能够考察应变软化类岩石受力变形全过程的统计损伤本构模型;赖远明等[12]、Yang等[13]研究了高温冻结黏土单轴随机损伤本构模型和强度分布规律、以及分析了富冰砂岩蠕变统计学特性;张德等[14]通过假设微元强度服从Weibull随机分布,并根据统计学和连续损伤力学理论建立能反映冻土破损全过程的损伤本构模型;Mu等[15]基于损伤力学理论,重新定义了节理岩体损伤变量,并建立了可评价冻融循环的统计损伤模型,可以较好地反映了循环冻融条件下节理岩体剪切强度的降解特性;Zhang等[16]基于连续破坏力学理论,建立了模拟冻融循环和荷载作用下的岩石损伤模型,并推导得出一条冻融循环和载荷作用下岩石的微损伤和诱发材料力学性能的损伤演化曲线,该曲线可以反映内部微裂纹的闭合,起始,传播和合并以及随后出现宏观裂纹和岩石破裂。
将强度统计理论应用在损伤力学中建立考察增湿、冻融及二者耦合作用下的黄土结构强度统计损伤模型,是研究的核心和创新点。首先,通过侧限压缩曲线定义黄土结构强度、剩余结构强度和损伤变量,并从深层机理上阐述采用损伤变量可表征黄土结构强度的劣化特性;其次,基于强度统计理论和损伤力学理论建立考虑增湿和冻融循环作用下的黄土结构强度统计损伤模型,基于试验数据对模型参数进行确定;最后,取其他基坑原状黄土,测定该模型所需变量,获得损伤试验值与损伤模型进行验证。
1 黄土结构强度劣化表征
黄土结构强弱可用结构强度大小表示,黄土结构强度是土结构在生成过程中形成的一种胶结性的联结强度,其伴随土体结构的生成而生成,随土体结构的破坏而消失。微观力学机理认为其大小由黄土颗粒之间的联结结构强度和摩擦结构强度所决定。黄土结构强度可以根据侧限压缩试验中压力p和孔隙比e关系曲线,即e-lgp曲线定义。笔者认为原状黄土在侧限压缩试验加荷过程中,e-lgp压缩曲线可以表征黄土结构从平缓直线阶段的弹性变形到由局部微观结构开始破坏而使线段曲率突增进入塑性变形,则定义曲率最大点处对应的压力为试验原状黄土结构强度。为了追究取样制样过程对原状黄土结构强度的影响,采用先期固结压力所对应的点与该点处孔隙比对应饱和重塑黄土的压力差表示原状黄土结构强度更为合理,定义为原状黄土结构强度q0,如图1所示。

直线①为压缩曲线的末段直线方程;直线②为过最大曲率点的切线方程;直线③为过最大曲率点的水平直线;直线④为直线②和③角平分线;Rmin为最小曲率半径图1 原状黄土的结构强度Fig.1 Structural strength of undisturbed loess
则原状黄土的结构强度可表示为
q0=pc-ps
(1)
式(1)中:pc为先期固结压力,kPa。先期固结压力最常采用卡莎格兰德方法确定,该方法需要严格进行试验操作和数据读取,以便提高精度。
而对于受到外界环境(增湿、温度变化、加荷等)扰动作用黄土的结构强度,采用压缩曲线有明显的转折点,该点也认为是黄土微观结构的破坏起点,该点处孔隙比所对应的外界环境扰动黄土与饱和重塑黄土的压力差最大,此数值定义为黄土剩余结构强度qr,如图2所示。

图2 扰动黄土的剩余结构强度Fig.2 Residual structural strength of disturbed loess
则扰动黄土剩余结构强度可表示为
qr=pcmax-ps
(2)
当前,损伤力学又新发展一个损伤与愈合力学支派,其研究理论是材料在外界扰动和其结构内部改变过程中,可能会出现微空洞、孔隙和裂缝的扩展、贯穿并汇合等微缺陷演化向使劣化方向发展的损伤过程;同时,也会在微扰动和蠕变过程中,可能出现这些微空洞、孔隙和裂缝的闭合并相互嵌入等微缺陷演化向使愈合方向发展。则传统损伤力学是损伤和愈合迭加,其实质是材料损伤和愈合的有效损伤。考虑增湿和冻融作用都是使黄土体积膨胀,对黄土结构强度均有较强的劣化影响。增湿过程是水分富集在孔洞和裂缝中,在荷载作用下,富集水像“水楔子”使内部空洞、孔隙和裂缝的扩展、贯穿并汇合而改变黄土微缺陷的构型;水土作用会导致黄土微颗粒或微颗粒集合体之间胶结物质的联结力降低;水的润滑特性使得微颗粒或微颗粒集合体之间的摩擦也大大降低,进而降低了黄土的结构强度。在水分对黄土强度劣化的基础上,赋存于微孔隙中的水分由于冻融产生不均匀的运移与分布,同时水分的相态变化,改变水分的体积,进而产生冻胀,使得黄土内部空洞、孔隙和裂缝等微缺陷构型与联结方式再次发生改变,结构强度进一步受到劣化和降减。综合上述分析,增湿和冻融作用产生作用使黄土结构强度向损伤发展明显强于向愈合发展,愈合可忽略。采用传统损伤力学的损伤变量来表征黄土结构强度劣化是可行的,并具有较强的理论依据。
根据损伤力学理论,定义损伤变量为
(3)
一般情况下,Ω取值在0~1。当Ω=0时,表明没有受到任何扰动损伤;当Ω=1时,表明充分扰动损伤,即饱和重塑状态。
当qr为取图1中曲率最大点对应的pcmax计算的剩余结构强度,用q0r表示取样制样扰动后剩余结构强度,则式(3)变化为
(4)
式(4)中:Ωd表示黄土在开挖后上覆压力释放和取样制样过程对黄土产生不同程度的扰动,其值越大表示扰动越大。
Ωd可以根据图1、式(4)进行求解,求解过程参阅文献[1],以得到原状黄土的结构强度q0、剩余结构强度qr和取样制样扰动损伤变量Ωd计算公式如式(5)~式(7)所示:
(5)
qr=10lgpcmax-(lgpcmax)s=
(6)
Ωd=1-
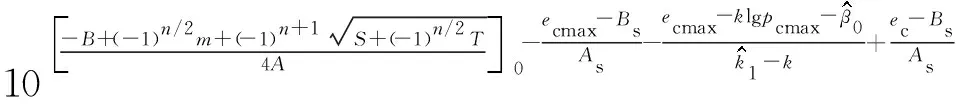
(7)
经计算得到原状黄土的结构强度q0=1 035.18 kPa,取样制样扰动损伤变量Ωd=0.177。
2 黄土统计损伤模型建立
2.1 黄土损伤模型构建思路
黄土微结构认为是由黄土微颗粒或微颗粒集合体及它们之间几何排列和胶结等综合表征,其内含有大量随机空洞、孔隙和裂缝等缺陷,为了使黄土保持原始基本单元结构形式不被破坏的能力,黄土具有一定的结构强度这一特殊力学性质。在外环境扰动和荷载下,黄土微结构胶结和微缺陷构型被劣化及土骨架颗粒产生变形破坏,假定黄土微结构是由不同土颗粒或微颗粒集合等微单元组成的,其微单元强度服从Weibull分布的特点,结合 Lemaitre[17]提出的应变等价性假设,引用统计理论方法研究增湿和冻融作用引起黄土微观损伤具有较好的效果。
Krajcinovic等[18]应用连续损伤理论和强度统计理论相结合提出统计损伤模型,如式(8)所示:
(8)
式(8)中:E为弹性模量;ε为应变;Ni为第i种作用下失效的微单元数;N为微单元的总数。
综上所述,在取样制样扰动过程中的黄土结构强度为取样制样扰动时的黄土剩余结构强度q0r;以吸水增湿后,冻融循环前的黄土结构强度为增湿损伤状态时的黄土剩余结构强度qwr;以冻融循环后的黄土结构强度为冻胀损伤状态时的黄土剩余结构强度qnr。根据损伤力学理论,建立了黄土结构强度损伤的基本方程:
q0r=q0(1-Ωd)
(9)
qwr=q0(1-Ωd-Ωw)
(10)
qnr=q0(1-Ωd-Ωw-Ωn)
(11)
式中:Ωw为增湿后的水化损伤变量;Ωn为冻融循环后冻胀损伤变量。
2.2 黄土统计损伤模型建立
用Weibull分布能很好地分析微细观损伤,即损伤概率密度函数P(η)可以表达为
(12)
式(12)中:β为形状参数;F0为尺度参数;η为膨胀率。
将式(9)~式(11)与式(8)分别进行分析,可以定义随机损伤变量为Ni和N的比值,单因素损伤变量分为取样制样扰动损伤变量、吸水增湿后随机损伤变量和冻胀后随机损伤变量三部分。并进一步假设每一种体积膨胀率分别达到某一水平ηd、ηw和ηn时,其损伤的单元数目为N(ηd)、N(ηw)和N(ηn)。
(13)
(14)
(15)
为了探索黄土在原始地应力下的应力和结构分布状态,根据图1,可推演出黄土试样回归在先期固结压力下的体积与压力释放后的体积之间关系如式(16)所示:
(16)
式(16)中:e0为初始孔隙比;ec为先期固结压力下的孔隙比;Vd为先期固结压力下的体积,cm3;ΔVd为先期固结压力释放后的体积增量,cm3;V为试样体积,cm3。
由图1试验数据计算可知,e0=0.92,pc=1 035.18 kPa,ec=0.834。将这些数据代入式(16)得ΔVd=5.375 cm3。因此,试样体积可以近似在先前固结压力下减小到如式(17)所示的体积:
Vc=V-ΔVd=(120-5.375)cm3=114.625 cm3
(17)
因此,采样过程地层压力释放后产生的膨胀率为
(18)
将增湿后的黄土体积变化回归在先前固结压力下的体积变化率如图3所示。
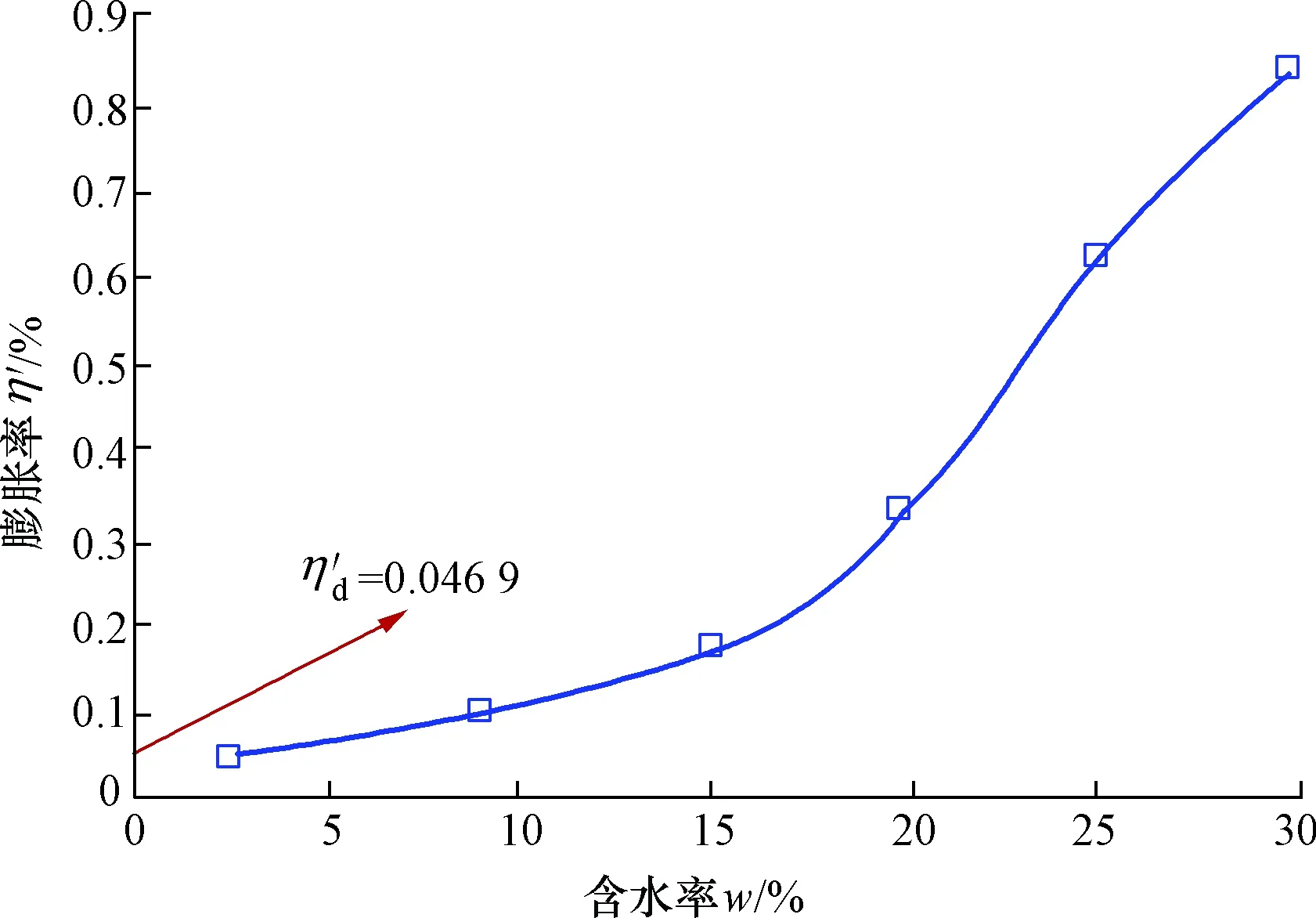
图3 增湿后体积的变化规律Fig.3 Volume changing after moistening
类似地,将增湿和冻融循环后黄土试验膨胀率也如上方法近似回归在先期固结压力的情况下。由式(17)、式(18)可得
(19)
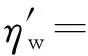
(20)
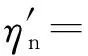
(21)
(22)
同样,将冻融循环后的体积变化回归在先前固结压力下的体积变化率如图4所示。

(23)
(24)
(25)
将式(12)代入式(23)~式(25)得
(26)
(27)
(28)
式中:Fn0和βn为冻融循环扰动损伤模型参数。
基于损伤力学的不可逆和叠加原理,在增湿和冻融作用下原状黄土结构强度损伤变量可定义为
(29)
以体积膨胀率作为考考察变量,从图3可知,随含水率增加黄土体积膨胀率起初一段,增长缓慢,之后增长加快,为了提高精度拟合为两段直线,如表1所示。

表1 增湿作用下黄土膨胀率拟合公式Table 1 Fitting formula for loess expansion rate by moistening
(30)
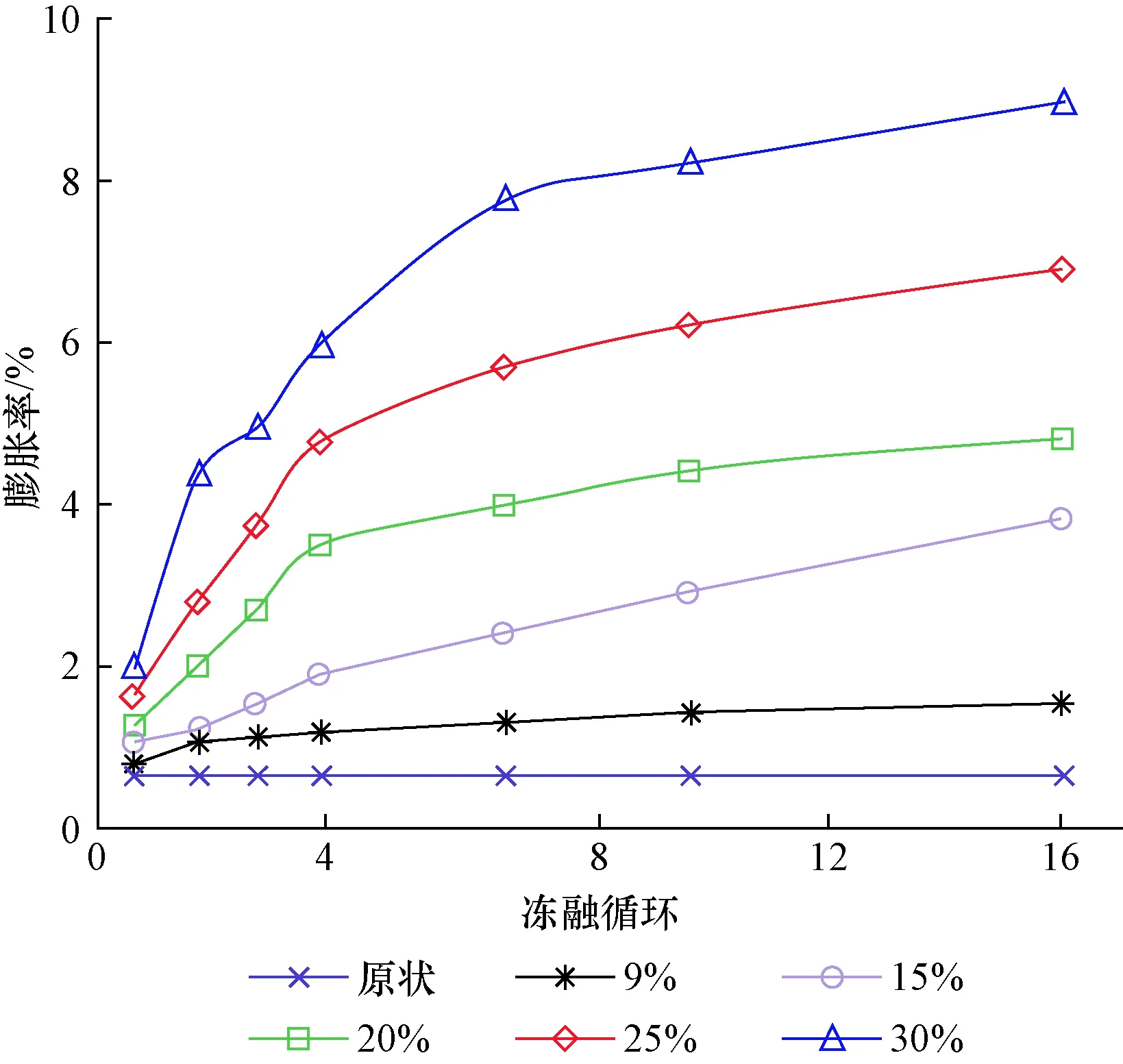
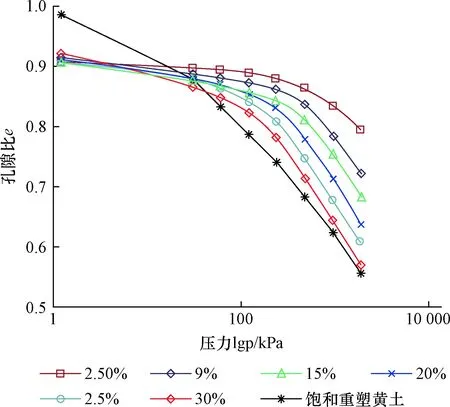
式(30)中:a1、a2、b1、b2为试验拟合系数,a1 从图4可知,原状黄土试样(含水率为2.5%),不随冻融循环次数增加改变黄土的体积,说明冻融循环对黄土结构强度没有损伤;在其他含水率下,随冻融循环次数增加黄土体积膨胀率起初一段,增长较快,之后增长减缓,为了提高精度拟合两段直线,如表2所示。 表2 冻融循环作用下黄土膨胀率拟合公式Table 2 Fitting formula for loess expansion rate by freezing-thawing cycles (31) 式(31)中:c1、c2、d1、d2为试验拟合系数,可通过试验数据计算得到,c1>c2。 将函数f(w)和f(n)代入式(12)和式(29),得增湿和冻融循环损伤概率密度函数,增湿水土作用和增湿-冻融循环耦合作用的损伤变量。 在增湿过程中,损伤概率密度函数表示为 (32) 式(32)中:i=1或2,由式(30)确定。 在不同含水率下,随冻融循环次数增加的损伤概率密度函数表示为 (33) 式(33)中:i=1或2,由式(31)确定。 增湿水土作用和增湿-冻融循环耦合作用的损伤变量为 (34) 式(34)对相应的自变量进行求一阶导数,得增湿损伤演化函数g(w)和冻融循环损伤演化函数g(n): (35) (36) 将式(34)代入到式(9)~式(11)得增湿水土作用和增湿-冻融循环耦合作用下黄土结构强度统计损伤的基本方程: (37) (38) 将式(37)和式(38)进行简单移项整理,整理后对方程两边取对数可得: (39) (40) 将增湿过程中和在不同含水率下,冻融循环过程中的试验所得数据分别代入式(39)、式(40),计算出βw、βn、Fw0和Fn0的数值。 将表3模型参数代入式(34)可得黄土结构强度吸水增湿水化损伤模型: 表3 模型参数Table 3 Model parameteres (41) 将表3模型参数代入式(34)可得黄土结构强度增湿-冻融循环耦合作用的损伤模型,损伤变量记作Ωw,n。 当w≤wp时: (42) 当w>wp时: (43) 取西安北郊某基坑Q3黄土,埋深约为13 m左右。其基本参数如表3所示。 表3 黄土基本参数Table 3 Essential parameter of loess 采用文献[1]的试验方法,将黄土进行吸水增湿和不同次数冻融循环作用后进行测试,得到黄土体积膨胀率规律如图5、图6所示,通过侧限压缩试验得到黄土的e-lgp压缩曲线,如图7、图8所示。 图5 增湿体积变化规律Fig.5 Volume change after moistening 图6 冻融循环体积变化规律Fig.6 Volume change after freezing and thawing cycles 图7 原状黄土增湿后e-lgp曲线Fig.7 Undisturbed loess e-lgp curve after moistening 图8 不同含水率下黄土冻融循环后e-lgp曲线Fig.8 Loess e-lgp curve after freezing-thawing cycles in different water content 同样,以体积膨胀率作为考察变量,利用上述计算方法获得统计损伤模型参数和损伤变量的演化规律曲线,与试验测定的黄土损伤变量数值进行比较如图9、图10所示,也可以对损伤模型进行验证。 图10 黄土冻融循环损伤模型验证Fig.10 Validation of loess moistening freezing-thawing cycle damage model 从式(41)、图9可知,吸水增湿水化模型曲线:在w≤wp时,模型预测损伤变量值与试验值较为吻合;在w>wp时,模型预测损伤变量值较试验值偏低,所以在具体工程需加以验证和简单修正。 从式(42)、式(43)和图10可知,增湿-冻融循环耦合模型曲线:为了提高模型精度,依据含水率和冻融循环次数细化了分段条件,在w≤wp时,随冻融循环次数增加模型预测损伤变量值较试验值基本吻合,个别含水率下模型预测损伤变量值较试验值偏低;在w>wp时,当冻融循环次数n≤3,模型预测损伤变量值与试验值比较吻合;当冻融循环次数n>3,模型预测损伤变量值较试验值偏高,在工程设计较保守,具有安全性。 式(37)、式(38)分别可表示增湿和增湿-冻融循环耦合作用下的黄土结构强度劣化程度。 (1)依据压缩曲线定义黄土结构强度、剩余结构强度和损伤变量,并从深层机理上阐述了可以采用传统损伤变量来表征黄土结构强度在增湿和冻融作用下的劣化过程。 (2)基于微单元强度服从Weibull分布和 Lemaitre提出的应变等价性假设思路,建立了黄土吸水增湿和增湿-冻融耦合作用下的统计损伤模型,并在试验的基础上,确定出了损伤模型参数。 (3)对损伤变量进行求解出增湿损伤演化函数和冻融循环损伤演化函数,并将损伤变量代入损伤基本方程得出黄土结构强度增湿水土作用下和增湿-冻融循环耦合作用下的统计损伤基本方程。 (4)取西安北郊某基坑黄土对统计损伤模型进行验证,经讨论模型预测损伤变量值与试验值较吻合。
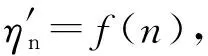
3 模型参数确定

4 实例分析与模型验证
4.1 实例概况及试验结果



4.2 模型验证

4.3 讨论
5 结论

