航空器跟随滑行动态冲突风险计算模型
康 瑞, 杨 凯
(1.中国民用航空飞行学院空中交通管理学院,广汉 618307;2.四川大学视觉合成图形图像技术国防重点学科实验室,成都 610064;3.四川大学计算机学院,成都 610064)
滑行是指航空器以自身动力在滑行道系统中的运动过程[1]。滑行阶段是机场场面运行主要组成部分。随着中国民航飞行量逐渐增加,部分枢纽机场的平均滑行时间超过25 min,航空器滑行安全与效率决定了机场场面运行水平,因此判断及量化滑行冲突成为民航业关注的重点课题。
中外相关学者对此展开了深入研究[2-9]。2010年,朱新平等[2]以增强型地面控制与引导系统(advanced surface guidance and control systems,A-SMGCS)为核心,对航空器资源占用冲突提出了解决方法;2013年,牟奇锋等[3]计算扩展航空器轮廓最小间隔,提出了滑行碰撞概率评估方法;2015年,冯兴杰等[4]以避让冲突交叉口为目标,构造了多蚁群协同进化的滑行道优化分配算法;2016年,潘卫军等[5]考虑机身与翼展范围,针对十字交叉口的相遇滑行过程,设计了碰撞风险评估算法;2017年,夏正洪等[6]提取航空器的滑行轨迹,利用实时位置计算间隔并判断冲突;2018年,张天慈等[7]建立混合整数规划模型进行仿真了阻塞、冲突等扰动下的场面运行恢复过程;董兵[8]将滑行冲突点定位于滑行道交叉口建立了冲突避让模型;2019年,张兆宁等[9]提出的远端绕行滑行路径优化模型中,以航空器占用共用节点时间差小于滑行安全间隔定义滑行冲突。目前相关研究主要存在的问题有:①对交叉滑行冲突研究较多,对跟随滑行冲突研究很少;②传统方法均以推测两架航空器到达最接近共用资源的时机、位置判断冲突,由于跟随滑行时两航空器已位于共用资源(同一条滑行道)中,因此无法将现有方法直接应用于跟随滑行中。而在实际管制过程中,在低能见度条件下,管制员、后机机长无法目视判断间隔,容易形成追赶,造成危险接近,甚至产生碰撞。这种情况下,塔台管制员应根据场面监视数据[10]判断冲突趋势,及时发布指令调整间隔。实际上为降低对恶劣天气影响,越来越多的大中型机场实施低能见度下运行程序[11],由此引入场面监视数据,针对航空器跟随滑行过程,定义跟随冲突标准,量化冲突概率,构造实时动态冲突计算模型,为飞行员提供跟随冲突告警预警,对保障机场运行安全有重要意义。
为此,在满足相关管制规定的基础上,抽象跟随滑行过程,考虑喷流范围、机身长度等关键要素,建立航空器跟随滑行动态冲突计算模型。采用 Visual C++平台实现模型并进行仿真计算,分析关键参数对动态冲突的影响,并利用实时真实轨迹对本文模型进行验证。
1 问题提出
设fi、fj为同向滑行的两架航空器,如图1所示,两机依次在滑行道Tn上由右至左滑行,fi距离滑行道末端更近为前机,fj位于fi后方为后机。li、lj为机身长度。两航空器所处的深灰色区域为共用滑行道。fi后方长度为ΔSi,j的浅灰色区域为两机之间最小纵向间隔,该间隔由管制规则、前后机尾流等级差异综合决定。

图1 航空器跟随滑行冲突Fig.1 Conflict of aircraft successively taxiing
假设fi到达Tn末端后左转进入下游滑行道,此后离开共用滑行道并与后机fj成分散态势。设fi、fj在t时刻滑行速度分布为vi(t)、vj(t),fi、fj与滑行道Tn末端距离为Si(t)、Sj(t),fi、fj纵向间隔为
ΔGi,j(t)≈Sj(t)-Si(t)-li
(1)
设fi、fj纵向间隔为ΔSi,j,若跟随滑行中的某时刻t,两机之间距离小于安全间隔ΔSi,j,则两机冲突:
ΔGi,j(t)<ΔSi,j
(2)
将满足式(2)的情况定义为事件C(t),根据速度、位置定义并求解P[C(t)]即可计算动态冲突概率。
2 航空器跟随滑行冲突计算模型
2.1 模型建立
定义TOi,n(t)为以t时刻fi速度位置,推算得到的fi离开Tn,全机身进入下游滑行道的滑行时间:
(3)
小于安全间隔是指水平距离小于ΔSi,j的情况,设冲突时的最大间隔为ΔSi,j-1。令TCj,n(t)为以t时刻fj速度位置,推算得到fj到达距离Tn末端小于安全间隔,即形成冲突的所需滑行时间:
(4)
若在Tn内,fj追赶fi并形成冲突,应满足:
∃t, TOi,n(t)≥TCj,n(t)
(5)
因此可将t时刻冲突风险概率描述为
P[C(t)]=P[TOi,n(t)≥TCj,n(t)]
(6)
可将式(6)改写为
(7)
将式(7)改写为函数形式:
(8)
由此式(7)可表示为
P[C(t)]=P{f[vi(t),vj(t)]≥0}
(9)
定义vmax为最大滑行速度,vTmax为最大转弯速度,Δv为每秒钟速平均加速度,设航空器fi的预测滑行速度值域为
(10)
(11)
由此可得,两航空器顺向跟随滑行冲突风险为
(12)
2.2 模型求解
设下一时刻fi速度在速度值域范围内呈均匀分布,可得vi(t)的概率密度函数φ[vi(t)]为
(13)
同理可得fj速度vi(t)的概率密度函数:
(14)
图2给出vi(t)、vi(t)取值及f[vi(t),vi(t)]的线性表示,满足式(7)、式(8)条件的f[vi(t),vi(t)]值域范围用阴影表示,设该阴影范围面积为D(t)。
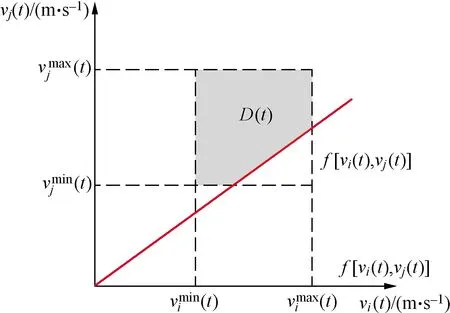
图2 冲突时的速度范围Fig.2 Speed range in conflict
由图2可得:


(15)
将式(13)、式(14)代入式(15),可得每时刻动态跟随冲突概率,同时为满足0≤P[C(t)]≤1,令:
P[C(t)]=max(0,min{1,P[C(t)]})
(16)
3 程序设计及数据分析
3.1 冲突概率计算程序设计
设机场飞行区为4E级[12],长度为1 500 m的平行滑行道上,有两架航空器同向跟随滑行。根据机场管制规则[1],令vmax=13.8 m/s,vTmax=4 m/s,Δv=1.0 m/s[13-14],设fi、fj为常见的尾流中型运输机,li=lj=45 m,ΔSi,j=50 m。利用VC++编程,建立机场跑道、滑行道结构,并动态仿真航空器跟随滑行过程。图3分别给出两机由于速度、位置差异造成的不同跟随滑行状态。图3(a)描述了前、后机以相同速度保持间隔滑行过程,图3(b)描述了后机追赶前机,小于安全间隔造成冲突过程,图3(c)描述了后机速度减慢,与前机间隔增大的情况。

图3 动态仿真运行示意图Fig.3 Schematic diagram of dynamic simulation operation
3.2 仿真模拟及数据分析
在动态滑行仿真基础上,以图4中给出的程序结构及逻辑,对匀速、匀加速、匀减速运动下动态冲突进行计算。初始设置前机fi距离滑行道末端500 m,即Si(0)=500 m,定义ΔGi,j(0)为初始时刻两航空器水平间隔。设ΔGi,j(0)为50~250 m,t为1~100 s,每次仿真令t增加1 s,令ΔGi,j(0)增加2 m。即可得到随时间t、ΔGi,j(0)动态变化冲突风险。

图4 滑行冲突计算结构 Fig.4 Taxiing conflict calculation structure
3.2.1 匀速运动时的冲突风险计算
设fi、fj进行5 m/s的匀速、等距离运动,图5给出冲突风险P[C(t)]变化情况。

图5 匀速运动时冲突风险变化趋势Fig.5 The tendency of conflict risk in uniform motion
如图5所示,匀速运动时冲突风险P[C(t)]与ΔGi,j(0)取值成负相关,当ΔGi,j(0)>94冲突风险与t成负相关,50≤ΔGi,j(0)≤94,冲突风险与t成正相关。这是由于两机匀速运动,ΔGi,j(0)越大,后机追赶前机可能性越低,冲突风险越小。当ΔGi,j(0)>94,随着t增加,前机逐渐接近滑行道末端,虽然前机转出时会减速至4 m/s,与后机产生速度差,但由于两机距离较大,较小速度差无法造成追赶冲突,因此P[C(t)]随t增加逐渐减少,最大值为0.5。而50≤ΔGi,j(0)≤94时,两机距离较近,短时间的追赶即会形成冲突,因此P[C(t)]随t增加而增大,当ΔGi,j(0)<78,前机转弯时TOi,n(t)增加,而TCj,n(t)减少,满足式(3)冲突条件,因此P[C(t)]最大值为1.0。
3.2.2 匀加速运动时冲突风险计算
设fi以5 m/s匀速运动,fj以0.1 m/s2[15]静止开始做匀加速运动,图6给出冲突风险变化情况。
如图6所示,匀加速运动时,ΔGi,j(0)≥180,P[C(t)]恒为0。这是由于后机是从静止逐渐加速的,由于前机为5 m/s匀速运动,t在1~50 s呈前快后慢趋势,t在51~100 s呈前慢后快趋势,若初始间隔较大,后机追赶前机所需时间TCj,n(t)较长,因此在前机离开滑行道时仍能满足安全间隔,冲突风险很小。当ΔGi,j(0)<180,P[C(t)]与t正相关,与ΔGi,j(0)负相关,说明初始间隔越小,后机速度越大,追赶趋势越明显,越容易造成冲突。当ΔGi,j(0)<110,P[C(t)]最大值为1.0,且ΔGi,j(0)越小,P[C(t)]=1.0对应的时间范围越长,ΔGi,j(0)=50时,P[C(t)]=1.0对应时间区间为83~100 s,表明按照当前速度,后机会在83 s追上前机并小于安全间隔,需在83 s前采取减速措施,避免冲突。

图6 匀加速运动时冲突风险变化趋势Fig.6 The tendency of conflict risk in uniformly accelerated motion
3.2.3 匀减速运动时冲突风险计算
设fi以5 m/s匀速滑行,fj初始10 m/s并以-0.1 m/s2匀减速至静止,图7为冲突风险变化。

图7 匀减速运动时冲突概率变化趋势Fig.7 The tendency of conflict risk in uniformly deceleration motion
如图7所示,P[C(t)]与ΔGi,j(0)、t均负相关。这是由于后机是从10 m/s逐渐减速的,当t较小时,后机速度较大,追赶趋势明显,若保持该速度继续滑行,则必然形成冲突,因此当t<25 s,ΔGi,j(0)≤60,P[C(t)]恒为1.0。随着t逐渐增加,后机不断减速,t>50 s形成前快后慢状态,前机逐渐远离后机且后机速度进一步减小,冲突风险为0。ΔGi,j(0)越大,P[C(t)]=0对应时间范围越长,当ΔGi,j(0)=250,t在63~100 s内P[C(t)]=0。说明63 s后,后机与前机满足安全间隔且不存在追赶,两机已无冲突风险。
对比图5~图7可知,当后机与前机速度差越大、航空器之间间隔越小,越容易形成追赶,冲突风险值越大。当前机转入其他滑行道时,需综合考虑滑行道构型、转弯速度等限制,对后机及时发布减速指令,防止产生冲突。控制后机速度和扩大间隔虽然能减少冲突风险,但会降低滑行效率,造成滑行道资源浪费。若仅为两航空器配备最小安全间隔,则存在极大冲突风险,需连续不间断监视后机速度,防止出现危险接近。
为证实本文模型的实验结果与实际运行过程相符,深入分析相关数据。如图5~图7所示,当ΔGi,j(0)属于区间[90,110],三种运动状态下冲突风险均小于0.6且风险概率标准差小于0.1,以上数值与文献[13]仿真验证结论一致,且实际监视数据统计结果为:航空器在平行滑行道平均速度为4.82 m/s,航空器平均纵向间隔为94.3 m。表明实验结果符合实际运行过程。当P[C(t)]为0.8时,后机减速至停止等待,最大减速度为0.25 m/s2,该值与文献[14]中统计数据基本一致。
由此可知:当航空器平均滑行速度达到5 m/s时,管制员为前后跟随的航空器配备90~110 m滑行间隔,滑行冲突风险较小且变化趋势稳定,能保障安全且减少管制指令。利用本文模型计算跟随滑行冲突,当冲突概率大于0.8时,对后机进行预警告警,能减少避让冲突导致的滑行急减速,提高乘客乘机的舒适度。分析可知,本文模型可量化动态冲突风险,计算结果可靠、有效且实际运行过程相符,利用本文模型计算结果能为场面滑行提供冲突预警,提高机场运行安全水平。
3.3 实际运行数据验证及分析
采集并处理中南某机场场面监视雷达监测到的航空器滑行监视数据。图8为航空器跟随滑行的两种场景。根据实际机型及滑行道结构设置参数:ΔSi,j=50 m,飞机机身均为45 m,场景一前后机为CES5336、CSN3300,ΔGi,j(0)=78 m,Si(0)=423 m,场景二前后机为AFL221、CSN362,ΔGi,j(0)=82 m,Si(0)=498 m。利用本文模型、传统基于间隔的冲突模型[7],分别计算冲突解脱前91 s的P[C(t)](冲突风险),并对比分析不同模型的计算结果。

浅灰色条状区域为滑行道;黄色、绿色点迹分别为前机、后机每秒钟滑行轨迹点;CES5336、CSN3300、CES5336、CSN3300分别为航空器呼号;R、S、E、H、W为平行滑行道及联络道名称,位于滑行道右侧图8 跟随滑行场景及冲突概率比较 Fig.8 Comparison of following taxi scene and conflict probability
如图8所示,两种情况下后机与前机在同一条滑行道跟随滑行。情况一中,前机CES5336初始滑行速度为6 m/s快于后机,因此P[C(t)]随t逐渐减少,当其接近交叉口,速度逐渐减少至3 m/s,而后机CSN3300加速至5 m/s,P[C(t)]在41 s突然增长至0.45,且随t逐渐增加至0.55。由于CES5336滑行55 m即转入联络道,因此81 s后两机成分散趋势,冲突风险不断下降至0.31。情况二中AFL221与CSN362均接近跑道外等待点,根据机场管制规则,航空器在跑道外等待点必须得到指令才能继续滑行进入跑道,因此两机滑行速度较慢,均小于2.5 m/s,基本呈匀速等距离运动状态。71 s时,AFL221转入联络道进行减速,但由于CSN362速度较小,因此两机呈轻微的追赶趋势,且前机滑行50 m即离开共享滑行道,因此冲突风险较小,均值为0.267,曲线波动较小,标准差为0.008 7。
将本文模型与传统基于间隔冲突模型[7]进行对比,两种模型计算结果有明显差异。两种情况下,传统模型冲突风险均随时间增加而增大,而本文模型却呈现不同结果。情况一中,本文模型计算风险值先减少后增加最后再急剧减少趋势;而情况二中,本文模型风险值随时间变化很小,基本呈固定值。这是由于传统模型仅考虑单位时间的水平间隔变化,因此在后机速度增加初期,由于间隔未明显缩小,传统模型的风险值仍呈缓慢增加趋势,而本文模型可根据速度变化实时更新冲突概率,能及时反映出冲突趋势的突变,由此在后机提速的关键时刻,本文模型风险突然增加1.2倍。当前机离开共享滑行道时,但由于两机位置接近,传统模型判断冲突仍呈增长趋势,但实际上两机已形成分散滑行,冲突解脱[16],因此本文模型风险大幅度下降为0.3。同理情况二中,两机速度较慢,保持稳定水平间隔,因此冲突风险较小,但由于后机经过前机等待道口,距离减少导致传统模型判断冲突持续升高为0.39,是本文模型的1.3倍。
由此可知,本文模型对航空器速度变化更敏感,能如实反映速度变化对冲突趋势的影响;本文模型基于航空器滑行态势定量计算冲突概率,能有效避免由于等待位置接近而造成的虚警误警;本文模型基于运动位置和方向判断滑行风险,能整体预测冲突产生、加剧及消散趋势。综上所述,本文模型计算结果优于传统模型,更适用于实际航空器过程中的冲突判断与安全管理。
4 结论
提高机场场面运行效率和安全水平,合理判别滑行冲突风险,是我国民航研究热点问题。深入分析了航空器同向滑行时的冲突过程,综合滑行实时滑行速度、位置、管制规则和机身长度,建立了航空器跟随滑行动态冲突风险模型。为了进一步分析滑行速度、初始间隔等重要参数对冲突趋势的影响,进行了多次计算机数值模拟仿真,并就各相关参数的作用及影响范围进行了分析对比。仿真结果与实际数据验证均能表明,本文模型计算结果可靠有效,与实际运行过程相符,该模型能实时量化速度、位置、滑行趋势对冲突的影响,计算结果优于传统模型,因此能对航空器滑行安全评估、冲突预警告警提供技术支持。

