基于离散元法的螺旋喂料器流量计算修正

林 苑 徐长斌 周祥明 程帅鹏

(江西师范高等专科学校，江西 鹰潭 335000)

螺旋喂料器结构简单，更换方便，在粮食输送领域被广泛的应用。流量是评价螺旋喂料器性能的重要指标，螺旋喂料器结构参数的选取离不开流量计算式。实际应用中，采用传统的流量计算式所得值与实际试验值相差较大，严重影响到螺旋喂料器结构的合理设计。在螺旋喂料器结构参数优化方面，国内外学者已做大量研究，梅潇等[1]为使垂直螺旋输送机的流量计算模型更符合实际情况，采用Matlab软件的拟合功能，并结合试验所测流速完成了流量计算模型的修正，流量计算值更加符合实际；赵方超等[2]为提高农业纤维螺旋喂料装置的性能，采用Design-expert 11设计优化试验，确定了各个因素对螺旋喂料器性能的最佳组合；梅潇等[3]针对螺旋喂料流量计算不精确的问题，基于散体力学理论，考虑螺旋面和颗粒群升角的径向变化，推导出螺旋喂料器的流量计算式，提高了流量计算的精确性。

螺旋喂料器内物料运动情况较为复杂，且不能直接进行观察与检测，离散元法是专门用来解决不连续介质问题的数值模拟方法，采用离散元法可以有效解决此问题。在利用离散元法对螺旋喂料器仿真分析方面，国内外学者做了大量研究，郭创等[4]基于离散单元法建立了螺旋输送机仿真模型，并通过离散元仿真软件进行模拟，同时采用正交试验法得出螺旋输送机的最佳参数组合；朱鸿翔等[5]针对螺旋喂料器因输送机理复杂而常常根据经验来进行设计的问题，采用离散元法对影响螺旋喂料器性能的相关参数进行了研究；李勇等[6]基于离散单元法，分析了不同转速及填充率下螺旋输送的情况，并分析填充系数、流量及合力矩在输送中的影响，为螺旋输送机的结构设计提供依据。

针对螺旋喂料器实际流量检测值与传统计算式的计算值相差较大的问题，拟采用响应面试验对螺旋喂料器的流量计算式进行修正。考虑到实际试验的复杂程度，采用离散元仿真测定流量值与计算式计算所得值的比值作为响应，以对流量差值影响显著的螺距、转速、管径为因素，设计响应面试验，得到3个因素与响应值之间的二阶回归方程，由此进一步得到螺旋喂料器的流量计算式，为螺旋喂料器的设计计算提供参考。

1 基础理论

1.1 运动分析

对螺旋喂料器内物料的运动情况进行分析，有利于螺旋喂料器的结构优化设计。设螺旋喂料器螺旋升角为α，P合为r处的物料颗粒A上的力，此力可分解为切向和法向力，如图1(a)所示。

图1(b)为A的运动分析，A的合成速度可分解为轴向、圆周速度。设转速为n，可知

图1 物料受力分析

V合cosρ=ABsinα。

(1)

又因

(2)

可知

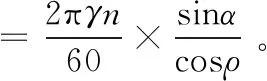
(3)

可知，圆周速度为

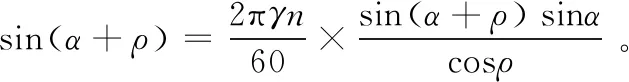
(4)

由式(4)，可知

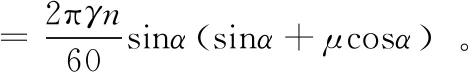
(5)

联立μ=tanα，得

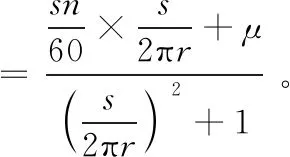
(6)

将式(6)对r求导，然后使对r的倒数为0，当在V圆值最大时，r值为

(7)

由速度分解，可知

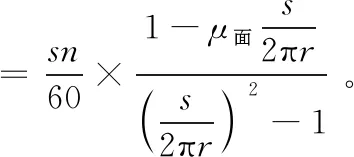
(8)

1.2 流量公式

由式(8)可知物料轴向速度的计算式，经验中，轴向速度常常简化处理为v=sn/60，投影面积A的计算也常常不考虑影响较小的内轴径d，由此得到螺旋喂料器的计算式为[7]：

Q=47D2φSnγCK，

(9)

式中：

Q——螺旋喂料器流量，t/h；

D——叶片外径，m；

φ——填充率；

S——螺距，m；

n——转速，r/min；

γ——物料容重，t/m3。

2 响应面试验

针对螺旋喂料器的流量计算公式计算结果与实际测定流量值误差较大的问题，因实际试验的复杂程度，以小米为研究对象，采用离散元仿真流量值与螺旋喂料器公式计算值的比值作为响应，以对流量比值影响显著的螺距S、管径D、转速n为变量设计响应面试验，对螺旋喂料器的流量计算式进行修正。

2.1 仿真参数

响应值的计算需要根据螺旋喂料器离散元仿真的结果，离散元仿真参数的确定，根据相关文献资料[8]，小米离散元仿真参数如表1所示。

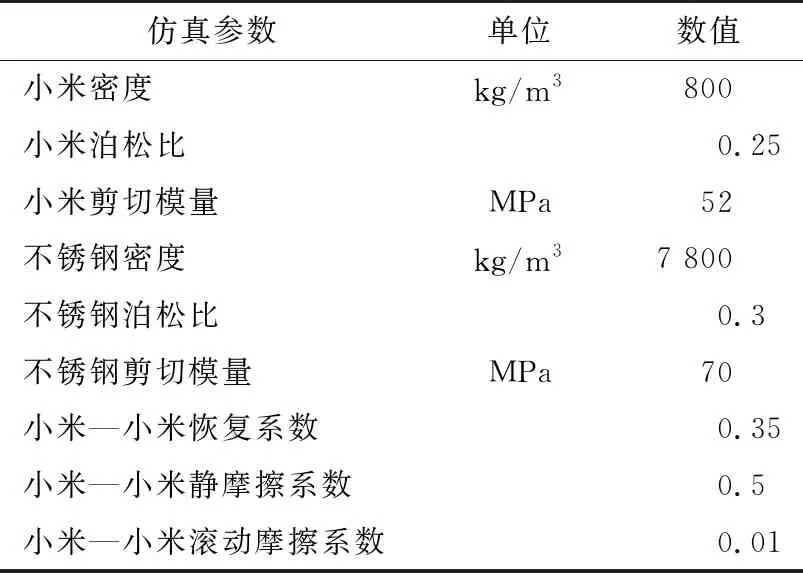
表1 离散元仿真参数表

2.2 试验因素

采用离散元仿真流量值与螺旋喂料器公式计算值的比值作为响应，以对流量比值影响显著的螺距S、管径D、转速n为变量设计响应面试验，结合设计要求及实际情况选取因素水平如表2所示。

表2 响应面试验水平表

2.3 试验设计

根据表2，试验设计选取3个中心点对误差进行评估，结果如表3所示。

表3 试验设计及结果

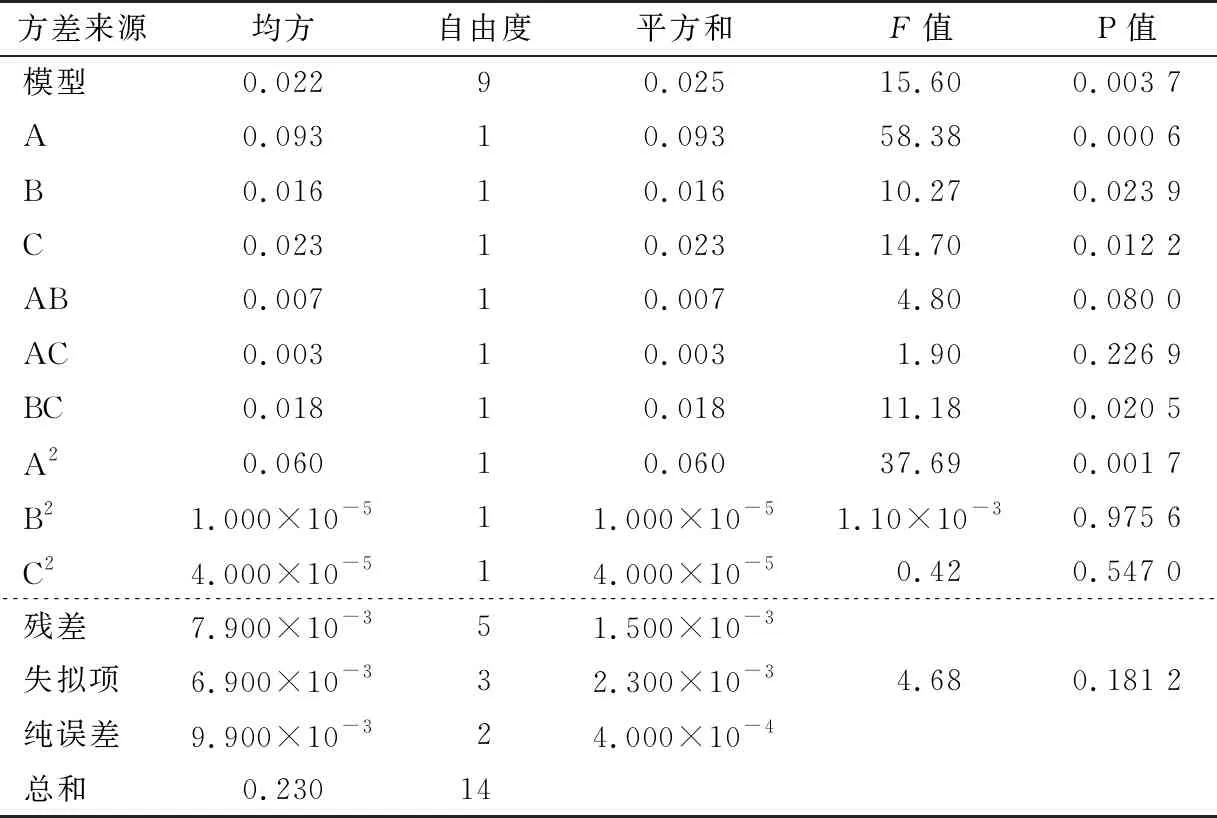
表4 试验模型方差分析†

根据表4结果，在保证模型良好前提下，剔除对响应值影响不显著的项(AC、B2、C2)，优化后的结果如表5所示，失拟项P=0.234 7；试验精密度Adep Precision=14.04。可知，模型较优化前有了很大的改善，优化后回归方程为：

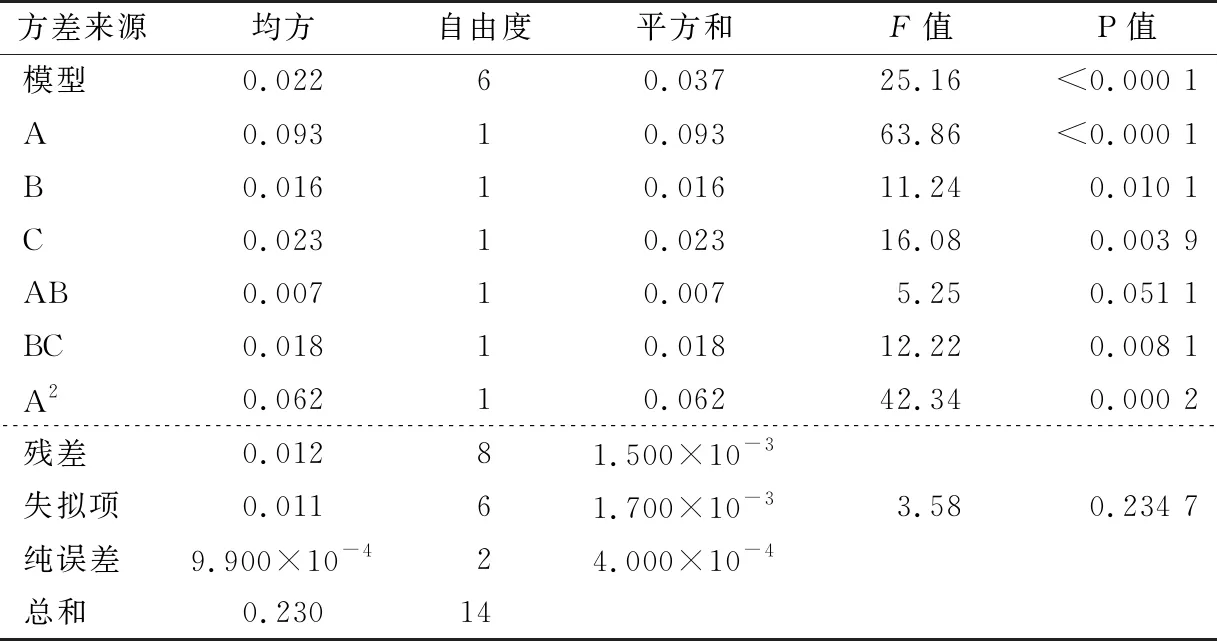
表5 试验优化模型方差分析†

Q=-5.11+0.209A-0.062B-0.028C+0.000 44AB+0.000 33BC-0.013A2。

(10)

修正后的螺旋喂料器的流量计算式可表示为：

Q=47D2Snγφ×(-5.11+0.209D-0.062S-0.028n+0.000 44DS+0.000 33Sn-0.013D2)。

(11)

2.4 响应面分析

根据优化回归模型方差分析结果可知，AB、BC的P值<0.05。在转速为80 r/min以及管径为颗粒间滚动摩擦系数90 mm 2种情况下，绘制AB及BC交互作用的响应曲面。由图2(a)可知，相对于管径，螺距的效应面曲线比较陡；由图2(b)知，相对于螺距，转速的效应面曲线比较陡。

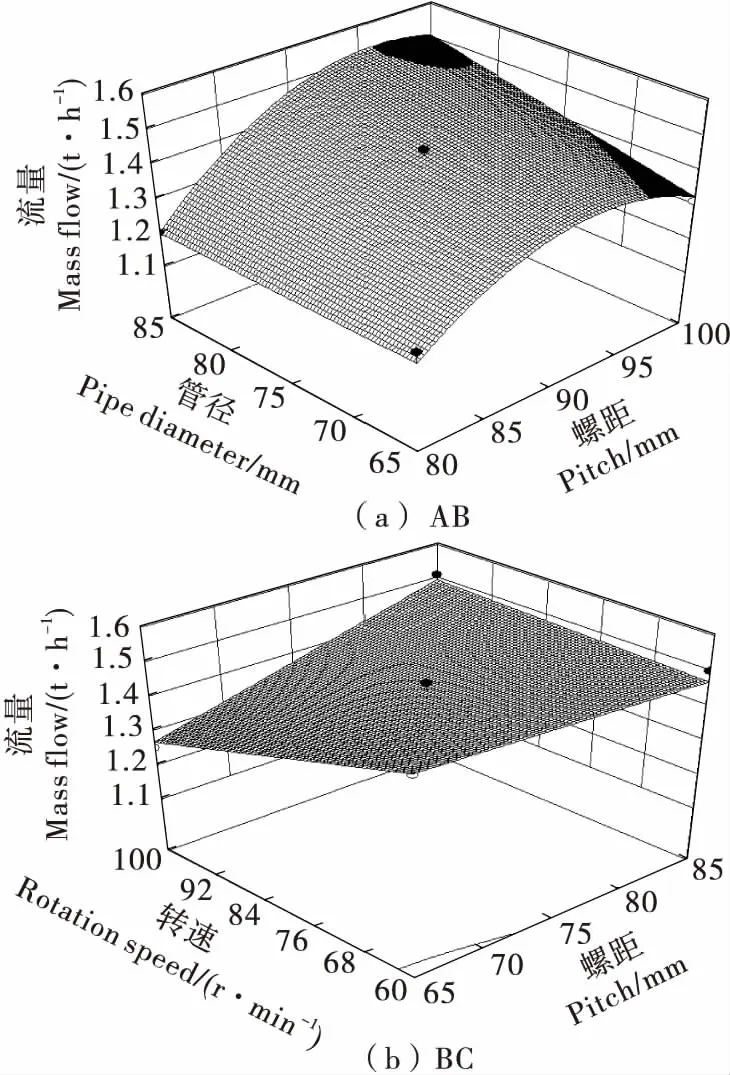
图2 AB与BC的交互效应图

3 仿真实验验证

3.1 设计要求

螺旋流量Q=1.0 t/h，物料为小米，物料综合特性系数A=65，填充率φ=0.53，物料容重r=0.51 t/m3，转速n=100 r/min，管径D=100 mm，螺距S=0.8D[9-11]。根据设计要求D、S、n的取值及式(11)可知，螺旋喂料器的流量计算值为1.210 t/h。

3.2 仿真模型

根据设计要求，建立螺旋喂料器的三维模型，然后转化为step格式后导入离散元软件进行仿真。结合相关文献[12-14]，颗粒仿真采用软球模型仿真模型如图3所示。

图3 仿真模型

3.3 仿真结果

待仿真结束后，采用两个稳定时间段对螺旋喂料器的流量进行检测，结果如图4所示。

由图4可知，螺旋喂料器的平均流量为1.258 t/h，与修正式计算流量值1.210 t/h误差为3.97%，表明了修正流量计算式的精确性。

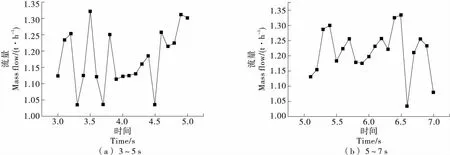
图4 螺旋喂料器流量检测图

4 结论

(1) 针对螺旋喂料器实际流量检测值与传统计算式的计算值相差较大的问题，采用响应面试验对螺旋喂料器的流量计算式进行修正。考虑到实际应用的复杂程度，采用离散元仿真测定流量值与计算式计算所得值的比值作为响应，以对流量差值影响显著的螺距、转速、管径为因素，设计响应面试验，得到3个因素与响应值之间的二阶回归方程，由此进一步得到螺旋喂料器的流量计算式。

(2) 为进一步验证流量计算式的可行性，根据设计要求用SolidWorks软件建立三维模型，并进行离散元仿真，发现仿真所得流量值为1.258 t/h，与修正式计算所得流量值1.210 t/h的误差为3.97%，表明了流量修正计算式的合理性，为螺旋喂料器的设计计算提供参考。

(3) 试验中以仿真流量与计算流量比值作为响应，因仿真存在一定的误差，修正所得的流量计算式可粗略求解，后续可根据试验设计，加工螺杆，对仿真流量修正公式的可行性进一步研究。