干扰因素对罗氏线圈测量精度的影响分析∗

卢山明 宋文武 黄 琛 乐天华

（1.中国舰船研究设计中心 武汉 430064）（2.武汉船舶设计研究院有限公司 武汉 430064）

1 引言

随着现代电力技术的不断发展，舰船电力系统所承载的容量越来愈大，传统的电流互感器在这样的场景下面临各种各样的问题［1］。传统电流互感器体积大、安装困难、抗电磁干扰能力差、电气绝缘性不佳，已不适合电力电子设备监测或测量的需求［2］。

目前舰船动力系统和电力系统结合构成综合电力系统是近年来新的发展思路和技术思想［3］，为了实现舰船电力系统的智能化和网络化，需要对相关电流电压信息进行监控。Rogowski线圈（以下简称罗氏线圈）由于其结构和测量原理方面的特点，受到了广泛的关注。与传统带铁心互感器相比，罗氏线圈传感器测量范围宽、精度高、无磁饱和现象、体积小、质量轻［4］，被广泛应用于瞬态大电流检测和脉冲功率技术领域［5］。

然而，在实际应用中发现，除了罗氏线圈自身结构会造成测量结果的相位误差［6］外，还存在外界电磁干扰［7］、被测导体安装位置等各种干扰因素都可能会对罗氏线圈的测量精度造成影响。常规分析方法有提出温度变化时骨架、线圈的变化差异及复合影响的分析方法［8］，也有对比多种规格线圈感应电流波形进行分析［9］，还有考虑绕线绕制方式的分析方法［10］。本文从罗氏线圈测量原理出发，采用数学推导的定量方法，研究有关外部干扰因素对罗氏线圈测量幅值精度的影响，并通过仿真模拟验证了相关推理。

2 基本原理

罗氏线圈基本结构较为简单，根据线圈骨架截面的不同，常见的有矩形横截面罗氏线圈和圆形横截面罗氏线圈。图1为矩形截面罗氏线圈原理图。其中，I为被测电流，Ra为骨架外半径，Rb为骨架内半径，h为骨架厚度，N为线圈匝数，u0是真空磁导率，r为距被测导线距离。假设导线为无限长，e0为线圈感应电压。根据安培环路定律有：

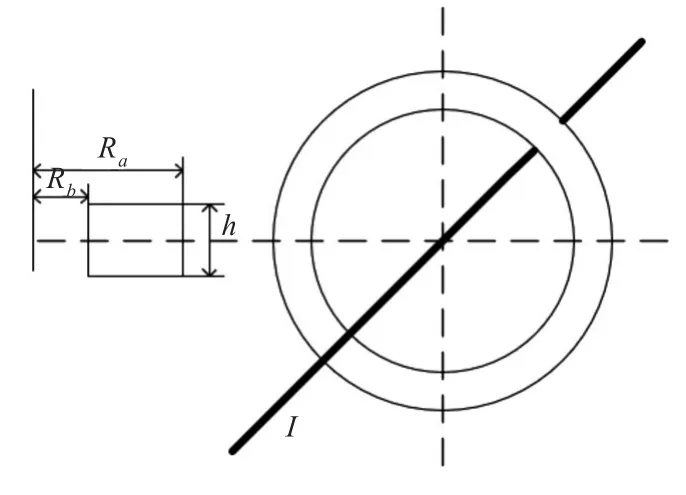
图1 矩形截面罗氏线圈原理图

当被测导线离线圈较远时，穿过线圈的磁通Φ0近似为

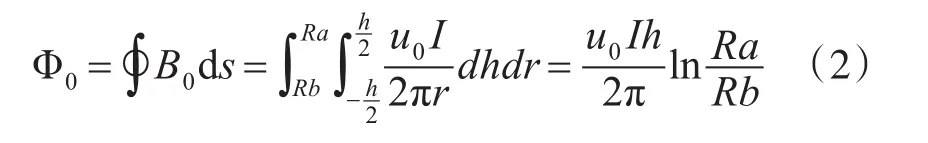
根据电磁感应定律有：

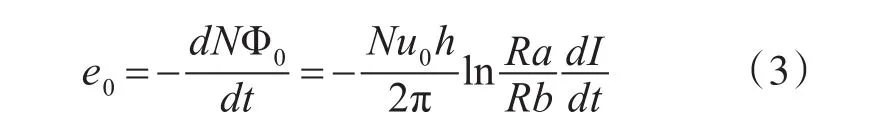
需要注意的是，安培定律使用过程中线性积分要求线圈宽度和厚度都为0。如果存在这种理想线圈，则罗氏线圈的输出将与路径的形状以及载流导体在线圈窗口内的位置无关。然而，实际线圈的螺旋绕组具有一定的厚度和宽度，从而上述结果分析产生的结果仅接近安培定律的严格要求［11］。

3 干扰分析

从上文可以看出，影响罗氏线圈测量精度的因素主要包括外部磁场干扰和导体位置。此外，当所有绕匝都具有完全相同的横截面并且围绕圆形路径完美均匀地分布时，罗氏线圈将产生最小误差［12］。因此，假设线圈为矩形截面罗氏线圈，且线圈绕制均匀。

3.1 导体偏移

当导体偏离线圈中心时，其周围产生的磁场分布相应的发生变化，线圈截面上某一点P对应的场强此时需要重新计算，简化后示意图如图2。

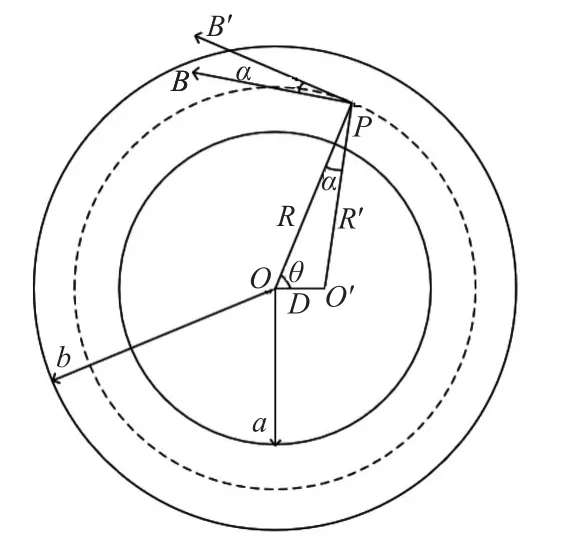
图2 待测导体偏移中心后的磁场示意图

其中，P为线圈截面上某一点，O为线圈中心，O'为导体偏移后的中心，D为导体偏移距离，B为偏移后在P点的磁场，B'为B垂直于线圈截面的分量，OP=R，O'P=R'。P处有，

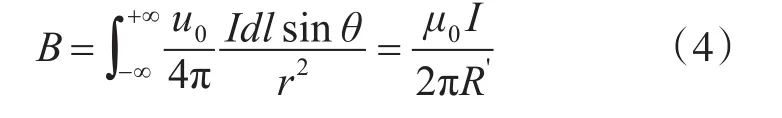
所以P点所在线圈截面上磁通量为

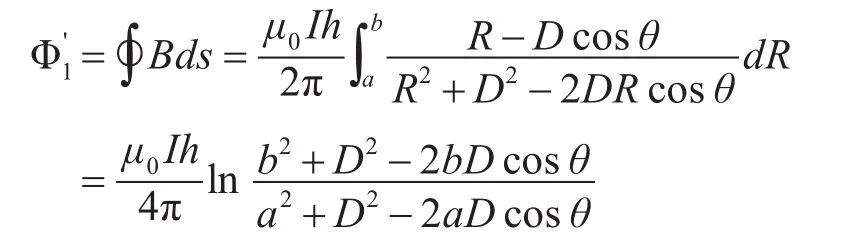
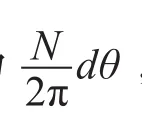
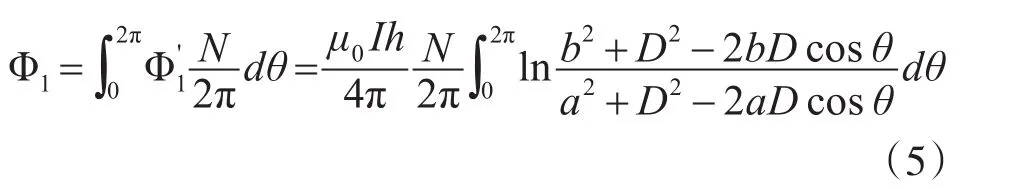
记k=b/a，t=D/a，m=D/b，上式可以改写为

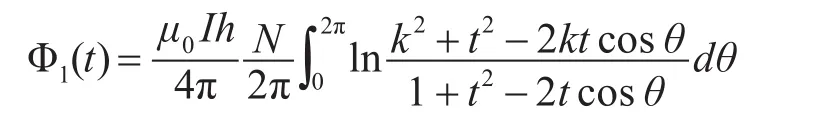
所以当导体发生偏移时相对误差为

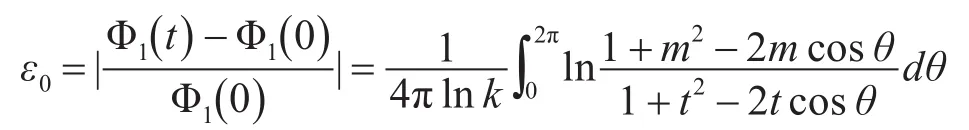
假设a=90mm，b=100mm，分别计算偏心度t为0～1时的相对误差如下。

可以看到，当偏心度小于0.8时，相对误差极小，而在0.8～0.9这段误差迅速上升。因此可以认为，只有当中心待测导体偏移到快要接触线圈时才会产生较大误差。所以，在安装过程中，要尽量保证中心导体偏移在较小范围内。

表1 相对误差ε0和偏心度t的关系

3.2 导体倾斜

本小节仅讨论中心待测导体发生倾斜但不发生偏移的情况，具体示意图如图3。

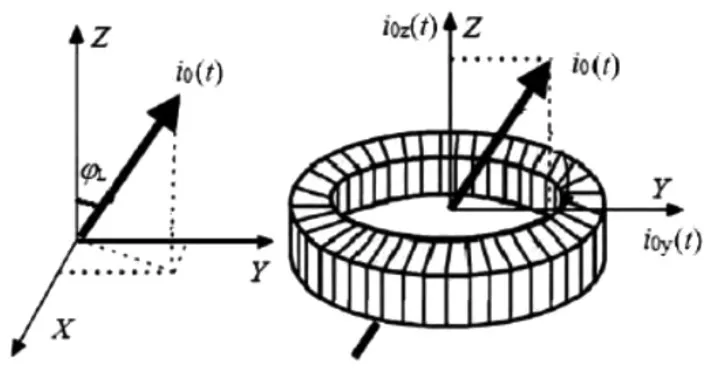
图3 待测导线发生倾斜时的示意图

所以导体上电流i0(t)在x，y，z三个方向上的分量可以表示为

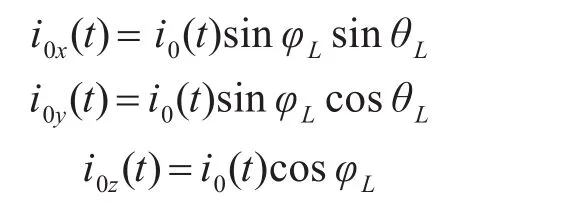
对于X，Y方向上的电流分量，它产生的磁场方向平行于线圈截面，因此不会对感应电压做贡献，主要由Z方向的电流分量产生线圈上的感应电压，对应的感应电压可以写为

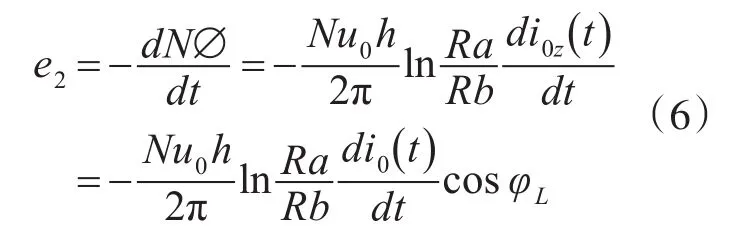
相应的相对误差可以表示为

由上式可以得出结论，当中心待测导体发生倾斜时，会对最终测量结果产生影响，且倾斜角度越大，误差越大。所以在实际测量安装时，要采取措施保证穿过线圈部分与线圈平面保持垂直。

4 仿真验证

首先，在3.1节导体偏移讨论中，默认了线圈匝数N是趋近于无穷大的，但是，实际的线圈匝数通常都是有限的，假设线圈是一个有限匝数N，其它参数和前文保持一致，在这种情况下，积分变化为累加求和，总的磁通可以表示为

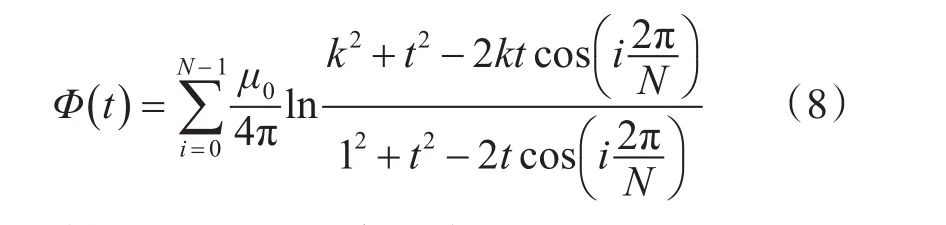
此时相对误差可以表示为

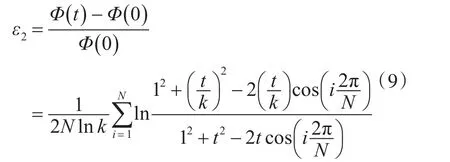
同样的假设，内径a=90mm，外径b=100mm，使用Matlab分别画出N=100，300，500时的相对误差ε2-t图像如下。

图4 相对误差ε2和偏心度t的图像

从图中可以看到随着匝数N的增大，同一偏心度对测量的影响越来越小。同时可以看出当偏心度小于0.9时，误差几乎可以忽略不计，但是随着偏移距离的继续增大，误差开始突然上升，整体趋势与N接近无穷时的情况类似。

为了更加准确地反映分析结果，使用Maxwell软件建立对应模型，其中内径a=90mm，外径b=100mm，匝数N=30，考虑感应电压大小为

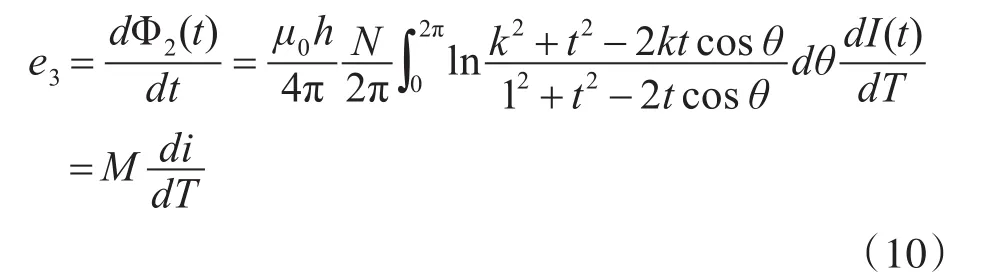
记互感系数M为

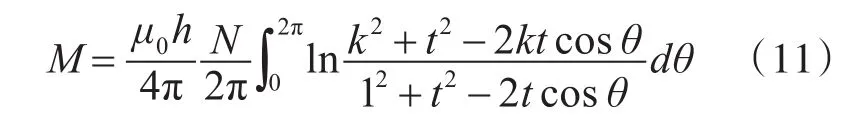
可以看到互感M的变化直接反应出感应电压的变化，所以在建立模型后，中心导线距线圈中心距离从0mm～80mm变化，每隔10mm进行一次仿真，得到互感M的变化曲线如下所示。

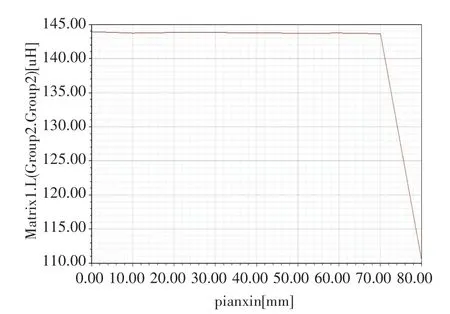
图5 偏心距离和互感系数M的Maxwell仿真结果

可以看到当偏心距离在0～70mm时，互感系数M几乎没有变化，70mm～80mm时互感系数迅速减小。也就是说，在上述线圈模型中，当被测导体偏离中心0～70mm时，感应电压测量结果几乎不变，偏离中心70mm～80mm时，相对误差迅速增大。该模型验证了之前的定量分析。

5 结语

本文分别从被测导体偏离线圈中心，被测导体倾斜两方面分析了对罗氏线圈最终精度的影响。分析表明，上述因素若不加控制都会对最终精度产生影响。为了避免导体偏心或倾斜的影响，在安装和使用过程中，需要对被测导体进行固定。然而，除了文中分析的因素，罗氏线圈自身绕制方式，工作环境等同样会对测量精度产生影响，需要后续研究。