基于分段粒子群算法的梯级水库多目标优化调度模型研究

吴志远，黄显峰，李昌平，刘志佳，颜山凯

(1.河海大学 水利水电学院，江苏 南京 210098; 2.中国华电集团有限公司福建分公司,福建 福州 350013; 3.华电福新能源股份有限公司 池潭水力发电厂，福建 泰宁 354400)

1 研究背景

随着我国水电能源的持续开发，如何合理地优化水库群的联合调度越来越受到行业内的重视。一方面，随着流域电站数目的增加、计算时间步长的减小，上下游水力和电力联系进一步增强，约束条件更加难以处理，问题复杂度呈指数型增长[1]；另一方面，梯级水电站需要综合考虑各方面效益，目标数的增多进一步增加了问题的复杂度[2-3]。可见水库群优化调度是一个复杂的高维、非线性、强耦合的多目标优化问题[4]。

近年来，国内外学者将智能算法应用于水库优化调度领域，取得了不错的效果。冯仲恺等[5]从种群初始化、进化和变异等方面提出了改进量子粒子群算法，应用于乌江梯级调度；Baltar等[6]建立了基于多目标粒子群算法的水库群优化调度模型，分析了其解集的收敛性和多样性；薛保菊等[7]提出了单纯形混合遗传算法(SM-HGA),并将其应用于水电站水库优化调度中，证明了其具有收敛速度快、收敛率高的优点；周建中等[8]将粒子群算法(PSO)嵌入到蛙跳算法(SFLA)的分组框架中，提出了多目标混合粒子群算法(MOSPSO)，克服了PSO收敛速度慢、易陷入局部极值[9-11]的问题。

虽然国内外学者进行了大量的研究工作并取得了一定进展，但现有的方法仍然存在一些瑕疵。比如，大部分现有的智能优化算法更适用于以月(或旬)为时间步长、计算时段数目较少的水库优化调度问题，一旦应用于时间步长较小、计算时段数目较多的精细度较高的水库优化调度模型仍会出现计算效率低、甚至难以得到可行解的情况。例如，刘攀等[12]尝试将遗传算法和动态规划-遗传算法应用于以旬为计算时段的清江梯级电站多年连续优化，遇到了决策变量多、生成可行解难度大的问题，计算结果并不十分理想。这是由于相同调度周期下，时间步长的减少增加了问题的维度，减弱了计算时段内出力、下泄流量等指标的均化效应[13]，导致各种约束更难以得到满足，最终导致算法寻优效率的降低。由此可见，研究适用于求解时间步长较小、计算时段数目较多的水库优化调度问题的算法具有一定的价值。

本文提出了分段粒子群算法(piecewise particle swarm optimization，PPSO)、多目标分段粒子群算法(multi-objective piecewise particle swarm optimization，MOPPSO)来对时间步长较小、计算时段数目较多的水库多目标优化调度问题进行寻优，并通过闽江流域金溪梯级水库优化调度的实例应用，验证了其求解梯级水库多目标优化调度问题的优越性和工程实用性。

2 梯级水库多目标优化调度模型

2.1 目标函数集

2.1.1 发电效益最大目标 考虑到市场环境下梯级水电站中各电站电价不同，本文通过各电站电价相对于龙头电站电价的比例，折算一个调度周期内的梯级水库总发电量，公式如下：

(1)

式中：F1为发电效益目标，kW·h；M为电站数目;i为电站序号，i=1，2，…，M;T为计算时段个数;t为计算时段序号，t=1，2，…，T;ki为第i水电站电价相对龙头电站电价的比值；Ni,t为第i水电站在t时段的出力，kW;Δt为计算步长，h。

2.1.2 防洪减灾目标

(1)最高水位最小目标。对于库区上游，调度期内最高水位越小，上游的搬迁或淹没损失就越小。目标公式如下：

F2=min(maxZt)

(2)

式中:F2为上游的防洪目标，m；Zt为梯级水库中龙头水库t时段的坝前水位值，m。

(2)最大下泄流量最小目标。对于下游河流，洪水期下泄流量越小，下游受淹没的可能性和损失就越小。目标公式如下：

F3=min(maxQxi,t)

(3)

式中:F3为下游防护区的防洪目标，m3/s;Qxi,t为第i个水库t时段的下泄流量，m3/s。

2.2 约束条件

(1)水量平衡约束

Vi,t=Vi,t-1+(Qri,t-Qxi,t)Δt-Ei,t·Si,t-Di,t

(4)

式中：Vi,t-1、Vi,t分别为t时段初、末期的水库蓄水量，m3；Qri,t、Qxi,t分别为第i个水库t时段的入库流量和下泄流量，m3/s；Ei,t为第i个水库t时段的蒸发深度，m；Si,t为第i个水库t时段的水库面积，m2；Di,t为第i个水库t时段的渗漏损失水量，m3。

(2)水位约束

Zi,t,min≤Zi,t≤Zi,t,max

(5)

式中：Zi,t,max、Zi,t,min分别为第i个水库t时段的水位上、下限，m。

(3)发电流量约束

Qi,t,min≤Qi,t≤Qi,t,max

(6)

式中：Qi,t,max、Qi,t,min分别为第i个水库t时段的水电站发电流量上、下限，m3/s。

(4)电站出力约束

Ni,t,min≤Ni,t≤Ni,t,max

(7)

式中：Ni,t,max、Ni,t,min分别为第i个水库t时段的水电站出力的上、下限，kW。

(5)下泄流量约束

Qxi,t,min≤Qxi,t≤Qxi,t,max

(8)

式中：Qxi,t,max、Qxi,t,min分别为第i个水库t时段的下泄流量上、下限，m3/s。

上述所有变量均为非负。除此之外，针对不同流域的特点，还可能包括生态、航运等约束。

3传统智能优化算法在水库调度问题中寻优困难的原因分析

3.1 寻找可行解效率低下的原因分析

以寻找某水库优化调度问题可行解为例，将其各时间节点的水库水量作为决策变量进行实数编码。当下泄流量、出力等指标有强约束时，在解向量中，某些时间段的水库水量对变化较敏感，一旦其中某时间节点的水量发生改变，就容易导致约束的破坏。图1为迭代过程中某一解向量所表示的水库水量变化过程线，如图1中实线所示，此解向量的第4、7时段不满足约束，第2、3、5、6时段满足约束条件但某些指标值接近约束边界，此时，称第4、7时段为约束不满足段，第2、3、5、6时段为恰满足段。可见，单独调整第5时间节点的水量a会导致第4、5时段的水库下泄流量的改变，从而导致第4时段约束的破坏程度变大或者第5时段约束被破坏；同理，调整a1容易导致第5、6时段的约束被破坏；调整水量a2会使第7时段约束的破坏程度变大或者第6时段约束被破坏。此时，称第5、6时段为水量结构敏感段；同理，第3时段亦为水量结构敏感段。进化中，解向量内交替出现的约束不满足段和水量结构敏感段中的变量单独变化时，约束破坏程度往往变大，严重降低了算法寻找可行解的效率。

值得注意的是，第1时段满足约束且各指标值离约束边界较远，称其为过满足段。可以看出，适当改变水量b2不会使约束破坏程度增大，故b2在恰满足段内部，但不属于水量结构敏感段。

传统智能优化算法降低第4时段的约束破坏程度非常困难。成功率较大的方法是恰好b2、b1、b依次发生变异，在维持第2、3时段满足约束的前提下，增加第4时间节点水量至b′，于是第4时段的约束破坏程度得到降低(图1)。

需要说明的是图1所示只是相对简单的情况。在时间步长小、计算时段数目多的水库优化问题中，生成可行解的难度很高，传统智能算法极易遇到解向量内约束不满足段与水量结构敏感段交替出现、且水量结构敏感段往往包含几个、十几个时间节点的情况，严重影响其计算效率。进化中，约束不满足段的始末水量变化程度很小，导致其段内各变量达到最小的约束破坏程度后基本就不再变化了。

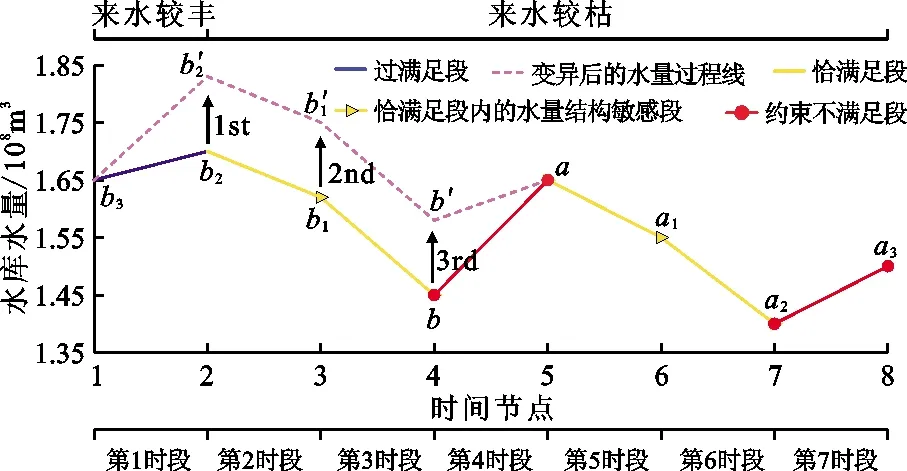
图1 迭代过程中某一解向量所表示的水库水量变化过程线

3.2 进入可行域后寻优效率低下的原因分析

进入可行域后，传统智能优化算法容易遇到水量结构敏感段过长、段数过多的问题。可见：(1)进化中，直接在水量结构敏感段内进行进化操作容易破坏约束，将导致产生大量不可行解，从而影响算法的效率；(2)迭代一定次数之后，如果水量结构敏感段所在的恰满足段的始、末水量不变，那么其段内的水量变化程度将会很小，这种情况会对计算效率产生影响。

可以看出，进化算法在解时间步长较小、计算时段数目较多的水库调度问题时，为提高其运算效率，要解决两大问题，即进化中，在过长的水量结构敏感段内进行进化操作，导致产生大量不可行解的问题和约束不满足段、恰满足段的始、末水量变化程度低的问题。

4 分段粒子群算法和多目标分段粒子群算法

针对上述原因，本文将水库多目标调度问题的寻优过程分为搜索可行解、可行域内搜索Pareto前沿两大阶段，并提出分段粒子群算法(PPSO)以及多目标分段粒子群算法(MOPPSO)来对此问题进行求解。所提出的算法以粒子群算法(PSO)为基本框架(PSO的计算步骤见文献[14])，通过引入约束破坏向量、分段操作和特殊变异操作的改进策略来优化进化过程，强化迭代中的种群质量；此外，在可行域内搜索Pareto前沿阶段，MOPPSO采用了“分解聚合”求Pareto解集的改进策略，使得所得解集尽可能接近多目标问题的真实Pareto前沿。具体改进策略描述如下。

4.1 约束破坏向量

在处理水库调度问题约束时，罚函数法虽是被使用频率较高的方法，但其缺点明显：(1)罚因子的选择十分困难，其过大、过小都会对计算结果产生影响[15]；(2)惩罚项无法携带解向量的约束被破坏的时段的信息。于是，本文提出约束破坏向量的概念，将其引入双适应度法的框架来对复杂约束条件进行处理，同时也为下文的分段操作提供依据。

约束破坏向量是元素为0～1的一种向量，其各元素对应着某个解在各时段的约束被破坏的程度，其模代表总时段的约束破坏程度之和，称为约束破坏度。以出力约束和下泄流量约束为例，约束破坏向量与约束破坏度公式如下：

(9)

(10)

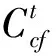
本文在处理复杂约束条件时，利用双适应度法的思想，把目标值作为主适应度、约束破坏度作为副适应度。进化时，个体首先向此代副适应度最优个体的方向进化，有多个个体副适应度相同时，再向其中主适应度最优的个体的方向进化。其优点是：(1)避免了罚因子的选取；(2)进入可行域后，规避了最优解为不可行解的情况；(3)约束破坏向量记录了个体各时段约束破坏程度的信息，为分段操作提供依据。

4.2 分段操作和特殊变异操作

在迭代时，PPSO、MOPPSO首先利用约束破坏向量，对解向量进行分段操作：通过现有约束得到约束破坏段；适当调整现有约束测出恰满足段、过满足段；根据各段连接关系得到水量结构敏感段。进化时，算法除了进行粒子群中各个个体的速度和位置的更新外，还进行特殊变异操作：

(1)当变异点落入过满足段时，一定概率下变异点根据其所在时间节点把解向量分成前、后两个大段，前段或后段的所有的水量都增加或减少相同变异值，其他概率下此变异点单独变异。例如，第n个时间节点处于某一过满足段内部，此节点的变量发生变异时，公式如下：

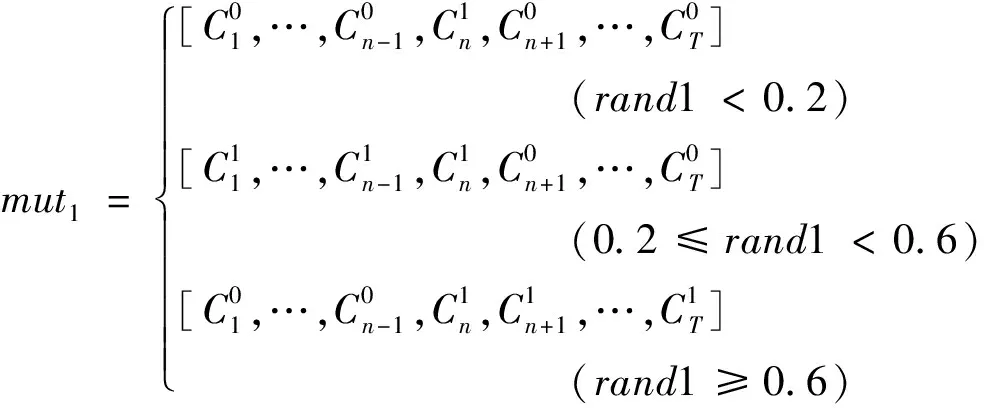
(11)

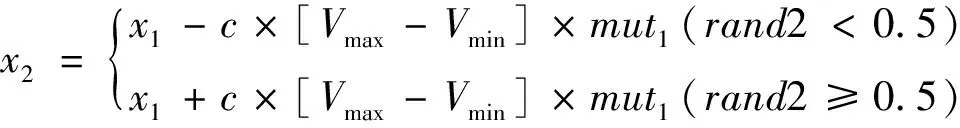
(12)

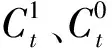
(2)当变异点落入恰满足段时，首先判断变异点位于水量结构敏感段内还是其他时间节点，如果落入水量结构敏感段，那么整个恰满足段的水量都增加或减少相同变异值，如果落在其他时间节点，则单独变异。例如，第n个时间节点处于恰满足段[l,m]内部，此节点的变量发生变异时，公式如下：

(13)

(14)

式中：mut2为恰满足段内变异的特殊变异向量；rand为[0,1]内随机数；其余变量含义同上。

(3)当变异点落入约束不满足段时，首先判断此段与过满足段、恰满足段的连接关系，如果此段前后均为过满足段，除去最前的时间节点的约束不满足段的水量都增加或减少相同变异值，如果一端为恰满足段、另一端为过满足段时，除去与恰满足段连接的时间节点的约束不满足段的水量都增加或减少相同变异值，如果前后均为恰满足段，一定概率下此变异点单独变异，其他概率下不变异。例如，第n个时间节点处于约束不满足段[l,m]内部，此节点的变量发生变异时，公式如下：

(15)

(16)

式中：mut3为约束不满足段内变异的特殊变异向量；其余变量含义同上。

特殊变异方式示意图见图2(流程可见图4)。

图2 分段粒子群算法部分变异方式示意图

特殊变异操作的优点为：(1)避免了水量结构敏感段、约束不满足段内的变量单独变异导致约束破坏度的增加，避免了迭代中出现大量不可行解的情况，提高了计算效率；(2)约束不满足段的水量的整体增加，有助于降低此段出力约束的破坏度，水量结构敏感段的整体抬升可以使得敏感段中的一部分时段不再敏感，有助于过长的水量结构敏感段的解体；(3)此算法的各段之间的水量变化方式直接增加了各段的始、末水量变化的概率，有助于提高计算效率。

特殊变异操作效果示意图如图3所示，由图3可以看出，变异点落入原水量结构敏感段，使其整体抬高，最终降低了虚线段的约束不满足段的约束破坏度。

图3 特殊变异操作效果示意图

4.3 求Pareto解集的“分解聚合”策略

进入可行域后，MOPPSO将多目标问题的求解过程分为两大步骤：(1)分解寻优步骤。将多目标问题分为多个单目标问题，分别进行寻优，使得到的各问题最优个体尽可能接近多目标问题的真实Pareto前沿。(2)聚合寻优步骤。开始寻找Pareto解集：首先生成初始种群，然后将分解寻优步骤得到的多个单目标问题的最优个体替换初始种群中的多个个体进行寻优，最终得到Pareto解集。

上述“分解聚合”求解策略的优点在于：(1)可以使最终得到Pareto解集尽可能接近多目标问题的真实Pareto前沿；(2)先使解集中的某些解优先接近真实Pareto前沿，再在真实Pareto前沿附近搜索Pareto解集的其他解，完善解集的多样性，避免了算法在进化中为还未接近真实Pareto前沿的解集的多样性花费过多的时间。

4.4 种群排序与个体进化

对于PPSO、MOPPSO算法，种群排序与个体进化密不可分。

种群排序方面，对于单目标问题，PPSO利用双适应度的思想，首先通过约束破坏度对个体进行升序排序，多个个体的约束破坏度相同时，再利用目标函数值对这些个体进行从优到劣的排序。对于多目标问题，在分解寻优步骤，MOPPSO的种群排序方式与PPSO相同；在聚合寻优步骤，MOPPSO首先通过约束破坏度对个体进行升序排序，多个个体的约束破坏度相同时，再对这些个体进行非劣排序和拥挤距离排序[16]。

个体进化方面，对于单目标问题，PPSO首先进行位置和速度的更新，再根据概率判断是否进行特殊变异操作。PPSO的特殊变异公式同上述，位置和速度的更新公式如下：

(17)

(18)

对于多目标问题，MOPPSO处于分解寻优步骤时，个体进化的公式与PPSO一致；处于聚合寻优步骤时，分解寻优步骤得到的个体与此代的Pareto解中排序较高的个体不进行进化，其他个体的特殊变异公式和位置的更新公式同上述，速度的更新公式如下：

(19)

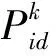
4.5 PPSO计算步骤

PPSO的运算流程见图4。以任意目标函数为主适应度函数，PPSO搜索水库调度问题可行解的计算步骤可总结如下：

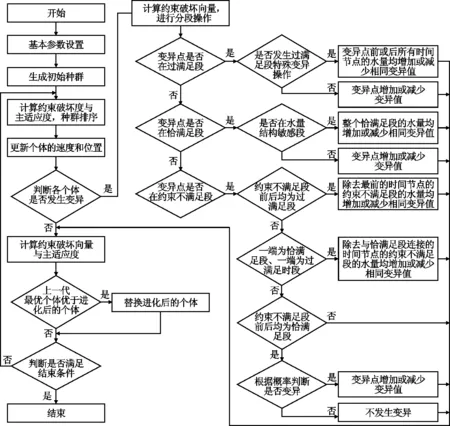
图4 PPSO的运算流程图

Step 1 算法基本参数设置；

Step 2 采用各水库各时间节点的水量作为决策变量进行编码，产生初始种群；

Step 3 计算各个个体的约束破坏度与主适应度；利用双适应度法对种群进行排序；

Step 4 更新个体的速度和位置；

Step 5 根据概率判断是否发生变异，如需变异则计算约束破坏向量、进行分段操作、特殊变异操作；

Step 6 计算个体的约束破坏向量与主适应度；上一代最优个体与其进化后的个体进行比较，如果优于进化后的个体则将其替换；

Step 7 判断结束条件，如果有个体的约束破坏度达到0(即已进入可行域)则进入Step 8，如果不满足结束条件转入Step 3；

Step 8 结束。得出优化调度可行解。

4.6 MOPPSO计算步骤

MOPPSO的运算流程见图5。求Pareto解集计算步骤归纳如下：

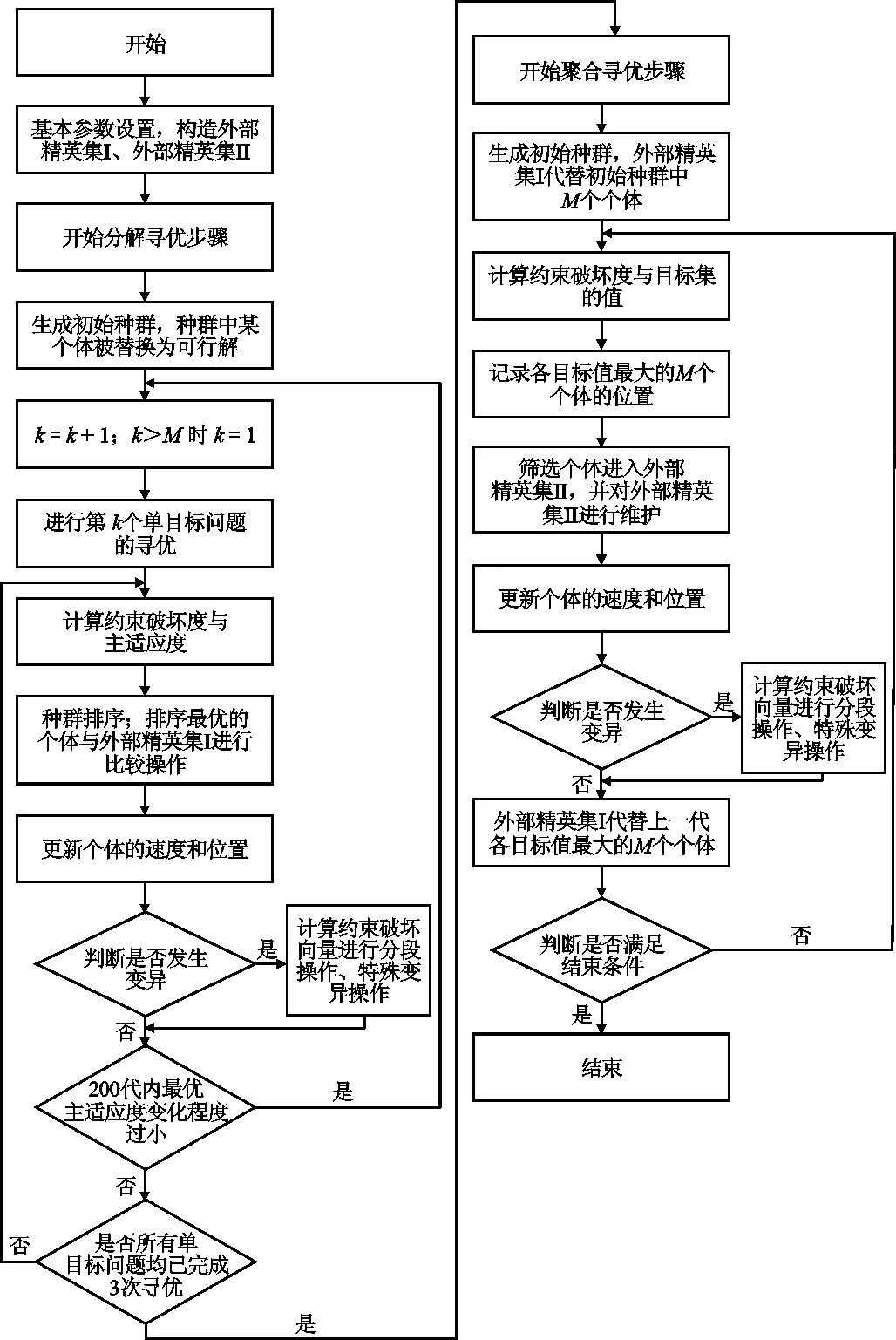
图5 MOPPSO的运算流程图

Step 1 算法基本参数设置，构造外部精英集Ⅰ、外部精英集Ⅱ；

Step 2 开始分解寻优步骤；采用各水库各时段水量作为决策变量进行编码，生成初始种群，其中某一个体被替换为PPSO解得的可行解；

Step 3 将多目标问题分为M个单目标问题，循环进行M个单目标问题的寻优：k=1时，进行第1个单目标问题的寻优，k=2时，进行第2个单目标问题的寻优，……，k=M时，进行第M个单目标问题的寻优，k=(M+1)时，进行第1个单目标问题的寻优……;

Step 4 计算约束破坏度与目标值；以双适应度法对整个种群进行排序，排序最优的个体如果优于外部精英集Ⅰ的对应单目标问题的个体，则替换其对应的个体，否则被外部精英集Ⅰ中对应的个体所替换；

Step 5 更新个体的速度和位置；

Step 6 根据概率判断是否发生变异，如需变异则计算约束破坏向量、进行分段操作、进行特殊变异操作；

Step 7 判断结束条件：如果200代内目标函数的最优值变化程度过小，则k=k+1,进入Step 3；如果所有单目标问题都已完成3次寻优，则进入Step 8；其他情况进入Step 4；

Step 8 开始聚合寻优步骤；生成初始种群；外部精英集Ⅰ中的个体代替种群中的M个个体；

Step 9 计算约束破坏度与目标集的值，对种群进行排序;将此代的Pareto解集加入外部精英集Ⅱ；剔除外部精英集Ⅱ的支配解，用小生境法[17]对外部精英集Ⅱ进行维护，剔除部分位置过密集的解；

Step 10 分解寻优步骤得到的个体与此代的Pareto解中排序较高的个体不进行进化，其他个体更新速度和位置；

Step 11 据概率判断是否发生变异，如需变异则计算约束破坏向量、进行分段操作、特殊变异操作；

Step 12 判断是否满足结束条件：如果达到最大迭代次数则进入Step 13，否则进入Step 9；

Step 13 结束。外部精英集Ⅱ为多目标问题的Pareto解集。

5 实例分析

5.1 研究区域概况

金溪是闽江上游的二级支流，位于福建省境内，流域面积7 201 km2。金溪流域的池潭水电站于1980年建成发电，其坝址控制流域面积4 766 km2，总库容8.7×108m3，是金溪干流梯级开发的龙头水库。池潭水电站以下河段有8个水电站，即良浅、大言、黄潭、孔头、范厝、高唐、谟武和贵岭水电站。金溪流域中仅池潭水库具有不完全年调节能力，其他水库无调节能力，整体调节性能差。各电站基本参数见表1。

表1 金溪干流各梯级水电站基本参数表

5.2 计算结果对比

5.2.1 各算法求解可行解的结果对比 以平水年(50%)的径流数据为基础，以日为时间步长将调度期划分为365段，分别利用分段粒子群算法(PPSO)、粒子群算法(PSO)、遗传算法(GA)、带变异的改进粒子群算法(IPSO)、蛙跳框架的混合粒子群算法(SPSO)[8]寻找上文所述的梯级水库多目标优化调度模型的可行解；进入可行域后，再分别利用多目标分段粒子群算法(MOPPSO)、NSGA-Ⅱ算法、多目标粒子群算法(MOPSO)、蛙跳框架的多目标混合粒子群算法(MOSPSO)进行Pareto解搜索计算。从可行解搜索、Pareto解搜索两个方面进行各算法的对比。对比结果如表2所示，各算法的约束破坏度随迭代次数下降曲线见图6。

表2 各算法求解可行解结果对比

图6 各算法的约束破坏度随迭代次数下降曲线

5.2.2 各算法的Pareto解集质量评价(quality indicator, QI) 目前，QI主要评价解集3个方面的性能：(1)解集与真实Pareto前沿的逼近程度(收敛性)；(2)解集在目标空间分布的均匀程度(分布均匀性)；(3)解集在目标空间分布的广泛程度(分布广泛性)[18]。

本文采用如下指标来评价各算法得到的解集的质量：

(1)超体积指标(hypervolume)。超体积指标度量的是Pareto解集与参照点围成的目标空间中的维区域的体积[19]。公式如下：

(20)

式中：HV为超体积指标值；δ为Lebesgue测度，用来测量体积;aref为参考点;Y为目标空间；A为非支配解集。

超体积指标度量解集所支配的区域的尺寸大小，HV值越大，表示其越逼近真实Pareto前沿，分布均匀性和分布广泛性越好，对应算法的收敛性和多样性越好。

(2)多次计算所得解集的目标函数最优值的平均值。取3次计算得到的解集中各目标函数最优值的平均值,可描述算法的优化水平。计算结果见表3、4。

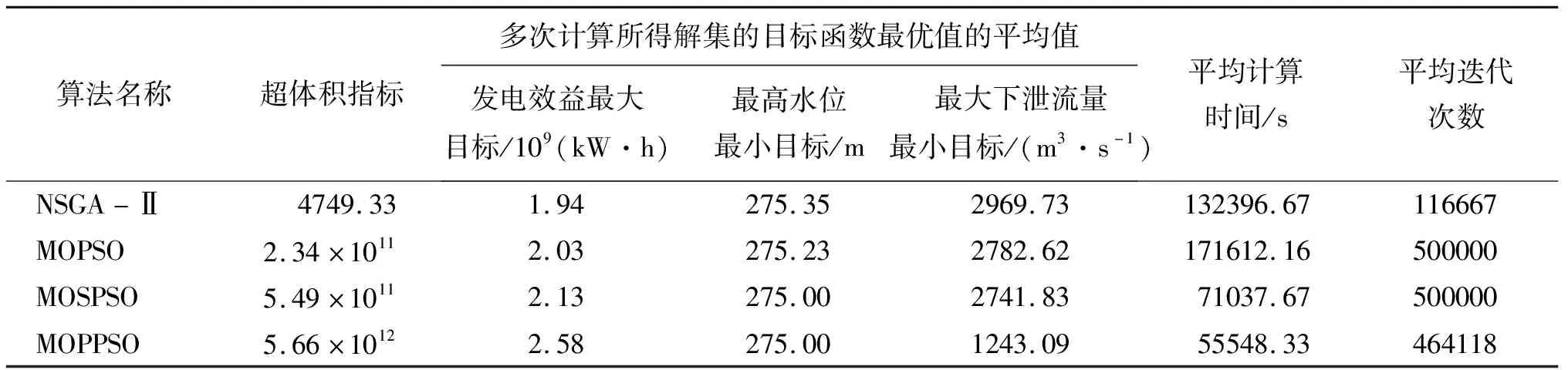
表3 各多目标算法计算结果汇总表

5.3 计算结果分析

从以上计算结果对比中可以看出，PPSO、MOPPSO在时间步长较小、计算时段数目较多的水库优化问题中较其他算法具有明显优势：

(1)从可行解搜索方面来看，PPSO算法较其他算法具有极大优势。除PPSO算法外，其余算法在可行解搜索上寻优效率低下，均未在20 000代内搜索出可行解，且搜索时间普遍在1 100 s以上。其中，表现较好的IPSO算法的结果虽然较其他算法的结果更接近可行域，但用时也达到了1 915.91 s。从图6可以看出，除PPSO算法外，其余各算法的约束破坏度下降速度均在1 500代前就开始放缓，并且呈现约束破坏度越小，下降速度越慢的趋势。这主要是由于传统智能优化算法无法解决本文第3节所描述的“在水量结构敏感段内进行进化操作导致产生不可行解、各段的始末水量变化程度低”的两大问题。值得注意的是，从PSO、GA以及IPSO的约束破坏度下降曲线可以看出，带有传统变异操作的智能优化算法虽然运算效率十分低下，但对比没有变异操作的算法仍具一定优势。这是由于传统的变异操作拥有概率上的“全局搜索”能力，但在具有强约束、时间步长较小、计算时段数目较多的水库优化问题中，这种能力被极大地削弱了。

PPSO算法在可行解搜索方面表现出色，进入可行域的迭代次数7 561次，用时488.29 s，运算效率优于其他算法。可见PPSO算法在可行解搜索方面是具备极大的优势的。

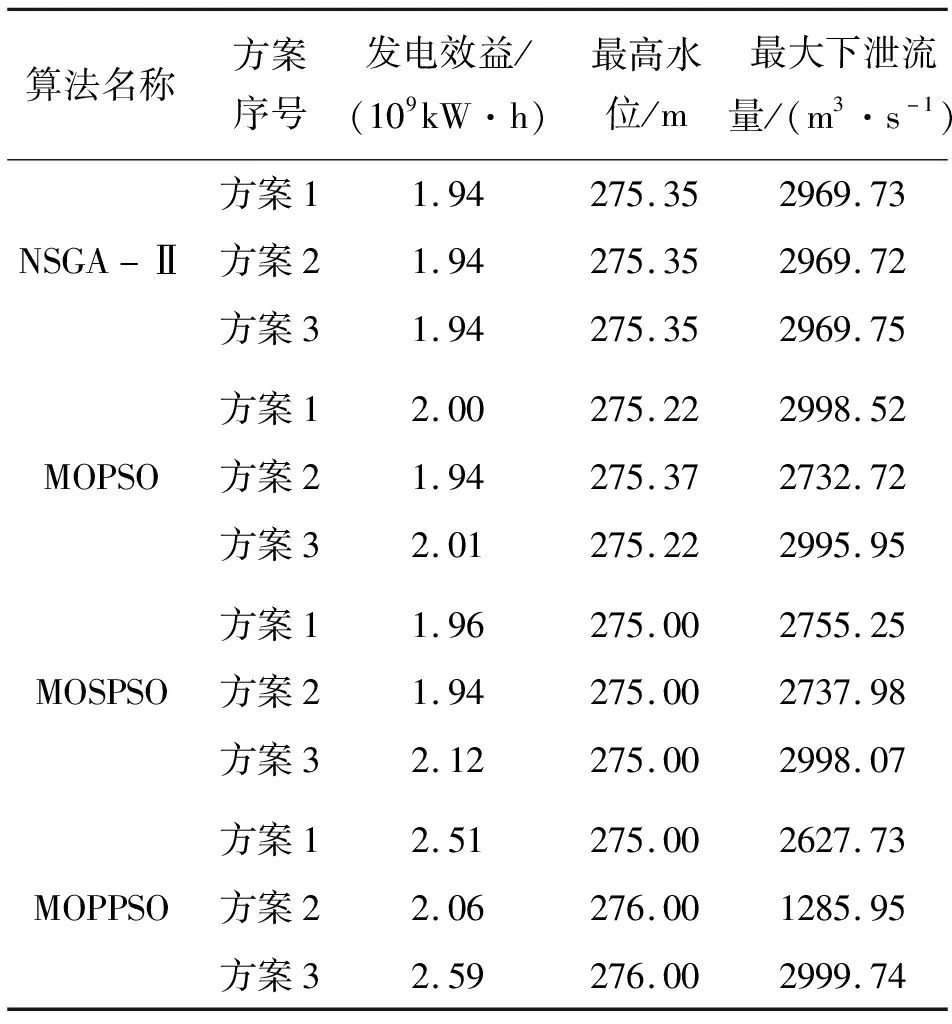
表4 各多目标算法的典型调度方案集

(2)从Pareto解搜索方面来看，MOPPSO算法较其他算法具有明显优势。除MOPPSO算法外，其余算法在Pareto解搜索问题上寻优效率低下。在3次计算中，NSGA-Ⅱ算法均在117 000代前因无进化趋势而停止进化，所得解集的超体积指标小，收敛性差，平均用时132 396.67 s；MOPSO算法在500 000代左右仍具有微弱的进化趋势，但解集距离真实Pareto前沿较远，超体积指标为2.34×1011，运行时间171 612.16 s，用时最长;MOSPSO算法在500 000代左右仍具有微弱的进化趋势，但解集距离真实Pareto前沿较远，超体积指标为5.49×1011，用时71 037.67 s，其解集的收敛性、分布均匀性、分布广泛性以及其运行时间都比NSGA-Ⅱ与MOPSO来的优秀。

从表3、4可以看出，在多次计算中，MOPPSO算法所得解集的发电效益最大目标的最优值的平均值达到了2.58×109kW·h，最高水位最小目标的最优值的平均值达到了275.00 m,最大下泄流量最小目标的最优值的平均值达到了1 243.09 m3/s，均远优于其他算法所得结果，其超体积指标为5.66×1012，远高于其他算法，可见MOPPSO算法所得解集较其他算法的解集更加接近真实Pareto前沿，且具有良好的收敛性、分布均匀性和分布广泛性；MOPPSO算法达到其Pareto前沿的平均运行时间55 548.33 s，运算效率优于其他算法。可以看出，MOPPSO算法在Pareto解搜索方面具有明显优势。

6 结 论

本文针对传统智能优化算法在高维的水库优化问题中寻优效率低下的原因，基于粒子群算法的框架，通过引入约束破坏向量、分段操作、特殊变异操作以及“分解聚合”策略等改进策略，提出了PPSO算法以及MOPPSO算法；通过实例的综合对比分析，证明了PPSO算法在时间步长较小、计算时段数目较多的水库调度可行解搜索方面具备极大的优势；证明了MOPPSO算法所得解集具有良好的收敛性、分布均匀性和分布广泛性，其运算效率具有明显优势。

相对其他的传统智能优化算法，本文提出的MOPPSO算法虽然具有所得解集的收敛性、分布均匀性、分布广泛性好以及运算效率高的优点，但其在Pareto解搜索阶段的运算时间仍然过长；除此之外，变异参数的设置的好坏会对其运算效率有一定的影响。所以亟待解决的问题是如何进一步提高其运算效率以及如何结合自适应算法以取得最佳的变异处理效果。