基于图像模糊度的极端天气实时检测方法
李晓勇,舒宇锋,卢 军,唐 陈,李红玉
(1.泸州市气象局,泸州 646000;2.成都信息工程大学,成都 610225;3.德阳市气象局,德阳 618000)
1 极端天气监测
传统的天气检测方法就是在各个城市周边地区设立相应的气象观测站,在气象观测站中放置空气温湿度传感器、大气压力传感器、监控摄像头等设备实时对当地区域的气象信息进行采集[1]。这种传统的天气检测方法可以准确采集到监测区域的气象信息,但是这对于其他没有设立气象观测站的地区就形成了“监测死角”;而在现实中,往往是将当地气象观测站采集的气象信息作为整个区域的气象标准,这对于特殊地区(高速公路,事故多发地等)的复杂天气就显得不够准确。
针对上述问题,国内外都提出了一些改进的方法,而这些方法都是需要增加新的传感器在监控系统上。如:谭永宏设计的嵌入式气象信息采集系统[2]、蒋方胜设计的基于ARM 的自动气象站系统[3]以及王柏林设计的随车移动式自动气象站[4]。虽然这些方法都在一定程度解决了气象观测站的成本大、需求土地资源大的问题,但是无法避免新增加硬件的损耗以及后期人员维护的管理问题。因此,找出一个在原设施基础上新的极端天气监测方法就显得至关重要。
2 图像模糊度与极端天气的关系实验
在出现极端天气的地区,通过监控器拍摄下来的图像是不一样的,在晴朗天气状况的城市(图1a)和高速公路(图1b),以及在浓雾天气状况下的城市(图1c)和高速公路(图1d)。


图1
由图像可以很直观地看出在不同的天气状况下,同一个地区的图像的清晰程度(可见度)[5]是不一样的,因此,可以判断图像的模糊度和极端天气是有联系的。图像的模糊度又可以理解为图像边缘的特征模糊,而检测图像的模糊度[6]就可以转换为图像的边缘检测。
2.1 Laplacian 算子
图像的边缘地区像素值会发生“突变”,而对于这些“突变”的区域进行求导时会看到极值的出现,如图2所示。而对其求二阶导数时就会发现“突变”区域会通过坐标系原点,也就是其二阶导数为0,如图3所示。因此,可以用这个特点开作为检测图像边缘的方法,即:Laplacian 算子。
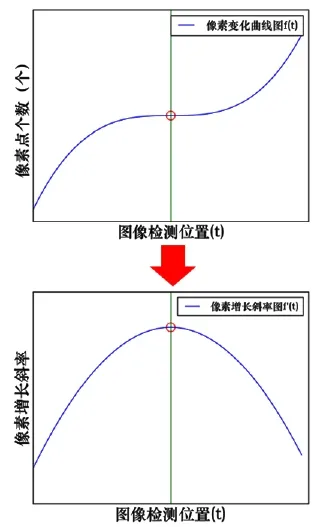
图2 “突变”区域极值图
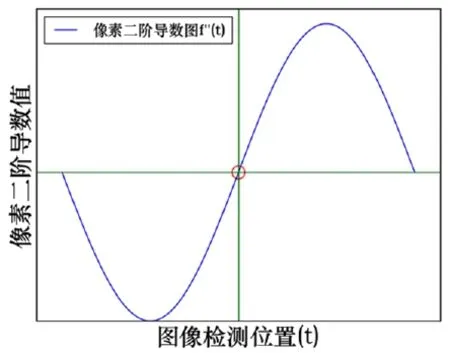
图3 “突变”区域二阶导数图
因为图像是“2维”的,需要在x和y两个方向进行求导,所以Laplacian 算子公式定义如下:
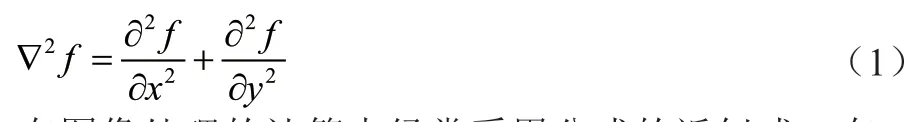
在图像处理的计算中经常采用公式的近似式,在x方向上为:
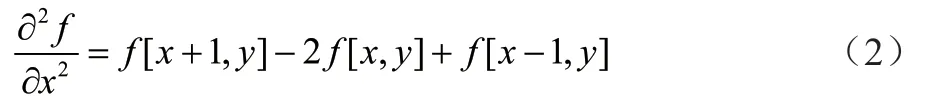
在y 方向上为:
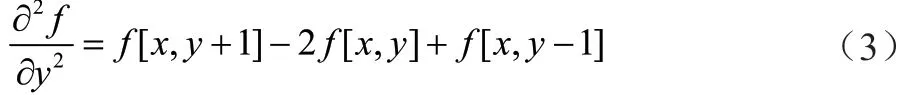
进一步可得出在x 与y 方向上的离散计算公式:
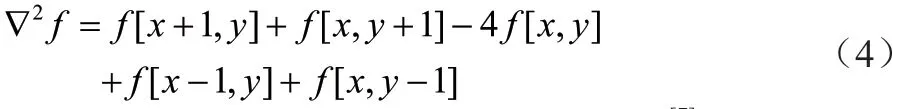
由于Laplacian 算子对噪声敏感度较高[7],因此,使用Laplacian 算子进行模糊度计算时通常需要在之前进行降噪处理,而经常使用的降噪方法为高斯滤波降噪。
2.2 高斯滤波
高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器,对于抑制服从正态分布的噪声非常有效[8]。对于图像来说,高斯滤波器是利用高斯核的一个2维的卷积算子,用于图像模糊化(去除细节和噪声)。由于图像是“2维”的,因此采用二维高斯分布公式:

高斯滤波后图像被平滑的程度取决于标准差。它的输出是领域像素的加权平均,同时离中心越近的像素权重越高。因此,相对于均值滤波(mean filter)的平滑效果更柔和,而且边缘保留的也更好。
2.3 LOG 算子实验
先将图像进行高斯滤波去除大部分噪声,然后将处理后的图像进行laplacian 算子计算,得出图像的模糊度值,这样的方法被称为高斯-拉普拉斯算子,简称为LOG 算子[9~11]。将图1a–图1d 使用LOG 算子进行计算,将模糊度标注在图像中,得到图4a’–图4d’。


图4
由图4a’和图4b’、图4c’和图4d’的对比可以看出在不同天气状况下相同场景的LOG 值是不一样的,晴朗天气下图像的LOG 值比雾天天气下的图像大,这是因为晴朗天气下的图像特征边缘多导致像素点之间的“突变”情况也多;而雾天天气下的图像特征边缘同化情况严重导致像素点之间的“突变”情况变少,所以Laplacian 值小。
2.4 气象数据实验
本实验使用四川省气象局提供的“绵竹市”气象观测站的监控数据以及雨量检测数据作为实验样本。并且取时间连续且有极端天气出现的白天数据:2018年6月25日早上9点至下午6点的降雨数据。如图5所示。
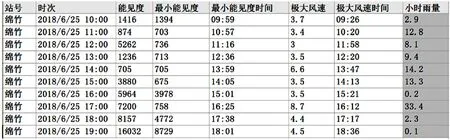
图5 绵竹降雨数据图
之后对视频使用FFmepg 进行截取为图像,本实验6秒截取一次,每分钟10张图像,并且取10张图像LOG值的均值作为每分钟的LOG 值。采用图像处理可以节省视频逐帧处理的时间浪费。最终将监控视频产生的图像LOG 值绘制为一条曲线与“绵竹市”雨量检测数据绘制的曲线放在一个坐标系中观察,如图6所示。由气象数据实验得到的实验结果图和理想的实验结果有差距,而产生差距的原因则是由监控摄像仪器的分辨率、刷新率以及其他非高斯噪声的影响,因此需要一个能够去除这些影响的新的算法。
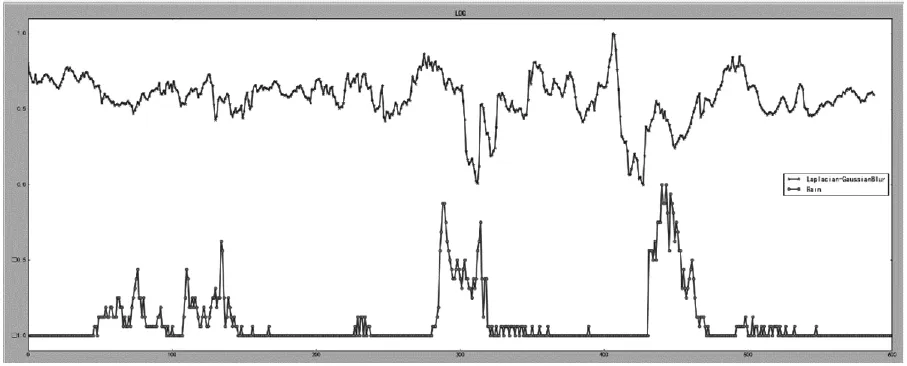
图6 实验结果图
3 图像模糊度的阈值去噪方法
3.1 Canny 算子的阈值思想
Canny 算子是一种多级检测算法,它其中的一个特点就是使用双阈值,即一个高阈值和一个低阈值来区分边缘像素,如果边缘像素点梯度值大于高阀值,则被认为是强边缘点。如果边缘梯度值小于高阀值,大于低阀值,则标记为弱边缘点,小于低阀值的点则被抑制掉[12]。而在本实验中由于噪声复杂因此采用设定一个LOG 值差作为一个阈值进行去噪处理,即前一个LOG 值和后一个LOG 值的差值绝对值,如果小于阈值K,那么就让前一个LOG 值等于后一个LOG 值;如果大于阈值K,那么就不作处理,公式如下:

由此公式处理可以最大程度消除非高斯噪声,将极端天气的LOG 值变化显示出来。
3.2 LOG 算法结合阈值K 去噪算法
根据上述思路,将阈值K 加入到LOG 算法中(以下简称K-LOG 算法),整体算法如下:
(1)将监控仪器视频用FFmpeg 进行分割为图像保存待使用。
(2)使用高斯滤波对图像进行第一次去噪,消除高斯噪声。
(3)使用Laplacian 算子对图像进行模糊度值计算。
(4)使用阈值K 去掉图像中的非高斯噪声。
(5)将最终的模糊度和雨量检测数据绘图进行对比。
(6)如果效果未达到预想,重复(4)。
4 实验结果分析
经过上述算法的计算得出新的实验结果如图7所示。经过多次实验算出此处监控摄像仪器的阈值K 为0.4。
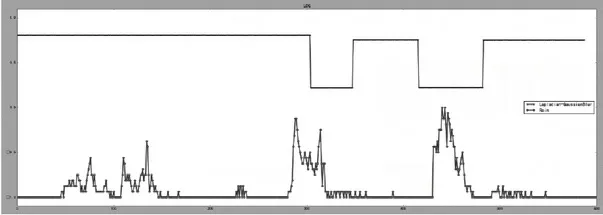
图7 K-LOG算法实验图
将计算出来的阈值K 用于新的监控时间中,实验结果如图8所示。
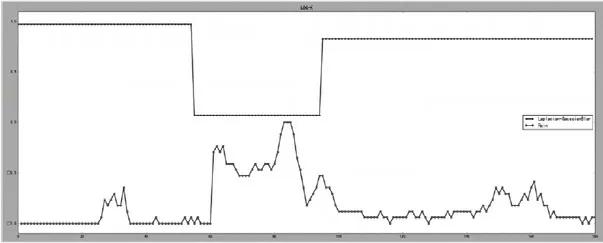
图8 K-LOG检测实验图
将LOG 算子与经过高斯滤波器处理的Canny 算子[13]用于实验对比,结果如图9与图10所示。
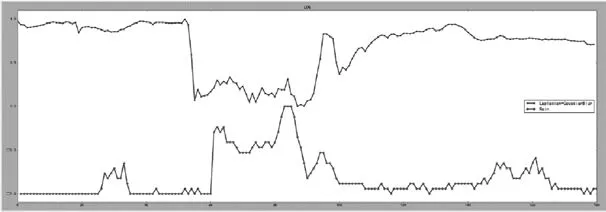
图9 LOG检测实验图
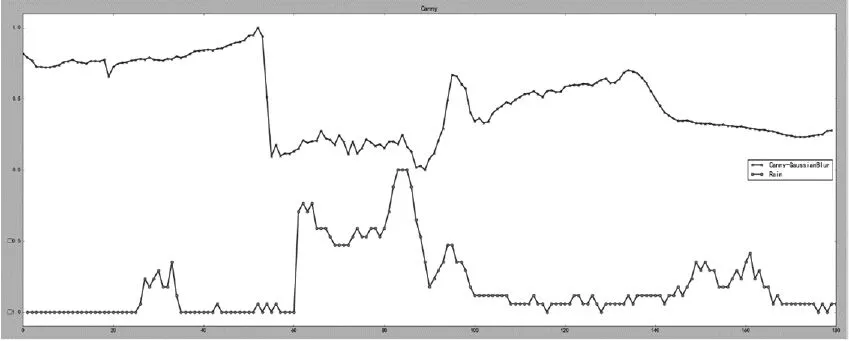
图10 Canny-Gaussian检测实验图
由实验可以得出在同一个监控摄像仪器拍摄相同环境、不同时间、不同气候都适用于同一个阈值K,这样经过训练出来的阈值K 就可以用于该环境的极端天气检测;并且比较图9和图10的实验结果可以发现,K-LOG算子的检测结果比原本的LOG 算子以及经过高斯滤波器处理的Canny 算子更加的精准和直观。
5 结束语
本方法只需要使用以往采集到的数据,加上机器学习算法找出适合当前监控摄像仪器的阈值K 就能在原有的设施上完成对极端天气的检测,这个方法增加了对特定区域的极端天气检测的精确度,遍布的监控摄像仪器也降低了新增加设备的财力消耗和人力资源浪费的情况。在实际应用中只需要将算法的阈值K 用于监控摄像仪器的视频流数据就可以做到对极端天气的实时检测。

