螺纹综合测量机的扫描原理与误差分析
张和君,欧协锋,马俊杰
(深圳市中图仪器股份有限公司,广东深圳518071)
0 引言
螺纹是一个复杂的空间曲面体,它由许多几何参数构成,如中径(中径、单一中径、作用中径)、大径、小径、螺距(导程)、牙型角、牙侧角等。螺纹具有连接、传动和密封等作用,其制造精度直接影响连接可靠性、装配精度、互换性和密封性能等。因此,需对螺纹参数进行严格的检测分析,以减少不合格螺纹的使用,预防失效。目前,测长机应用三针法检测外螺纹,量球法检测内螺纹和外螺纹,检测得到螺纹的单一中径。三针法、量球法检测螺纹的单一中径是一种经典传统方法,适用于精度高、种类多、单件或小批量生产的螺纹量规的检验与测试。
随着高精度导轨技术、高精密加工技术、高精密光栅技术和智能化软件等关键技术的成熟应用,出现了一种创新性的螺纹参数检测技术——接触式二维轮廓扫描技术,即利用高精度的螺纹综合测量机[1](简称螺纹机)进行螺纹检测。该技术颠覆了传统的螺纹检测方法,突破性地解决了螺纹综合参数检测的问题,真实地综合反映螺纹参数的各项性能指标。本文介绍螺纹综合测量机扫描检测圆柱螺纹的原理和特点,分析检测方法中的误差影响要素,并进行不确定分析。
1 螺纹综合测量机的工作原理
1.1 螺纹机检测螺纹的工作原理
螺纹机类似二维坐标扫描测量仪,采用接触扫描式检测原理,具有方法简单、测量精度高、工作效率高、综合成本低、测量结果全面等优点,是螺纹综合参数测量的最好方案,其构造如图1所示。
螺纹机利用牙顶自定心夹具[2](外螺纹使用V型面夹具,内螺纹使用两刀口夹具,见图2)对螺纹进行定位,保证螺纹的轴截面与扫描针的运动平面重合,其工作原理如图3所示。
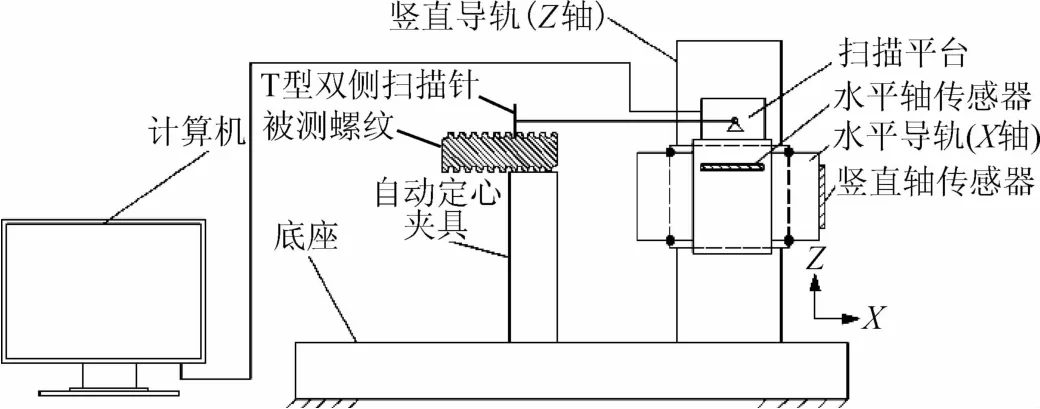
图1 螺纹机构造图
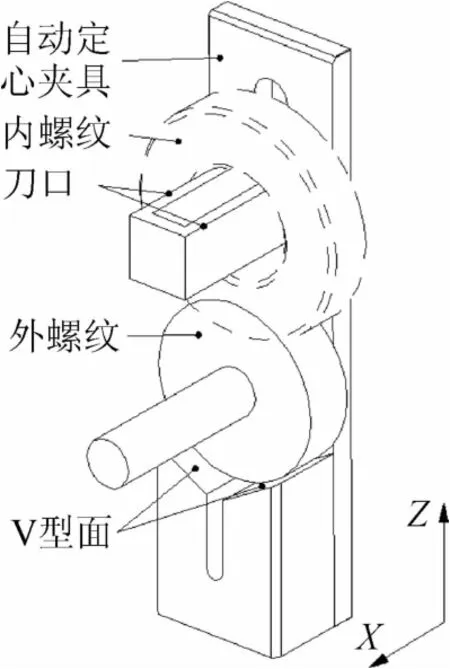
图2 自动定心夹具
测量时,扫描针分别对螺纹轴截面上、下两侧的螺纹轴向轮廓进行接触扫描,以高分辨力(不大于0.01μm)、海量“点云”数据(不小于5000点/秒)采集扫描针的轨迹,完成螺纹轴截面轮廓的数据采集,获得螺纹的轴向轮廓。
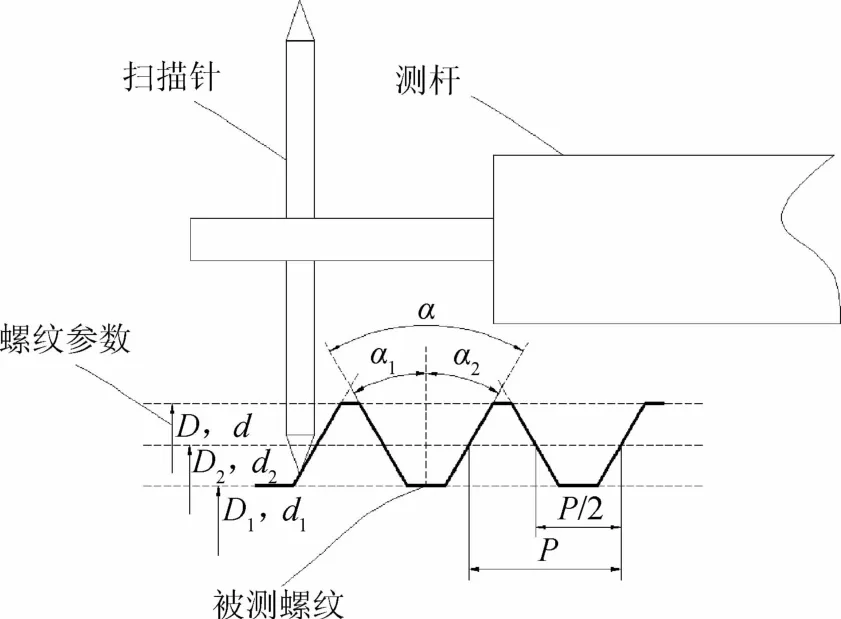
图3 螺纹机的工作原理
扫描得出的螺纹轮廓曲线为
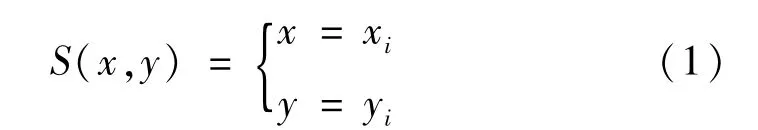
式中:xi和yi分别由水平轴和竖直轴传感器获得。
1.2 螺纹轮廓扫描曲线的针尖补偿建模
螺纹机通过传感器系统初步得到的轮廓是扫描针针尖球心点的坐标,因扫描针针尖半径和螺旋升角的存在,当螺纹轴向截面上滑行时,扫描针针尖与螺纹表面的接触点并不在轴向截面上,而是与螺纹轴向之间存在偏移。因此,得到扫描针针尖球心点的坐标后,还需进行螺旋升角和针尖半径的修正,才能真正获得被测螺纹的实际轮廓曲线。下面以外螺纹为例讨论,内螺纹同理。
1)检测外螺纹的空间几何模型
图4(a)为螺纹轴向截面图,当前扫描针针尖距离螺纹轴线的高度位置为A。以螺纹轴线为Z轴,当前扫描针针尖球心O′与螺纹轴线的交点为坐标原点O,扫描针针尖球心垂直向上方向为X轴,垂直XOZ平面向外为Y轴。扫描针针尖半径为R。
2)螺纹螺旋面方程
螺纹左右侧面由一组阿基米德螺旋线组成,螺纹左右侧面sp和qt的表达式分别为
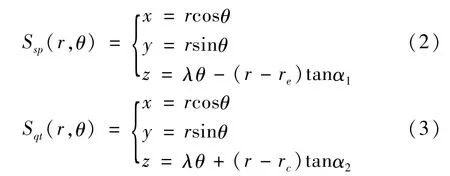
式中:λ=P/2π为螺旋参数,是动点绕螺纹轴线转动单位弧度沿螺纹轴线所移动的距离。当λ=0时,式(2)和式(3)表示V型圆环槽的两侧圆锥面;当r为常数时,S(θ)表示的是一条螺旋线;当θ为常数时,S(r)表示的是轴向截面的一条直线。
图4(b)中,曲面Ssp和Sqt与扫描针针尖的接触点分别为a和b,接触点与扫描针针尖球心的连线方向为曲面S(r,θ)的表面法向量的方向。对于曲面参数方程S(r,θ),在任意一点(r,θ)上的法向量为
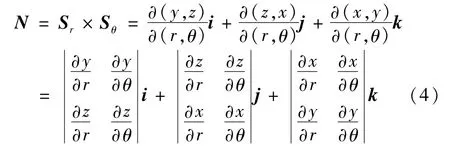
式中:i,j,k分别为直角坐标系x,y,z轴的单位向量。
对于螺纹左、右侧面,任意一点的法向量为[3]
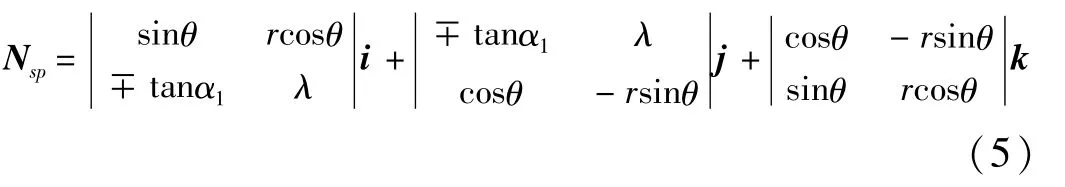
单位法向量为
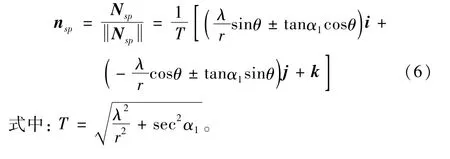
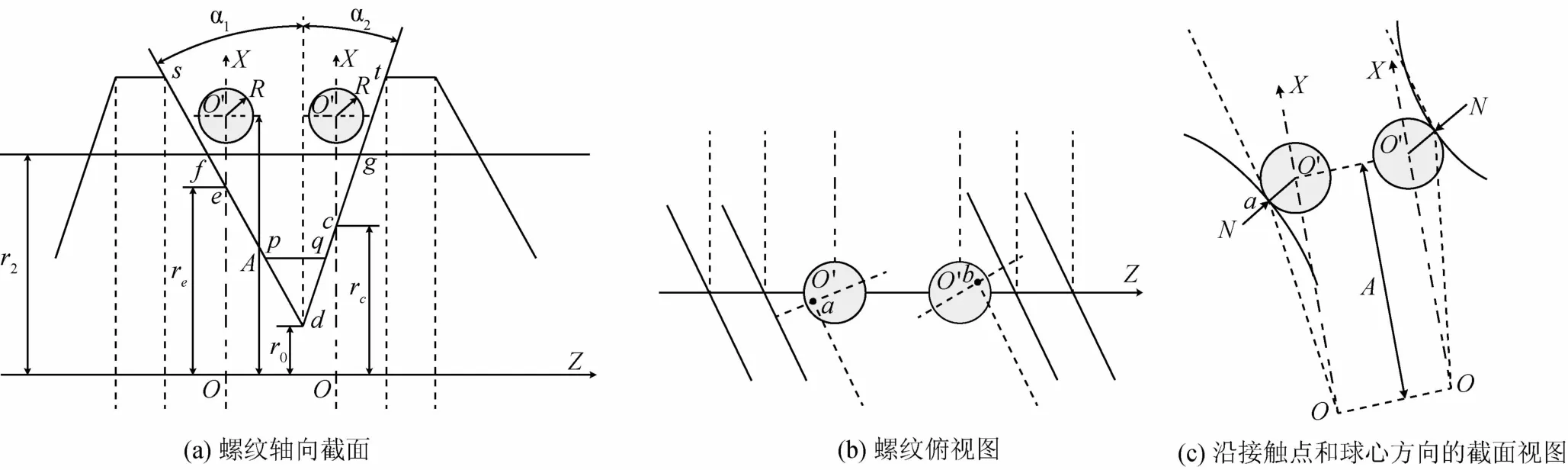
图4 接触法测量外螺纹的模型
3)接触点坐标计算
为计算螺纹左侧面sp上的接触点坐标(r,θ),考虑空间三角形OaO′中的矢量关系为
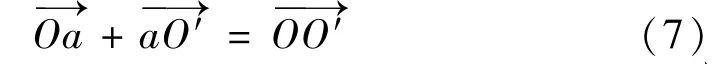
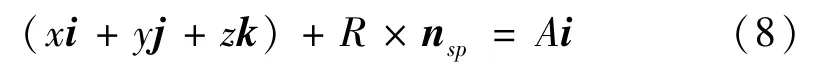
即
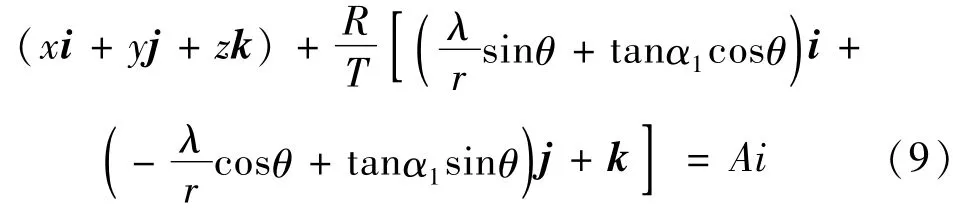
由式(9)得
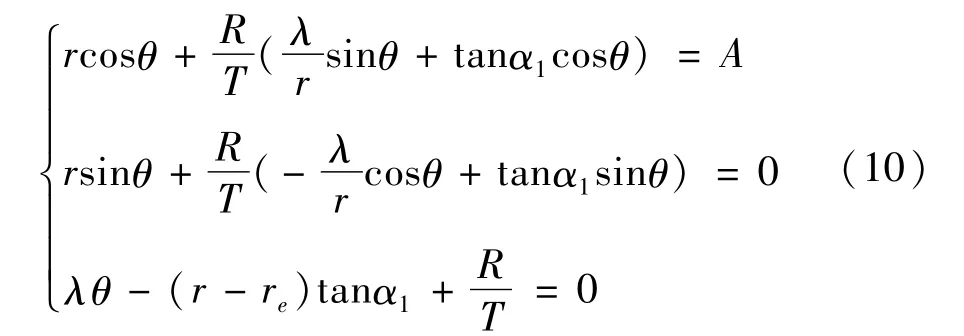
由式(10)可得
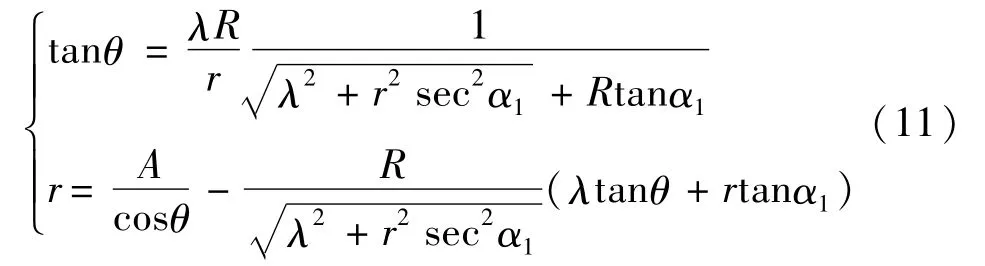
当扫描针针尖半径R、牙型半角α1、螺距P已知,给定球心高度位置A,即可由式(11)求出两个未知数r和θ,从而得到测球的接触点坐标。式(11)两个方程为超越方程,可由迭代方式求出未知数。
同理可计算螺纹右侧面qt上的接触点坐标(r,θ)
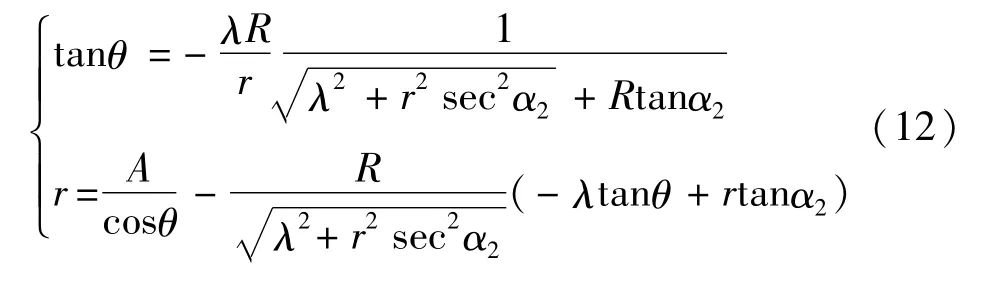
4)螺旋升角修正和针尖半径补偿
对扫描针针尖的每一个扫描位置A,都需要求出接触点位置(r,θ),进而得到真正的螺纹轴向截面左右侧的位置点m和n,同时自然地包含了半径修正。如图5所示,通过修正得到一个虚拟的,且更大测针半径R′。由式(11)和式(12)得曲面sp上的虚拟针尖半径为
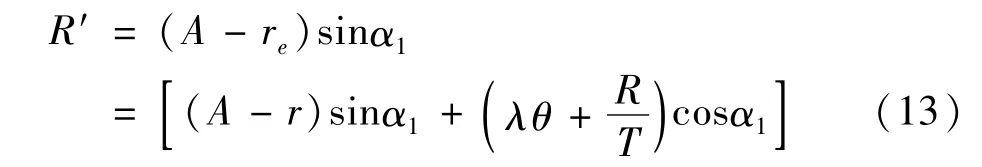
曲面qt上的虚拟针尖半径
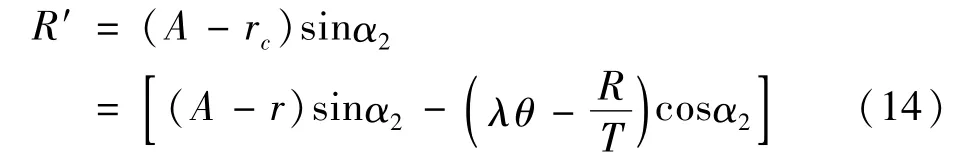
对扫描针针尖的每一个扫描位置(xo′,zo′),求出接触点位置(r,θ),从而得到经过升角修正和针尖半径补偿的截面位置点m和n的坐标分别为
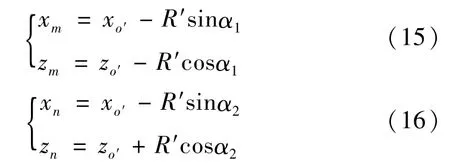

图5 螺旋升角的修正模型
对于外螺纹,在曲面sp上,接触点的螺旋角θ>0°;在曲面qt上,接触点的螺纹角θ<0°。当λ=0°时,螺纹退化成一个V型圆环槽,此时螺旋角θ=0°。若不经过修正,直接将接触点位置(r,θ)当做轴向截面位置,则对于中径和牙型角的计算会引入误差,会将牙侧面抬高一个位置,增大值

对于每个扫描位置,针尖虚拟半径R'都是不同的。当牙型半角左右对称即α1=α2=α时,对中径测量的影响将会增大
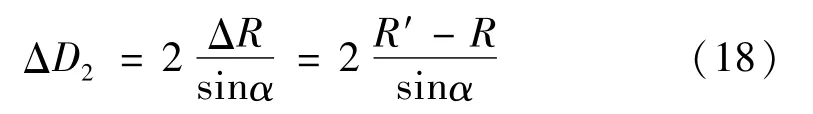
1.3 螺纹扫描位置计算
由于扫描点数据较多,虽然可以离线计算,但是对每个扫描位置进行迭代求解则计算量仍然较大。可以事先计算出一张四维查找表(R,α1,P,A)~(r,θ),便于进行求解。根据截面度要求,可适当缩小查找表的规模,查表时使用插值计算。
通过建立螺纹轴线为Z轴,可以将扫描数据从机器坐标系规范到螺纹工件坐标系,得到测球中心距离轴线的所有扫描位置A。
由于扫描时牙型半角α1并不是已知的,且螺纹轴线方向也需要经测量得出,因此,在计算时先设定一个标称值的初始牙型半角,以及由牙顶或者牙底拟合计算的初始螺纹轴线,通过式(11)计算出真正的螺纹轴向截面,进而计算出螺纹轴线和牙型角;然后利用计算出的螺纹轴线将扫描数据再次规范,将牙型角再次代入式(11)计算新的螺纹轴向截面,依次循环进行迭代计算,直到满足要求为止。
1.4 螺纹综合参数计算
螺纹轮廓扫描、计算完成后,系统根据螺纹参数的定义直接进行分析、拟合、计算,获得中径(基本中径、单一中径、作用中径)、大径、小径、螺距R(导程)、牙型角α、牙侧角、牙侧直线度D等参数,见图6。同时根据螺纹标准数据库,自动对螺纹参数的检测结果进行合格性判定,整个测量过程全自动完成,仅需2 min。
螺纹机的测量原理符合GB/T 28703-2012《圆柱螺纹检测方法》和JJF 1345-2012《圆柱螺纹量规校准规范》的要求[5-6],结果完全符合螺纹参数的定义。结果包含每个牙的独立参数,能够真实地综合反映螺纹参数的各项性能指标。
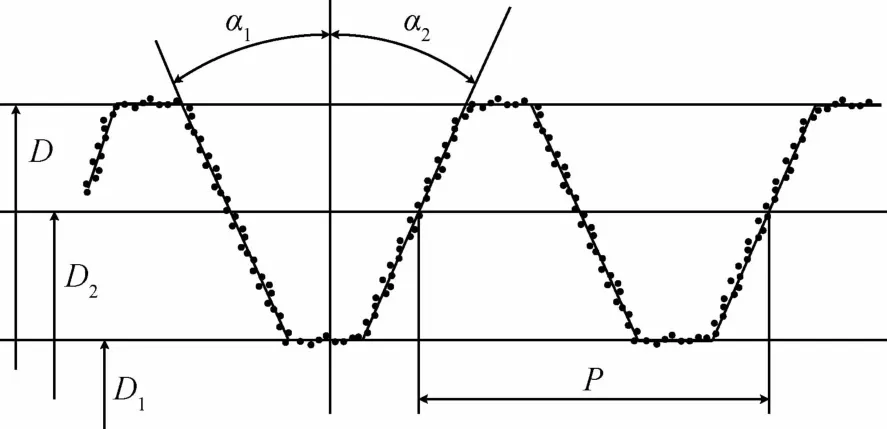
图6 螺纹参数的拟合计算
2 螺纹综合测量机的误差分析
牙顶自定心夹具、极小半径(10~30μm)的扫描针针尖的应用保证了螺纹轴向截面轮廓的采集准确性,没有类似测长机的万能工作台(需要找拐点)和多种修正参数等繁琐的结构和修正算法,提高了操作便利性。直接根据螺纹参数的定义计算螺纹参数,完全符合螺纹参数的定义。螺纹机是一台复杂的高精密仪器,其测量准确度与仪器的结构原理、数据处理、测量环境等相关,具体因素包含环境温度、光面标定规的准确度、测量力引起的变形、扫描针针尖半径误差、被测件安装偏差、传感器的误差、数据处理算法误差、二维导轨的误差、斜置误差等。为提升仪器的综合测量准确度,这些误差因素在仪器设计和装配制造时必须予以补偿修正或者控制。表1给出了螺纹综合测量机的主要误差项及其控制方法。
由表1分析可知,在操作使用方面,螺纹综合测量机的误差主要来源于长时间工作时温度变化引起的误差、光面规的校准误差和扫描针针尖的半径误差等。因此,在使用时需要注意:①严控校准室的环境温度,使用一段时间后使用光面规对仪器重新进行标定;②采用二等以上的光面规为仪器校准;③扫描针针尖较细,需要注意保护,尽量减少磨损。
目前,检测圆柱螺纹的传统方法是测长机的三针法及量球法,新型的轮廓扫描法近几年也迅猛发展起来。这两种检测方法的测量结果存在一些差异,其中三针法只能检测检测螺纹的单一中径,优点是测量的原理几何模型简单,存在历史悠久,在不进行误差修正的前提下检测单一中径速度快。表2给出了传统三针法与轮廓扫描法测量螺纹的误差影响因素比较分析[6-7]。

表1 螺纹综合测量机的误差分析与控制

表2 传统三针法与轮廓扫描法测量螺纹的误差影响因素比较
由表2可知,传统三针法测量螺纹中径的结果需修正多项误差,若不修正,将引入较大的测量误差;另外,若螺纹量规圆度及圆柱度不好(如椭圆形)或者牙侧直线度不好,量针与螺纹规的不同接触点也将测得不同值。轮廓扫描法采用极小半径的扫描针尖对螺纹轴截面上的牙型轮廓进行接触扫描,得到轴截面的上下两条螺牙轮廓曲线,然后进行分段几何拟合计算。相比三针法利用的少数接触点信息,轮廓扫描的每条曲线含有多达数十万个数据点,更能全面反应牙型轮廓,测量参数结果也能综合反映多个螺牙的情况。因此,轮廓扫描法对螺纹参数的评价具有更明显的优势。
3 结论
随着对螺纹参数重要性认识的不断提高,传统的检测方式已不能完全满足现代工业化水平所要求的全面、准确、高效的检测需求。完整再现螺纹的实际情况,以螺纹综合状态作为判定依据,才能使螺纹的质量得到保证[8]。提高螺纹检测水平是提高螺纹制造质量的基础和动力。
用来检测圆柱螺纹单一中径的三针、量球法是一种简单、传统的测量方法,目前在国内外仍有广泛市场。但该方法因其测量原理的制约,经传统测量误差来源[9-10]所得误差分量均比较大,且存在人为操作等不确定因素,需要经过修正才能得到准确测量结果。
螺纹综合测量机是螺纹测量的新兴技术仪器,采用的接触扫描法具有精度高、速度快、参数全面、检测过程全自动化、人为影响小等优点,能真实、全面地反映各个参数对螺纹性能的综合影响,是测量螺纹综合参数的优选方案。螺纹参数的综合检测是实现螺纹量值溯源的技术要求,螺纹综合参数的准确测量是实现螺纹量值溯源的基础。

