基于P?V曲线法的光伏电源系统电压稳定性分析

闫群民 申卓群 马永翔 陈昊睿

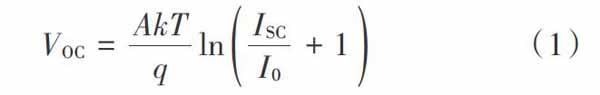
摘  要： 光伏发电由于其受外部环境因素影响，其输出功率不确定性较大，接入电网后易导致电力系统电压产生波动甚至越限。该文提出基于P?V曲线的光伏电源系统电压稳定性分析方法，阐述光伏电源输出特性及P?V曲线法分析原理，基于PSASP软件仿真平台建立含分布式光伏电源的IEEE 13节点模型。以极限功率参数和电压临界稳定值为考核指标，分析了不同渗透率、接入方式下对系统电压稳定的分布情况。分析结果表明，P?V曲线法可以有效反映出系统稳定性最薄弱区域，并利用仿真结果提出了工程应用分析，对含光伏分布式电源系统电压稳定性分析有一定的借鉴意义。

关键词： 电压稳定性分析; 光伏电源; P?V曲线法; IEEE 13节点建模; 仿真实验; 工程应用分析

中图分类号： TN86?34                              文献标识码： A                       文章編号： 1004?373X（2020）06?0110?05

Analysis of voltage stability of photovoltaic power system based on P?V curve method

YAN Qunmin， SHEN Zhuoqun， MA Yongxiang， CHEN Haorui

（School of Electrical Engineering， Shaanxi University of Technology， Hanzhong 723000， China）

Abstract： As the influence of external environmental factors， the output power of photovoltaic power generation is highly uncertain， which may easily lead to voltage fluctuation or even exceed limit in the power system when connected to the power grid. A method of the voltage stability analysis of photovoltaic power system based on P?V curve is proposed. The output characteristics of photovoltaic power and the analysis principle of P?V curve method are expounded. The IEEE 13?node model with distributed photovoltaic power is established based on PSASP software simulation platform. The distribution of voltage stability under different permeability and access modes is analyzed by taking the limit power parameters and the critical stability value of voltage as the evaluation indexes. The analysis results show that the P?V curve method can effectively reflect the weakest area of system stability， and the engineering application analysis is proposed with the simulation results. It has certain reference significance for the voltage stability analysis of the distributed photovoltaic power system.

Keywords： voltage stability analysis; photovoltaic power; P?V curve method; IEEE 13 node modeling; simulation experiment; engineering application analysis

随着分布式光伏电源技术的日益成熟，其应用规模及范围也将进一步扩大，同时其对传统电网也带来了更多的挑战。光伏发电由于其出力受外界环境约束因素较多，导致其在电网中具有很强的不确定性，而电网运行的一项核心指标就是运行工况的稳定性，如何使含有分布式光伏电源的电力系统更加稳定可靠运行，正是国内外许多专家学者的研究热点[1?5]。

目前，分布式光伏电源接入对电网电压影响已有一定的研究成果。文献[6]研究了广义负载功率波动、功率因数、接入配电网电压等级对电压波动影响。文献[7]推导了分布式光伏电源若干种典型分布情况下线路电压偏差和电压波动不越限时所能允许接入的极端容量极限。文献[8]研究了电网静态分析中的常用指标，并在此基础上考虑了多种因素对配电网静态电压稳定性的影响。文献[9]研究了在满足电压限制条件下最大光伏接入容量，并提出解决高渗透率分布式光伏发电接入所引起电压越限的措施和方案。

本文基于PSASP仿真软件，建立了含分布式光伏电源的IEEE 13节点仿真模型，提出P?V曲线法仿真分析了系统电压稳定性，以极限功率參数和电压临界稳定值为量化考核指标，得出不同接入方式及不同渗透率对系统电压的具体影响。

1  P?V曲线法分析

分布式光伏电源出力直接受外部环境影响，其主要影响因素为太阳光光照强度和光伏电源所在环境温度。设太阳能电池板短路电流为ISC，可得其开路电压：

式中：A为电池片二极管常数;k为玻尔兹曼常数;T为开尔文温度;q表示单位电荷电量;ISC为短路电流;I0为反向饱和电流。

由短路电流和开路电压可得光伏电池输出功率：

式中，[FF]为填充因子。

由式（1）、式（2）可得出分布式光伏电源出力受外部环境影响较为明显，当外部温度和光照强度发生较大变化时，光伏电源出力将不可控，对电网稳定性产生负面影响。

本文结合目前分布式光伏电源接入位置和容量的已有研究成果，提出以[FF]曲线法对电压稳定性进行分析研究。[FF]曲线分析方法的具体原理如图1所示。设坐标零点为原始运行点，x轴为负荷，y轴为电压。在低水平的负荷条件下，对应一个负荷值，系统有两个平衡解：一个为高电压解UH;另一个为低电压解UL。高电压解对应着低传输电流，低电压解对应着高传输电流。当负荷逐渐增加时，负荷节点的电压会逐渐降低。同时，两个平衡解会逐渐靠近并最终在Saddle Node Bifurcation（电压崩溃点）处重合。如果负荷再进一步增加，系统将没有平衡解，即平衡解在SNB处消失。点SNB处为鞍结分岔，系统发生电压崩溃。从初始运行点到崩溃点（SNB）的距离λ称之为负荷裕度。负荷裕度目前被认为是最有效的电压稳定评估指标，它反映了系统对负荷的承受能力[10]。

从以上分析得：曲线上半部为稳定运行区域，下半部为不稳定运行区域;高电压解UH为静态稳定的平衡点，低电压解UL为静态不稳定的平衡点 。

2  含分布式光伏电源的系统建模

本文采用IEEE 13标准节点系统，通过在不同位置增加不同出力的分布式光伏电源，以达到建立一个可以模拟不同渗透率下节点电压变化的模型。IEEE 13节点系统拓扑结构如图2所示。

系统建模数据选取时为了突出不同接入位置和渗透率对节点电压的影响，采取单一变量控制法，将各节点的负荷和线损进行理想化统一，各节点负荷均设置为有功功率0.09 MW、无功功率0.08 Mvar，节点额定电压10 kV取为电压基准值，电网接入节点1并取其额定容量100 MV·A为功率基准值，线损均设置为线路正序电阻3.3 Ω、线路正序电抗3.6 Ω。系统网络共计12处负荷，总负荷为1.08 MW+0.96 Mvar，线路损耗一共11处，总损耗为正序电阻36.3 Ω，正序电抗39.6 Ω。

3  分布式光伏发电接入对电压的影响分析

利用图2建立的IEEE 13节点模型和参数对不同情况下的分布式光伏发电接入进行仿真与分析。

3.1  未接入分布式光伏发电的情况

利用PSASP仿真软件，对未接入分布式电源的IEEE 13节点系统进行分析。系统运行时，节点电压与功率变化越大，对系统稳定性威胁就越大。对各节点曲线图进行比较后，选取具有代表性的4，9，10，12节点作为分析对象，其P?V曲线如图3所示。

由图3可知，节点4由于较为靠近电源点，其负荷节点电压随着节点负荷的增大降低幅度较其他节点偏小;节点12由于距离电源点距离最远，其负荷节点电压随着节点负荷的增大，降低的幅度也是最大的。系统临界稳定点即电压崩溃点的极限功率参数为0.001 9 p.u.，此时负荷再进一步增大，系统将没有平衡解，系统发生电压崩溃。当节点负荷达到最大值时，4，9，10，12节点的电压临界稳定值分别为0.729 p.u.，0.548 p.u.，0.497 p.u.，0.436 p.u.。综上可知，12节点为该系统稳定性最薄弱的母线。

3.2  接入分布式光伏发电的情况

本节分别从接入位置和渗透率两方面对接入分布式光伏电源的IEEE 13节点系统进行分析。此处采用的渗透率定义为：所有PV单元发出的有功功率之和与系统总负荷的有功需求之比。

[PV渗透率=PPVPL×100%]

运用PSASP软件，在不同的节点加入相同功率的分布式光伏电源，并对系统进行了潮流计算和电压稳定性分析，得到各节点相关数据，并得到其P?V曲线图。

3.2.1  同一渗透率下接入方式对系统电压稳定分析

设渗透率为10%即接入总功率为0.11 MW，无功功率为0.1 Mvar的分布式光伏电源，该渗透率下的PV输出以不同的接入方式接入到系统中，以观察其对系统电压的影响。接入方式分别选择均匀接入、首端接入和末端接入。

1） 均匀接入。渗透率为10%均匀接入，各节点均接0.9×10-2 MW+0.8×10-2 Mvar的分布式光伏电源，同样选取具有代表性的4， 9， 10， 12节点作为分析对象，其P?V曲线图如图4所示。

由图4可以看出，4，9，10，12节点系统临界稳定点即电压崩溃点的极限功率参数依然为0.001 9 p.u.，此时负荷再进一步增大，系统将没有平衡解，系统发生电压崩溃。当节点负荷达到最大值时，4，9，10，12节点的电压临界稳定值分别为0.735 p.u.，0.559 p.u.，0.509 p.u.，0.443 p.u.。相较于图3而言，各节点的电压临界稳定值均提升但不明显，最薄弱母线依然为12节点。

2） 首端接入。渗透率为10%选择首端接入时，在节点4接入0.11 MW+0.1 Mvar的分布式光伏电源。因为节点4本身负荷仅为有功功率0.09 MW、无功功率0.08 Mvar，则节点4会将多余功率输出给其他节点，故节点4 P?V曲线图如图5所示。

其他9，10，12三个节点P?V曲线图如图6所示。

由图5、图6可以看出，9，10，12节点系统临界稳定点即电压崩溃点的极限功率参数依然為0.001 9 p.u.，此时负荷再进一步增大，系统将没有平衡解，系统发生电压崩溃。当节点负荷达到最大值时，4，9，10，12节点的电压临界稳定值分别为0.746 p.u.，0.563 p.u.，0.511 p.u.，0.450 p.u.。相较于图4而言，各节点的电压临界稳定值基本不变，最薄弱母线依然为12节点。节点4因为接入分布式光伏电源的功率大于本身负荷功率，故其P?V曲线图在负半轴上。

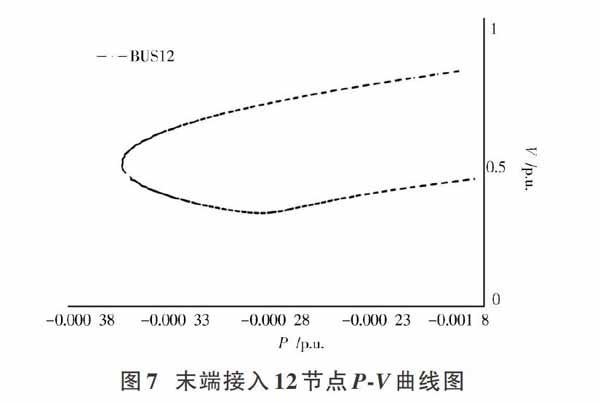
3） 末端接入。渗透率为10%选择末端接入时，在节点12接入0.11 MW+0.1 Mvar的分布式光伏电源。与首端接入节点4一样，因为节点12本身负荷仅为有功功率0.09 MW、无功功率0.08 Mvar，则节点12会将多余功率输出给其他节点。节点12 P?V曲线图如图7所示。其他4， 9， 10三个节点P?V曲线图如图8所示。

由图7、图8可以看出，4，9，10节点系统临界稳定点即电压崩溃点的极限功率参数上升到了0.002 23 p.u.，此时负荷再进一步增大，系统将没有平衡解，系统发生电压崩溃。当节点负荷达到最大值时，4，9，10，12节点的电压临界稳定值分别为0.715 p.u.，0.538 p.u.，0.475 p.u.，0.486 p.u.。相较于图4而言，前3个节点的电压临界稳定值稍有下降，但节点12临界稳定值上升，最薄弱母线变为节点10。综上，分布式光伏电源接入方式选为末端接入时，对最薄弱母线电压稳定性提高效果较为明显。

3.2.2  同一渗透率下不同接入方式的情况分析

在确定末端接入方式对最薄弱母线电压稳定性提高最有效之后，本文选取不同的渗透率，全部采用末端接入的方式，以比较渗透率变化对电压稳定性的影响。需要注意的是在渗透率大于10%时，只要全部在同一节点接入即在节点接入0.11 MW+0.1 Mvar的分布式光伏电源。由于本系统任一节点本身负荷仅为有功功率0.09 MW、无功功率0.08 Mvar，则该节点会将多余功率输出给其他节点，故该节点P?V曲线图将出现在负半轴。

分别选取25%，35%，45%，55%四种不同的渗透率，接入节点均选在节点12，其P?V曲线仿真结果如图9所示。

由图9可以看出，随着接入分布式光伏电源渗透率的逐渐增加，末端节点的电压临界稳定值也逐渐上升，且裕度也逐渐增大。其他节点电压变化情况如表1所示。

由表1可知，随着渗透率的逐渐增加，各节点的电压也随之增大，并且越靠近分布式光伏电源，附近节点的电压提升效果越明显。平均渗透率每增加10%，接入节点电压上升0.03 kV。其余节点电压上升幅度随着与接入节点距离的增加而减小。如果渗透率继续加大，节点12电压可能出现越上限的情况。因此，须合理配置分布式光伏电源接入渗透率，使有增压需求的节点电压合理上升，且避免出现因渗透率过高使电网电压失稳的情况出现。

由仿真结果可知，在实际工况下当辐射状网络末梢母线出现电压越下限时，应在电压越下限母线就近接入分布式光伏电源，以对该母线电压产生支撑作用，其接入容量应满足使该母线电压在满负荷运行时电压下限满足国家运行标准。若分布式光伏电源接入容量过大，则会使该母线电压越上限，此时需要在分布式光伏电源上配置电源监控模块和谐波分析控制模块以便在电源出力过大时进行调节，避免电压越上限造成用户用电设施损坏产生安全隐患。

当该母线在低负荷运行时，若分布式光伏电源出力大于该母线负荷，则会由该母线产生将多余出力输入电网产生反向功率影响电网稳定。此时需要在该母线加入消纳措施，如配置分布式储能装置和自动投切的电容器组，及时就地消化储存多余出力避免功率反送。

4  结  语

本文以PSASP电力系统仿真软件作为仿真平台，运用P?V曲线法分析了光伏电源接入方式，由于渗透率不同对电网电压质量的影响，得出了以下结论：

1） P?V曲线法可以有效反映出系统各节点电压稳定性，分布式光伏电源的接入有利于电网电压的提升，增大系统电压临界稳定值，从而改善电网电压的静态稳定性。

2） 分布式光伏电源的不同接入方式对电网电压的提升效果不同。在渗透率一定的情况下，当分布式光伏电源接入方式为系统末端接入时，对系统中最薄弱母线电压稳定性提高效果最为明显。

3） 分布式光伏电源的接入渗透率越大，电网电压的提升效果越明显，平均渗透率每增加10%，接入节点电压上升0.03 kV。其余节点电压上升幅度随着与接入节点距离的增加而减小。同时，当渗透率大于55%时，接入节点的电压会越上限导致电压不稳，从而导致系统电压失稳。

4） 实际工况中分布式光伏电源接入时应考虑到实际情况，对电压越限和反向潮流等问题采取相应措施，如增强电源控制增加储能装置等，保证用户用电质量和电网运行稳定。

参考文献

[1] 许正梅，梁志瑞，苏海峰.分布式光伏电源对配电网电压的影响与改善[J].电力自动化设备，2011，27（10）：1?5.

[2] 陈炜，艾欣，吴涛，等.光伏并网发电系统对电网的影响研究综述[J].电力科学与工程，2013，33（2）：26?32.

[3] 沈鑫，曹敏.分布式电源并网对于配电网的影响研究[J].电工技术学报，2015，30（z1）：346?351.

[4] 庄慧敏，巨辉，肖建.高渗透率逆变型分布式发电对电力系统暂态稳定和电压稳定的影响[J].电力系统保护与控制，2014，42（17）：84?89.

[5] 李蕊，李跃，郭威，等.分布式电源接入对配电网可靠性影响的仿真分析[J].电网技术，2016，40（7）：2016?2022.

[6] 陈权，李令冬，王群京，等.光伏发电并网系统的仿真建模及对配电网电压稳定性影响[J].电工技术学报，2013，28（3）：241?247.

[7] 黄炜，刘健魏，昊焜，等.分布式光伏电源极端可接入容量极限研究[J].电力系统保护与控制，2015，43（3）：22?28.

[8] 陈海焱，段献忠，陈金富.分布式发电对配网静态电压稳定性的影响[J].电网技术，2006，30（19）：27?30.

[9] 王颖，文福铨，赵波，等.高密度分布式光伏接入下电压越限问题的分析与对策[J].中国电机工程学报，2016，36（5）：1200?1207.

[10] 刘天琪，邱晓燕，李华强.现代电力系统分析理论与方法[M].北京：中国电力出版社，2016.