一种基于三维视觉的移动机器人定位与建图方法

陈超 张伟伟 徐军

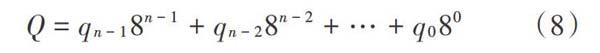
摘  要： 针对移动机器人三维视觉SLAM（同步定位与建图）中定位精度低、实时性差等问题，提出一种基于由初到精的位姿估计和双重闭环策略的SLAM方法。首先对MSER（最大稳定极值区）检测算法进行椭圆拟合化处理并提取出图像中的ROI（感兴趣区）;然后从ROI中提取出稀疏像素点并使用直接法得到初始位姿变换参数;接着结合改进的基于八叉树结构的ICP（迭代最近点）对相机位姿进行精估计;再结合关键帧选择机制提出一种双重闭环检测方法为构建的位姿图添加约束;最后通过g2o图优化框架对位姿图进行优化并完成点云的拼接。通过NYU和TUM标准数据集验证了算法的实时性与有效性，室内实验结果表明，在复杂环境下也能利用该方法进行准确的位姿估计，并构建出环境的三维点云地图。

关键词： SLAM; 移动机器人; 三维视觉; 位姿估计; 闭环检测; 点云拼接

中图分类号： TN95?34; TP242                    文献标识码： A                      文章编号： 1004?373X（2020）06?0034?05

A method of mobile robot localization and mapping based on 3D vision

CHEN Chao， ZHANG Weiwei， XU Jun

（School of Mechanical Engineering， Jiangsu University of Science and Technology， Zhenjiang 212000， China）

Abstract： A SLAM method based on the initial to precise pose estimation and double closed?loop strategy is proposed to improve the positioning accuracy and real?time performance in the 3D vision SLAM （synchronous localization and mapping） of mobile robot. The ellipse fitting processing is performed for the MSER （maximally stable extremal region） detection algorithm and the ROI （region of interest） in the image is extracted， and then the sparse pixels are extracted from ROI and the initial pose transformation parameters are obtained by means of the direct method. The camera pose is accurately estimated in combination with the improved ICP （iterative nearest point） based on octree structure. A double closed?loop detection method is proposed in combination with the key frame selection mechanism to add constraints to the constructed pose map. By means of the g2o map optimization framework， the pose map is optimized and the splicing of point cloud is completed. The real?time performance and effectiveness of the algorithm is verified with the NYU and TUM standard data sets. The results of indoor experiments show that in a complex environment， this method can also be used to accurately estimate the pose and construct a 3D point cloud map of the environment.

Keywords： SLAM; mobile robot; 3D vision; pose estimation; closed?loop detection; point cloud splicing

0  引  言

SLAM（同步定位与建图）主要指机器人在未知環境中，通过携带的传感器获取外界信息以完成对自身位姿的估计，并构建出周围环境的地图[1]。其中，以相机进行信息采集的方法称为视觉SLAM[2]，该方法可实现在复杂环境下的三维地图构建。

视觉SLAM大体分为两种，即特征点法与直接法。Artal 等人开源的ORB?SLAM2算法采用多线程处理[3]，虽能构建相对稠密的地图，但算法的运行效率较低。相较之下，直接法通过对像素进行操作，能较好地应对特征点缺失的情况。文献[4]提出一种稀疏直接SLAM算法DSO，该算法通过优化相机内参、位姿和地图几何参数，可完成定位并构建半稠密的地图，但算法运行于单目相机且实时性较差。2010年诞生的Kinect，是微软公司推出的一款能同时采集彩色图像和深度数据的相机[5]，利用它机器人能获取更加详细的三维信息，以进行更加精确的定位和三维地图构建。文献[6]通过校准、融合不同位置的Kinect传感器的信息来进行三维地图构建，但由于数据的获取与处理量过于庞大，使得系统的运行效率下降。KinectFusion通过点云配准进行位姿估计与三维地图构建[7]，但对硬件要求较高，需要通过配置GPU来实现，因此无法在一般平台上实时运行。

针对上述问题，本文提出结合特征法与直接法对相机位姿进行初估计，并将初始参数代入改进的ICP进行进一步的精确估计，以此获得最终的位姿轨迹。针对建图过程中的累计误差，结合关键帧策略提出一种双重闭环检测方法为构建的位姿图添加约束，并对位姿图进行优化，完成点云的拼接，从而得到全局一致的轨迹和地图。最后，通过实验对本文算法进行了验证和分析。

1  位姿初估计

1.1  椭圆化MSER检测

本文使用MSER算子[8]只对灰度图中的ROI（感兴趣区）进行提取。该算子是一种典型的ROI算子，描述的是图像中与相邻区域具有较高区分度的区域且具备良好的仿射不变性与抗噪性。由于MSER提取的区域具有不规则性，因此本文进行了椭圆拟合处理，公式为：

在灰度图中，不规则区域内点的坐标[（x，y）]用向量[X]表示，[R]表示MSER，[R]表示MSER中像素集合的势。式（2）为式（1）降维后得到的协方差矩阵。

式中，[D（x）]，[D（y）]，[COV（x，y）]分别为MSER中点集的横、纵坐标方差及两者的协方差，式（2）所需各分量的均值由式（3）给出。

通过计算可得该协方差矩阵的特征向量和特征根，由此可确定拟合椭圆的长短轴方向和幅值，图1中 [a1]和 [a2]分别为长轴和短轴的幅值，[α]代表长轴与 [x]的夹角。

1.2  稀疏直接法位姿估计

由于MSER区域中像素灰度相对变化较小，因此本文提出选取椭圆化MSER区域中心点[（E（x），E（y））]处的像素，通过直接法跟踪像素实现对帧间位姿的初步估计。直接法基于灰度不变假设，通过最小化两像素的光度误差来进行位姿优化：

式中，[e]为标量误差，误差的二范数[minξJ（ξ）=e2]作为优化的目标函数。对于[N]个空间点集[Pi]，优化函数变为：

此处需要知道[e]随相机位姿[ξ]如何变化，通过使用李代数的扰动模型，得到误差函数的雅克比矩阵：

接着利用高斯牛顿法计算增量，进行迭代求解，得到相机位姿变换矩阵记为[Tini]，并作为之后点云迭代配准的初值。

2  相机标定与点云生成

采用文献[9]中的标定方法对 Kinect进行标定，以此获得相机的内参数矩阵，完成校准后，图像中任意点的三维坐标可根据对应的深度信息得到，本文将提取出的MSER区域中所有像素点对应到深度图，以此得到三维点云数据。对于深度图中的任意像素点[（xd，yd）]，其三维坐标计算如下：

式中：[cxd]和[cyd]为图像的光心坐标;[fxd]和[fyd]为相机的焦距，由标定可得。

3  位姿精估计

对于点云模型P和Q，经典ICP算法通过构建点对间的误差函数并使用迭代方式计算两模型的变换关系，但存在迭代耗时、配准误差大等问题。本文结合八叉树结构对传统ICP进行了改进，具体步骤如下：

1） 建立基于八叉树模型的点云索引结构。其基本思想是：构建包围点云数据的最小外接包围盒，沿3个坐标轴方向对包围盒进行八等分。直到叶节点（子立方体）满足规定的阈值;否则，需要对叶节点继续八等分。剖分示意图如图2所示。

通过唯一对应任意一节点与一八进制数完成对叶节点的编码管理，即：

式中：[n]为节点深度;[qi]为八进制数， [q∈[0，7]，][i∈（0，1，2，…，i-1）]，[qi]表示该节点在兄弟节点中的编码。这样，从跟节点到叶节点的路径即可由[q0]到[qi]得到。

2） 点的K邻近快速搜索。点的K邻近是指在点云中离该点最近的K个点，只要确定了根节点，根据点云中任意一点的坐标即可计算出其八叉树编码。点云中点所在立方体的编码为：

根据周围小立方体的空间坐标，由式（9）可计算出对应的位置编码，由位置编码就可得到小立方体中对应的点的集合。对于点云中的任意一点，搜索其所在叶节点中距离其最近的点集，并搜索周围小立方体中的邻近点集，通过这一方式对八叉树中全部叶节点进行遍历，最终得到点云中所有点的K邻近。

3） 初始对准两点云模型。由于构建的模型过于理想化，因此需要一个迭代初值以避免算法陷入局部极值的情况，本文以直接法位姿粗估计得到的变换矩阵作为点到面ICP精配准的初值。目标误差函数为：

式中：[TTk-1=Tk];[Skj]是[qki]处的切平面，[qkj=（Tk-1li）?Q]是直线[Tk-1li]与[Q]的交点，[li]是[P]中点[pi]处的向量;[pi]是点云[P]中的点;[d]表示点到平面的距离。对于[P]中的各点[pi]，求出其法向量[ni]，并令[T0=Tini]。

4） 通過四元数法可得到使目标函数最小的变换参数[T]。

5） 将[T]作用于待配准点云P，Q，求取转换误差，并判断是否满足阈值要求，若满足，则迭代终止;否则，转步骤2），继续迭代。

6） 将满足要求的变换参数[T]用于最终的点云配准。

改进的 ICP 算法流程如图3所示，利用优化后的变换参数[T]即可对相机位姿进行精确估计。

4  闭环与优化

4.1  闭环检测

为了保证闭环检测与图优化结构的稀疏性，必须要定义关键帧。本文采取如下方法进行关键帧判别：

1） 将相机采集的第一帧作为关键帧，设置一定的时间间隔限制。若当前帧获取时间为[tc]，前一关键帧的获取时间为[tp]，则要满足[tc-tp≥εt]，令[εt=0.5 s]。

2） 用稀疏直接法估计当前帧和前一关键帧间相机运动，当运动量[D]大于阈值时，将该帧加入关键帧序列：

式中：[w1]为平移权重;[Δt]为帧间平移量;[w2]为旋转权重;[α，β，λ]为帧间旋转量。实验中发现相机运动估计对旋转比平移更为敏感，即当产生少量旋转或者大量平移时，将新帧加入关键帧序列，令[w1=（0.6，0.7，0.7）]，[w2=1]。         为降低闭环检测的计算量与判别误差，本文提出一种双重闭环检测方法，具体步骤如下：

1） 空间最近邻ICP匹配。

在以当前关键帧位置为中心，半径为R=0.3 m的球内检测闭环，即将当前帧与球内的其他帧进行ICP匹配。

式中：[Ikfk]为第[k]个关键帧;[Ii]为在第[k]和第[k+1]个关键帧间的数据序列;[ICP（I1，I2）]为位姿估计评价函数，若[I1]与[I2]配准成功，则[ICP（I1，I2）>0]，否则[ICP（I1，I2）≤0]。若匹配成功，则在两关键帧间建立一条边作为约束。

2） 稀疏直接法隨机检测。

从已有关键帧中随机抽取[n]帧，通过稀疏直接法估计它们与当前关键帧的变换矩阵，当帧间光度误差小于阈值[eθ=0.6]时，则把该帧选取为候选闭环，然后将光度误差最小的关键帧作为最终闭环，同时添加新的边作为约束。

4.2  图优化

本文采用g2o优化库[10]，对最终建立的位姿图进行优化。当优化了整个相机运动的位姿图后，将关键帧深度图对应的三维点云图进行拼接，从而得到全局一致的轨迹与地图。

5  实验结果与分析

为验证本文算法的有效性，分别在NYU和TUM标准数据集以及实际室内环境下进行了实验。其中，室内环境实验以TurtleBot2移动机器人为实验平台，搭载ROS操作系统[11]，采用Kinect深度相机获取数据，并使用笔记本电脑进行数据处理，如图4所示。

5.1  标准数据集实验

5.1.1  ICP算法验证

在NYUv2数据集上截取4段，分别为NYU_1，NYU_2，NYU_3，NYU_4，与经典ICP算法进行对比实验，结果如表1所示。

由表1知，经典ICP平均配准时间为1.099 s，平均配准误差为0.07 m;而改进的ICP平均配准时间为0.745 s，平均配准误差为0.06 m。经典算法耗时的主要原因是匹配点的搜索和迭代过程较慢;本文算法通过构建八叉树索引结构加快了点的搜索，同时，迭代初值的引入降低了配准的误差。

5.1.2  SLAM算法验证

为分析本文算法的运行效果，选取了TUM/fr1的4个数据集，通过与KinectFusion[7]以及ORB?SLAM2[3]两种算法在运行时间和轨迹RMSE（均方根误差）的实验，得到表2所示数据。

由表2计算得，本文算法的平均运行速度约为ORB?SLAM2的3倍，KinectFusion的1倍;轨迹误差约为ORB?SLAM2的39%，略大于KinectFusion，可知该算法在快速运行时也能保证较小的轨迹误差。

图5为三种算法在fr1/xyz场景下的建图结果，图6为该场景下的相机运动轨迹。可以看出本文算法能准确构建出环境的三维地图，同时对相机运动过程中的大部分轨迹做出了较准确的估计，只有小部分相机运动过快的地方出现了误差较大的情况。

5.2  室内环境实验

5.2.1  点云配准

图7所示为在实际场景下本文ICP与经典ICP的配准结果。可以看出，本文算法在最终配准精度上相较于传统算法有明显提高。图8为配准过程的误差收敛速度曲线，由于本文算法采用基于树的索引结构，因此误差收敛的更快;同时，引入迭代初值也使得最终的迭代次数更少，配准效率大大提高。

5.2.2  定位与建图

运用本文算法可在机器人移动过程中生成三维地图以及运动轨迹。实验室长约7 m，宽约5 m，使用罗技游戏手柄控制机器人以0.2 m/s的速度绕室内移动一周左右以形成闭环，如图9所示。

从图中可以看出，在机器人运动的同时增加了当前位姿和之前位姿间的联系即增加随机闭环和近距离闭环，此方法可有效消除系统累计误差，进一步提高定位精度。图10为本文算法和另外两种算法在机器人运动60 s时的轨迹误差对比，由于本文采用了由粗到精的位姿估计以及混合闭环检测方法，相较于ORB?SLAM2在轨迹精度上提高了约40%，与KinectFusion较为接近。图11为机器人运动过程中构建的实时三维点云地图，可以看出环境的整体结构以及局部小场景均得到较好的描述。

6  结  论

本文提出一种基于由初到精的位姿估计和双重闭环策略的SLAM方法，可有效解决移动机器人三维视觉SLAM中定位精度低、实时性差等问题。实验结果表明，改进的基于迭代初值和八叉树结构的ICP方法能有效降低点云配准误差，提高配准效率，从而使得机器人的定位精度与运行效率大大提高。此外，结合提出的闭环检测策略，本文算法可实时有效地构建出环境的点云地图。受限于Kinect相机的采集距离以及动态物体的存在，本文算法对室外大场景还不大适用，今后将通过多传感器融合和算法优化来实现对室外场景的地图构建。

参考文献

[1] SHAMSUDIN A U， OHNO K， HAMADA R， et al. Consistent map building in petrochemical complexes for firefighter robots using SLAM based on GPS and LIDAR [J]. ROBOMECH journal， 2018， 5（1）： 7.

[2] EADE E， MUNICH M E， FONG P. Systems and methods for VSLAM optimization： US20120121161 A1 [P]. 2012?03?06.

[3] MUR?ARTAL R， TARD?S J D. ORB?SLAM2： an open?source SLAM system for monocular， stereo， and RGB?D cameras [J]. IEEE transactions on robotics， 2017， 33（5）： 1255?1262.

[4] ENGEL J， KOLTUN V， CREMERS D. Direct sparse odometry [J]. IEEE transactions on pattern analysis and machine intelligence， 2018， 40（3）： 611?625.

[5] PENG Yanfei， PENG Jianjun， LI Jiping， et al. Design and development of the fall detection system based on point cloud [J]. Procedia computer science， 2019， 147： 271?275.

[6] MENG X R， GAO W， HU Z Y. Dense RGB?D SLAM with multiple cameras [J]. Sensors， 2018， 18（7）： 2118?2130.

[7] TENG C H， CHUO K Y， HSIEH C Y. Reconstructing three?dimensional models of objects using a Kinect sensor [J]. Visual computer， 2018， 34（11）： 1507?1523.

[8] FAN Yihua， DENG Dexiang， YAN Jia. Natural scene text detection based on maximally stable extremal region in color space [J]. Journal of computer applications， 2018， 38（1）： 264?269.

[9] LACHAT E， MACHER H， MITTET M A， et al. First experiences with Kinect V2 sensor for close range 3D modelling [J]. International archives of photogrammetry， remote sensing and spatial information sciences， 2015， 40（5）： 93?100.

[10] JIA Songmin， LI Boyang， ZHANG Guoliang， et al. Improved KinectFusion based on graph?based optimization and large loop model [C]// 2016 IEEE International Conference on Information and Automation. Ningbo： IEEE， 2016： 813?818.

[11] KOUB?A A. Robot operating system [J]. Studies in computational intelligence， 2016， 1（6）： 342?348.