基于拉普拉斯金字塔和CNN的医学图像融合算法
吴 帆,高 媛,秦品乐,王丽芳
中北大学 大数据学院,太原 030051
1 引言
随着计算机技术的快速发展,医学成像技术已经成为各种临床应用中的重要组成部分,获取医学影像有X射线、计算机断层扫描(Computed Tomography,CT)、磁共振(Magnetic Resonance,MR)、正电子发射断层扫描(Positron-emission Tomography,PET)等多种方式。由于成像机制的不同,具有不同模态的医学图像呈现不同类别的器官/组织信息,医生根据实际情况选择不同成像方式。多模态医学图像融合的目的在于,将包含不同补充信息的不同模态的源图像组合生成可视化的合成图像,帮助医生更好地做出诊断和决策[1]。
早期以取平均、HIS变换、高通滤波器、主分量分析等为图像融合的主流方法,只在一个层上对图像进行分解处理和融合操作[2]。到20世纪80年代中期,由于金字塔分解具有多方向提取图像特征的特性,基于金字塔分解的图像融合方法开始发展并应用[3]。20世纪90年代开始,小波变换以多分辨率的特点为图像融合提供了新的工具,使图像融合技术得到进一步发展[4]。近年来,多模态医学图像融合的研究主要集中于基于多尺度变换理论的图像融合方法[5],如基于形态金字塔的方法、基于离散小波变换的方法、基于双树复小波变换的方法和基于非子采样轮廓线变换的方法。基于多尺度变换的方法一般为分解、融合和重构的三步框架[6],基本原理是在选定的变换域中通过分解系数来测量源图像的活动水平。其次,还有基于独立分量分析和稀疏表示等的融合方法,其通常采用滑块进行近似探索,寻找计算活动水平的有效特征域,将图像转换成单一尺度的特征域。但这些方法都需要依赖先验知识选取活动水平,实验结果在很大程度上受到人为因素的影响。
此外权重图构造的研究也是影响融合效果的关键。在传统的融合方法中,权重图一般通过活动水平测量和权重分配两个步骤来实现,为了提高融合性能,在文献[7-10]中提出了许多复杂的分解方法和精细的权重分配策略,但其依然是依据先验知识对两个步骤进行优化组合,大大限制了算法的性能。而深度学习通过网络学习参数,能将活动水平测量和权重分配以最好的方式在图像融合中,并因其强大的特征提取能力已成功应用于车牌识别、面部识别、行为识别、图像分类和语音识别等领域[11]。Liu等人训练深度卷积神经网络(Convolutional Neural Network,CNN)联合生成活动水平测量和融合规则,应用于红外和可见光图像[12],证明了基于CNN的算法可以提供比传统的基于空间域变换的算法具有更好的性能。Zhong等人在多模态图像融合中提出了一种基于CNN的联合图像融合和超分辨率方法[13];Liu等人介绍了用于图像融合的卷积稀疏表示[14],反卷积网络构建层的层次结构,每个层由编码器和解码器组成;在遥感图像融合中,Giuseppe等人提出了一种有效的三层结构来解决泛锐化问题[15],通过添加非线性指数来增强输入,以促进融合性能。但CNN直接应用于医学图像融合中,存在伪影影响实验结果,不符合人类视觉感知效果,且利用经验对滤波器参数进行初始化,很难保证训练的网络具有良好的训练效果。
本文提出了一种基于金字塔和卷积神经网络的医学图像融合方法。通过更有利于人类视觉感知的金字塔的多尺度分解[16]来提高融合效果,同时引用支持向量机的思想对CNN网络进行改进,使其不依赖于经验初始化参数,有效地提取图像特征,得到更适合的权重图,并去掉传统CNN网络中的池化层/采样层以减少图像信息的损失。
2 相关工作
2.1 拉普拉斯金字塔
拉普拉斯金字塔(Laplacian Pyramid,LP)是一种多尺度、多分辨率的图像处理方法,可以将图像的边缘和纹理等特征按照不同的尺度分解到不同分辨率的塔层上,再将多幅源图像的对应塔层分别进行融合,得到融合后的金字塔以后,再重构得到最终融合图像。LP在多尺度上融合不同模态的医学图像领域已有广泛应用,但其存在伪影的问题,Paris等人提出了具有简单、灵活特点的区域拉普拉斯金字塔(Local Laplacian Pyramid,LLP)来克服这一问题。
LLP是基于LP的边缘感知滤波器,滤波器的输出O为重构图像,Si为每层图像,v为原始图像拉普拉斯金字塔分解得到的系数,I′(v)为由其得到的新系数,collapse()为重构算子。

对于每个系数I(v)=(x,y,i),通过点映射函数生成一个新的系数I′(v):
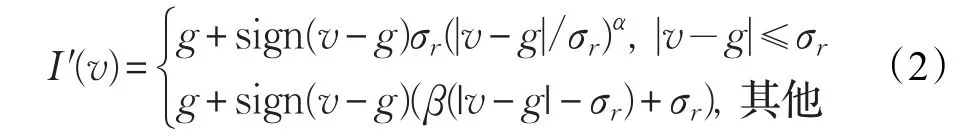
其中,x,y分别代表水平和垂直方向的像素坐标;i代表金字塔的水平参数,v是位置(x,y)的像素值;g是从高斯金字塔得到的图像值;LLP有三个自由参数:(1)强度阈值σr作为区分边缘信息和细节信息的边界;(2)细节因子α控制细节增强量(0≤α≤1);(3)测距因子β控制范围的缩小(0≤β≤1)或扩大(β>1)。
2.2 卷积神经网路
CNN是一个典型的深度学习模型,与普遍神经网络相同具有多层感知结构学习具有不同抽象层次的信号/图像数据的各层特征表示[17],是一种可训练的前馈网络,每层包含一定数量的特征映射。特征图中的每个单元称为神经元。通过对神经元进行线性卷积、非线性函数激活应用于神经和空间池化等操作连接不同层的特征图[18]。
局部感知、权值共享和池化是CNN的三大核心思想[19],使CNN可以在一定程度上获得平移不变性和缩放不变性。在多层感知机中,一般情况下隐藏节点与图像的各个像素点进行全连接,但其在卷积神经网络中,仅将隐藏节点与图像中足够小的局部像素点进行连接,该操作很大程度上减少了需要训练的参数。不同的图像或者相同图像的不同位置之间进行权值共享,可以减少卷积核的数量,避免卷积核的重复,从而进一步减少参数。源图像在经过卷积操作之后通过下采样操作缩小图像尺寸的过程叫做池化,该操作可以减少过拟合发生的概率,降低了特征图的维度,达到减少计算量,提升计算速率的目的。
2.3 支持向量机
在机器学习领域,支持向量机(Support Vector Machine,SVM)是一个有监督的学习模型,通常用来进行模式识别、分类,以及回归分析。支持向量机旨在通过有限样本信息寻求模型的复杂性和学习能力之间的最优解,获得最好的应用能力[20]。凸优化问题可以很好地表示SVM学习问题,采用现有的有效算法发现目标函数的全局最小值。
SVM模型中所有分类点在各自类别的支持向量两边,即所有点到超平面的距离大于一定的距离。用数学式子表示为:

其中,yi(WTxi+b)=γ'(i)≥γ'(i=1,2,…,N)。一般都取函数间隔γ'为1,这样优化函数定义为:

3 改进的医学图像融合策略
3.1 融合过程
本文提出的医学图像融合算法原理图如图1所示。该算法可以概括为以下四个步骤:
(1)基于改进的CNN权重图的生成
将源图像A和B分别输入到改进的CNN卷积网络中,如2.2节所示,生成权重图W。

图1 医学图像融合过程
(2)金字塔分解
采用金字塔的多尺度分解图像的方法,使融合在每个分解水平进行,将每个源图像通过区域拉普拉斯金字塔进行分解。L{A}l和L{B}l分别表示A金字塔和B金字塔的第l层分解,同样将权重图W输入区域拉普拉斯金字塔得到第l层分解L{W }l。取为最高分解层数,其中H×W为源图像大小,表示floor函数。
(3)系数融合
对于每一个l的分解层,计算L{A}l和L{B}l的区域能量图[17]。
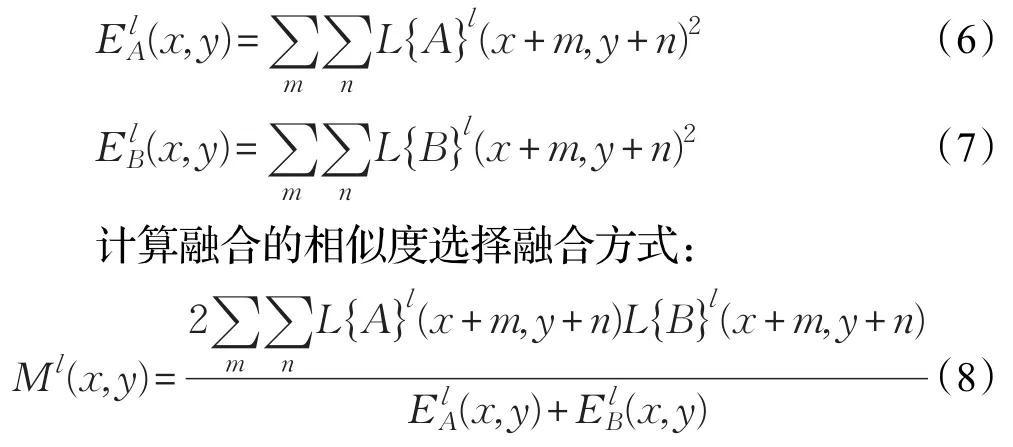
其值范围为[1,−1],接近1表示相似性高。设置一个阈值t,如果Ml(x,y)≥t,采用公式(9)的融合规则:
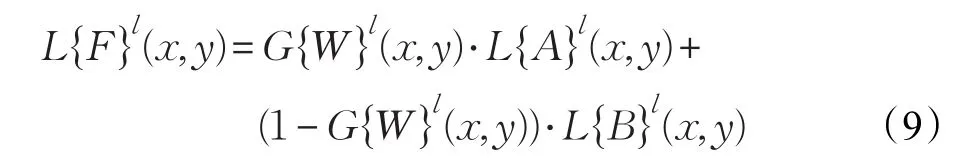
如果Ml(x,y) (4)拉普拉斯金字塔重建 对L{F}l进行区域拉普拉斯金字塔重构得到融合图像F。 对卷积神经网络(CNN)进行改进,首先,采用经验风险最小作为神经网络的评价指标很难保证训练出的网络具有良好的泛化性,将基于经验风险最小化的评价指标替换为基于结构风险最小化。其次,传统CNN的残差通过梯度下降法[21]向后传播,交替使用多个卷积和最大池化层,对提取的特征进行分类,得到基于输入的概率分布,改进的CNN模型中降维是通过步长为2的标准卷积层来实现。 Rd为输入,y为输出,d为维度,令x∈Rd(y∈R),W 为权值,b为偏置,ϕ(x):为对x通过卷积操作C后,通过隐层神经元转为函数映射,q为变换后的维度[22]。当目标函数可以定义为: 基于深度神经网络学习的思想,假设输出等于输入,与SVM中权值求解的思想类似,估计函数为: 利用迭代算法对网络参数进行优化,首先,对于一个固定的C,求解为: 若Q=A(I-1BT)为N×N的矩阵,如果通过对应的输入向量在映射邻域中心中的支持值来估计像素点(x,y)的支持值,用矩阵Q的中心行向量得到的支持值滤波器对图像进行卷积,可获得全部图像的支持值C。 CNN中最大池操作的公式: ψ表示每个卷积层获得的输入图像的特征图,是大小为W×H×G的三维阵列,其中H和W为高、宽,G为通道数,最大池化层的大小为k(k=2)和步长为r。当g(h,w,i,j,u)=(r⋅i+h,r⋅j+w,u)是S在一定步长下到ψ的函数映射。当r>k时,最大池层不重叠;通常CNN模型取k=3和r=2最大池化层存在重叠。类似最大池化操作的公式得出标准卷积层的公式: θ是核权值,i,j和u代表在尺度u上的像素的坐标(i,j)。一般使用ReLU作为激活函数用(f•)表示,f(x)=max(x,0),o∈[1,M]是卷积层输出特征的数量,该操作依赖于与前一层特征图中反馈的元素。对比公式(17)、(18)可知,当θh,w,u,o=1且u=o=0 时,(f•)等价于p范式。在传统CNN模型中最大池的主要作用于特征图的维度和在一定程度上保持特征尺度不变性。基于以上公式得出的结论,具有相对应的核和步长的标准卷积层可以学习最大池化操作并将其替换[23-25]。 改进的CNN模型不依赖于学习过程中的经验风险,可以自适应地学习各个分解层次的最优滤波器,有效地从图像的各个层次提取细节,同时标准卷积层的应用避免了采用池化层导致的信息丢失问题。改进的CNN模型结构如图2所示。 图2 改进的CNN模型结构 (1)根据公式(13)~(16),得到矩阵 Q 的中心行向量;构造核权值,得到滤波器。 (2)将两个源图像输入改进的CNN模型,输入图像经过卷积操作和滤波器得到输出图像。 (3)改进的CNN模型在第一层通过3×3的滤波器输出特征图维数为64,第二层卷积层通过3×3的滤波器输出特征图维数为128,这两个卷积层的步长设为1;设置第三层卷积的滤波器大小为3×3,步长为2,得到特征图维数为256;第四层将维数为256的特征图输入,通过3×3的滤波器得到得到特征图维数为256。 (4)将特征图输入到全连接层,输出最终结果。 本文实验使用的是美国哈佛医学院(Harvard Medical School)的数据集(http://www.med.harvard.edu/AANLIB/home.html),全脑图谱由Keith A.Johnson和J.Alex Becker创建,提供正常脑和一些常见疾病的脑部图像。实验环境由硬件环境和软件环境构成,硬件环境为测试实验所用的Intel Xeon服务器,搭载2块NVIDIA Tesla M40的GPU,每块显存12 GB,共24 GB;软件环境为64位Ubnutu 14.04.05 LTS操作系统,Tensorflow V1.2,CUDA Toolkit 8.0,Python 3.5。 选取脑膜瘤、脑梗、脑中风三种类型的CT和MR图像对本文算法进行融合仿真实验。如图3所示。 将本章算法与NSCT-PCNN算法[26]、文献[27]算法、文献[28]算法、文献[29]算法与本文算法相比较。NSCTPCNN算法利用NSST对源图像进行多尺度、多方向分解,低频子带系数采用基于区域特征加权的方式进行融合;高频内层子带系数采用PCNN求出区域点火特性,与平均梯度加权进行选择,高频外层子带系数采用区域绝对值取得[26]。文献[27]算法是把提升小波变换和PCNN相结合进行图像融合,该算法高频部分使用自适应PCNN方法,低频使用区域能量算法。文献[28]算法是基于曲面小波变换算法,首先,使用surfacelet转换分解源图像;然后,有效地结合低频和高频系数;最后,逆变换生成融合图像。文献[29]中高频部分采用CS来减少计算复杂度,低频采用自适应PCNN方法,并选取了SDS特征作为外部激励,对应神经元处的连接强度采用SDG特征。 第一组脑膜瘤实验中,NSCT-PCNN算法没有很好地保存MR源图像中的细节信息,存在一些伪影,文献[27]算法亮度太高造成了信息丢失,文献[28]算法视觉效果相对好一些,但是存在同样的问题。对比而言,文献[29]算法和本文算法的融合结果相对较好,有较好的清晰度,但本文算法针对MR源图像中软组织的信息保存度上更为突出,融合效果最好。 第二组脑梗实验中,NSCT-PCNN算法处理的图像整体较暗,并且细节信息表现不明显,视觉效果明显不好,软组织信息难以确定,文献[27]算法中融合效果不错,但图像中间部分的细节表现力不强,文献[28]算法中对比度较差,同时丢失了骨骼信息,文献[29]算法的视觉效果相对稳定,骨骼清晰,但与本文算法对比,对比度不够,图像中信息丰富程度略有逊色。 第三组脑中风实验中,从视觉效果上看,NSCTPCNN算法中图像纹理细节信息不清晰,图像整体模糊,文献[27]算法得到的图像边缘出现伪影,信息丢失严重,文献[28]算法得到的图像具有较好的亮度,但是图像整体轮廓丢失严重,文献[29]算法的图像包含纹理信息丰富,符合人类的视觉感知,本文算法融合图像视觉效果较好,图像清晰。 图3 融合效果对比图 为了更加全面地评价融合结果,本文采用了互信息(Mutual Information,MI)、信息熵(Information Entropy,IE)、结构相似性(Strructural Similarity,SSIM)、空间频率(Space Frequency,SF)和平均梯度(Average Grads,AG)五项指标进行评价,指标的值与融合效果呈正相关。 由表1中客观指标可得,MI用于表示信息之间的关系,是图像随机变量统计相关性的测量,值越大代表图像的相关性越高,在脑膜瘤、脑梗、脑中风三组实验中本文算法均达到最优,分别达到23%、4.3%、20.5%的提升。IE表示图像中包含的信息平均量,融合的目的在于使图像包含更多的信息,本文算法在脑膜瘤实验中,IE数值仅次于文献[28]算法,在脑梗和脑中风实验中均达到最优,且平均提升22.2%和13.6%。SSIM分别从亮度、对比度、结构三方面度量图像的相似性,值越大表示图像中结构信息越相似,在三组实验中本文算法对比NSCT-PCNN算法、文献[27]、文献[28]和文献[29]算法平均提升5.6%、18.4%、19.7%。SF反应图像灰度的变化率,图像中不同图像成分具有不同的空间频率,SF越高,图像的亮暗变化、短距离突变更明显,本文算法在三组实验中都仅次于文献[27]算法,但结合主观评价可知文献[27]算法边缘亮度均较强,导致了边缘细节信息不明显的问题,不符合人类视觉感知,同时相对于其他算法,本文算法也略有提升。AG反映图像微小细节变化的速率,其变化率的大小可以表征图像的清晰度,其在三组实验中数值均达到最优,反映了本文算法的融合图像在对纹理信息和细节信息的清晰保存上具有绝对的优势。总体而言,在客观指标上,说明了本文算法性能最优,不仅包含的信息量最多,较好地保留了融合图像的细节部分,而且对边缘信息的损失较少,客观评价与视觉观察结果相符,为精确的病灶定位及手术治疗提供有利的影像依据。 为验证本文算法的准确性,对改进CNN训练过程中函数损失的实验数据如图4所示。 表1 实验的客观指标 图4 本文算法损失 从图4可知,从曲线的整体来看,随着迭代次数的增加,迭代次数低于50 000次时呈急剧下降趋势,迭代次数高于50 000次之后逐渐趋于平缓并达到一个相对稳定的数值,通过综合权衡损失,确定本文实验的最终迭代次数为150 000次。 本文算法通过将金字塔与改进的卷积神经网络结合起来,为了达到人眼视觉感知的良好效果采用了多尺度处理和自适应选择融合方式的图像融合技术,克服融合结果存在伪影的问题;通过卷积神经网络提取图像特征,减轻了人工设计活动水平测量和权重分配对实验结果的影响。实验结果表明,该算法在主观评价和客观评价方面均获得高质量的结果,接下来将算法更好地应用于其他领域还需要更好的探索和验证。
3.2 改进的CNN模型



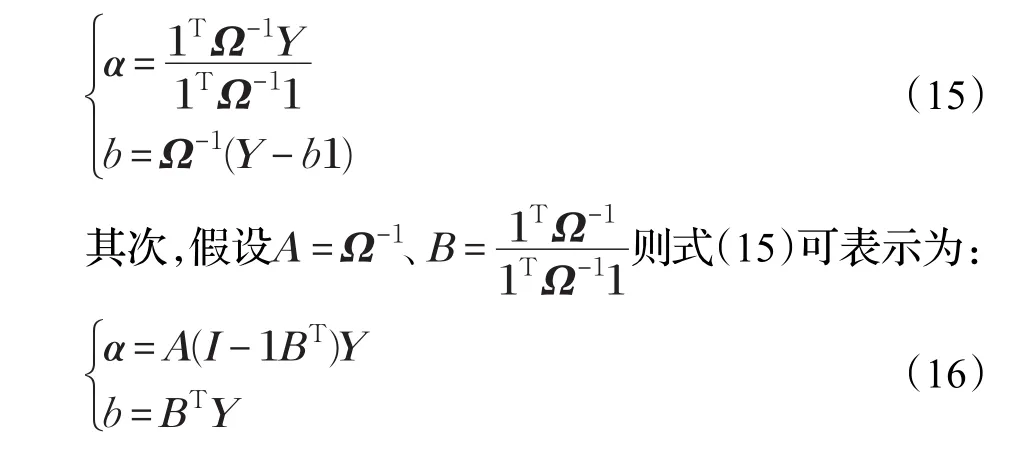



4 仿真实验与结果分析
4.1 融合效果

4.2 评价指标


5 结语

