基于贝叶斯网络的水下采油树系统剩余寿命预测*

袁晓兵 陈国明 范红艳 邵筱焱 杨 超 葛伟凤 蔡宝平

（1.中国石油大学（华东）机电工程学院 山东青岛 266580； 2.中海油安全技术服务有限公司 天津 300456）

近年来水下采油树系统故障引发的事故时有发生，不仅影响了油气的正常开采，而且大量油气的泄漏、平台的破坏等甚至会造成巨大的经济损失乃至人员伤亡。及时预测水下采油树系统的故障隐患及剩余寿命，是油气安全生产保障中亟待解决的问题。

一些国外的研究认为，水下采油树系统可靠性评估的局限性不在于技术的发展，而是相关的可靠性参数不易获得［1］。针对这一观点，Granhaug［2］提出了基于随机故障和可靠性参数的仿真模型，该模型可根据修复船的要求、调动、工作时间及潜在的天气情况等预测停工期；Li等［3］提出了一种具有较高精度和效率的、基于蒙特卡罗方法的随机规划模型数值求解策略，解决了岩质边坡由于包含多种破坏模式参数随机性和可变性高而导致的可靠性分析难度增加的问题。国内研究主要聚焦于水下采油树系统各组件的剩余寿命预测。吴忠等［4］通过对油气长输管道的腐蚀特点及腐蚀影响因素的分析，结合当前存在的腐蚀寿命预测技术，提出了腐蚀管线剩余寿命预测技术；陈卫东等［5］针对水下采油树系统的可靠性提出了故障树分析方法，得到了水下采油树系统管汇失效概率随时间的变化曲线，进而可以确定维修时间间隔，对实际工程的经济性、安全性等有着重要意义。

本文综合分析了水下采油树系统的结构和特性，将相互依赖性及剩余寿命预测2部分内容相结合，建立了水下采油树系统的贝叶斯网络模型。水下采油树系统各组件之间存在着错综复杂的关系，其中某一组件或模块的失效会因地理位置或结构功能的关系而影响到其他组件及模块的可靠性。相较于陆上设施所遇到的风险，海上设施风险率要高得多，而在众多海上设施中，FPSO的风险率又明显高于其他海上设施，因此本文从FPSO的突发失效入手，通过不同组件及模块间的相互依赖性关系，预测其对整体水下采油树系统的影响。

1 水下采油树系统各模块的相互依赖性

相互依赖性（interdependency）是设备间存在的一种双向影响的内在作用，对系统的可靠性有着较强的影响［6］。当基础设备的一部分由于外部冲击或内部退化等原因产生突发失效时，由于相互依赖性的存在，冲击会继续扩大继而对整个系统的安全构成威胁。由于每个组件的状态均将影响其他相关组件的状态，并且受其他相关组件状态的影响，因此，对不同组件间的交互作用建模将是最具挑战性的问题。此外，当前针对相互依赖性建模的难点还表现在建模对象的复杂性、忠实度与抽象度之间的权衡、后果的度量及信息的获取方面［7］。Albert和Holmgren等［8-9］通过使用简化或抽象的方法，利用较少的数据和运行时间实现了建模与仿真。

相互依赖性可分为地理位置相互依赖性、功能相互依赖性和后果相互依赖性。其中，地理位置相互依赖性是由于系统在地理位置上相邻并且可能导致共因故障；功能的相互依赖性与连锁故障相关；而后果相互依赖性与升级故障相关［7］。事实上，大多数系统在承受冲击或疲劳退化的过程中，可靠性和剩余寿命的减少是由地理位置和功能相互依赖性共同决定的。

水下采油树系统主要结构如图1所示。按照地理位置、结构功能及各组件的相关特性等，可将该系统分为水上部分、水下部分及浮式生产储油轮

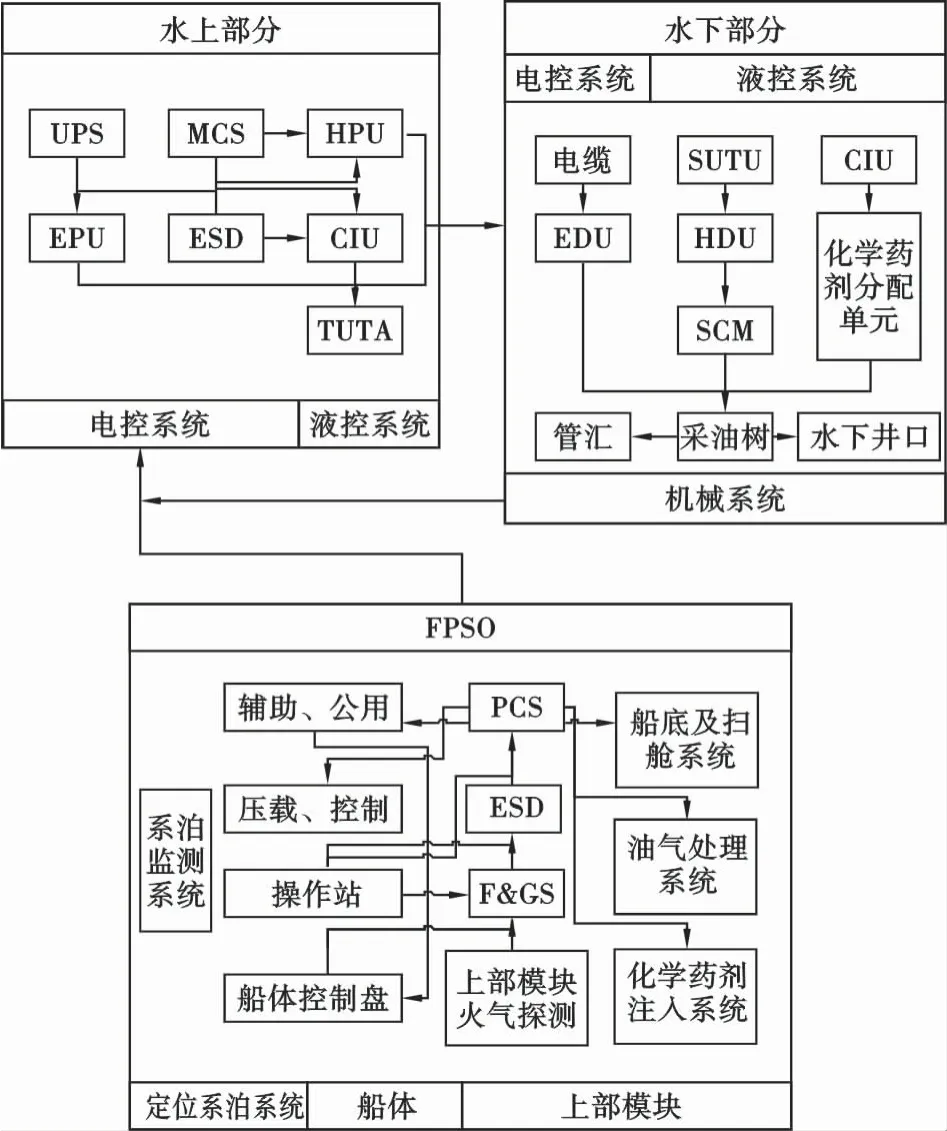
图1 水下采油树系统主要结构的模块划分Fig.1 Module division of the main structures of subsea Christmas tree system

（floating production storage and offloading，FPSO）3个模块。水上部分模块划分为电控系统、液控系统；水下部分模块划分为电控系统、液控系统和机械系统；FPSO划分为定位系泊系统、船体及上部模块。其中，水上部分与FPSO存在着地理位置上的相互依赖性，而与水下部分存在着结构功能上的相互依赖性，故水上部分的可靠性由水下部分和FPSO共同决定，而FPSO与水下部分又反作用于水上部分，例如当FPSO中的PCS由于冲击而受到破坏时，水上部分电控系统的可靠性会受到影响，进而影响水下部分电控系统的可靠性。由于FPSO结构的复杂性，为了使建模过程不至于太过繁琐，考虑到上部模块是FPSO的核心组成，本文将重点考虑上部模块中的PCS、ESD和F＆GS 3个组件之间及其与水上部分、水下部分间的相互依赖性。

2 无相互依赖性的剩余寿命预测

2.1 贝叶斯网络模型的建立

基于图1的水下采油树系统，在Netica软件中建立并运行相应的贝叶斯网络，如图2所示。图2是未扩展前的贝叶斯网络，通过时间扩展节点（t节点）完成动态扩展，能够得到随时间变化的可靠性。该贝叶斯网络由节点和有向连接线组成：节点表示影响可靠性变化的参量，由节点名称和节点概率分布表组成；节点名称后的数字表示时间；有向连接线表示参量间由父节点指向子节点的作用关系，其中黑色箭头表示在当前时间片内的参量间关系，而红色箭头代表动态贝叶斯网络中两相邻时间片的参量作用关系。

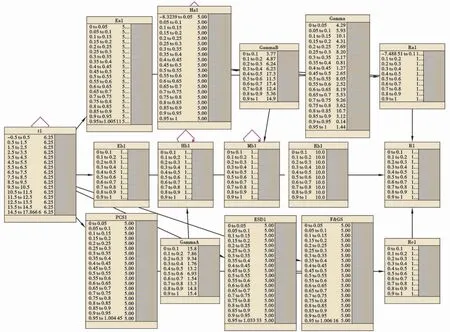
图2 无相互依赖性的水下采油树系统贝叶斯网络模型Fig.2 Bayesian network model of subsea Christmas tree without interdependence

电控部分的可靠性退化过程服从指数分布；液控和机械部分的可靠性退化过程服从伽马分布［10］；而PCS、ESD和F＆GS节点按其结构原理可被划分为电控部分，因此这3种节点的退化过程也服从指数分布。

指数分布和伽马分布的可靠性公式为

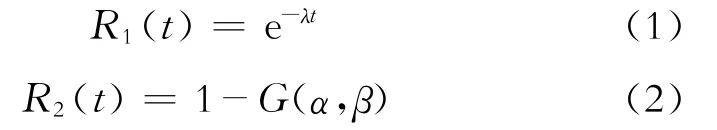
式（1）～（2）中：R1（t）和R2（t）分别为指数分布和伽马分布下的可靠性；λ为对应模块或组件的失效率，G为伽马函数，α为形状参数，β为尺度参数，可由均值、方差等计算获得；t为时间，a。

水下采油树系统各组件之间存在着串联或并联关系。串联关系表示缺一不可，一旦其中一个组件发生失效，那么系统就会失效；并联关系常用于冗余状态，即系统的所有组件均处于失效状态时系统才会失效，而部分或一个组件的失效不会引起系统的失效。系统与组件间可靠性的相关关系为［11］

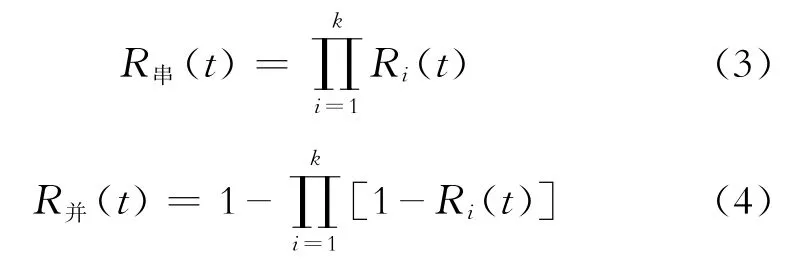
式（3）～（4）中：R串（t）为t时刻串联系统的可靠性；R并（t）为t时刻并联系统的可靠性；Ri（t）为t时刻第i个模块的可靠性；k表示模块总数。

由于水下采油树系统各组件有着各自独立的功能，为了简化建模过程，本文不考虑组件冗余的并联关系，而只考虑串联关系下系统考虑相互依赖性的可靠性，由式（3）可得出水下采油树系统的整体可靠性：

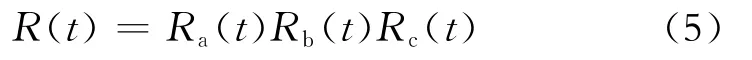
式（5）中：R（t）为水下采油树系统的整体可靠性；Ra（t）、Rb（t）和Rc（t）分别为水上部分、水下部分和FPSO在t时刻的可靠性。

2.2 贝叶斯网络模型参数的获取

由于难以获得贝叶斯网络模型中各节点大量、准确的参数值，因此参考汪航等［13］提出的方法，将海上设备可靠性数据库（OREDA）［12］与贝叶斯方法相结合模拟失效过程。其中，平均失效率和标准差的计算见式（6）和式（7）［13］，从OREDA数据库提取的相关数据及相关计算值见表1。

式（6）～（7）中：λd为平均失效率；Sd为标准差。

将表1中的参数输入贝叶斯网络模型，建立无突发失效情况下不考虑相互依赖性的水下采油树系统剩余寿命预测原始模型。为了得到水下采油树系统可靠性的连续变化曲线，本文将未扩展的贝叶斯网络模型扩展为动态贝叶斯网络模型，定义动态贝叶斯网络的一个时间片为1 a，将已建立好的模型扩展为15个时间片，即15 a。

表1 海上设备可靠性数据库中采油树系统节点参数的指数分布和伽马分布Table 1 Node parameters of exponential distribution and Gamma distribution of Christmas tree in OREDA database

2.3 无相互依赖性下的可靠性及剩余寿命

根据图2采油树系统无相互依赖性的贝叶斯网络模型，得到无相互依赖性下水下采油树系统各模块的可靠性变化趋势，如图3所示。水下采油树系统的水下部分由于面临海水静水压力高、温度低、采油树压力高、腐蚀严重等各种复杂的海洋环境，因此同一时刻内相较于水上部分及FPSO，有着较低的可靠性，且其退化速率更快；水上部分和FPSO由于其功能、地理位置等的相似性，可靠性的整体变化趋势是相似的；由于FPSO在采油过程中与穿梭油轮对接时易出现碰撞等情况，且单点系泊FPSO易发生单点断裂、倒塌和碰撞等事故，导致FPSO在同一年内的可靠性总体低于水上部分；整体可靠性曲线低于任一模块的可靠性，其退化过程先快后慢且呈指数分布，整体可靠性在第8～9 a降至0.1以下。

图3 无相互依赖性的水下采油树系统可靠性Fig.3 Reliability of the subsea Christmas tree system without interdependence

组件的可靠性越低，完成对应功能的能力就越小，造成系统失效的几率就越高。水下采油树系统剩余寿命预测的常用方法是设置失效阈值，并将其与相应的可靠性退化曲线结合，剩余寿命值实际上是检测时间和失效时间的间隔。结合实际情况及专家经验［14］，当组件的可靠性下降至0.1～0.2时，组件已不能完成基本功能，因此将无相互依赖性水下采油树系统的失效阈值设置为0.1，计算正常情况下（无相互依赖性）的水下采油树系统剩余寿命，如图4所示。可以看出在无相互依赖性条件下，水下采油树的水下部分剩余寿命为10.75 a，在扩展的有限时间片内，水上部分和FPSO的可靠性远远没有降至失效阈值0.1，水上部分和FPSO的剩余寿命均超过12 a，水下采油树系统的整体剩余寿命为8.2 a。在不考虑退化日常维修的情况下，水下采油树系统组件的剩余寿命将集中在10～12 a，该预测结果与实际情况也较为符合。

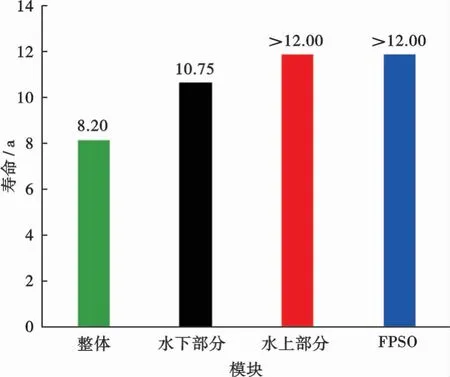
图4 无相互依赖性的水下采油树系统剩余寿命Fig.4 Remaining useful life of subsea Christmas tree system without interdependence

3 考虑相互依赖性的剩余寿命预测

3.1 FPSO突发失效的贝叶斯网络模型

根据OREDA数据库可知，水下采油树系统设备往往面临着多种失效模式，包括致命失效、渐衰失效、早期故障和未知故障等，而这些故障又可被细分为仪表读数异常、外部泄漏、传热不足、内部泄漏、运行故障、过热、参数偏差和结构缺陷等［12］。为了简化突发失效下的贝叶斯网络，建立退化模型时假定只有FPSO的PCS组件出现故障，对FPSO、水上部分、水下部分及整个水下采油树系统的可靠性做出预测。

PCS的主要突发失效模式包括临界和退化2种模式［11］，突发失效率分别为2.81×10-6次／h和6.18×10-6次／h，由于临界模式的失效率小于退化模式，因此临界模式的失效强度小于退化模式。假定PCS在第4 a因受到冲击而突发失效，则从该时刻起，PCS的可靠性将随其失效率的变化而发生改变。

如果不考虑与水上部分、水下部分的相互依赖性关系，则PCS的可靠性变化只会引起FPSO可靠性的变化，其贝叶斯网络模型如图5所示，临界突发失效和退化突发失效2种模式的结构模型相同，仅改变模型中节点的参数便可计算相应的可靠性。

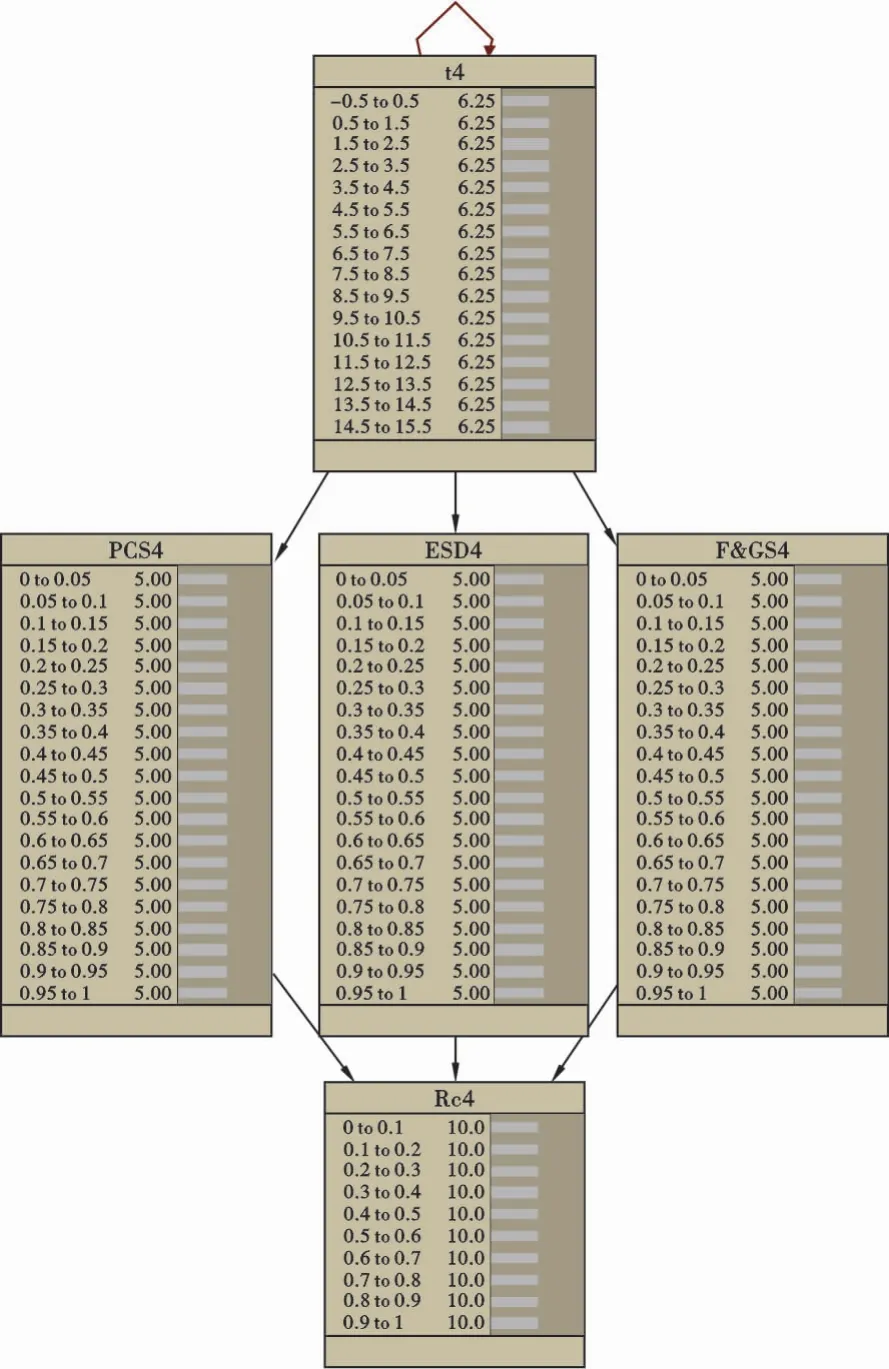
图5 FPSO突发失效的贝叶斯网络模型Fig.5 Bayesian network model of FPSO under sudden failures

根据FPSO突发失效的贝叶斯网络模型得到的可靠性变化如图6所示。可以看出，在FPSO发生突发失效的第4 a后，3种失效模式的可靠性均随时间的延长而降低，且退化趋势基本一致，退化突发失效的可靠性比临界突发失效降低得更多。因此，退化突发失效对FPSO的影响更大。

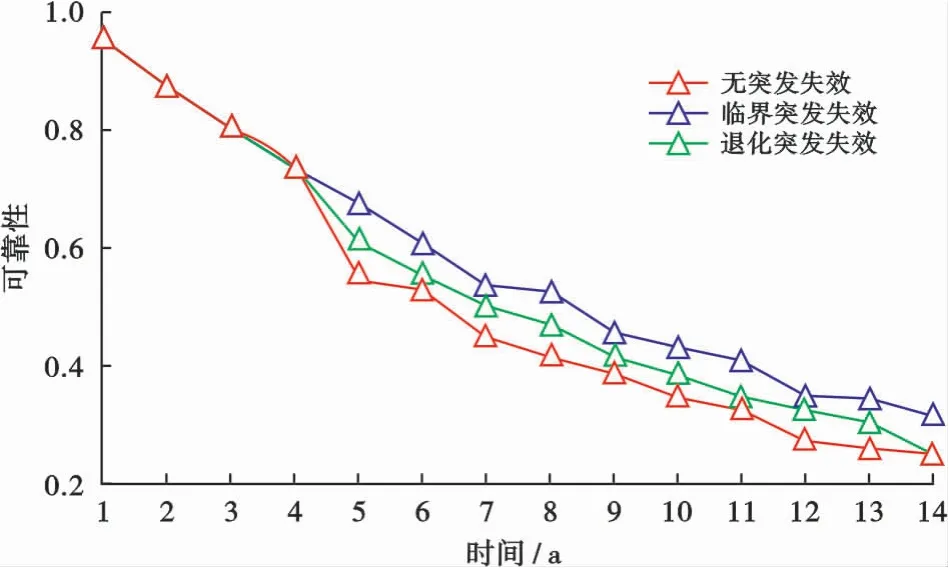
图6 不同突发失效模式FPSO的可靠性Fig.6 Reliability of FPSO under different sudden failures

3.2 考虑相互依赖性的水下采油树贝叶斯网络模型

当建立好FPSO突发失效情况下的可靠性模型后，要预测水下采油树系统整体可靠性变化，则需考虑水上部分、水下部分与FPSO的相互依赖性，并以水下采油树系统的电控部分为主线，建立考虑相互依赖性的水下采油树系统整体贝叶斯网络模型。

根据高文科等［15］建立的相互依赖性部件间影响关系，本文提出了针对水下采油树系统各组件间的相互依赖性关系：

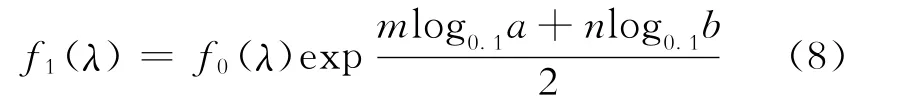
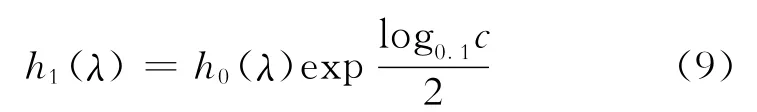
式（8）～（9）中：f1（λ）为突发失效后水上部分中电控部分的失效率；f0（λ）为水上部分电控部分前一时刻的失效率；h0（λ）为水下部分中电控部分前一时刻的失效率；h1（λ）为水上部分电控部分可靠性改变而引起的水下部分电控部分失效率的变化；m、n分别为水上部分、水下部分与FPSO的相关系数，根据水下采油树系统实际情况，分别定义m=0.6、n=0.4；a为发生突发失效时水下部分的可靠性；b为发生突发失效后FPSO的可靠性；c为受FPSO突发失效影响后水上部分的可靠性。

建立考虑相互依赖性的贝叶斯网络模型时以无相互依赖性的模型为基础，同样假定在第4 a时FPSO发生突发失效，则前3 a各模块及总体的可靠性不发生变化，将第4 a水下部分模块可靠性原始节点和修改参数后的FPSO的可靠性节点作为该建模过程的父节点，并引入2个新的变量节点“lamuda”“lamudaa”，分别作为新时刻水上部分、水下部分电控部分的λ值，完成建模。

突发失效下考虑相互依赖性的水下采油树整体贝叶斯网络模型如图7所示。将该模型继续扩展6～7 a，则可获得突发失效情况下考虑相互依赖性的水下采油树系统可靠性随时间的变化曲线。

3.3 考虑相互依赖性的可靠性及剩余寿命

根据突发失效下考虑相互依赖性的水下采油树整体贝叶斯网络模型，可以得到临界突发失效和退化突发失效下水下采油树系统各模块及整体的可靠性变化规律，如图8所示。可以看出，在2种突发失效模式下，水下采油树系统可靠性变化曲线的总体变化趋势一致；与临界突发失效比，退化突发失效的水上部分可靠性更快地降至FPSO可靠性以下；2种突发失效模式的整体可靠性在第10 a均已接近于0。

图8 临界突发失效和退化突发失效下考虑相互依赖性的水下采油树系统可靠性Fig.8 Reliability of subsea Christmas tree system with critical failure and degradation failure by considering interdependence

对比图8和图3可知，在同一时刻下，考虑相互依赖性系统各模块的可靠性均有不同程度的降低，且整体可靠性比无相互依赖性的情况提前了接近2 a；考虑相互依赖性的水上部分模块可靠性下降变化最为明显，其降低速率随时间不断增大，而考虑相互依赖性的水下部分模块可靠性变化不大。这一结果的产生主要包括2个原因：一是水上部分模块与系统其他部分联系最为密切；二是水下部分只与水上部分存在相互依赖性，与水下采油树系统其他组成部分联系较少。也就是说，相互依赖性关系的复杂程度决定了系统内部甚至整个系统可靠性的变化，并在剩余寿命预测中起到了至关重要的作用。

选取与无相互依赖性贝叶斯网络模型相同的失效阈值（0.1），考虑相互依赖性的不同失效模式下水下采油树系统剩余寿命预测如图9所示。可以看出，随着无突发失效、临界突发失效和退化突发失效冲击强度的增大，各模块的剩余寿命均有所降低；相互依赖性关系多的水上部分模块，其剩余寿命所受影响的程度较大，水下部分次之；FPSO的剩余寿命随冲击强度的增大而减少，但由于该部分与系统的相互依赖性较弱而变化并不明显；系统整体的剩余寿命显著减少。

图9 不同突发失效模式下考虑相互依赖性的水下采油树系统剩余寿命Fig.9 Remaining useful life comparison of subsea Christmastree system under different sudden failure modes

对比图9和图4可知，高强度的突发失效将使系统失效过程加速，进而减少设备的剩余寿命，考虑相互依赖性的设备剩余寿命明显低于不考虑相互依赖性时的设备剩余寿命。

3.4 失效阈值的敏感性分析

由于剩余寿命预测中失效阈值的设定一般通过实际情况和专家经验等方法确定［14］，存在一定的主观性，因此有必要对失效阈值进行敏感性分析。以考虑相互依赖性的水下采油树系统整体为对象，将其失效阈值分别设置为0.06、0.08、0.10、0.12和0.14计算相应的剩余寿命，结果如图10所示。可以看出不同失效阈值对剩余寿命存在一定的影响，但与初始失效阈值0.1对比，所预测的剩余寿命值均在±20%以内浮动，因此从工程的角度出发认为，水下采油树系统剩余寿命对失效阈值的敏感性较弱。

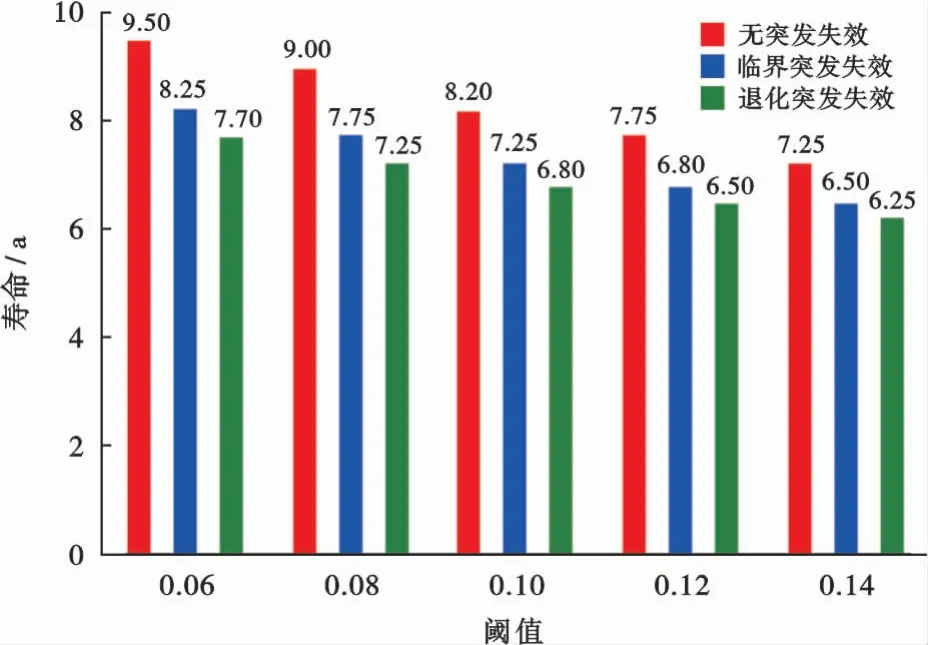
图10 不同失效阈值的水下采油树系统整体剩余寿命Fig.10 Remaining useful life of subsea Christmas tree system with different failure thresholds

4 结论

1）采用考虑水下采油树系统各模块相互依赖性关系的建模方法，结合贝叶斯网络模型，可以得到可靠性退化曲线，并可以进一步预测水下采油树系统的剩余寿命。

2）水下采油树系统的水下部分和FPSO共同影响水上部分的可靠性变化，而随着水上系统可靠性变化过程进一步影响了水下部分的可靠性；整体可靠性低于其任一模块的可靠性，其退化过程先快后慢，大体呈指数分布；水下部分由于所处环境恶劣，同一时刻内相较于水上部分及FPSO，有着较低的可靠性。

3）高强度的突发失效会加速系统的失效过程从而减少设备的剩余寿命，考虑相互依赖性的设备剩余寿命明显低于不考虑相互依赖性时的设备剩余寿命。