富水深基坑降水引起的地表沉降预测
江 杰, 魏 丽, 胡盛斌, 钟有信, 杨杉楠
(1.广西大学土木建筑工程学院,南宁 530004;2.南宁轨道交通集团有限责任公司,南宁 530029)
随着城市建设的发展,轨道交通已在各大城市中得到合理利用。对地下空间的开发也推进了深基坑工程的发展。在地下水丰富的地区必须采用降水措施以保证基坑开挖面的干燥作业,而降水过程对土体应力重分布造成的影响导致地面产生沉降,由此引发的工程问题时有发生并引起广泛关注[1-4]。因此,合理地预测由基坑降水过程引起的地表沉降就显得尤为重要。
基坑降水使原有地下水位发生变化,改变了周围土体的应力分布,从而引起地面沉降。为研究基坑降水引起的地面沉降问题,许多学者做了大量的研究工作。陈学根等[5]和黄显贵等[6]认为降水使基坑水位面以下的土体有效自重应力发生变化,从而导致周围土体的沉降;曾超峰等[7]发现土的渗透特性对被降水土层的孔隙水压力也会产生不同程度的影响,透水层之间发生水的渗流从而引起更强的应力重分布;谷拴成等[8]和施成华等[9]提出降水使土体内部的水产生流动,并将其假定为一维竖向渗流,并结合渗透力引起的有效应力变化对土体竖向沉降进行计算;郑刚等[10]认为基坑预降水造成围护结构周围土体应力状态发生改变,从而产生坑外土体变形;李琳等[11]认为基坑围护结构对降水引起的土体沉降有约束影响,并利用剪切位移法对约束位移进行了计算。以上学者分析了基坑降水对土体应力分布产生的变化,并引入到地表沉降计算中,但影响因素考虑比较单一,且地下水渗流作用仅假设为一维竖向渗流,应用到富水地区的基坑工程地表沉降预测中存在着较大的误差。
研究基坑降水过程土体的自重应力变化,同时将地下水渗流假定为二维渗流,计算渗透力在与土体沉降一致的竖直方向产生的附加应力变化,由此分析这两者的应力叠加效应对地表沉降产生的影响。同时进一步考虑基坑降水期间止水帷幕与土体间摩擦阻力对土体沉降的约束作用,并建立了基坑降水地表沉降计算公式。最后,应用工程实例进行计算和分析,验证理论计算方法的正确性。
1 降水前后有效应力变化引起的地表沉降
1.1 土体自重应力变化引起的地表沉降
根据太沙基有效应力原理,土体自重应力是土的自身有效重力引起的,不完整井基坑内降水时,基坑内外水力联系无法完全阻断,降水导致基坑周围水位下降,从而使土体自重应力增大,这些附加应力引起了地表沉降。如图1所示,设初始地下水位位于地表以下h0处,降水前土层含水厚度为H,基坑坑内降水产生坑内外水头差,在基坑外形成降水后的地下水位曲线f(x)。
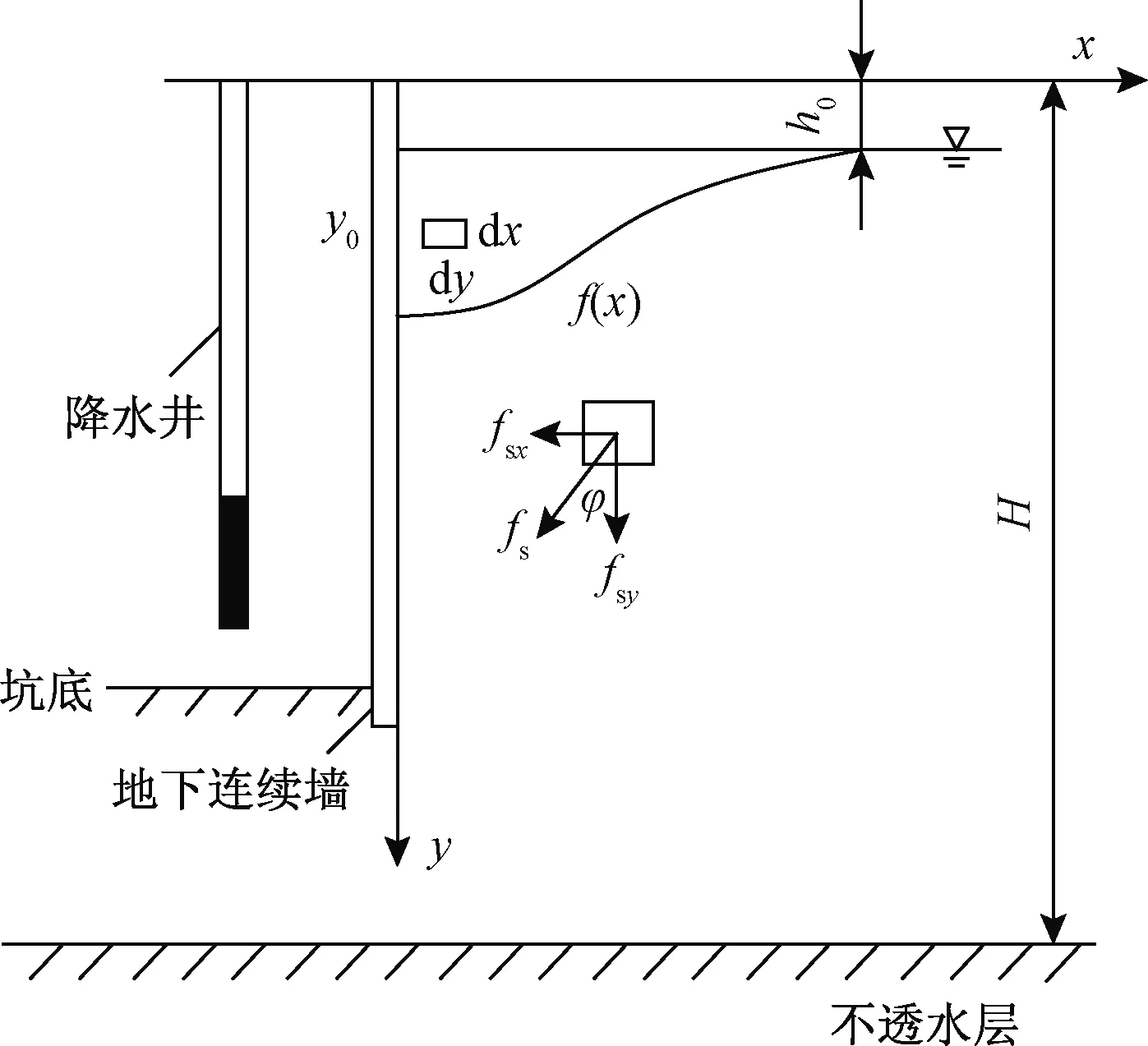
图1 基坑降水示意图Fig.1 Schematic diagram of foundation pit dewatering
在地面线与初始地下水位线之间,由于不产生土体的降水疏干,因而在该区域内有效应力没有变化,沉降可忽略不计。初始地下水位线以下土体内的孔隙水因降水被疏干,土骨架承担的应力随之增大,从而使有效应力增加,产生土体沉降。将初始水位线以下的土体以坑外降水曲线f(x)为界分为两部分,降水曲线以上的为疏干区,降水曲线以下的为饱和区。
设地下水降至y0处,达到稳定状态。在y0处有一微单元体dxdy,应力为σ,孔隙水压力为uw,则降水前该单元体所受有效应力为
σ′1=σ-uw=h0γ+γ′(y0-h0)
(1)
式(1)中:γ为土体天然重度,kN/m3;γ′为土体有效重度,kN/m3。
降水后,y0处的水被疏干,微单元体所受有效应力为
σ′2=γy0
(2)
则单元体在降水后的有效应力增量为
ΔσΙ=σ′2-σ′1=(γ-γ′)(y0-h0)=
γw(y0-h0)
(3)
式(3)中:γw为水的重度,kN/m3。
降水曲线以下的土体在降水后的有效应力增量为
ΔσⅡ=γw[H-f(x)]
(4)
降水引起土体自重应力变化而产生的有效应力增量为
Δp1=ΔσΙ+ΔσⅡ
(5)
f(x)为不完整井基坑降水曲线[12],表示为
(6)
式(6)中:h为距地连墙x处土层的含水厚度,m;hw为降水稳定后坑外距地连墙最近的含水层厚度,m;k为土层渗透系数,m/d;Ha为基坑内不完整井降水有效影响深度,m,可以根据式(7)取值。
(7)
式(7)中:R为基坑降水影响半径,m;rw为降水井半径,m;sw为水位降深,m;l为降水井过滤器长度,m。
由于基坑初始地下水位一般在地表以下处,f(x)即表示降水稳定后坑外地下水位距地表以下h0处。故令基坑外水位曲线:
f(x)=h0+(H-h)=
(8)
因此,基坑降水后土体自重应力变化引起的地表沉降:
(9)
式(9)中:ψs为土的沉降压缩经验系数,一般按地区经验取值,无地区经验时一般取1;Ei为土的压缩模量,MPa。
1.2 地下水渗透力变化引起的地表沉降
基坑降水使坑内外产生水头差,从而引起周围地下水的流动。由地下水渗流理论可知,水流作用于土粒骨架的渗透力会造成土体中有效应力的变化。土体在渗流作用下有效应力增加,进而导致附加沉降。
假设地基土层为均质土,基坑降水引起的渗流做平面运动,即平面二维渗流。如图1所示,在降水曲线以下土体的渗流场中沿流线方向任取一微分体,水流对土粒骨架作用一单位渗透力fs,计算式为
fs=γwJ
(10)
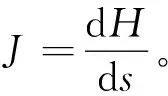
(11)
cotφ即为降水稳定后微分体中点[x0,f(x0)]处水位线的一阶导数f′(x0),即
(12)
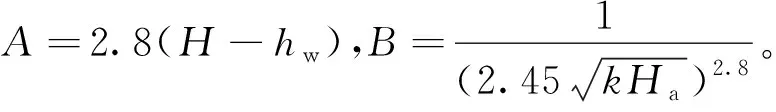
根据三角几何函数关系可得:
(13)
再由式(10)、式(13)得竖向单位渗透力fsy,即
(14)
地下水位线以下的微分体由渗流动水压力作用而在竖直方向上产生有效应力增量Δp2,其计算式为
Δp2=fsy[y-f(x0)]
(15)
则渗透力在竖直方向上产生的有效应力变化所引起的地表沉降:
(16)
2 止水帷幕对地表沉降的约束影响
在地下水位丰富的地区进行基坑施工时,为防止基坑降水困难,在降水前很多工程都需要设置止水帷幕阻断基坑内外的水力联系,以防止地下水的渗漏。基坑止水帷幕与周围土体之间产生摩擦阻力,该阻力在一定范围内对土体下沉产生约束,从而减小了坑外地表沉降。
忽略止水帷幕因自身施工产生的位移变化,并认为其是固定不动的。如图2所示,假定止水帷幕对土体沉降的约束范围为一倍的降水深度,即H0。那么在约束范围内,因降水产生的应力增量形成止水帷幕与土体间的摩擦阻力,进而使交界面处产生向上的剪切应力τ0。在离开止水帷幕范围内,摩擦阻力缓慢衰减,产生的剪应力为τ,至距止水帷幕1倍降水影响深度处衰减为0。假定止水帷幕与周围土体发生的剪切变形为弹性变形,那么剪应力应遵循与摩擦阻力相同的衰减规律。
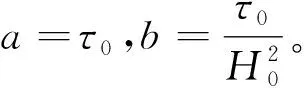
(17)
降水引起土体自重有效应力和渗透力产生应力增量,这两部分增加的应力即为止水帷幕与土体交界处产生剪应力τ0,其计算式为
τ0=Δp1+Δp2
(18)
利用剪切力τ与剪应变γ的关系,即可求出降水期间土体剪切变形引起的竖向位移,其计算式为
(19)
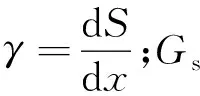
在距止水帷幕x处由单元土体剪切力τ所引起的竖向位移Sτ可由式(20)求得,即

(20)
式(20)中:0 通过以上分析可知,基坑降水会引起土体自重及地下水渗流产生的应力叠加,这两部分有效应力的增加都会对坑外的地表沉降产生影响。此外,止水帷幕因降水与土体之间产生摩擦阻力,周围土体也随之发生向上的剪切变形,对地面沉降产生一定范围的约束影响。因此,坑外土体因基坑降水而产生的沉降可表示为 sw=s1+s2-sτ (21) 南宁市轨道交通5号线广西大学站基坑长156 m,标准段宽度22.1 m,基坑开挖深度为26.53 m。基坑支护采用兼有止水帷幕功能的直径1 000 mm的地下连续墙加内支撑支护方案,并配合采用基坑内降水措施。降水井采用内径400 mm的钢管抽水,过滤水管的工作长度为12 m。场地范围内主要揭露第四系及古近系地层,各岩土层物理力学指标如表1所示,各土层泊松比相差不大,统一取0.25。场地勘察期间初见水位平均埋深8.8 m,多赋存在黏性土及粉土中,圆砾层中稳定水位埋深在7.80~11.30 m。基坑先降水后开挖,基坑降水需将地下水位下降至基坑底板以下1 m处,最大水位降深19 m。基坑降水半径可用式(7)求得,约为300 m,降水影响深度为35.4 m。 表1 各土层物理力学指标Table 1 Physical and mechanical indexes of each soil layer 为确保基坑降水工程的顺利进行和周边环境的安全,准确反映坑外降水效果及其地表沉降大小,在基坑内部南北两侧共布置10口降水井进行坑内降水,周围布置排水沟,将水汇入集水井。同时对基坑周边一定范围内布置监测点对各个监测点的沉降观测值进行监测。计算断面选取标准段断面1—1及其附近的7个地表沉降监测点,按平面应变问题进行分析。各监测点到基坑支护结构边缘距离由近及远分别为4.72、8.72、12.72、16.72、20.72、24.72、28.72 m,具体位置如图3所示。 图3 监测断面及测点布置图Fig.3 Layout of monitoring sections and measuring points 基坑降水引起地表沉降的传统算法是只考虑降水前后自重应力引起的有效应力变化,这里还考虑了渗流动水压力在竖直方向上的有效应力变化影响。此处选择实测点D1、D3,分析其在传统算法和本文算法中有效应力变化的不同,对比如图4所示。 图4 降水前后有效应力对比Fig.4 Comparison of effective stress before and after precipitation 由图4可以看出,考虑降水后自重应力变化和竖向渗流所产生的有效应力较降水前增大15%左右,而渗流产生的有效应力增大了5%左右,可见,基坑因地下水渗流增大的这部分有效应力是不可忽略的。因此,将地下水渗流在竖直方向上产生的影响考虑到降水有效应力变化中是很有必要的。 根据以上工程条件可以得出在该工程背景下的坑外地表沉降,依据理论公式计算的结果与实测值和传统算法计算结果的对比如表2和图5所示。 表2 理论计算与实测对比Table 2 Comparison between theoretical calculation and actual measurement 图5 坑外地表沉降曲线对比Fig.5 Comparison of surface settlement curve outside pit 由表2中的数据看出,理论计算结果与实测值各点之间的相对误差不超过12%,从而验证了本文方法可以更准确地描述实际基坑坑内降水引起坑外地表沉降的趋势变化。 由图5可以看出:①传统算法的计算值要明显小于工程现场监测点的实测值,这是因为传统算法并没有考虑到竖向渗流动水压力对土体沉降的影响,可见地下水渗流作用对土体沉降产生的影响是不容忽视的;②考虑止水帷幕约束作用的理论计算曲线在距基坑边缘17 m范围内与实测数据拟合较好,在计算假定的约束范围内且相差不大,说明止水帷幕对土体沉降的约束主要作用在距支护结构边缘约一倍降水影响深度范围内;③所提出的考虑自重应力变化、竖向渗流动水压力和止水帷幕约束这三者的变化影响要比只考虑前两者更接近实测数据,理论计算曲线与实测值的变化趋势也较为一致。 研究了基坑坑内降水导致坑外地表沉降的机理,提出简化计算方法,利用该方法对某工程实例进行计算,对比理论计算和实测结果,得到以下结论。 (1)本文的公式适用于不完整井基坑降水引起的地表沉降计算。通过本文方法计算由降水引起的地面沉降,可以综合考虑土体自重应力、竖向渗透力变化和止水帷幕约束作用等因素的影响,理论计算曲线与实际监测数据走势吻合,计算结果能较为准确地反映基坑坑内降水对坑外土体的影响变化,因素考虑更为全面。 (2)将渗流动水压力作用简化为二维平面问题,其在流线竖直方向上的分量所产生的有效应力比传统算法增大了5%,并将该部分增大的有效应力代入到土体竖向沉降计算中,使计算结果更为精确。 (3)止水帷幕对土体沉降的约束影响在距基坑支护结构边缘1倍降水影响深度范围,因此,在该范围内计算地表沉降时需将止水帷幕的约束影响考虑在内。 (4)利用本文的理论公式计算得到的结果与实际工程的监测数据对比,误差均在12%以内,这在一定程度上证实了该计算方法的可靠性。同时可利用理论公式后续曲线的发展情况对地表沉降进行预测,为地铁基坑降水工程可能存在的风险提前做出预警。3 总地表沉降量计算
4 工程实例计算分析
4.1 工程概况


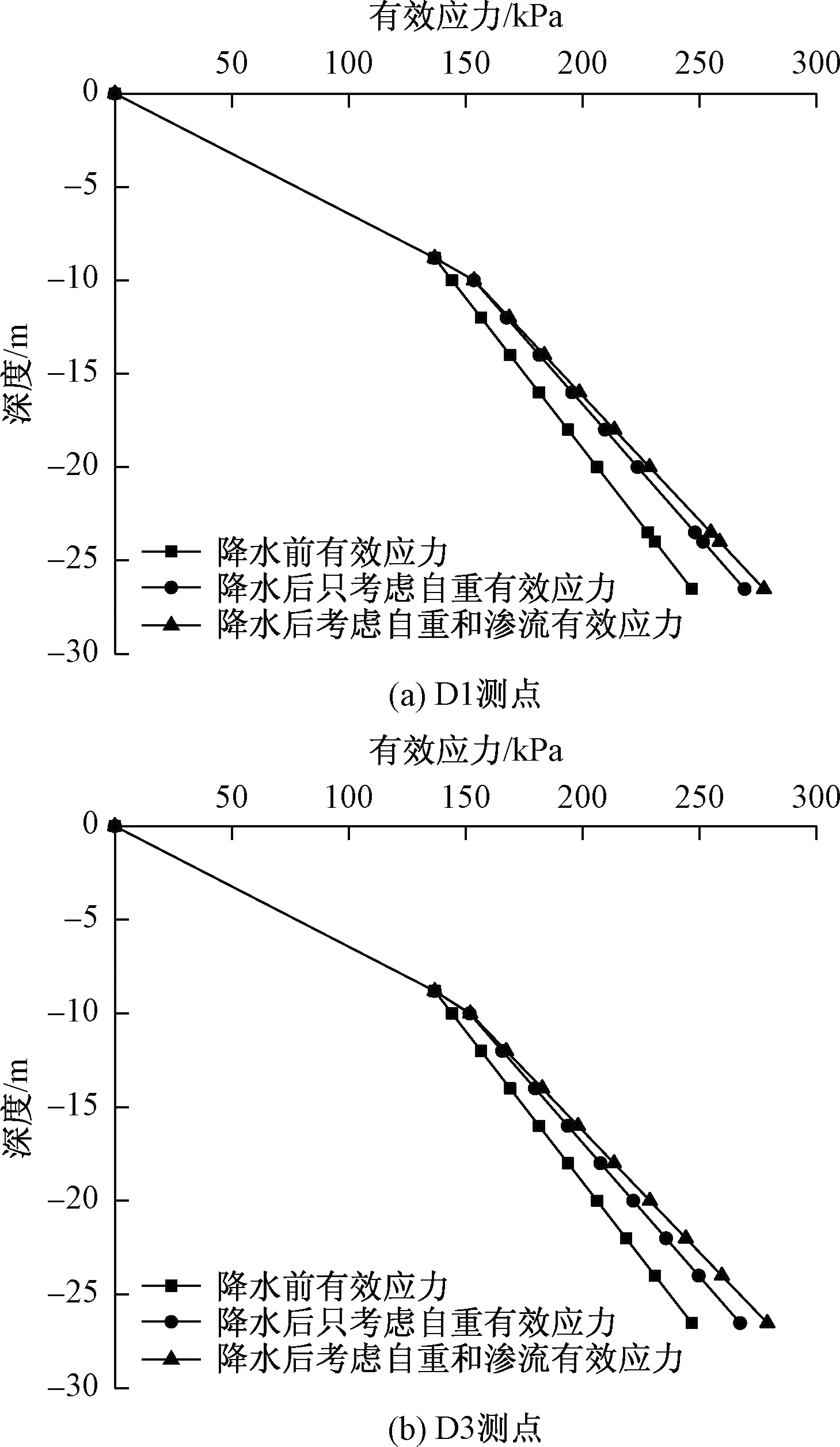
4.2 有效应力计算结果
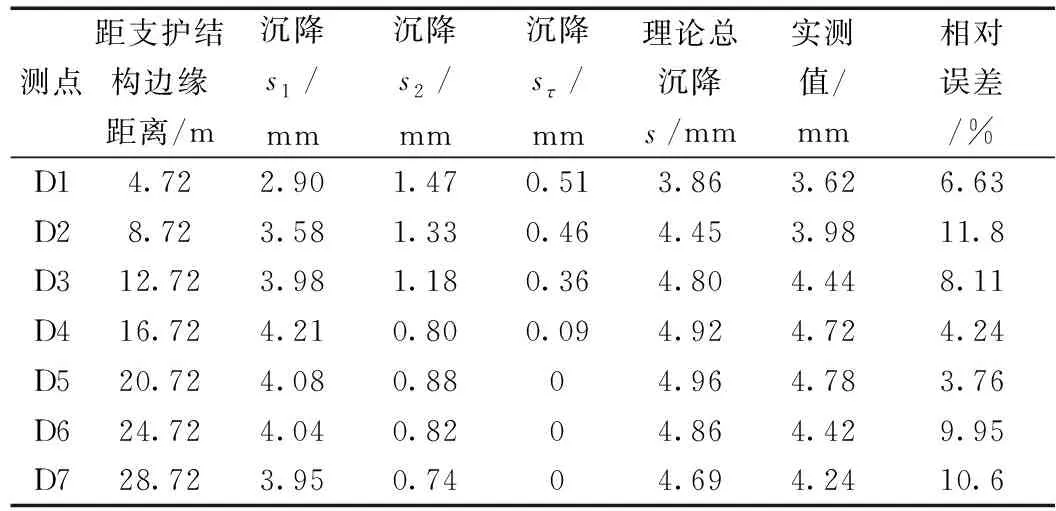
4.3 沉降量计算结果

5 结论

