风荷载作用下输电线路数值模拟及金具失效分析

刘小会, 周晓慧， 叶中飞， 伍 川， 张 博， 黄 飞

(1.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074；2.重庆交通大学土木工程学院,重庆 400074；3.国网河南省电力公司电力科学研究院输电线路舞动防治技术重点实验室,郑州 450052)

近年来,风荷载作用下架空输电线路金具失效断裂问题越来越引起人们的关注[1-2]。金具失效会导致输电线路导线脱落、回路跳闸等故障,严重威胁电网系统的安全运行[3]。针对金具失效分析的研究逐渐引起中外科研工作者的重视。然而由于整体结构极其复杂,多数学者集中于研究局部的连接金具,对于电力金具整体结构的有限元仿真研究几乎是空白。例如：逯平平[4]、杨现臣[5]研究了新疆地区强风环境下电力金具U形挂环磨损行为；韩哲文等[6]分析了球头挂环和连接螺栓疲劳断裂失效原因；汪旭旭等[7]通过建立不同工况下地线悬吊金具简易受力模型,分析磨损情况和影响因素。这其中针对局部情况的研究均以现场的实际破坏结果作为研究依据,缺乏理论性和系统性的指导。针对输电线路连接金具系统性的分析研究,可为电网系统的运维工作提供有效的理论依据。

为缓解目前由于风荷载影响造成输电线路金具失效断裂等问题,保障电网系统安全运行,建立输电线路连接金具的整体装配模型有限元模型,对两种典型荷载工况下金具应力情况进行系统性分析及局部受力情况对比,找出危险金具及易损点,为输电线路运维工作提供方向性的理论指导。

1 高压输电线路力学模型

1.1 整体输电线路有限元模型

以220 kV辛安—肖城线路工程为背景,选取特征段线路作为研究对象。如图1所示,特征段线路总跨度591 m,档距包括l1=295 m,l2=296 m,杆塔呼称高h依次为21、42、42 m。

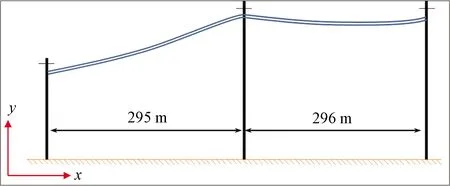
图1 特征段线路示意图Fig.1 Schematic diagram of characteristic circuit

通过ABAQUS有限元分析平台,建立图2所示的两档双分裂导线有限元模型,通过模拟脉动风作用下输电线路动力响应计算导线应力。其中绝缘子串与连接金具整体总高度H0=1.25 m,导线选用JL/G1A-400/35钢芯铝绞线,具体参数如表1所示。每相导线双分裂,分裂间距为0.45 m。整体连接金具十分复杂,而此过程主要是通过分析输电线路动力响应计算作用在金具上的风荷载,因此将整体连接金具等效为三维桁架单元,单元类型为T3D2；导线选用三维桁架单元,单元类型为T3D2；间隔棒选用梁单元,单元类型为B31。有限元模型一共包括462个结点以及11个梁单元和401个桁架单元。

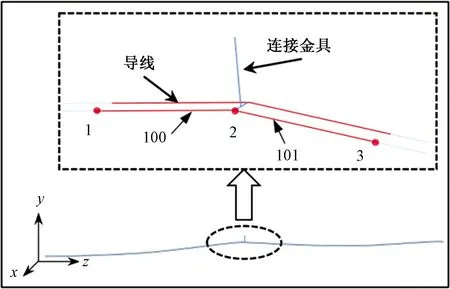
图2 特征段线路有限元计算模型Fig.2 Finite element calculation model of characteristic circuit

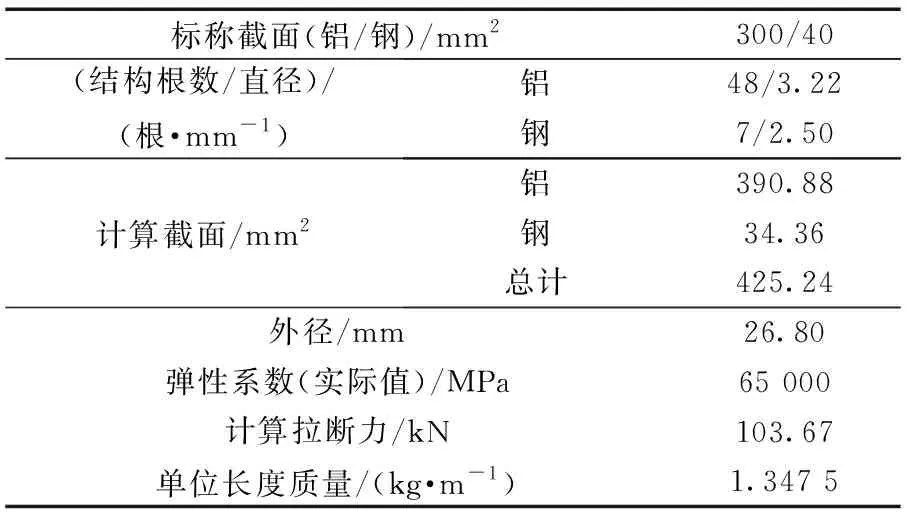
表1 JL/G1A-400/35钢芯铝绞线参数Table 1 Parameter of JL/G1A-400/35Steel cored aluminum strand

1.2 基于随机风的风荷载计算

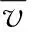
(1)

对于风速时程模拟主要是针对脉动风的模拟。功率谱和相关函数可以用于描述脉动风速特性,功率谱反映的是不同频率成分所对应的能量分布规律,相关函数反映位于不同时间或空间点之间的相互影响关系。各国学者提出了众多的脉动风功率谱,这里采用Kaimal提出的沿高度变化的风速谱:[11]

(2)

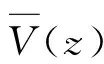
对于随机风荷载模拟主要有两类方法:一是线性滤波法,另一类是谐波叠加法。谐波叠加法具有较高的精度和效率,在研究领域中被广泛使用。现采用谐波叠加法模拟风速,它具有如下形式：

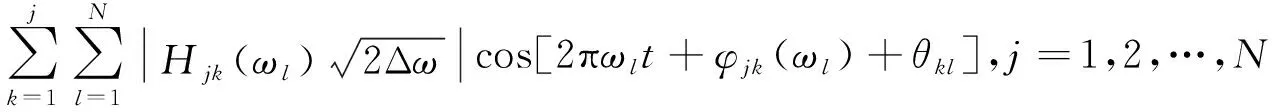
(3)

(4)

(5)

(6)

式中:ωu、ωk分别为频率上、下限；Δω为频率增量；N为频谱分割数,取正整数；θkl为0～2π范围内均匀分布的随机数；φjk(ωl)为两个不同点之间的相位角；Hjk(ωl)是由互功率谱密度函数矩阵S(f)按照Cholesky方法分解得到。根据Kaimal风速谱和Davenport互相关谱,利用快速傅里叶变换的谐波叠加法,通过MATLAB程序可以模拟得到沿输电线路方向多点互相关的随机风风速时程曲线及相关函数。

根据1.1节中特征段线路模型,为保证模拟样本覆盖整个输电线路的运行范围,如图3所示,每隔200 m模拟一个风速样本,选取模拟点坐标依次为A(0,21)、B(200,35)、C(400,42)、D(600,42)。根据当地气象资料,选取10 m高基本风速为27 m/s,地貌为B类,地面粗糙度系数α取0.16,地面粗糙长度z0取0.03[11]。频率等分数N=3 000,模拟时长为600 s,时间间隔为0.5 s,频率取值范围为0.003～1 Hz,频率增量为0.000 099 7。

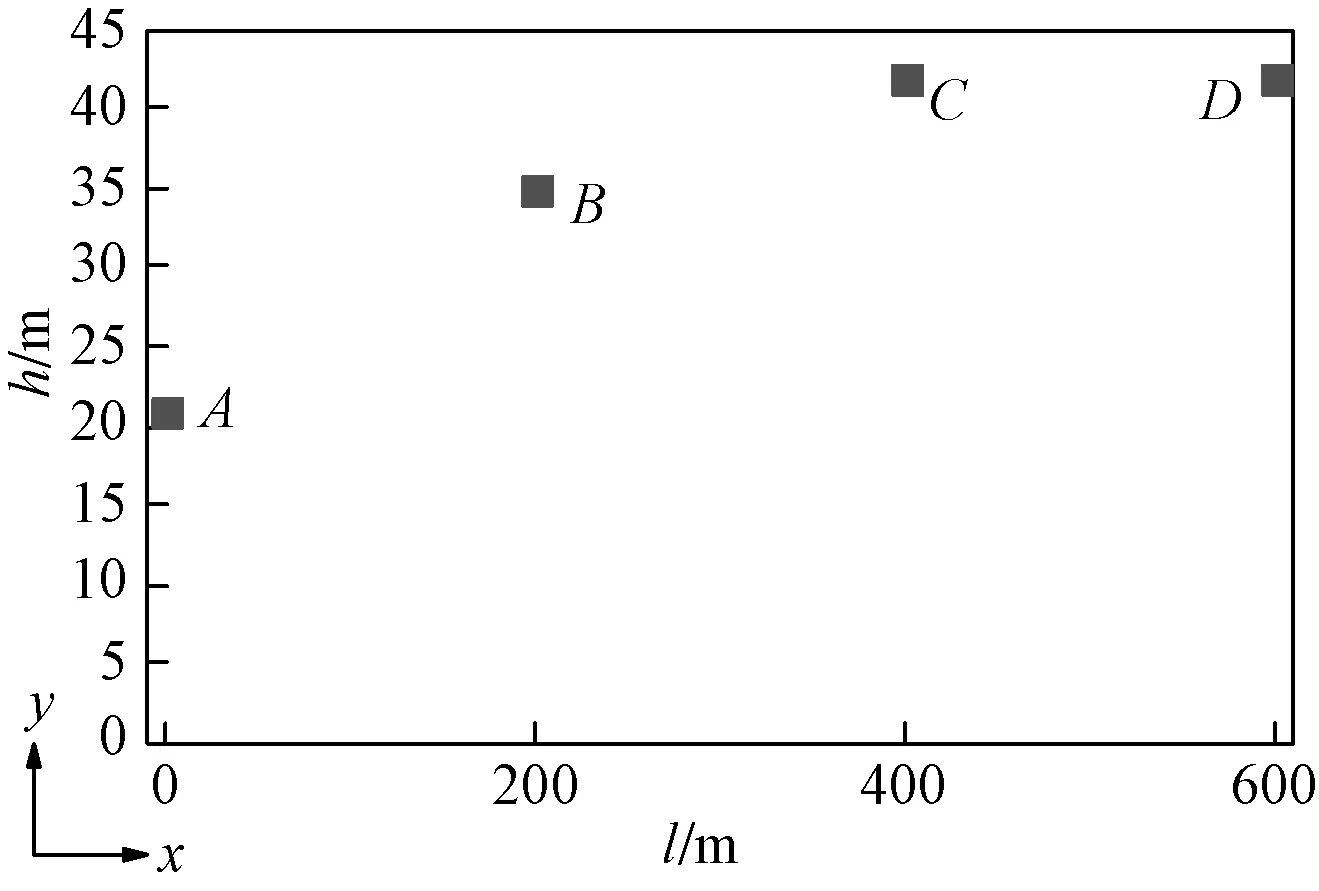
图3 风荷载模拟点坐标Fig.3 Coordinates of wind load simulation points

图4所示为A、D点脉动风速时程样本曲线。将模拟得到的风速时程曲线看成非周期函数,利用非周期函数的功率谱分析理论对模拟的脉动风速进行谱分析,如图5所示,从图像上可以看出模拟结果与理论值吻合较好。图6所示为A点自相关函数RAA(τ),A、B两点互相关函数RAB(τ),和A、D两点互相关函数RAD(τ),由结果可知距离越远相关性越差。通过数据分析,证明该数值模拟方法得到的风速时程样本合理。

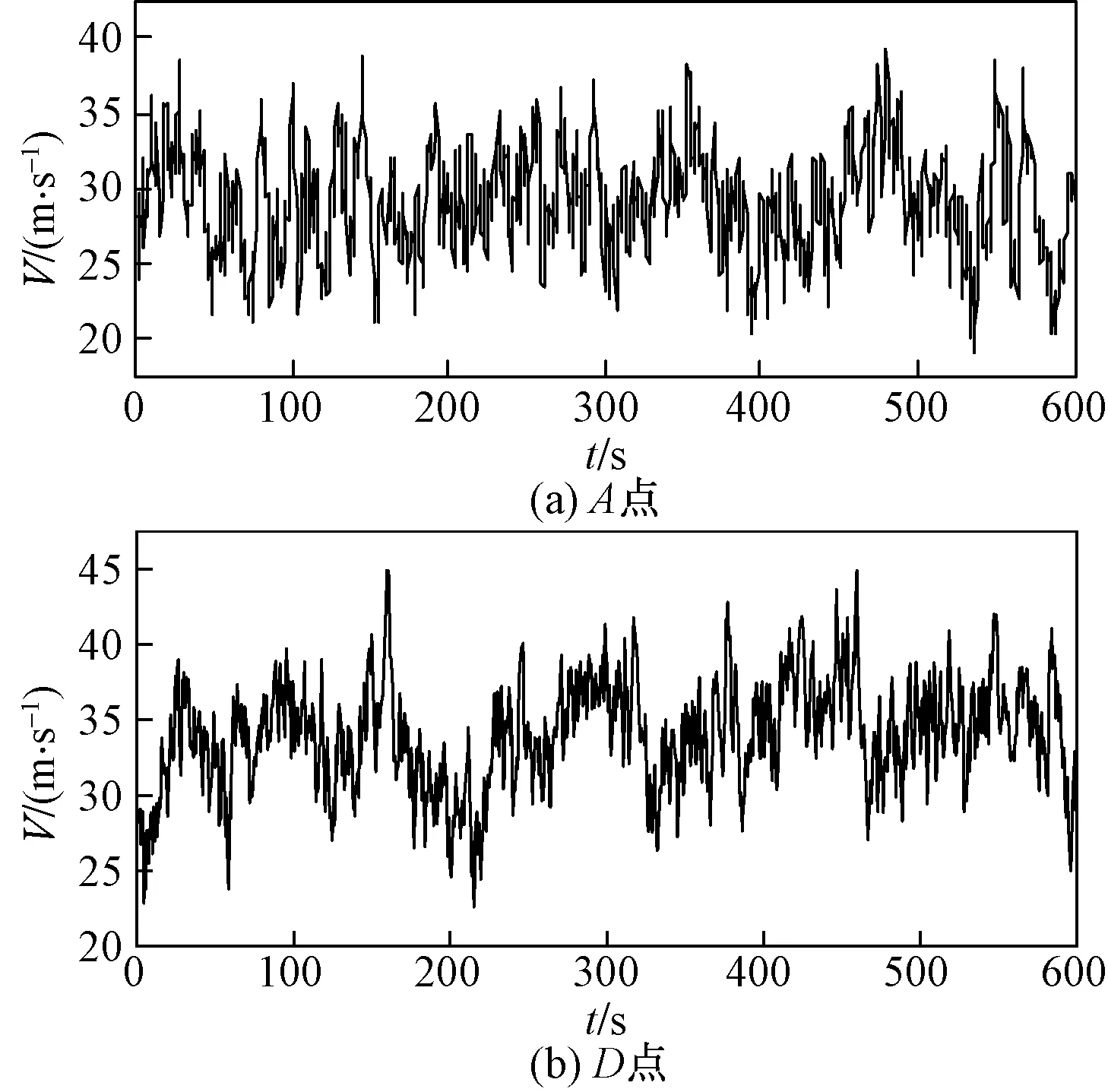
图4 A、D点随机风风速时程Fig.4 Time history of random wind speed at point A、D

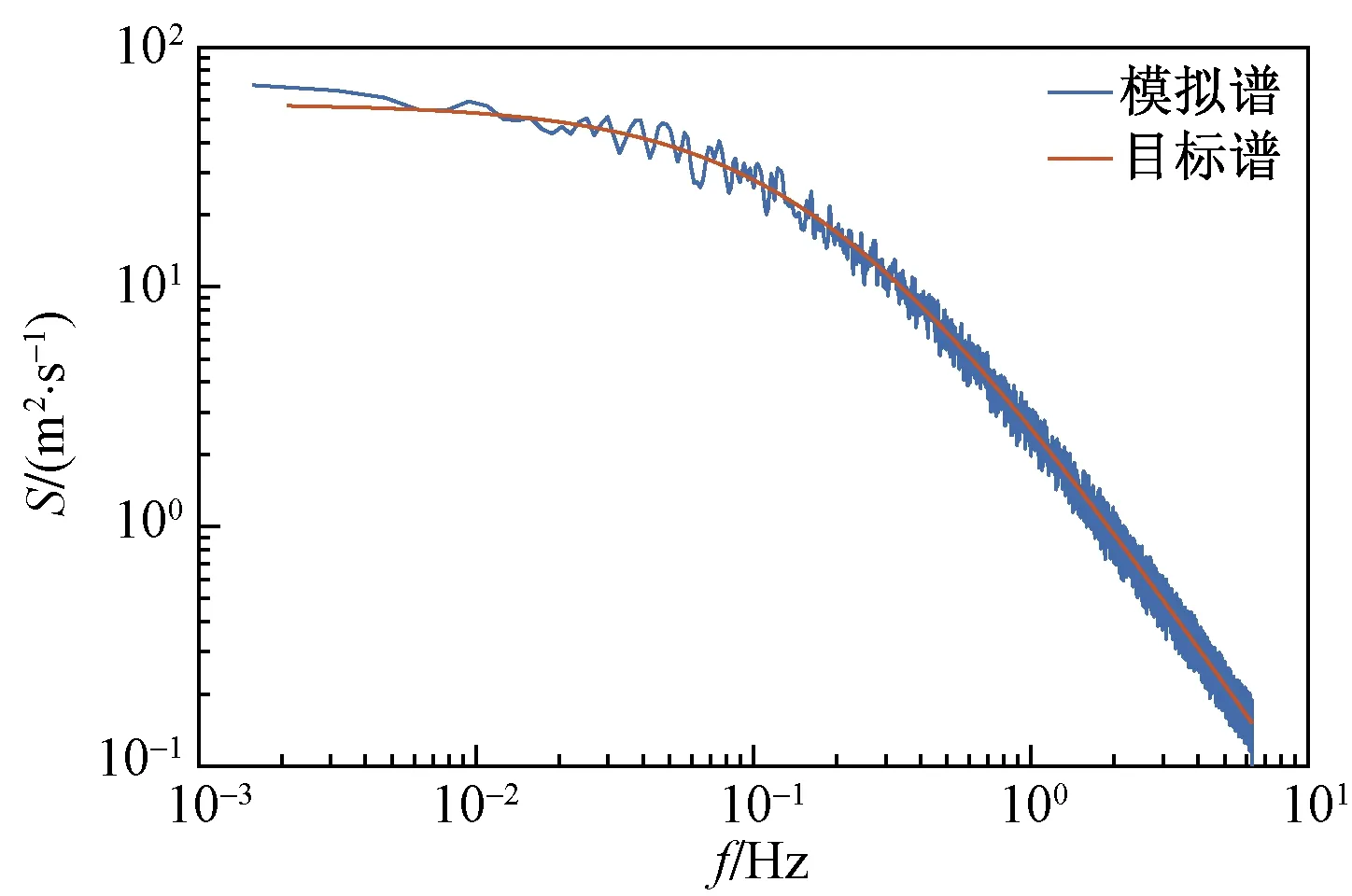
图5 A点功率谱函数与理论值比较Fig.5 Comparison of power spectrum function and theoretical value of point A

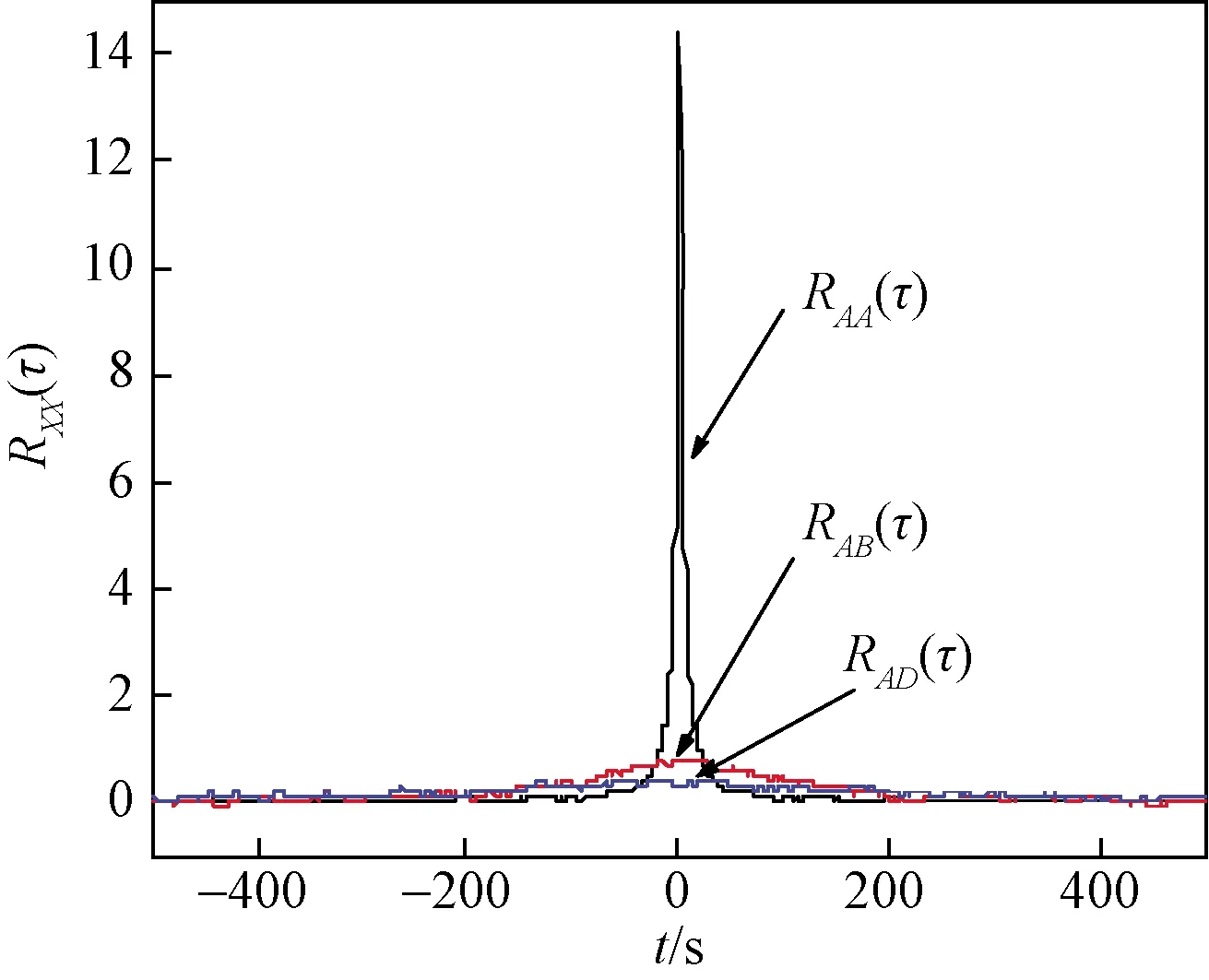
图6 模拟点风速的相关函数Fig.6 Correlation function of wind speed at simulation point

根据图3中有限元模型,该结构严格对称,则选择提取100单元和101单元应力σ,由公式：

F=σA

(7)

计算出风荷载作用在导线上的集中力F,式(7)中,A为导线截面面积，A=425.24 mm2,再通过1、2、3这3个结点变形后的空间位置坐标,建立三维坐标系,将导线的力等效为空间中沿x、y、z这3个坐标轴方向的集中力作用在金具模型上,再将100单元和101单元上3个方向的分量合成后可得出考虑脉动风影响时作用在金具模型上的3个方向的力,依次为顺风向的水平力Fx、竖直方向的力Fy、横风向的水平力Fz。图7所示为脉动风作用下顺风向与横风向的水平力Fx、Fz与时间的关系。顺风向风荷载明显大于横风向风荷载,导线会因为横风向风荷载的激励而来回摆动。

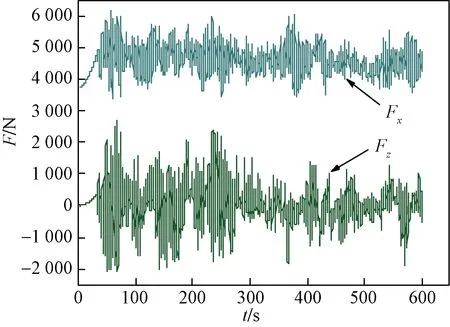
图7 随机风荷载Fig.7 Random wind load

1.3 基于稳定风的风荷载计算

不考虑脉动风荷载对输电线路的影响,作用导线上的水平风荷载可以用下列公式计算:

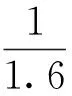
(8)

式(8)中:Wx为垂直于导线轴线的水平风荷载,N；α表示风压不均匀系数,根据设计基本风速v0=27 m/s取0.85；βc为500 kV导线及地线风荷载调整系数,仅用于计算作用在杆塔上的导线及地线风荷载,200 kV电压取1.0；μsc为导线和地线的体型系数,该模型导线外径大于17 mm,μsc取1.1；d为导线或地线的外径，mm；δ为导线覆冰厚度,mm,此研究不考虑覆冰；lH为杆塔的水平档距,m,该研究忽略高差对水平档距的影响,lH=(295+296)/2=295.5 m；θ为风向与导线或地线方向之间的夹角,(°),按最不利情况取90°；μz为风压高度变化系数,该场地为B类地面,离地面高度为42 m,通过线性插值取1.582；V为基本设计风速,根据当地气象条件取27 m/s。由此,作用在输电导线上的水平荷载Wx=[0.85×1.1×1.0×(0.026 8+0)×295.5×1.582×272×1]/(1.6)=5 337.25 N。

1.4 导线作用于线夹上的集中力

对比两种方法计算的风荷载,当考虑脉动风影响时,由于动力作用,将会产生横风向的水平力,顺风向的水平力比稳定风荷载大820.6 N,基于两种计算风荷载方法,选取两种荷载工况进行对比分析,工况1选取基于随机风作用下计算的最大荷载:Fx=615 7.85 N、Fy=-107 50.43 N、Fz=1 823.88 N,工况2选取基于稳定风计算风荷载、导线重力荷载及初始状态下导线横风向的水平荷载:Fx=5 337.25 N、Fy=-10 031.4 N、Fz=5.32 N。

2 有限元模型建立

2.1 几何建立

为了较真实地反映连接金具的受力情况,分别建立包括挂点金具、球头挂环、碗头挂环、直角挂板、复合绝缘子、联板、悬垂线夹、连接螺栓等不同连接金具的几何模型[12],再通过部件之间的位置约束装配为图8所示连接金具整体几何模型。

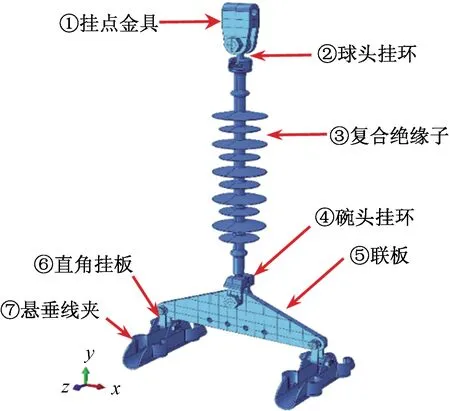
图8 连接金具几何模型Fig.8 The Geometric model of electric power fittings

2.2 本构模型

输电线路连接金具模型选用35号钢、35CrMo合金钢和Q345这3种型号的钢材,在ABAQUS属性模块中编辑材料的基本属性,其材料参数信息如表2所示。钢材塑性模型选用Varma模型及双折线本构关系模型,其屈服之后弹性模量E′s=0.01Es。

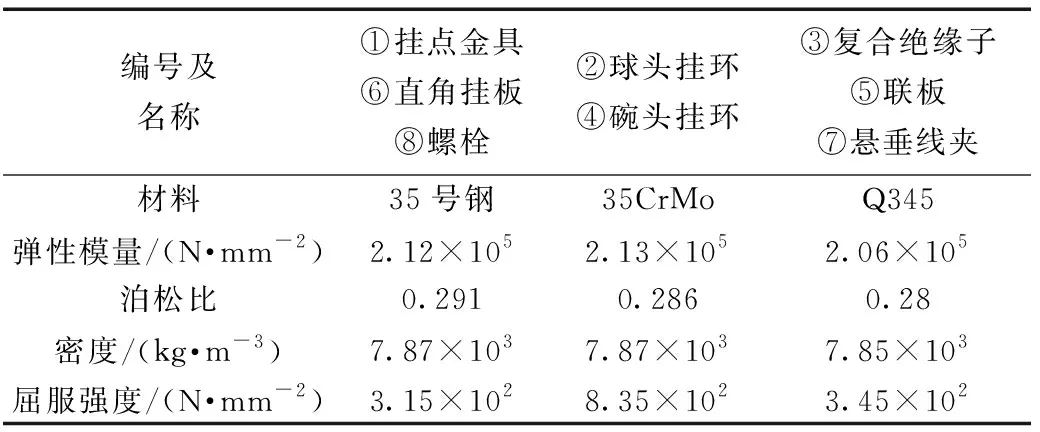
表2 模型材料参数Table 2 Material parameters of the model

2.3 连接关系

模型包括11种不同的部件,部件之间的连接关系十分复杂,用接触来建立相互作用关系难以实现,因此本模型在保证部件之间真实连接情况的前提下对部件之间相互作用的建立作相应简化。

模型有6个螺栓连接位置和2个球头球窝连接位置。在螺旋连接位置处作相应简化,通过tie将螺栓与其中一个金具进行绑定约束,相当于将螺栓和该金具简化为一个部件,然后分别在孔的中心位置分别建立两个参考点,通过coupling对两个部件进行耦合约束。对于球头球窝连接位置可利用相同方法直接将两个部件通过coupling进行耦合约束。

之后,对耦合的参考点创建连接线条wire,并赋予其连接属性。ABAQUS提供了丰富的连接截面类型,考虑其实际连接情况,如图9所示,在螺栓连接位置指定连接截面类型为“Hinge”,在球头球窝连接位置为球铰约束,自定义连接截面类型为“Jion+Flexion-Torsion”。模型一共包括6个“Hinge”连接截面和2个“Jion+Flexion-Torsion”连接截面。

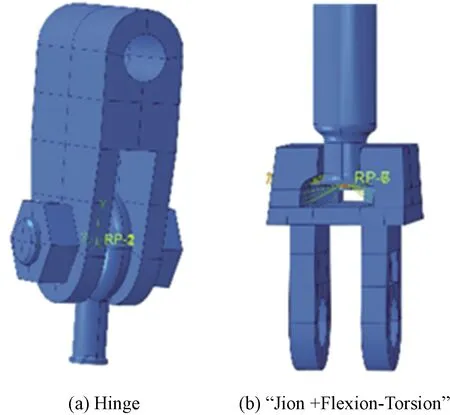
图9 连接截面类型Fig.9 Type of connection section

2.4 网格划分

有限元模型网格划分单元主要采用规则的六面体单元,在个别不允许选用六面体的复杂区域选用四面体单元代替,六面体单元类型选用C3D8R,四面体单元类型选用C3D10。整个有限元模型的金具结构特点差异比较大,球头挂环、U形挂环、碗头挂环及局部接触区域设置网格尺寸为2 mm,连接螺栓设置网格尺寸为3 mm,其余金具网格尺寸均设置为4 mm,该装配结构极其复杂,总的单元数量达到324 700个,其中包括323 659个六面体单元和1 041个四面体单元,有限元模型中金具网格如图10所示。

图10 金具网格Fig.10 Mesh of fittings

2.5 荷载及边界条件

如2.3节所述,考虑两种荷载工况,工况1中:Fx=6 157.85 N、Fy=-10 750.43 N、Fz=1 823.88 N,工况2中Fx=5 337.25 N、Fy=-10 031.4 N、Fz=-5.32 N。建立边界条件时,对悬垂金具顶端约束3个方向的平动以及绕y轴和z轴的转动,同时对连接处的参考点建立符合实际情况的转动约束。荷载及边界条件如图11所示。

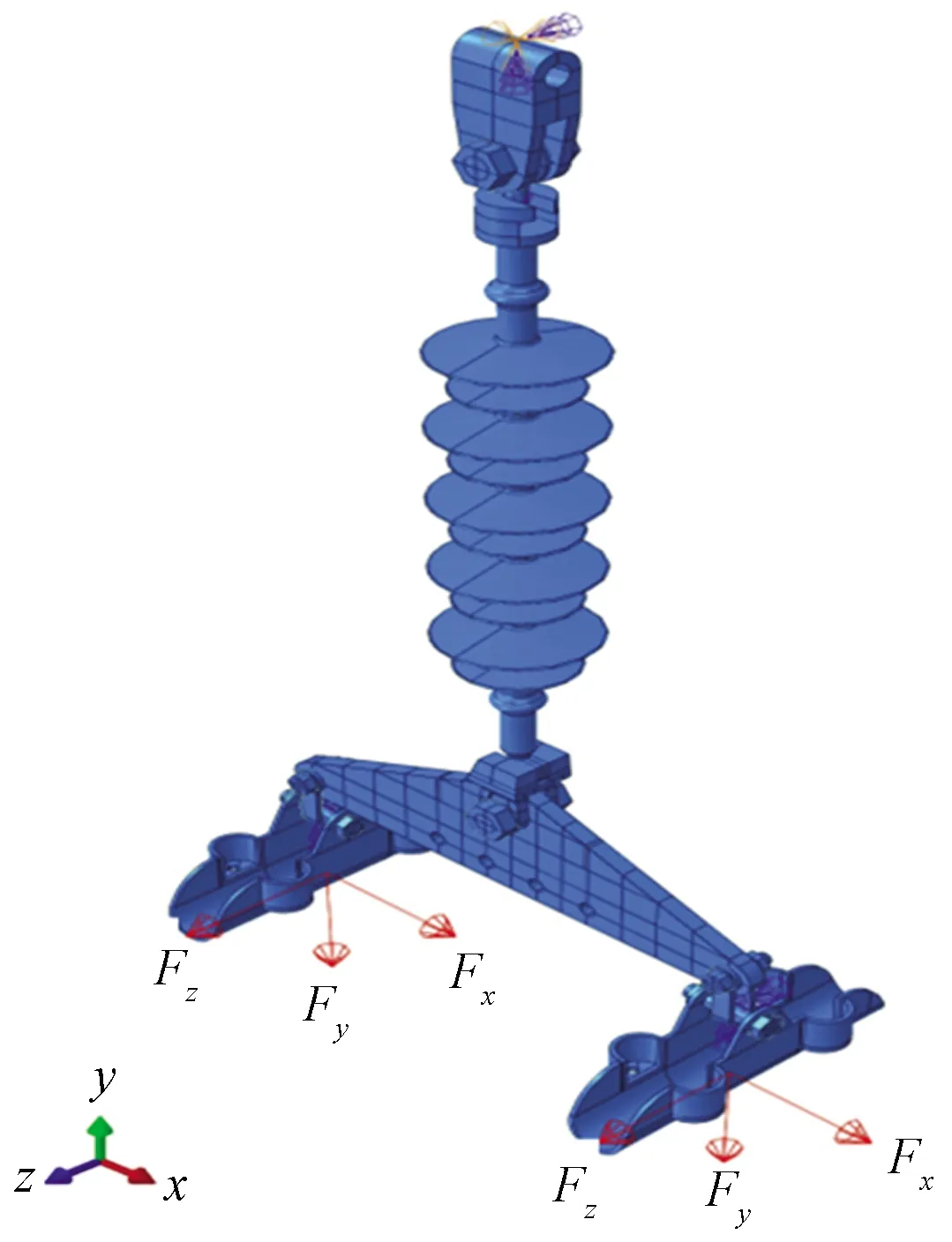
图11 荷载及边界条件Fig.11 Load and boundary conditions

3 风荷载作用下金具应力分析

3.1 整体模型应力场分析

连接金具整体变形及应力分布情况如图12所示,考虑风的脉动性影响分析所得最大应力为886.3 MPa,按稳定风荷载分析所得最大应力为820.1 MPa,两种计算情况最大应力相差66.2 MPa,可见动态风荷载对局部保护金具的影响值得引起重视。最大应力位置均出现在球头挂环圆环与球杆过渡处,该处由于几何结构发生改变,造成明显的局部应力集中,很有可能在风荷载作用下发生失效断裂。

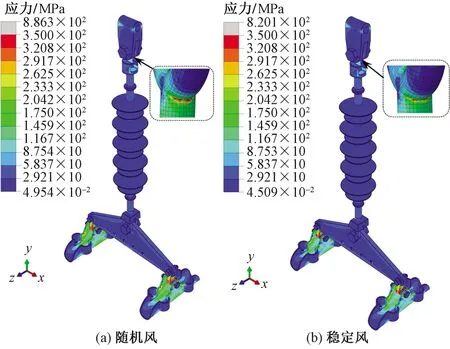
图12 整体应力分布情况Fig.12 Overall stress distribution

3.2 单个连接金具应力分析

两种荷载工况下,球头挂环应力分布情况几乎完全一致,如图13所示，在挂环的圆环与杆部过渡连接处由于几何形状,出现局部应力集中,在考虑脉动风荷载作用下,球头挂环圆环与杆部过渡处的计算应力已经超过了材料的屈服强度,工况2在此处最大应力为820.1 MPa,未达到材料屈服强度,可见动态风荷载对挂环有显著影响。

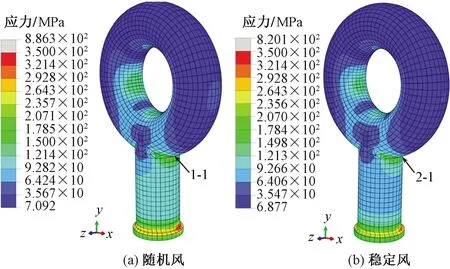
图13 球头挂环应力分布情况Fig.13 Stress distribution of ball head hanging ring

韩哲文等[6]对球头挂环断裂失效进行了实验研究和理论分析,断裂球头挂环宏观形貌如图14所示,并提出了风荷载为影响金具疲劳断裂的关键因素之一,但并没有在此基础上作有限元仿真分析。通过研究表明,有限元分析结果与工程实际情况相符,同时更加证明了风荷载对于球头挂环疲劳断裂失效的影响不容忽视,并且后续研究中应该在此基础上建立更精确的局部接触模型进行详细分析。在与复合绝缘子连接处,采用的球窝连接方式使球头挂环在轴向与横向的偏移程度非常有限,由于风荷载作用,在此处容易产生弯曲应力,在应力集中区域产生明显的应变,极易发生断裂破坏。针对以上情况,应在设计时考虑选用强度更高的材料或者改变几何结构形式。

图14 球头挂环断裂情况Fig.14 Fracture of ball head hanging ring

复合绝缘子整体应力相对偏小,如图15所示，从局部情况来看,在球杆拐角处表现出较大的应力,如上所述,此处同样为球头球窝连接处,是金具结构的薄弱环节,极易产生较大的双向弯曲交变应力。图16所示为实际勘察现场绝缘子球头断裂情况,分析表明,有限元模拟结果与实际情况相符,在工程中需优化复合绝缘子几何结构形式,及时排查其使用情况,避免金具破坏影响输电线路的安全运行。

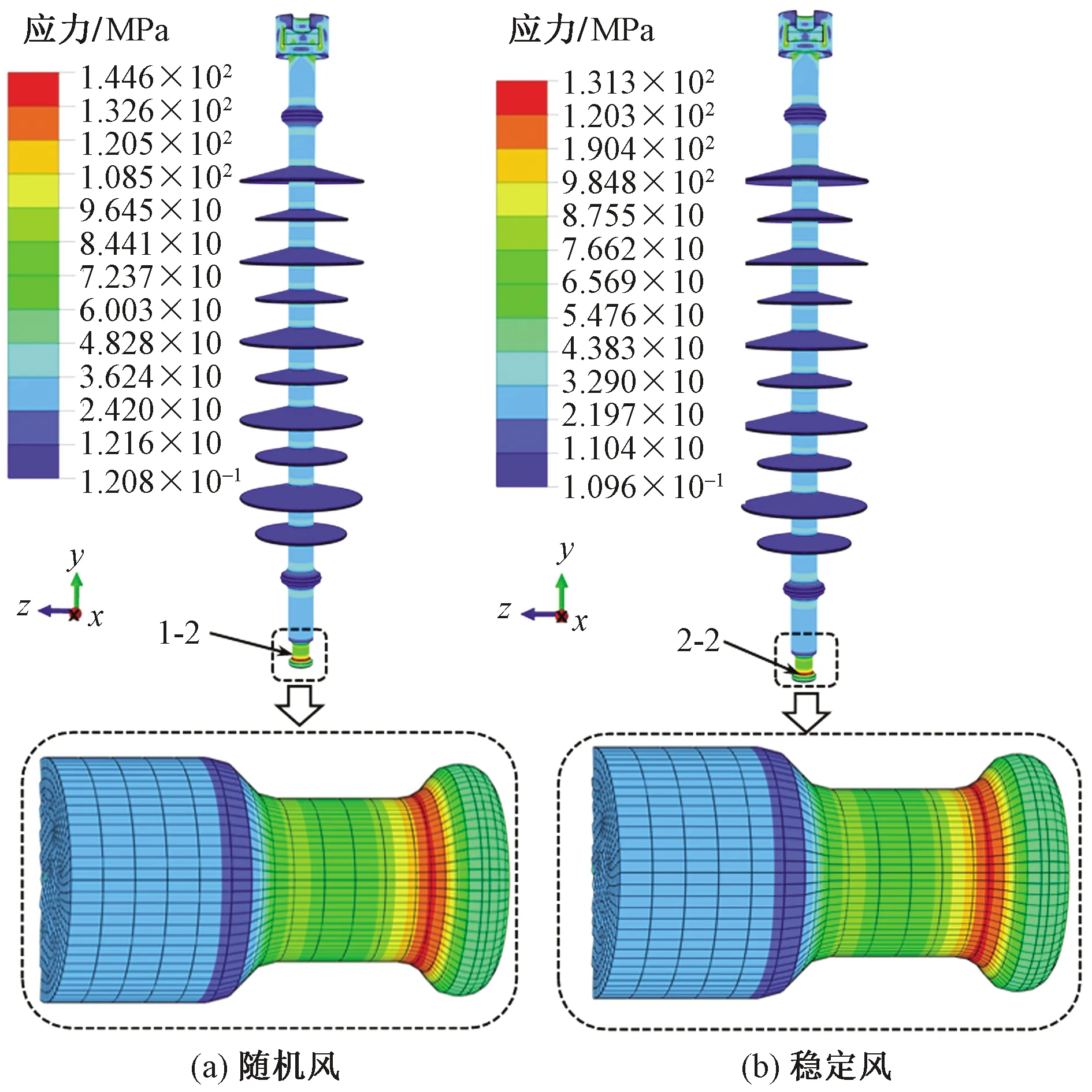
图15 复合绝缘子应力分布情况Fig.15 Stress distribution of composite insulator

图16 复合绝缘子断裂情况Fig.16 Fracture of composite insulator

直角挂板在两种荷载工况下的应力分布差异不大,最大应力仅相差0.1 MPa,但从整体应力分布情况来看,工况1中直角挂板应力集中区域较工况2范围更大,图17中应力主要出现在下端接触区域,且沿x轴正方向区域应力集中较为明显,因此,在直角挂板下端位置相对运动前方区域因为风荷载反复作用,极易发生疲劳失效断裂。同一个模型中,左右两侧直角挂板应力情况相同。

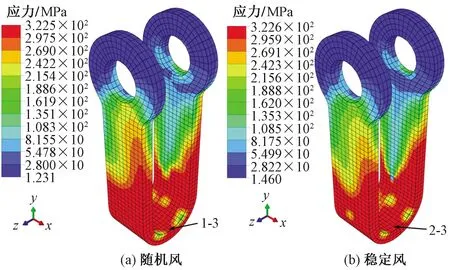
图17 直角挂板应力分布情况Fig.17 Stress distribution of right angle hanging ring

如图18所示,针对碗头挂环,其应力主要集中在球头球窝连接处,两种荷载工况下差异不明显,从应力分布情况来看,碗头挂环具有较好的几何结构优势,相比球头挂环和直角挂板整体应力偏小,可见,当连接金具几何模型的实际结构相对较薄弱时,在外部荷载作用下,整体结构中这些薄弱处极易出现应力集中现象,从而产生明显的应变,即在此处极易发生断裂破坏。

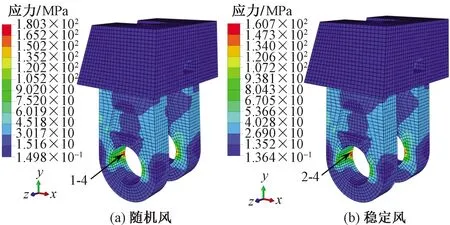
图18 碗头挂环应力分布情况Fig.18 Stress distribution of bowl hanging ring

两种工况下,线夹最大应力均为352.4 MPa,从线夹应力分布情况来看,两种工况下差别不大,单个线夹两个挂环处由于开孔原因,且与螺栓相互作用而产生应变,均为应力集中区域,同一个模型中,左右两侧线夹应力情况相同,图19所示为线夹应力分布情况。

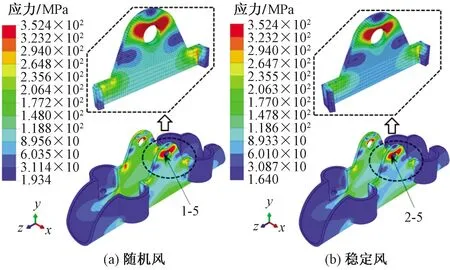
图19 线夹应力分布情况Fig.19 Stress distribution of cable clamp

3.3 连接金具最大应力对比

从局部金具应力分布情况可见,应力集中区域主要出现在:①球头挂环圆环与杆部过渡处；②复合绝缘子底端杆部过渡拐角处；③左右两直角挂板底端接触位置；④碗头挂环与螺栓连接处；⑤左右两个线夹与螺栓连接处。针对这些应力集中区域在5个连接金具上分别选取具有代表性的结点应力,其位置编号情况如表3所示,对比不同区域在两种荷载工况下的应力变化情况。

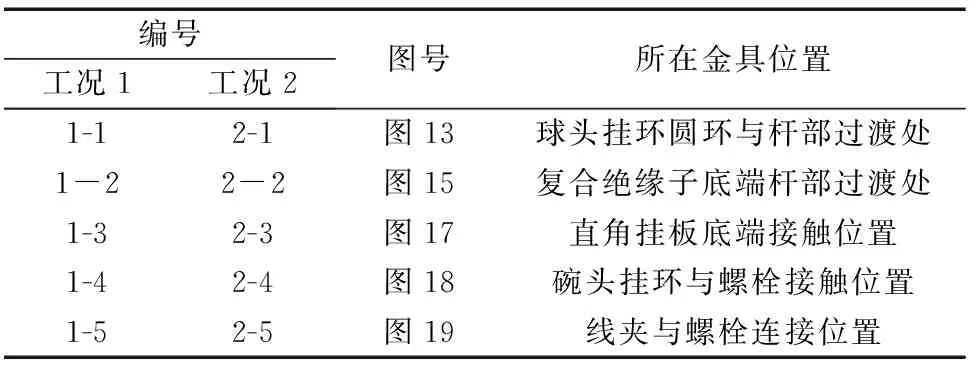
表3 选取结点位置编号Table 3 Number and location of select node

图20中,两种典型荷载作用下,金具自重对金具应力几乎没有影响,可以忽略。当导线重力荷载作用于金具时,其应力迅速增大,但没有达到金具材料本身的屈服强度。当施加风荷载作用时,金具应力逐渐增大,球头挂环、悬垂线夹和直角挂板应力增加比较明显,球头挂环和线夹最大应力已经超过了其材料本身的屈服强度,可见风荷载对于金具的应力有显著的影响,有必要针对风荷载对于输电线路连接金具的影响做深入研究。

对比两种荷载工况,基于稳定风荷载计算方法与基于随机风荷载计算方法模拟的整体金具应力变化情况差异不是很大,表明稳定风荷载计算方法可行。但是针对局部金具而言,如球头挂环,在动态风作用下应力较大,说明动态风荷载对于连接金具的应力有显著影响。通过分析表明,在整体结构中,最容易发生失效断裂的金具为球头挂环,其次是线夹与直角挂板。

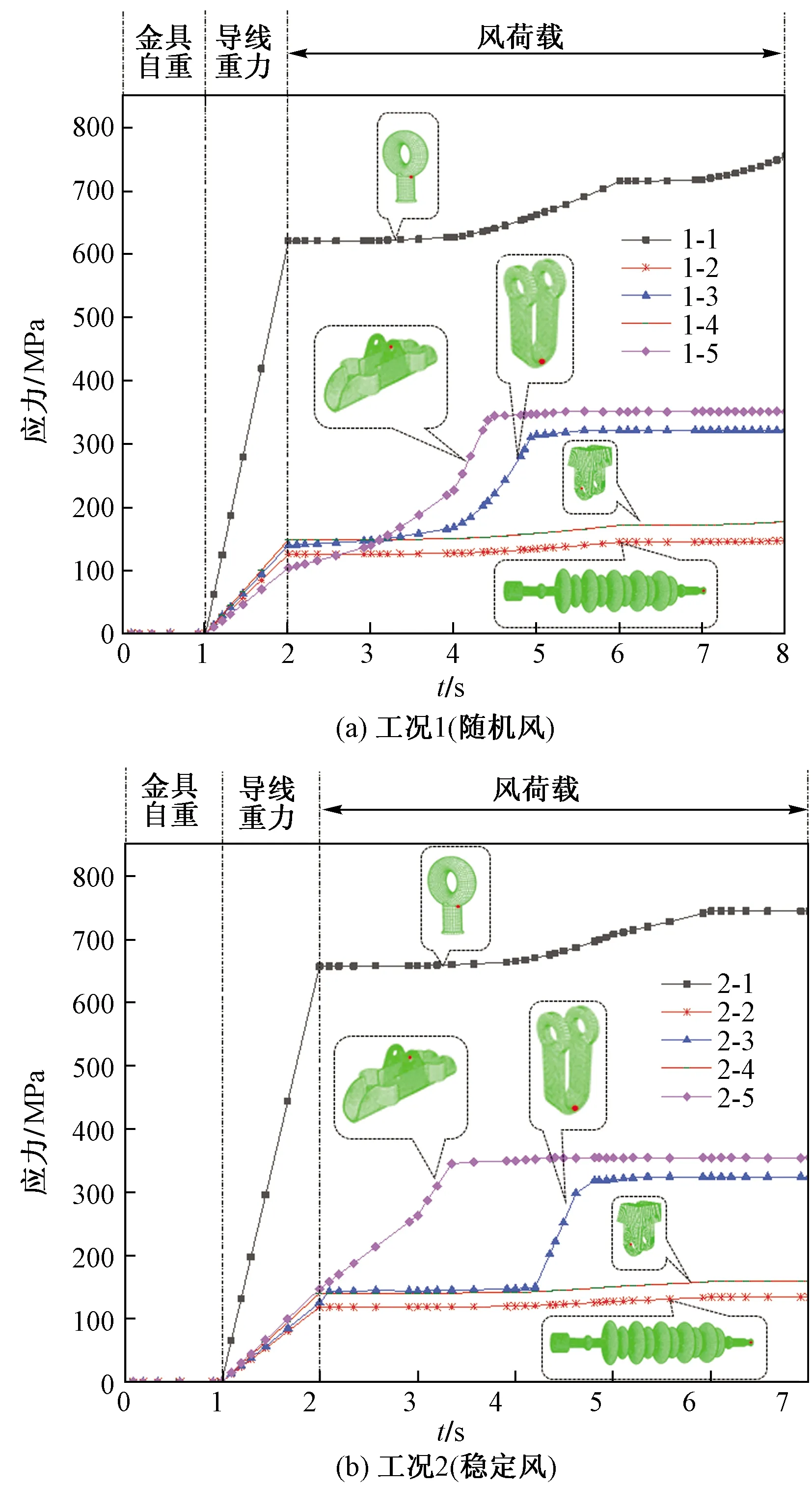
图20 金具局部应力对比情况Fig.20 Local stress comparison of fittings

4 结论

(1)根据金具应力分布情况可知风荷载对于金具的应力有着显著的影响,且随机风对于金具的影响更为突出。

(2)在整体连接金具结构中,球头挂环圆环与杆部连接处由于几何结构形式发生改变,造成局部应力集中,最容易发生失效断裂；其次容易发生破坏的为线夹与螺栓连接位置、直角挂板下端接触位置；复合绝缘子杆部过渡处采用球头球窝连接形式,容易产生弯曲应力,在应力集中区域产生明显的应变,容易在杆部过渡处发生断裂。

(3)建议针对易损金具,可通过提高金具的极限应力、优化几何结构等方法来避免金具的破坏。此外,对于关键部位还应进行定期检查,以避免影响输电线路的安全运行。