智轨电车动力学性能研究

钟汉文，李晓光，肖 磊，杨 勇，张陈林，黄瑞鹏，袁希文

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

智轨电车是一种轨道交通与地面交通融合创新的新型路面交通工具，其依靠胶轮在地面上循迹行驶，可以灵活编组。当前投入商业运行的智轨电车拥有 “两动一拖”三编组结构，最大载客超过300人，各节编组之间采用铰接装置实现编组车辆之间的连接。智轨电车具备公交系统驾驶灵活、低建设和运维成本的优点[1-2]，其结构复杂，车辆架构与双铰接车辆的相近，整车长度远超过普通汽车的，因此行驶过程中整车的动力学表现是影响车辆稳定性和安全性的关键因素之一，也是研究的重点。

针对双铰接结构车辆动力学问题，国内外都开展了相关的研究。徐晓美等提出了一种挂车车轮主动转向控制方法，其根据实际路径与目标路径的预瞄偏差控制量，通过调整挂车车轮转角以减少偏差量，从而提高车辆行驶的稳定性，减少了轮胎磨损[3]。R Craft通过交通数据分析，研究了汽车列车的行驶稳定性并开展稳定性控制研究[4]；Hsun-Hsuan Huang等研究了二次型防侧倾控制算法对重型铰接车辆动力学性能的影响[5]；Sogol Kharrazia等研究了主动转向系统调节转向角对整车稳定性能的影响[6]；李源孰通过对铰接车辆制动力分配的研究，提出了保证运输安全、提高制动稳定性的措施[7]；侯建章研究了双挂车辆制动工况的轴抱死和车间制动力协同计算方法对车辆动力学性能影响[8]。这些研究将双铰接车辆简化为少自由度的数学模型，从设计角度和理论层面对双铰接车辆的动力学性能开展分析研究，对多铰接车辆的研发应用具有理论指导意义。本文基于车辆动力学理论，对3编组智轨电车从2个方面开展车辆动力学建模仿真研究：通过搭建数学模型，开展控制系统的仿真研究，为中央虚拟轨迹线循迹控制器、自动跟随转向控制器的设计和优化提供数据支持；通过搭建整车精细化模型，开展控制系统仿真研究，为整车动力学性能评价与改进提供指导。

1 数学模型及仿真

智轨电车通过中央虚拟轨迹线循迹控制器和自动跟随转向控制器，来实现整车的转向控制。其中，中央虚拟轨迹线循迹控制器主要实现第一节车的转向控制，使得第一节车沿着虚拟轨迹线行驶；自动跟随转向控制器则控制后面两节车的转向，实现与第一节车的轨迹跟随。为了实现控制器的设计和优化，搭建了整车准确数学模型，以快速、便捷地实现转向控制器算法验证。

1.1 数学模型

基于车辆动力学的单车理论搭建整车数学模型（图1）。对于3编组智轨电车，第一节车表示为Mc1，第二节车为Tp，第三节车为Mc2；Mc代表带有司机室的动力车，Tp代表带有充电弓的非动力车。图1中，O1,O2,O3分别为Mc1,Tp, Mc2的车辆质心；Fxi,k为第k车坐标系上第i轴轮胎的纵向力(i=1,2;k=Mc1, Tp, Mc2), N；Fyi,k为第k车坐标系上第i轴轮胎的侧向力，N；Fpj,x,k为第j个铰接点k车所受纵向力（j=1,2），N；Fpj,y,k为第j个铰接点k车所受侧向力，N；δi,k为第k车第i轴转向角度，rad；φj为第j个铰接盘的转向角度，rad。

图1 智轨电车数学模型示意图Fig.1 Schematic diagram of the mathematical model for autonomous-rail rapid tram

对3节编组智轨电车进行车辆受力分解，推导出Mc1的运动学数学方程：

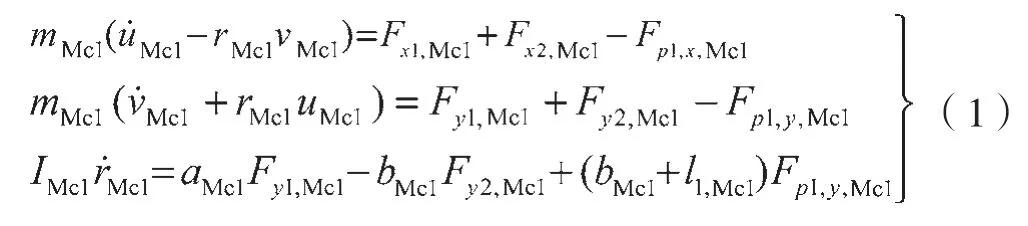
式中：mMc1——Mc1整车质量，kg；IMc1——Mc1转动惯量，kg·m2；rMc1——Mc1 横摆角度，rad；uMc1——Mc1纵向速度，m/s；vMc1——Mc1的侧向速度，m/s；aMc1——Mc1车辆质心到前轴的距离，m；bMc1——Mc1车辆质心到后轴的距离，m；lj,Mc1——第j个铰接点距离Mc1最近轴的距离，m。

同理，可以得到Tp和Mc2的数学方程：

式中：mTp——Tp整车质量，kg；ITp——Tp转动惯量，kg·m2；rTp——Tp 横摆角度，rad；uTp——Tp 纵向速度，m/s；vTp——Tp侧向速度，m/s；aTp——Tp车辆质心到前轴的距离，m；bTp——Tp车辆质心到后轴的距离，m；lj,Tp——第j个铰接点距离Tp最近轴的距离， m。

式中：mMc2——Mc2整车质量，kg；IMc2——Mc2转动惯量，kg·m2；rMc2——Mc2横摆角度，rad；uMc2——Mc2纵向速度，m/s；vMc2——Mc2侧向速度，m/s；aMc2——Mc2车辆质心到前轴的距离，m；bMc2——Mc2车辆质心到后轴的距离，m；lj,Mc2——第j个铰接点距离Mc2最近轴的距离，m。

对铰接点进行受力分解，推导出2个铰接点的受力关系：

1.2 仿真验证

利用所推导的数学方程在Simulink中搭建模型，开展R25稳态圆周工况仿真，得到各轴转向角与铰接盘转向角数据，具体如图2和图3所示。通过后续的样车测试，也得到各轴转向角和铰接盘转向角的数据，如图4和图5所示。通过仿真与测试的数据对比可知，各轴转向角和铰接盘转向角在变化趋势上一致性较好，表明搭建的数学模型在一定程度上能反映车辆的真实状态。利用数学模型搭建的仿真模型能快速便捷地实现转向控制器算法的仿真验证，为控制器的开发、调试及验证提供数据支撑。

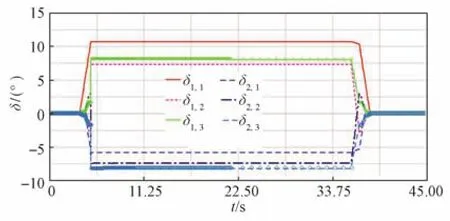
图2 智轨电车数学模型稳态圆周工况各轴转向角Fig.2 Axles steering angle of mathematical model in constant radius cornering case for autonomous-rail rapid tram

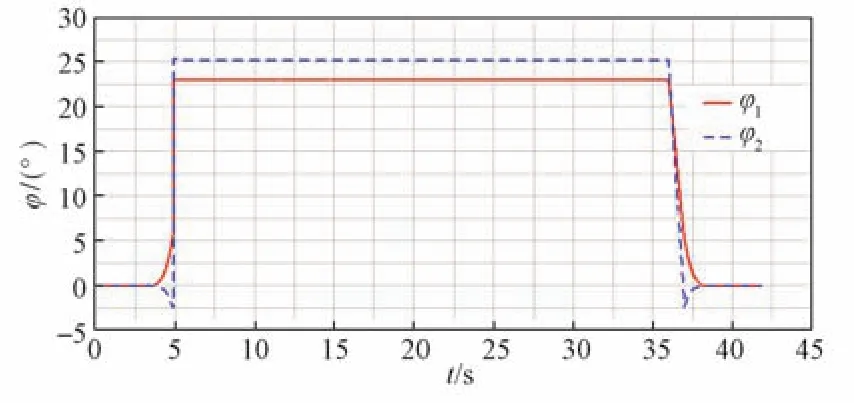
图3 智轨电车数学模型稳态圆周工况铰接盘转向角Fig.3 Articulation angle of mathematical model in constant radius cornering case for autonomous-rail rapid tram

图4 智轨电车稳态圆周工况各轴转向角测试值Fig.4 Axles steering angle of real vehicle test in constant radius cornering case for autonomous-rail rapid tram

图5 智轨电车稳态圆周工况铰接盘转向角测试值Fig.5 Articulation angle of real vehicle test in constant radius cornering case for autonomous-rail rapid tram

2 虚拟样机模型及仿真

车辆虚拟样机模型是研究车辆特性的基础，建立能准确反映车辆动力学特征的模型是智轨电车动力学性能研究的重点。整车虚拟样机模型其实质是利用车辆的数学模型来描述外界对车辆的输入、车辆系统以及车辆系统对外界的输出三者之间的关系。该模型既要保证对运动系统描述的准确性，又要将对研究目标影响不大的因素进行简化，以提高运算速度。

2.1 模型搭建

为了保证模型的准确性，考虑到车辆受相对运动部件的影响，采用Simpack软件搭建虚拟样机模型。梳理整车各系统间的拓扑关系，具体如图6所示。根据拓扑关系，整理三维设计模型、装配图纸及弹性参数测试报告，获取相应的质量惯量、布置位置及弹簧阻尼等参数，从而建立智轨电车的车辆动力学模型（图7）。该模型共涉及159个相对运动部件及440个自由度。

图6 智轨电车车辆拓扑关系Fig.6 Vehicle topological relationship of autonomous-rail rapid tram

图7 智轨电车车辆动力学模型Fig.7 Vehicle dynamic model of autonomous-rail rapid tram

2.2 模型验证

为了验证所建立的部件级动力学模型在弯道工况下的精准性，设计了一个直角转弯工况进行模型验证。选择一个直角转弯路线，采集车辆在直线行驶—转弯行驶—直线行驶整个过程中的速度信号、第一轴转向角信号及前后两个铰接盘转向角信号。其中，速度和第一轴角度作为动力学模型验证的输入，通过Matlab和Simpack的联合仿真，实现试验工况运行；2个铰接盘转向角作为仿真测试的对标指标，来验证模型的准确性。试验过程中，以Mc1为驾驶端，相应的采集数据也按Mc1为第一车排序。

图8和图9为铰接盘的仿真和测试数据对比。由图可见，在仿真和试验过程中，车辆的铰接盘转向角在变化趋势和变化幅值方面都非常吻合。由此可知，所建立的智轨电车部件级动力学模型能够较真实地反映车辆的运动学特征。

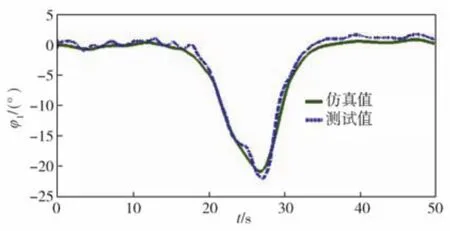
图8 铰接盘1转向角度的仿真与测试曲线Fig.8 Simulation and test results of articulation 1 angle

图9 铰接盘2转向角度的仿真与测试曲线Fig.9 Simulation and test results of articulation 2 angle

2.3 工况设定

智轨电车整车长度约为32 m，其在弯道行驶的动力学性能会直接影响整车的行驶稳定性和安全性。因此，依据ISO 14791-2000标准要求[9]，对智轨电车进行从稳态直线到稳态圆周的行驶工况设计，不仅考虑了稳态工况下车辆的动力学性能，同时也考虑了由稳态到瞬态变化过程中的动力学性能变化。考虑到车辆的侧向加速度小于0.4gn（gn=9.806 65 m/s2），车辆动力学响应还处于线性阶段，为了更好地展示智轨电车动力学性能，设定其以8 m/s的速度直线稳定行驶50 m，通过第一轴转向控制进入半径为30 m的圆周，转向稳定后保持稳态圆周运动，其运行轨迹设计如图10所示。

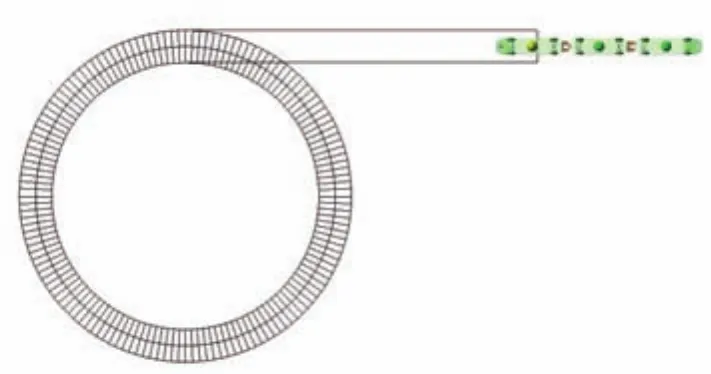
图10 稳态圆周工况轨迹Fig.10 Path of constant radius cornering case

在稳态圆周运动过程中，车辆质心侧偏角变化非常小，设定车辆的瞬时转动半径与道路曲率保持一致，以便于对车辆动态响应的研究。

不考虑车辆的侧偏，定半径R转弯工况下，第一轴目标转向角δR与轴距L的关系如下：

对于第一轴转向角控制，采用PID控制方法，PID控制输出量表达式如下：

式中：u(t)——PID控制输出量；Kp，Ti，Td——PID的控制参数；δ(t)——上一个时间步长第一轴的转角测量值。

实际仿真过程中，设定稳态圆周的转弯半径为30 m，通过调整PID控制参数，实现车辆在稳态圆周工况下运行。

2.4 稳态行驶控制

基于第一轴转向角控制算法，结合自动循迹转向控制算法，通过Matlab编程得到转向控制程序。在程序中，输入信号为转弯半径以及车辆动力学模型的速度、位移、角度等信号，输出为车辆动力学模型中的各轴转向角，通过Matlab和Simpack的联合仿真，研究各节车辆的横摆角速度和侧向加速度变化，评价在该工况下智轨电车的动力学性能。

图11和图12为智轨电车在稳态圆周工况下的各节车辆的横摆角速度、侧向加速度变化曲线。由图可以看出，从直线稳态到圆周稳态过程中，2个指标的变化趋势比较一致，均为Mc1车数值变化最大、Tp次之、Mc2最小。

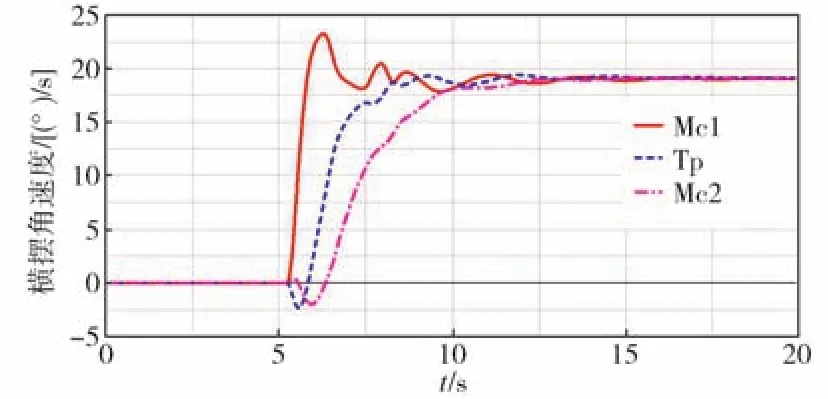
图11 智轨电车各节车辆横摆角速度Fig.11 Yaw rate of each section for autonomous-rail rapid tram

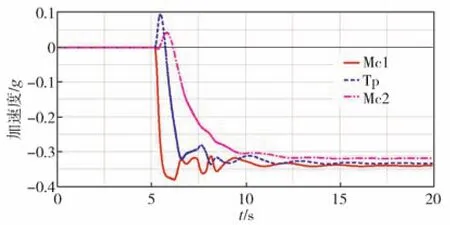
图12 智轨电车各节车辆侧向加速度Fig.12 Lateral acceleration of each section for autonomous-rail rapid tram

在铰接车辆中，后部放大系数是一种侧向加速度放大率的量化指标，利用首末节车质心处的侧向加速度的比值来研究铰接车辆的侧向动力学特征（该数值通常大于1）[10]，其表达式如下：

式中：ayk——车辆运行过程中，第k节车侧向加速度；A——后部放大系数。

通过仿真数据曲线，可以得到智轨电车在稳态圆周工况下A=0.94；仿真曲线没有呈现侧向加速度放大的趋势，表明智轨电车的动力学性能要优于传统铰接车辆的。

3 结语

针对胶轮承载、多编组、虚拟轨道运行的智轨电车，本文开展整车动力学性能研究。首先搭建了智轨电车整车数学模型，仿真测试结果表明，所建立的数学模型在动力学性能变化趋势上仿真值和实测数据吻合度较好；然后通过搭建细化的Simpack整车模型，开展了工况研究，利用后部放大系数进行动力学性能评价，结果显示智轨电车的动力学性能要优于传统铰接车辆的。文中所提方法不仅为后续整车性能的优化提供评判依据，也可为智轨电车后续的牵引、制动、转向协同控制算法的研究提供准确的仿真数据。