边坡偏压对于邻近地铁车站基坑稳定性影响分析

李 浩, 刘 毅, 彭 振, 唐晓杰, 李元海

(1.中交(广州)建设有限公司，广东 广州 511458；2.中交第二航务工程局有限公司 技术中心，湖北 武汉 430040；3.中国矿业大学 力学与土木工程学院，江苏 徐州 221116；4.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116)

为缓解随城市化推进所带来的日益增长的交通压力，我国的地铁建设近年来得到了大力发展.在地铁修建过程中，其车站多以基坑形式进行施作，而城市基坑工程的设计及施工往往受到各种条件制约，包括邻近的建筑结构和复杂的工程地质条件等[1-3].随着城市地铁网络的扩张，边坡偏压作为一种典型的地质情况变得越发难以避免.与传统基坑不同，偏压基坑的受力模式以及由于开挖所引起的环境效应将发生很大改变[4-6]，这给基坑的设计、支护及施工带来了挑战[7-9].

对于偏压基坑的开挖稳定性问题，当前学者基于数值模拟及现场监测等手段已开展了相关的研究.石钰锋等[10]和LIU J.等[11]针对工程实例，基于现场监测数据分析了基坑围护结构的变形特征，指出偏压环境下的基坑变形控制是保障施工安全的关键要素.雷崇采用有限元软件PLAXIS模拟了大偏压深基坑开挖全过程，并提出在大偏压作用下基坑两侧的支护结构位移、内力与常规基坑存在较大差异，设计中需根据实际受力采用相应的支护及加固措施[12].刘波等针对偏压非等深基坑的开挖效应问题采用有限元进行模拟分析，得出偏压环境下的地表沉降分布具有明显的空间效应[13].上述研究表明，偏压环境对于基坑的影响主要体现在围护结构变形、内力分布以及地表沉降等方面.随着邻近的边坡高度变化，这些涉及基坑稳定性的关键要素由于地应力分布的改变亦会随之受到不同程度影响[14-15].现有研究多基于特定的工程实例进行分析，鲜有涉及边坡偏压条件变化对于基坑稳定性的影响规律，有必要开展进一步的研究.

本文依托深圳市轨道交通2号线莲塘口岸站工程背景，立足偏压基坑的稳定性问题，采用有限差分软件FLAC对不同边坡高度条件下的土体沉降、围护结构变形及应力分布特征进行了模拟分析，并获得其变化规律.本文的分析结果对于偏压基坑的设计及工程安全的控制具有重要的参考意义.

1 工程概况

莲塘口岸站为深圳市城市轨道交通2号线三期工程的第一个车站，车站基坑采用顺逆结合施工方式进行开挖，最大开挖深度达到地下31 m.车站西南角为猫窝山，地形东低西高，坡底高程18.6 m，坡顶高程44.1 m，高差大，坡度陡，对基坑产生偏压作用.基坑开挖前进行削坡支护处理，南侧边坡分二级支护.削坡后坡脚距基坑13.7 m，北侧为一级边坡，距基坑24.4 m.

研究区表层广泛分布素填土及粉质粘土.素填土颜色呈灰黄、褐黄、褐红等杂色，结构一般呈松散～稍密状态，主要由粘性土混少量砂砾组成，局部夹有碎块石.粉质粘土呈灰褐色，可塑状，在研究区内呈透镜体状不连续分布.下伏基岩为强～微风化石英砂岩，强风化岩体呈硬土状，中风化及微风化岩层节理裂隙发育.

2 有限差分数值模拟

2.1 数值模型

采用FLAC二维模型对不同工况下的基坑开挖全过程进行建模分析.研究区地层基本呈层状分布，削坡面范围较大，可采用平面模型进行简化分析.根据工程经验以及数值计算结果，基坑开挖影响宽度约为深度的3～4倍，影响深度约为开挖深度的2～4倍[16].因此，本次数值计算模型的长度定为150 m，最大高度定为93 m.模型的左右边界施加水平方向约束，底部边界施加竖向约束.数值模型以30 902个节点划分15 179个单元.如图1所示，基坑第一级及第二级边坡分别设置4根和5根φ22全长粘结锚杆.同时基坑范围内在地面以下0.5、6、10.5、15.5、20、25m处设置6道水平支撑.第一、三、五道支撑采用钢筋混凝土支撑，尺寸为800 mm×1 000 mm，第二、四、六道支撑采用钢支撑φ800(t=20 mm).基坑模拟开挖分6步进行，分别开挖至地下1.5、7、11.5、16.5、21、26、30 m深度.

2.2 计算参数

计算区内土体采用摩尔-库伦模型，岩土参数(表1)依据现场实验及实验室的测试结果确定.冠梁采用弹性单元体，弹性模量及泊松比分别取30 GPa和0.3.围护桩、全长锚杆及水平支撑采用FLAC内置结构单元pile、cable以及beam进行模拟(表2).

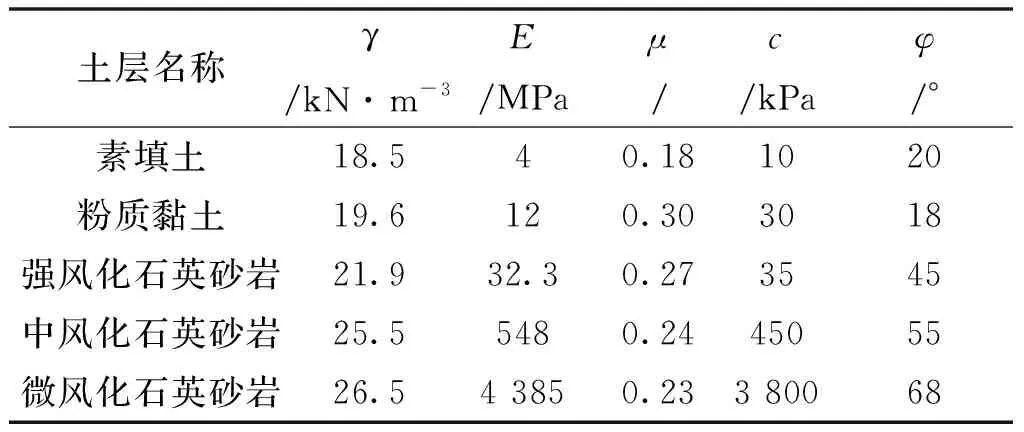
表1 岩土体模型物理力学参数

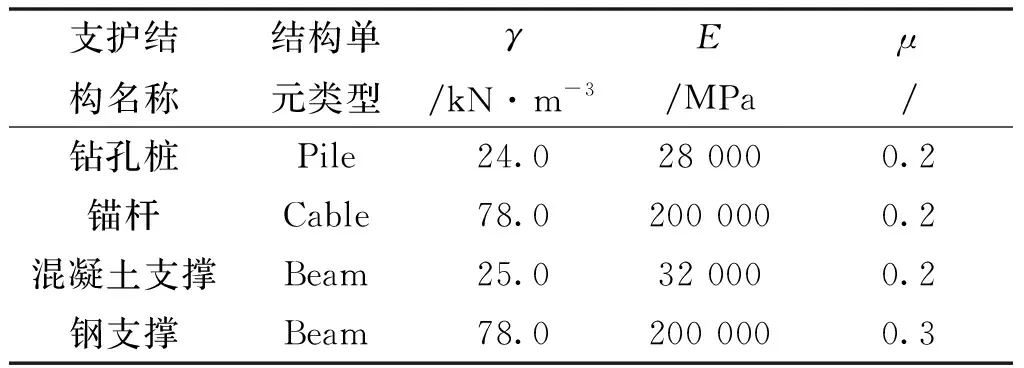
表2 支护结构参数

2.3 计算方案

为分析不同偏压强度对于基坑稳定性的影响，选取不同边坡高度进行基坑开挖稳定性分析.取实际偏压条件作为分析参照，共采用5种计算方案，边坡高度数据如表3所示.不同高程的边坡均采用二级削坡锚固，基坑支护参数一致.本文定义偏压强度为数值模拟的边坡高度与实际高度的比值，共设置5种偏压强度情况进行分析.

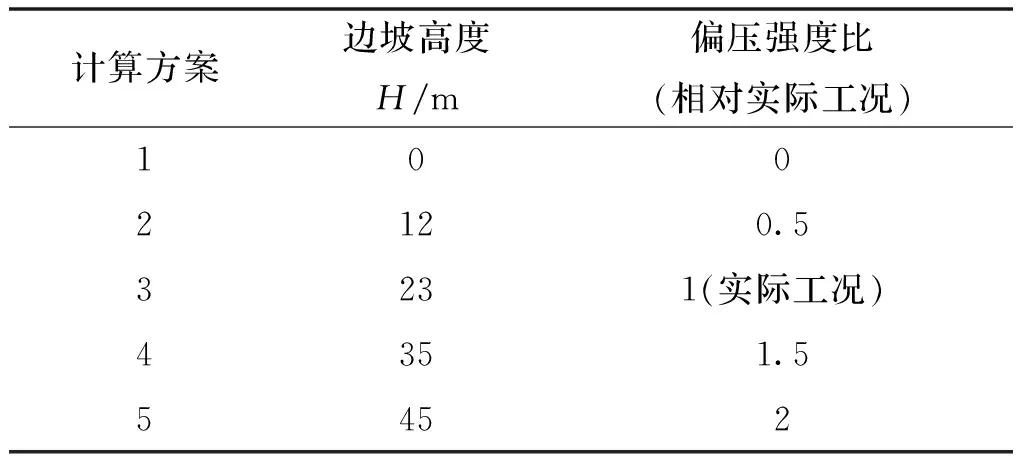
表3 偏压强度分析计算方案

3 计算结果

3.1 监测数据对比分析

取实际偏压环境下的模拟数据与监测值进行对比分析.如图2(a)所示，现场监测值与模拟数据在远坡处的地表沉降变化趋势基本一致，且处于同一数量级内，最大误差小于1 mm，可见模型及其参数设置合理.如图2(b)所示，数值分析所获得的近坡桩水平变形模式与实际监测大致相同，最大水平变形出现在桩体中部，而桩顶水平变形基本相同，监测值为3 mm，模拟值为2 mm，误差较小.从对比结果上看，模拟结果可基本反映工程现场中变形数据的变化规律，下文的分析对实际工程具有指导意义.

3.2 偏压强度对于地表沉降影响

图3为实际工况下(偏压强度=1)基坑开挖完成后的地层沉降云图(图中基坑右侧为远坡，且不显示结构单元)，图中地层隆起为正、沉降为负.由图中可以看出，地层的隆起区主要分布在坑底及基坑围护墙处，并呈现向基坑外侧衰减的趋势.沉降区主要分布在远坡处地表附近，沉降区形状为凹槽式分布，这与相关的研究结果是相符合的[17].地层隆起、沉降分布特性一定程度上也验证了本次分析参数及模型边界选取的合理性.

本次模拟所分析的5种逐渐升高的偏压情况下，开挖影响范围分别为37 m、38 m、39 m、41 m、41 m.可以发现随邻近边坡高度(偏压强度)的增加，沉降区的影响范围逐渐向基坑外侧扩展.此外，随偏压的加大，地层沉降区范围有向深部土体扩展的趋势，5种偏压情况下，沉降区影响深度分别为9 m、10 m、12 m、13 m、14 m.

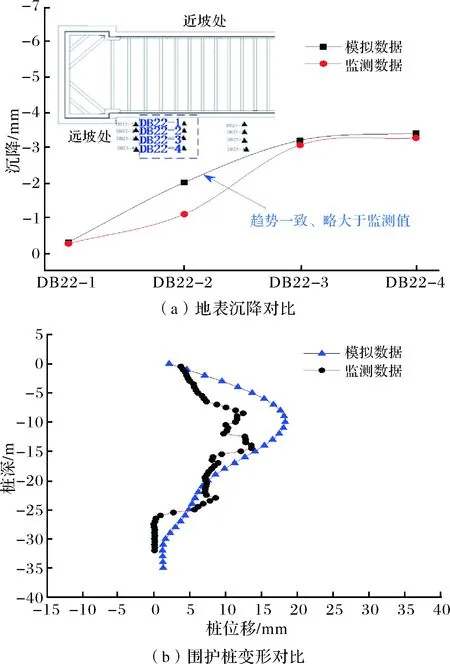
图2 模拟数据—实际监测数据对比Fig.2 Comparison of the monitor and simulated data

图3 原型基坑周围地层沉降云图(单位：米)Fig.3 Nephogram of practical ground subsidence around the foundation (Unit: m)

基坑外侧的沉降分布情况对于周边建筑物的变形控制以及基坑工程的施工安全具有重要意义，为定量识别边坡高度对于基坑外侧地表沉降的影响规律，提取了远坡侧的地表沉降数据进行分析.如图4所示，5种偏压条件下，远坡处地表均呈现为凹槽式沉降：基坑围护墙处出现小范围的隆起，之后向坑外处产生逐渐增大的沉降现象，并在距基坑围护墙一定距离处出现最大沉降点.随后地表沉降值逐渐减小直至影响边界.随偏压强度的增大，地表最大沉降值逐渐增大，出现最大沉降点的位置逐渐向基坑外侧移动，从距基坑围护墙7 m处逐渐扩至11 m处，这与偏压造成的地应力分布变化有关.

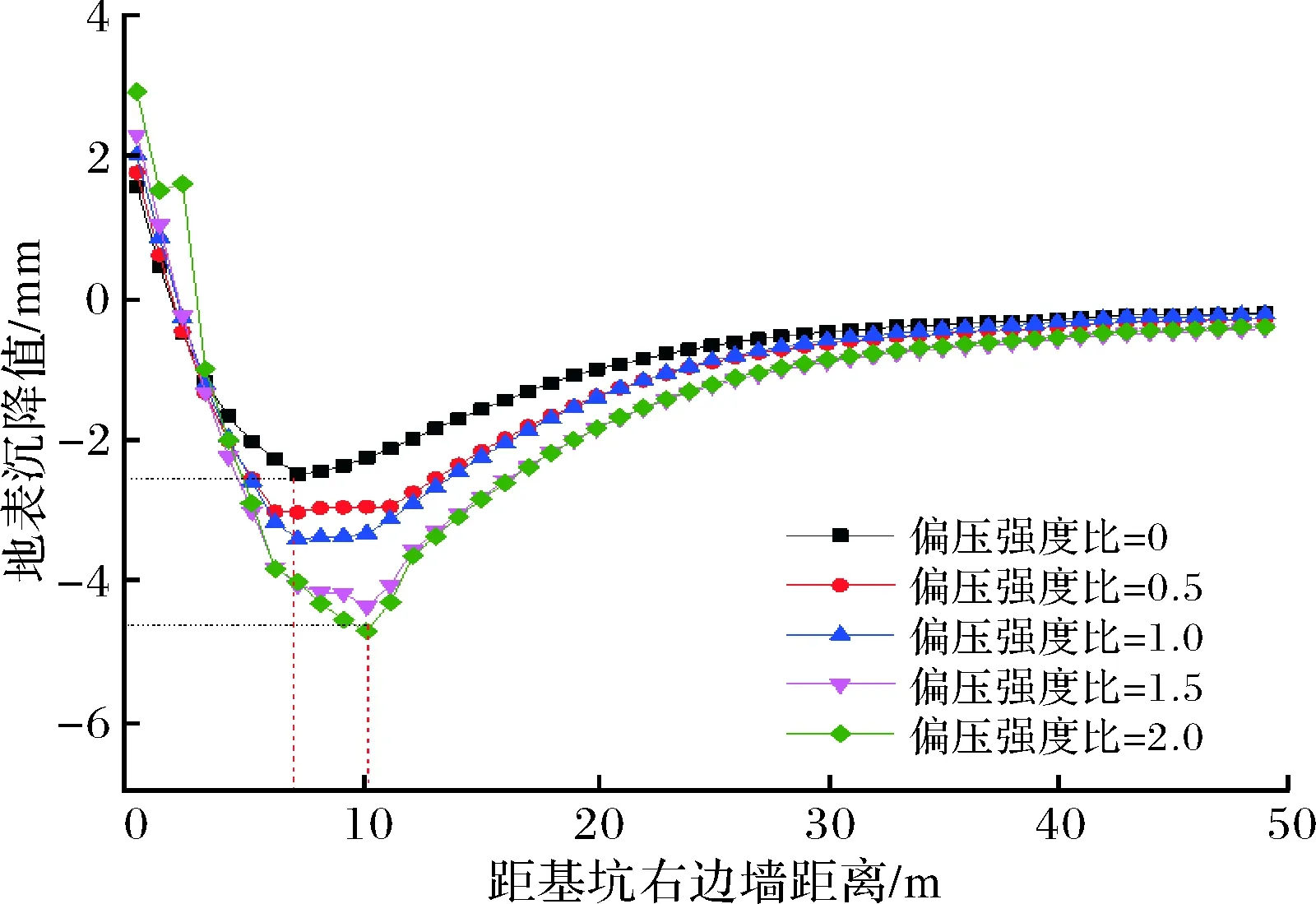
图4 远坡处地表沉降影响范围Fig.4 Surface settlement scope at the area away from the slope

结合图3和图4，边坡高度的变化对于远坡处沉降影响程度较小，但对于地表最大沉降值的影响较为明显.提取各偏压条件下远坡处的地表最大沉降值进行拟合，拟合结果如图5所示.从结果上看，地表最大沉降值随边坡高度的增加呈指数型增长的趋势，最大沉降值与边坡高度的关系式为：y=-1.42+3.13e(x+21.9)/97.9.其中相关系数R2为0.998，说明拟合度较高，可反映地表最大沉降的变化趋势.

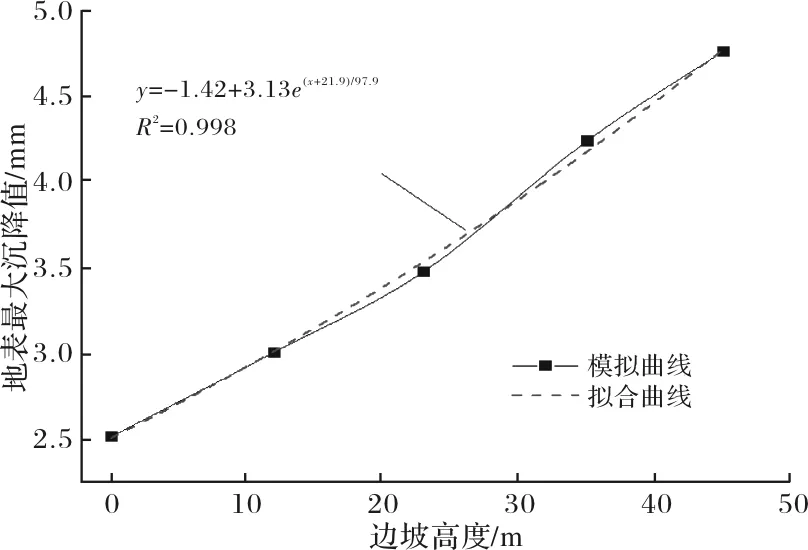
图5 远坡处地表最大沉降值拟合曲线Fig.5 Fit curves of maximum surface settlement at the area away from the slope

3.3 偏压强度对于围护桩变形影响

围护桩作为控制基坑土体变形、保障基坑工程安全的关键结构，其变形行为对于基坑稳定性的控制具有重要意义[18].图6为5种逐渐升高的偏压环境下基坑近坡桩及远坡桩的变形曲线.从图中可以看出：不同偏压环境下，近坡桩和远坡桩的变形模式基本相同，呈现一种类“弓形变形”，最大水平变形出现在桩体中部，桩顶及桩底处变形值较小.此种“弓形变形”特征反应出基坑中部围护结构更易于发生水平变形.

随着偏压的增大，近坡桩及远坡桩的“弓形变形”特征逐渐向“前倾型”转变，桩顶变形逐渐增大.不同偏压环境下，近坡桩及远坡的桩底的变形值基本不变，但桩顶及桩体中部产生了较大幅度的变形增量.这种现象在近坡处体现得尤为明显.图中可以看到，5种逐渐升高的偏压环境下，近坡桩的桩顶变形从-9 mm增加至15 mm，桩体中部的最大变形量从6 mm增至37 mm.而远坡桩受边坡偏压的影响，原本向坑内的变形量逐渐减小，并向坑外产生了小幅的变形.

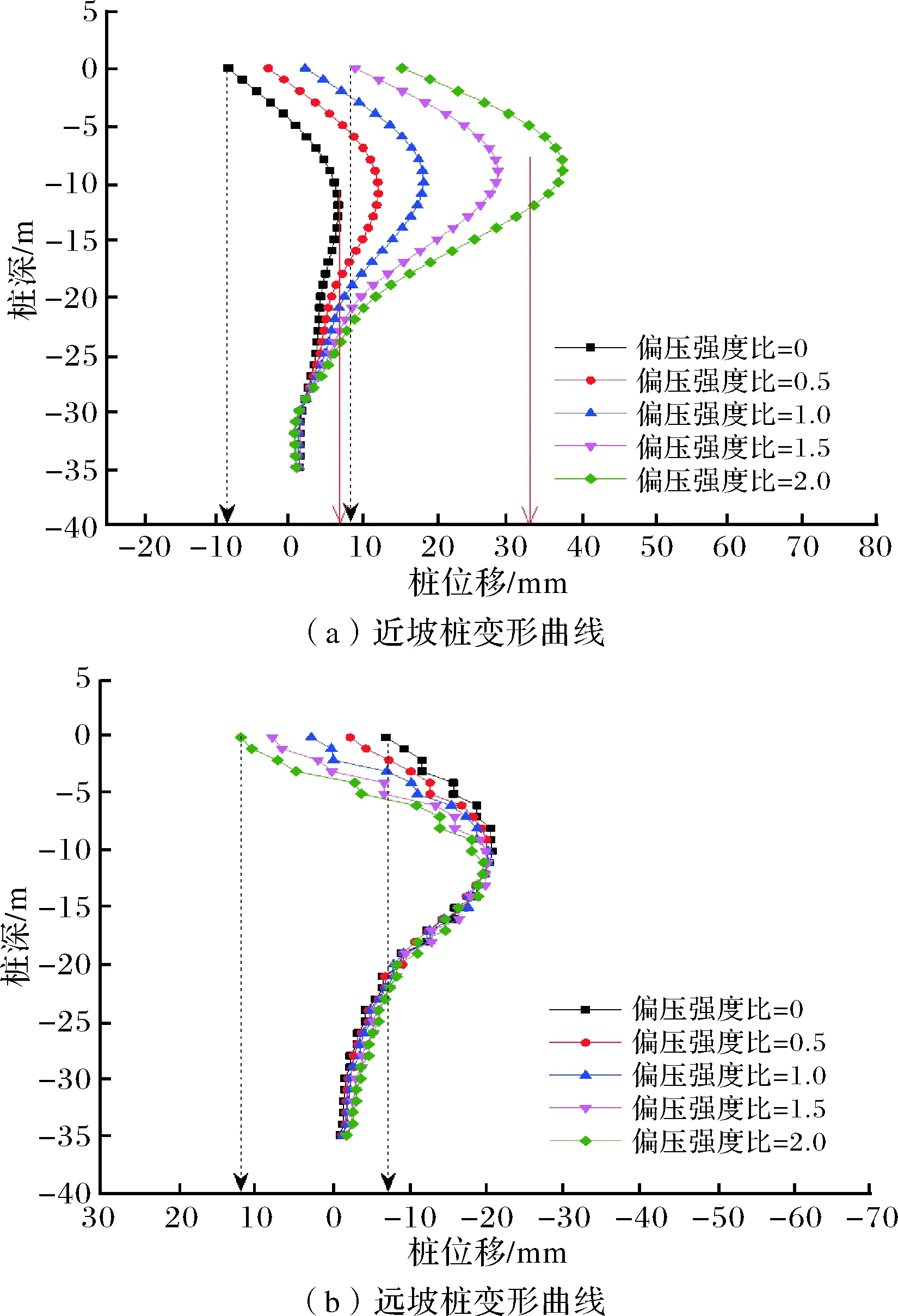
图6 不同偏压强度下围护桩深与桩变形关系曲线Fig.6 Relation curves between pile deformation and buried depth under different bias conditions

由图6(a)可知，偏压变化对于远坡桩的最大水平变形影响不大，而对于近坡桩影响较为明显.为定量获取其最大水平变形与边坡高度之间的关系，选取变形数据进行拟合，如图7所示.从图中可以看出，随边坡高度的增加，近坡桩最大水平变形值呈指数型增长，两者拟合关系为：y=-13.29+20.8e(x-2.7)/47.6，相关系数R2为0.996，拟合度较高.

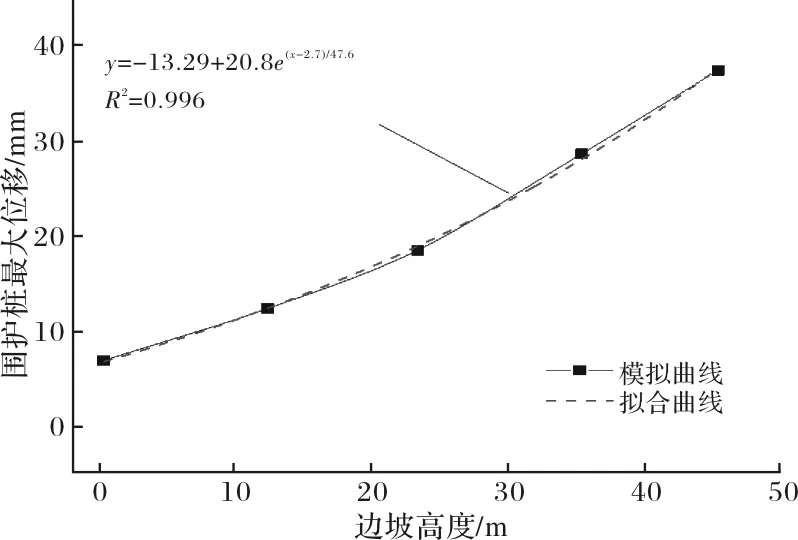
图7 不同偏压强度下近坡桩最大水平变形拟合曲线Fig.7 Fit curves of maximum horizontal deformation of near-slope pile under different bias conditions

为分析边坡高度与近坡桩及远坡桩桩顶变形的关系，对两者数据进行公式拟合，拟合曲线如图8所示.近坡桩桩顶变形服从关系式：y=-42.89+37.8e(x-8.1)/86.2，远坡桩服从关系式：y=-145.74+64.7e(x+273.1)/356.7.两者的相关系数R2分别为0.999和0.996，拟合度较高，可反映桩顶变形与边坡高度的关系.

基坑围护墙处的剪应力分布情况反映了围护桩及基坑土体中易于破坏的风险区域.图9为5种偏压环境下基坑围护墙处的剪应力分布云图(基坑左侧为近坡).从图中可以看出，基坑围护墙处的最大剪应力主要分布于基坑坑底，且近坡处的受剪情况要明显高于远坡处.由此可见，在围护桩设计参数选取过程中，近坡处及坑底处需重点关注.此外，随着偏压强度的增大，围护墙处的最大剪应力也相应增加.5种偏压条件下，最大剪应力从1.5 MPa增至4.6 MPa.桩-土系统中，两者的相对位移会在桩和土体中产生剪切应力[19]，上述剪应力分布现象一定程度上表明在基坑底部更易于产生桩-土相对位移，此种情况在实际工程设计与施工中需给予重点监测，而在实际工程中为避免产生较大位移可基于现场状况采用注浆法进行重点区域加固.

进一步拟合基坑围护墙处土体的最大剪应力值与边坡高度之间的关系，得到如下关系式：y=-465+193.5×e(x+5 972)/6 785.相关系数R2为0.999，拟合度较高，可反映最大剪应力随边坡高度的变化情况.

3.4 不同偏压强度下基坑侧向土压分析

基坑围护桩后土压力的大小和分布对支护结构体系的内力、变形和稳定性验算有着决定性的作用[8].土压力的大小直接影响基坑及围护桩的变形情况.绘制不同边坡高度环境下基坑围护墙处的土压力分布曲线，如11图所示.近坡及远坡处基坑围护墙侧的土压力均表现为随深度的增加而增大.另外，随边坡高度的增加，各深度处的侧向土压力值均相应增大，这种现象在近坡处更为明显.可以发现，近坡处基坑底部土压力的增长趋势更为明显，且随边坡高度的增加，坑底处更容易发生剪切破坏现象.

图8 不同偏压强度下围护桩顶变形拟合曲线Fig.8 Fit curves of pile-top deformation under different bias conditions

图9 基坑围护墙土层最大剪应力分布云图(单位： Pa)Fig.9 Nephogram of max shear stress within the ground near the retaining wall (Unit: Pa)

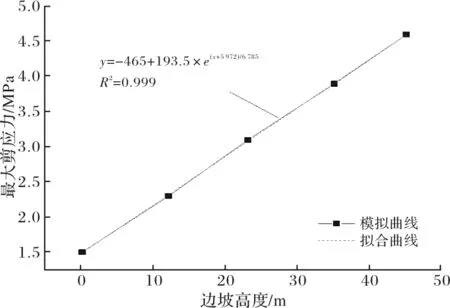
图10 土层最大剪应力与边坡高度关系曲线Fig.10 Relation curves between max shear stress and slope height

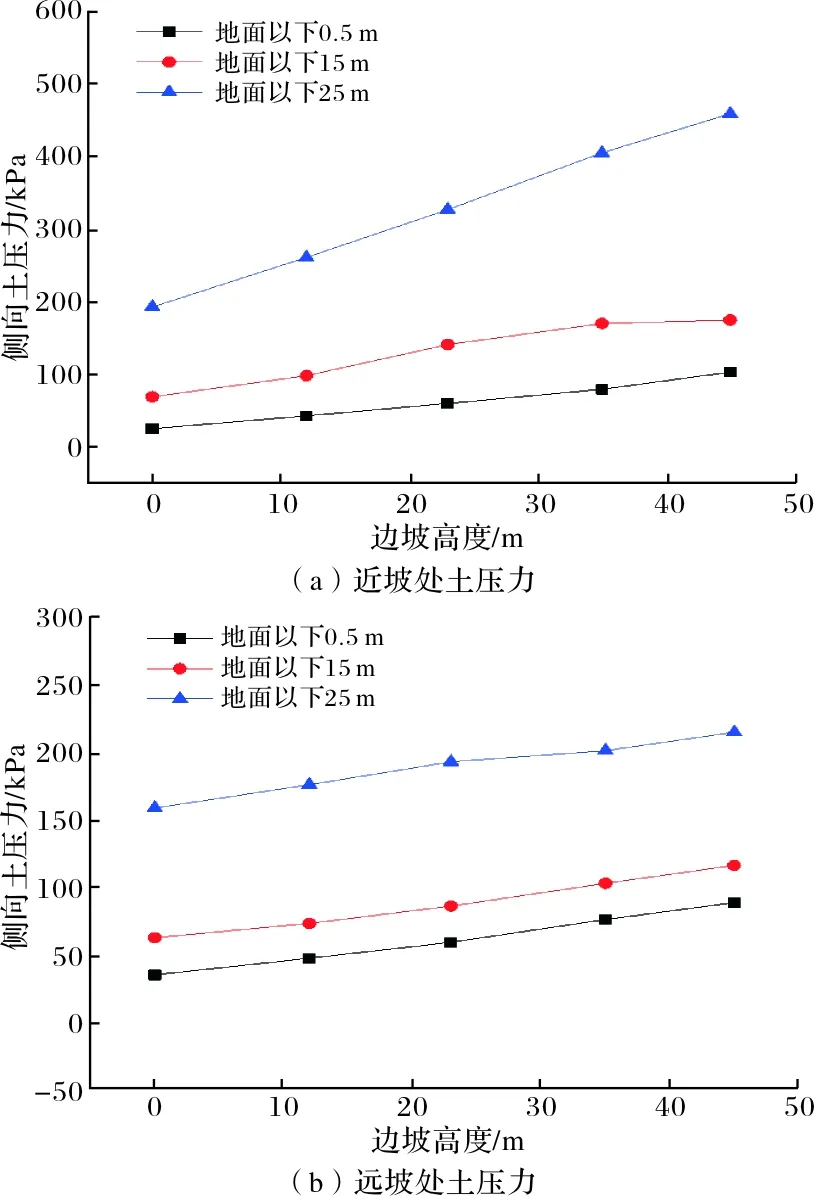
图11 不同偏压强度下基坑周围土压力分布曲线Fig.11 Soil pressure distribution curve around the foundation pit under different bias conditions

4 结论

本文通过建立数值计算模型分析了5种偏压情况下基坑地表沉降、围护桩变形及剪应力的变化规律，得到以下结论：

(1)地表沉降范围及最大沉降值均随边坡高度的增加而增大.边坡高度对于远坡处地表最大沉降值的影响较为明显，最大沉降值与边坡高度的拟合关系为：y=-1.42+3.13e(x+21.9)/97.9.

(2)近坡桩桩顶及桩体中部受偏压影响较大，远坡桩在桩顶处出现明显的变形增量.随边坡高度增加，围护桩最大水平变形呈指数型增长.

(3)随边坡高度的增加，基坑围护墙处的最大剪应力分布于基坑底部，表明此处易于发生剪切破坏.在实际工程中需重点关注此种现象，加强此位置的监测防控.

(4)随边坡高度的增加，近坡及远坡处基坑围护墙处的侧向土压均相应增大，增长趋势在近坡处更为明显.