转发式低轨单星多普勒定位解算技术

易卿武

(1.卫星导航系统与装备技术国家重点实验室，石家庄 050081;2.西安电子科技大学 电子工程学院，西安 710071)

0 引言

卫星导航系统受其信号电平低和高纬地域覆盖不足等因素影响，存在精确性、可靠性、可用性和抗干扰性等方面的不足。为保障复杂环境下持续可靠的导航定位能力，完善军用PNT体系，除提高卫星导航系统及接收机的抗干扰和自主化能力外，国外开展了无线电备份导航定位技术的研究，包括伪卫星定位技术[1-3]、e-Loran技术[4-5]等。小型低轨卫星具有快速部署、抗摧毁等优势，作为一种备份导航技术，单星定位可通过更少的卫星实现目标区域的短期快速定位，解决需要定位信息但对精度要求不高的场景，利于卫星快速部署，且可采用通信卫星等非导航任务卫星实现。近年来基于低轨卫星的备份导航定位技术得到了一定研究，主要集中在采用少量卫星实现定位的算法和性能分析，包括基于伪距和测高的双星或三星定位[6]、基于星上测向的单星定位[7-9]、基于信号多普勒变化率的单星定位[10-12]、信号抗干扰能力[13]分析等。在文献[14]提出了一种基于伪距和多普勒定位的定位方法并对低轨卫星信号覆盖能力进行了分析，相似定位方式在搜寻客机中得到实践[15]。本文针对于低轨卫星的应用特点，对伪距多普勒联合定位原理、迭代算法及定位分布特征进行分析探讨，并基于软件仿真验证技术的可行性和定位性能。

1 单星多普勒定位算法

1.1 单星定位模型

在地心地固坐标系内，设接收机在t0时刻的空间坐标和速度为{Pre(t0),Vre(t0)}，此时到达接收机天线的卫星信号表示为s(t0)；若s(t0)从卫星发射出的时间为t1，卫星在t1时刻的空间坐标和速度为{Psv(t1),Vsv(t1)}，则满足:

(1)

式中,c为光速，σsv(t0)为信号传播路径中折射和多径等因素产生的测距误差，ε为接收机热噪声导致的测距误差。将式(1)改写为矩阵形式可表示为:

(2)

卫星与接收机的相对运动导致接收信号存在多普勒频移，若信号载波频率为f0，则信号s(t0)进入接收机天线的载波频率fre(t0)满足:

(3)

式中,矢量{rsv(t1),rre(t0)}分别为s(t0)在卫星和接收机端的传播矢量，由于信号传播过程中存在折射，因此rsv(t1)≠rre(t0)，且矢量差随着信号仰角的降低而增大。考虑卫星轨道高度在数百公里以上，且矢量差值有限，在此将式(3)近似为:

(4)

上式以矩阵形式可表示为:

(5)

公式两边对时间求导得到t0时刻载波频率变化率满足:

(6)

类似地，式(6)可表示为:

(7)

若接收机可通过其他手段获取自身瞬时的地心方向高度值Hre(t0)，可得到:

(8)

式中,re(Pre(t0))为接收机所在地域对应的地球半径，若接收机通过星历解算和修正获取{Psv(t1),Vsv(t1)}，并可通过其他传感器获取自身的Vre(t0)，则基于式(2)(5)(8)或者式(2)(7)(8)可得到关于接收机位置Pre(t0)=[xsv(t1),ysv(t1),zsv(t1)]T的三元方程组，通过解算可获取两个解值，去除一个镜像点可获得最终定位解。

基于伪距和多普勒的定位原理可表示为，基于高度Hre(t0)和伪距修正量可获得分别以地心和卫星为中心的椭球面和球面解系；基于多普勒获得了以卫星为顶点，以矢量Vsv(t1)-Vre(t0)为轴的锥面解系；这三个解析相交获得地球同面的一个镜像定位点和一个真实定位点。

1.2 粒子群搜索寻优计算

以式(2)(5)(8)为例进行迭代解算。将方程组进行线性化处理。将式(2)对Pre(t0)求偏导得到:

(9)

将式(5)变形为:

(11)

联合式(9)(10)(11)可得到在迭代值Pre,k-1处的线性化矩阵方程:

(12)

式(12)的最小二乘解表示为:

[Δxre,Δyre,Δzre]T=(GTG)-1GTb

(13)

与卫星导航中的最小二乘法相比，式(9)～(13)中减少了接收机钟差未知量和迭代更新过程，但增加了矩阵b关于地球半径信息re(Pre(t0))的更新过程。

在式(13)中，G阵受伪距迭代误差、多普勒观测和伪距模值的影响，由于伪距远大于接收机位置值，因此当多普勒表征不明显时，收敛域十分狭窄，初值不当将导致不收敛。为了解决这一问题，需要接收机具备较为精确的初值(如通过MEMS提供)或采用网格搜索方法实现初始的粗定位。网格搜索定位的原理为，在初始点P0附近按指定方式选取n个测试点P1～Pn，计算初始点、测试点与卫星位置的直线距离l0～ln及多普勒值d0～dn，在连续观测下将这些值和观测值按时间顺序求差，将连续观测点下的差值取欧式空间:

(14)

将欧式空间最小的点作为下次迭代的初始点重新迭代运算，直至欧式空间最小点不变即完成初始定位。

网格迭代中步长参数影响迭代效率和最终定位性能，步长选取过小将导致在有限的迭代周期内不能充分收敛，选取过大将导致定位精度较差。为达到理想值需要通过动态调整网格步长来提高定位性能，为此采用粒子群迭代寻优的方式对式(14)进行解算。这里首先介绍粒子群算法的原理和优化方式。

标准粒子群算法中粒子的速度更新和位置更新如式(15)和式(16)所示。

vi=ωvi+c1(pBesti-xi)+c2(gBesti-xi)

(15)

xi=xi+vi

(16)

式中，xi表示第i个粒子当前的位置，vi表示第i个粒子当前的速度。pBesti为粒子自身历史最优解又称个体极值；gBesti为整个种群的全局历史最优位置又称全局极值。c1和c2为学习因子，ω为惯性权重，其大小决定了粒子对当前速度的继承程度。

通常用Ns表示粒子群种群规模，记f(xi)为所优化问题的目标评价函数，粒子位置的优劣是依靠f(xi)的值来决定的。式(14)即为算法迭代求解的目标函数。得到粒子新的位置后，可以求出对应的f(xi)，并更新粒子的历史最优位置信息pBesti和种群的历史最优位置信息gBesti，每个粒子都根据这两个值来更新优化自己的速度和位置，然后继续迭代进行下一轮操作。

图1是粒子群算法在二维搜索空间求解优化问题的示意图。其中v1是粒子本身具有的速度，v2是粒子自身历史最优解引起的速度，v3是整个种群全局历史最优解引起的速度。粒子最终的速度v由v1、v2和v3共同决定，使得粒子从初始位置到达更新位置,并在后面迭代中逐渐靠近最优解位置。

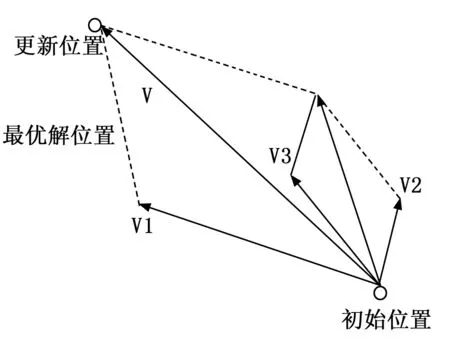
图1 粒子群算法求解二维空间优化问题示意图

可以通过粒子群算法的自适应调整策略来动态调整迭代的网格步长，具体为：连续迭代t次后判断粒子的位置改变程度，若小于某一个值则判断当前陷入局部最优阶段，采取增大网格步长的策略使得算法跳出局部最优；若连续t次迭代粒子位置改变都大于某一值，则判断粒子开始过快搜索，为防止粒子掠过最优解，采取缩小网格步长的方式压缩搜索空间。

自适应粒子群算法的迭代寻优步骤如下所示。

步骤一：设置算法参数，包括粒子种群数量Ns，最大迭代次数T，惯性权重ω和学习因子c1、c2及自适应选择策略中的参数t；

步骤二：给定初始个体最优位置pBest和初始全局最优位置gBest；

步骤三：开始迭代，根据目标评价函数评价邻域内所有粒子，与原有的个体最优位置pBest和全局最优位置gBest比较，选择目标评价函数较小的更新为新的个体和全局最优位置，利用公式更新粒子位置；

步骤四：重复步骤二和步骤三至t次迭代，若满足收敛条件或达到最大迭代次数则转步骤六，否则转下一步；

步骤五：判断粒子当前是否陷入局部最优或者进入过快搜索阶段，利用自适应参数调整策略增大搜索网格迭代搜索步长。返回步骤三；

步骤六：结束迭代寻优搜索。

2 单星参数观测方式

2.1 转发体制下的参数获取

接收机通过接收和测量星上转发的接收机应答信号实现测距，其过程表示为：接收机在tre,t时刻产生询问信号，经发送群延迟Δtre,e在天线端发送出信号；信号在tsv,r时刻进入卫星接收天线，经过转发处理群延迟Δtsv,e后转发回用户；接收机在时刻t0接收信号，经过跟踪解算得到接收时间tre,r。这一过程如图1所示，其中接收机初始钟差为δt，在时间周期trer-tret内钟差漂移为Δδt。

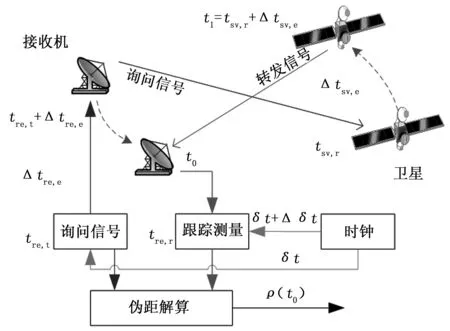
图2 星上转发伪距测量

在信号转发过程中，由于卫星和接收机运动分别在Δtsv,e和t0-tre,t-Δtre,e周期内产生一定位移，且传播介质具有时变性，因此上下行链路并不对称，将这一差异设为σsagnac，则接收机计算初始伪距为:

(17)

接收机在测距过程中并不受初始钟差影响，但需要预知或通过其他方法实时测量卫星转发器群时延和接收机收发通道的群时延，并对σsagnac进行适当的修正。在接收机获得初始伪距ρ(t0)后，通过卫星直接授时来估算时间t1，即:

(18)

2.2 双向体制下的参数获取

转发式测距下接收机无需预知本地钟差，但在有限的授时精度下对卫星位置的估计精度有限；一种提高定位精度的方法是通过双向测量与卫星建立高精度时间同步能力来进行测距和估计{Pre(t0),Vre(t0)}。如图2所示，接收机与卫星均在本地时为tre,t相互发送测距信号并彼此接收和完成测距，卫星将测距结果在下一次测距信号中返回给接收机。

图3 双向测距伪距测量

如图3所示，接收机和卫星获得的伪距分别为:

(19)

在此认为由于卫星和接收机的移动导致的上下行链路差异为σsagnac，则接收机计算本地钟差为:

(20)

在获取本地钟差后，接收机可基于ρre计算信号发送时间tre,t，并基于此修正伪距和计算{Pre(t0),Vre(t0)}。

3 单星多普勒定位性能分析

3.1 定位误差分布

若距离、多普勒频移和高度误差不对式(9)～(11)所示的线性化过程造成影响，则定位误差近似为:

(21)

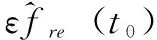
可以得到与星下点越远，等间隔的多普勒曲线越稀疏，而伪距曲线越致密；星下点轨迹的多普勒曲线比外围更加致密。因此可得到定位精度的分布特点：

1)在星下点区域定位精度对多普勒测量误差相对不敏感，而对伪距测量误差较为敏感；

2)随着与星下点距离的增大对伪距误差敏感程度降低，而对多普勒测量误差敏感程度逐渐增大；

3)在同样的伪距距离下，越靠近星下点轨迹对多普勒误差越敏感。

4)除上述特点外，在星下点轨迹附近区域内接收机更加难以判别所处位置在星下点轨迹的哪一侧，迭代定位中将有可能定位到镜像点上，造成较大的定位误差。

即对于单星多普勒定位，不同区域定位性能不仅与接收机和卫星的空间分布特征相关，还与不同的误差项相关。

3.2 定位覆盖能力

在此暂不考虑测距过程对用户容量的限制，取接收机遮蔽角为θ，卫星高度为Hsv，则卫星对地覆盖半径为:

(22)

式中,re为地球半径。不同高度卫星对应的覆盖面积及最大可见时间如图5所示。

当满足无缝覆盖时，所需卫星数估测为:

N≤(πre/rsv)2/2

(23)

对于600 km高度卫星，所需的卫星总数达到100颗以上，但相对于满足4星覆盖，所需的卫星总数仍缩减了50%以上。

3.3 定位仿真结果

针对某单星轨道进行定位仿真，仿真中在轨道星下点同侧任意设置了5个观测站点，卫星轨道及观测站点分布如图6所示。

仿真中基于卫星和接收机位置计算实际几何距离和多普勒频移，以此为基础加上设定误差作为接收机的模拟观测值，其中取卫星轨道误差为10 m、测频噪声为10 Hz、测高误差为3 m。在迭代计算过程中取粒子群规模为Ns100，迭代次数上限T为100,惯性权重ω取0.9，学习因子c1、c2都取1.5，自适应网格步长调整策略中t取10。

图6 卫星轨道及观测站点分布

通过仿真得到不同时刻各站点计算的定位误差如表1所示。

表1 单星仿真定位误差 (m)

可得到在仿真环境下不同时刻定位精度存在一定差异，并且远离星下点的观测点定位误差较差，总体上单星定位精度在百米量级。

4 结束语

基于伪距和多普勒观测量可实现单星条件下的导航定位，在本文设计的定位方式下，单星定位精度与伪距和多普勒观测误差相关，误差分布呈现出对不同误差项的敏感差异。通过仿真初步验证表明基于伪距和多普勒测量能够达到百米量级的定位精度。未来将进一步探讨单星导航定位的应用前景和工程实现中的相关技术。