空间计算机存储单元容错性研究

龚 博,郑 晨,张洪源,刘 莉,王超杰

(北京宇航系统工程研究所,北京 100076)

0 引言

空间中的辐射特性对电子元器件影响较大，主要因为辐射环境中高能粒子(重粒子、质子、中子、X射线、γ射线等)对集成电路造成的破环，其中辐射总剂量(TID，total ionizing dose)和单粒子效应(SEE，single event effect)为主要的表现形式，近年来随着电子器件中的存储单元尺寸越来越小，TID效应几乎可以忽略不计[1-3]，但接近纳米级存储单元逻辑门和极低核心电压导致单粒子效应(SEE，single event effect)大大增强，SEE又分为单粒子翻转(SEU，single event upset)和单粒子锁定(SEL，single event latch)，本文主要是针对逻辑门翻转效应进行研究。

SEU是指半导体逻辑器件由于受到单个高能粒子撞击而使逻辑状态翻转的情况，这种情况造成的错误不是硬伤是可恢复的，因此也被称为软错误。空间计算机系统中SEU发生频率最高的是面积相对较大的存储器部分(例如外部SRAM)，同时CPU和接口电路中存储单元也有发生的可能(例如缓存，锁存器)。

传统的容错算法和容错方案只针对单粒子单位翻转，但是随着存储单元的工艺尺寸越来越小，核心电压越来越低，单粒子多位翻转的情况越来越多。Alsat-1小卫星的观测表明在其轨道上每天每一位存储单元发生单粒子翻转的概率约为百万分之一，其中80%为单粒子单位翻转，20%为单粒子两位翻转和多位翻转[4]，而UoSAT-12卫星星载计算机SRAM对单子翻转的在轨实验统计得出结论在LEO轨道的单子多位翻转占单粒子翻转总数5%～10%[5]，尽管数据不尽相同，但我们可以得出结论：MBU已经不容忽视。

目前国内外许多卫星、在轨飞行器都采用了硬件的冗余容错来实现对空间计算机外围的存储芯片的纠错和检错，实现方式有抗辐照加固、三模冗余，专用的EDAC芯片等，但这些方案都不适用于现代商业航天的发展模式，主要是因为抗辐射加固会大大增重，影响有效载荷重量，三模冗余无法解决多位翻转问题，而专用冗余芯片无法满足周期短成本低的要求，因此需要构建一种针对MBU的容错码解决方案，占用较少资源的同时提升纠错能力，从而达到计算机存储单元加固目的。

1 建立容错模型

因为空间高能粒子具有较大离散性和较低的密度，所以单粒子多位翻转除特殊情况外(例如遭遇太阳磁暴等宇宙环境，粒子密度短时间内骤增，导致高密度粒子流或多个粒子同时击中多个存储单元)一般指单个高能粒子造成多个存储单元翻转，这种情况的发生主要依靠两种方式，第一种为注入塌陷效应，指高能粒子以小入射角垂直于存储单元入射，产生的电荷扩散到互相相邻的位置，由于电荷的共享效应，造成邻位多位翻转，例如图1中的第二类和第三类。第二种为击穿效应，高能粒子以大入射角水平入射轰击并穿过多个存储单元造成多位翻转，例如图1中的第一类和第四类，均造成了相邻位逻辑翻转[6]；传统上认为由于能量限制第一类较多，而随着存储单元核心电压降低第二类同样值得重视。图1是存储单元多位翻转的矩阵示意图，水平方向为存储单元排列方向，垂直方向为存储单元照射方向。

图1 单粒子多位翻转示意图

目前市场上商用器件除部分采用物理临位和逻辑临位分开工艺的器件外，大多数存储器件都容易收到单粒子效应影响，因此需要通过试验模拟高能粒子轰击存储单元来建立容错模型，图2是几组对比试验[7-9]，能量单位为MeV，取4个档位，并运用大量样本分析统计数据，从试验结果我们可以得出当用不同能量的质子轰击SRAM存储单元时可以造成大量的多位翻转，从存储矩阵的横列和纵列来看多位翻转几乎全部是相邻两位，相邻三位虽然存在但数量较少，四位及四位以上几乎可以忽略不计，由此可以得出模型中重要能力：容错能力要求在保持纠正1位检测两位错误的基础上能纠相邻2bit和3bit错误。

图2 单粒子多位翻转测试结果

容错模型的容错能力提出后还需要找到合适的容错方法，抗辐照加固、专用芯片前文已经提过不适应于现在的发展状况，我们主要考虑硬件冗余和信息冗余两种方法，硬件冗余中常见为三模冗余、多模冗余、逻辑冗余等，由于前文得出需要纠2bit、3bit的能力，经典三模冗余无法完成，多模冗余和逻辑冗余完成需要构建大量重复逻辑资源，造成体积、重量、成本等增加同样不适合于商用航天，另一种方案是信息冗余，信息冗余是通过某种算法(既冗余位和有效位的对应关系)来对信息位进行校验和纠错，信息冗余的优点是冗余度相对较少，所占资源相对较少，适用于本文需要解决的问题，但传统的以海明码为算法的EDAC(error detection and correction)算法同样不具有纠2bit、3bit的能力，不使用专用芯片的情况下需要构建一个算法来完成信息冗余方案。

2 构建信息冗余算法

信息冗余算法指在发送端按照某种特性构造增加一些冗余位，当数据有效部分和冗余部分因外界故障注入时发生错误，接收端按照同样的构造特性进行计算和比对，这种构造规则即为冗余算法，也就是常说的纠错码。由上文建模结果可知，我们需要一种抗MBU多位翻转的纠错算法。

因考虑工程实现的简便性，本文所讨论的编码算法均为二进制码，设输入的每组信息码的码元为k，经过编码后的每组码的码元为n，其中n>k，通常用(n,k)来表示。要构造编码算法首先要确定编码类型，这里我们需要选择最简单的线性编码，即在有效的8位或16位数据后面通过逻辑加法增加冗余位，线性编码能最大的节省寄存器资源，否则采用复杂编码算法就需要专门开辟寄存器存储区域来专门运行和存储计算结果，不但提高了成本和资源占用且会造成计算和存储的时间延迟。

由上文纠错模型可知，传统基于海明码和扩展海明码的EDAC算法纠错能力不足，无法应对商用器件空间环境下的MBU，需要我们重新构造编码算法，在线性编码的条件下完成纠错能力的提高，从工程实现和理论分析两个角度出发必须满足以下几个条件：首先，此纠错码必须为系统码，即保持有效位不变，也就是说从工程实现的角度来考虑有效的8位或16位在编码译码的过程中保持不变，减小工程实现难度；第二，从编码原理上分析，提高纠错能力必然意味着码距的增加，但通过上文建模可知，多位翻转并不是随机的，而是在存储阵列纵横的邻位翻转，这样我们只需要解决邻位翻转问题即可，码距增加的越小，编码的复杂程度越低，编码和解码所占用的资源和时间越少，越有利于工程实现；第三，此算法需要具有(n,8)的结构，因为现在工程上信息位基本均为8的倍数，使用(n,8)的结构可以最大程度增加冗余而又不影响工程上8位、16位、32位数据的使用，否则数据拼接这一项额外环节就会对系统造成额外负担。

现假设信息码原码为U，编码后的监督码为C，则C与U的关系可以描述为：

C=U·G

(1)

G即为生成矩阵，解码时公式如下：

H·CT=0

(2)

进行解码时H矩阵就叫做校验矩阵，也叫做监督矩阵，校验矩阵的各行是线性无关的，H矩阵与生成矩阵的关系如下：

G·HT=0

(3)

也就是所给定纠错码的情况下，编码和解码的线性关系就唯一确定了。由上可知H矩阵不仅确定了信息码和冗余码之间的关系，也决定了码的距离特性，实际上我们就是在用H矩阵在2n的码字中进行筛选。

设R是接收端接收到的码字，此时R中已经含有错误图样，仍然用校验矩阵H来检查码字是否满足校验方程，设编码码字C=(c6,c5,c4,c3,c2,c1,c0)，错误码字为E=(e6,e5,e4,e3,e2,e1,e0)，则R=C+E。收到R后用H矩阵进行校验，如下所示：

H·RT=H·(C+E)T=H·CT+H·ET

(4)

由方程(2)可以知道H·CT=0，带入方程(4)得H·RT=H·ET，设S矩阵为：

ST=H·RT=H·ET

(5)

则S就被称为伴随式或校验子，根据校正子和错误图样对应关系表查找对应错误。

本文在一种纠正相邻错误(15,9)的循环码的基础上进行改进[10-12]，这种码是系统码和线性码，可以纠正相邻2位和3位错误，这种(15,9)的循环码的生成多项式为g(x)=x6+x5+x4+x3+1，它的校验矩阵H如矩阵(6)所示。

(6)

对比上文几个必要条件我们得出：此码为2进制线性码，具备工程实现方便的特点，此码码距为3，虽然能纠正邻位错位，却不具备检测任意2位错位的能力，需要重新构造，增加其码距，提高其容错能力，同时，此码不满足(n,8)结构，我们也需要对其重新构造，使其符合我们计算机常用存储单元数据位要求，这里以最基本的8位为例，其他8的倍数依此类推。

我们首先对其进行结构上的改进，删除第九列，码字变为(14,8)结构，H矩阵变为矩阵(7)，使其满足我们结构上(n,8)的要求，但是其码距仍然为3，通过计算要检查任意2位错位同时保持纠正邻位错误码距至少为4，考虑到工程实现上的复杂程度，考虑提高码距为4。

(7)

原码字数据D7D6D5D4D3D2D1D0共计8位，根据校验矩阵(7)得出增加冗余码后码字的长度变为14位，设为D7D6D5D4D3D2D1D0C5C4C3C2C1C0，其中C5C4C3C2C1C0为冗余码，通过公式C·HT=0来约束，同时设S为伴随式，共计六位，为S5S4S3S2S1S0，我们通过公式S=E·HT得出伴随式S，计算结果可知伴随式不是一一对应，重叠情况如表1所示。

表1 改进校验矩阵对应的伴随式重叠表

伴随式共6位，含义如下：C2表示C2位单个错误，D50表示D5和D0位都出现错误，D210表示D2、D1、D0三位邻位错误，而C2和D50对应同一个伴随式值，表示伴随式重叠，即纠错码无法分辨这两种错误，同理D654、D71和D30表示三种错误对应同一个伴随式无法完成分辨和纠错。

通过上表我们可以看到我们仍然面临以下几个问题：1)部分错误使用同一伴随式，这样就会使我们在工程计算上分辨不出原码或冗余码的故障来源于哪种错误，从而无法就行纠错；2)工程上实现的意义仅在于纠正或检验出原码的正确与否，而冗余码出错也可以忽略，但此伴随式冗余码却占用者一定资源。

为解决以上两个问题，我们进一步分析可以发现D31D70这样的错误虽然是两位错误重叠，但我们仅仅要求检测两位，纠正相邻两位和三位，而不要求纠正任意2位，所以D31D70这样的错误我们工程上不关心可以忽略不计，同时我们发现所有重叠的错误中由于矩阵本身的性质导致均为奇偶重叠，即一位错误与两位错误伴随式相同，两位错误和三位错误伴随式相同，并没有一位错误与三位错误伴随式相同的情况，因此我们很自然想到在重叠的基础上用奇偶来区分，增加一列奇偶区分列，可以使码距由3变为4，满足检测任意两位的同时也保持了纠正任意一位同时纠正相邻两位、三位错误的能力，因此我们调整后矩阵H如矩阵(8)所示。

(8)

第二次改进矩阵求出的伴随式重叠统计如表2所示。从表中分析我们得出任意一位、相邻两位和相邻三位都不重叠，且任意两位可以检测，因此我们得出结论：改进后的循环码保证纠正1位检测2位错误的基础上针对MBU的错误模式满足了纠正相邻2位和3位的能力的要求。

表2 改进校验矩阵对应的伴随式重叠表

3 工程设计与实现

工程上我们可以根据改进后的H矩阵求出编码方程和解码的伴随式方程。电路实现时所需要的逻辑运算都是三种基本运加逻辑异或运算，这种逻辑电路通过可编程逻辑器件来实现，且可以根据不同的算法做出相应修改，具有很好的灵活性。以8bit为例得出编码计算公式和伴随式计算公式分别如公式(9)和公式(10)所示。

C6=D7⊕D6⊕D4⊕D3⊕D2⊕D0

C5=D7⊕D4⊕D1

C4=D7⊕D6⊕D5⊕D4⊕D2⊕D0

C3=D7⊕D5⊕D2⊕D1

C2=D5⊕D4⊕D1⊕D0

C1=D6⊕D5⊕D4⊕D3⊕D0

C0=C6⊕C5⊕C4⊕C3⊕C2⊕C1⊕

D7⊕D6⊕D5⊕D4⊕D3⊕D2⊕D1⊕D0

(9)

S6=C6⊕D7⊕D6⊕D4⊕D3⊕D2⊕D0

S5=C5⊕D7⊕D4⊕D1

S4=C4⊕D7⊕D6⊕D5⊕D4⊕D2⊕D0

S3=C3⊕D7⊕D5⊕D2⊕D1

S2=C2⊕D5⊕D4⊕D1⊕D0

S1=C1⊕D6⊕D5⊕D4⊕D3⊕D0

S0=C0⊕C6⊕C5⊕C4⊕C3⊕C2⊕C1⊕

D7⊕D6⊕D5⊕D4⊕D3⊕D2⊕D1⊕D0

(10)

EDAC容错原理图如图3所示，在CPU和存储器之间增加EDAC模块，由可编程逻辑器件FPGA实现，处理器和存储器之间除了地址总线相连外其他控制信号和数据信号均通过EDAC模块处理后再发给存储器，即对存储器的读写均由FPGA完成。

图3 EDAC模块设计原理图

两片存储器芯片分为数据RAM和校验RAM，分别用来存放数据码和编码模块生成的冗余码。其中addr1、addr2分别连接数据和校验SRAM，addr3连接FPGA实现EDAC模块，数据16位分为高8位和低8位，DATAH为高8位数据原码，PARITYH为高8位数据校验码，低8位同理。EDAC模块被分为平行的两部分，一部分对高8位数据进行校验，一部分对低8位数据进行校验，两部分数据位和校验位存储到四片SRAM中，4片SRAM的地址都由CPU统一控制，FPGA只对存储器进行数据的读写。

EDAC实现模块内部结构图如图4所示，其中EDAC模块负责连接CPU和SRAM之间的数据流，对于CPU来说SRAM是透明的，当片选信号有效时，写信号过程如下：wr/rd读写控制信号置1，三态门A打开，CPU发出数据经过三态门进入编码器，生成纠错码，此时多路选择器打开，数据码和纠错码通过三态门B写入存储器。当片选信号有效时，读信号过程如下，wr/rd读写控制信号置0，三态门B打开，需要校验的数据由存储器进入锁存器，由FPGA内部的时序控制器发出锁存信号sr_en将数据锁存，纠错模块将锁存的数据就行校验，并在读过程结束时由时序控制器发出是否有错的信号error，如果没有错误将数据通过三态门A送到CPU，如果有错将多路选择器打，将纠正后的数据通过三态门B回写入存储器。

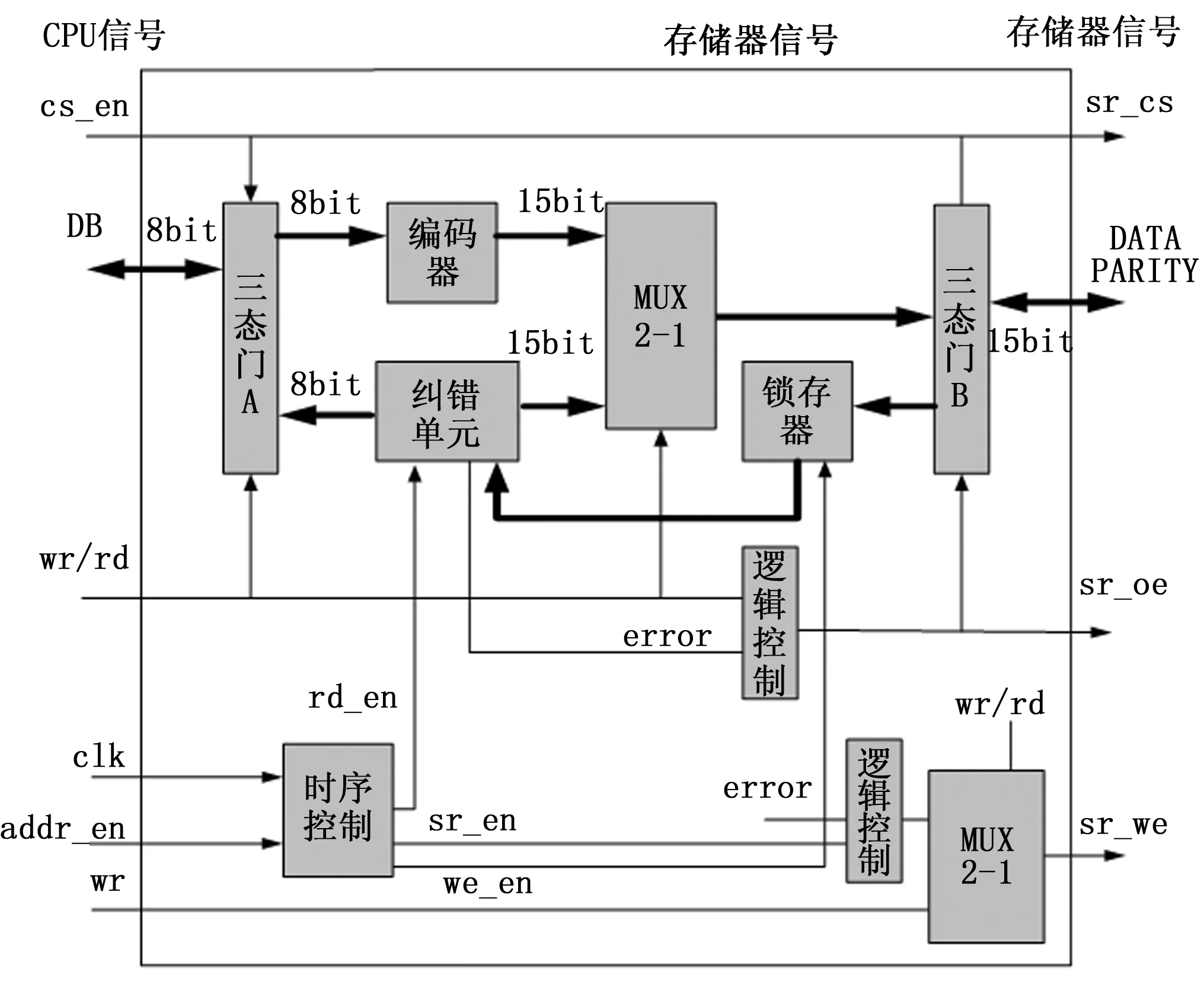
图4 EDAC内部结构图

时序控制器产生纠错结束标志信号cr_over，锁存标志信号sr_en，写控制信号we，具体操作如下，首先是锁存信号sr_en的产生，根据CPU数据手册，CPU地址总线使能最大延迟为20 ns，片选使能延迟也约为20 ns，而本系统中片选信号通过FPGA还要有约为5 ns的延迟，而从地址有效到数据有效的时间约为15 ns，从外部通过三态门B到锁存器的延迟约为5 ns，一共延迟约为20+5+15+5=45 ns，加上一些余量锁存时间确定为60 ns可以确保采到有效数据，纠错模块的逻辑电路延迟约为12 ns，取80 ns可以确定纠错完成时间，cr_over信号置1，如果发生错误数据还要回写至存储器，存储器最小写入时间约为18 ns，加上通过三态门的约为5 ns的延迟，约为80+18+5=103 ns，取120 ns为最后结束时间，所以we信号从80 ns至120置1，其他时间置0。

4 测试与仿真结果

本节将改进型循环码、扩展海明码以及准循环码进行仿真、测试和结果比较，比较他们的纠错能力和消耗的资源。

扩展的海明码、准循环码、改进的循环码功能仿真图如图5、图6、图7所示。clk是系统时钟，clkinsert是采样时钟，是验证环节错误注入需要的，cstate和nstate为两段式状态机的两个状态，din为输入数据，paritycode为编码数据，parityerror是软件注入的错误，s代表生成的伴随式，dataout为输出，e为最后检查出的错误，warnning为不能解决错误向CPU发出的中断请求信号。

图5 扩展的海明码编码解码仿真图

图6 准循环码编码解码仿真图

图7 改进型循环码编码解码仿真图

三种算法的纠错能力和资源消耗的总结如表3所示，其中实现资源中的S指Xilinx FPGA基本单元Slice，L指4输入查找表LUT，此表以8bit数据为例，所以存储资源1byte用来存放数据码，1byte用来存放冗余码，三种算法均为2byte，而时间延迟为布局布线加上时序约束后仿真软件的报告中给出的可能的最长的时间延迟路径。通过表中比较我们可以看到三种算法可靠度都非常高也都比较接近，而我们是通过FPGA并行实现的编码，所以码率在工程实现中的影响不大，时间延迟的技术指标为20 ns，三种算法也都满足了指标要求，最后我们看到新算法相比较与传统的海明码来说纠错能力有大幅提高，同时实现资源也相应增加，我们可以得出结论，新算法达通过面积资源的消耗换取了纠错能力的提升。

表3 三种算法纠错能力与资源消耗比较比较

5 结束语

本文通过资料分析得出空间环境下单粒子多位翻转模型，然后以此模型为基础提出一种改进型准循环码算法用于解决多位翻转下的相邻位翻转问题，最后以模型和算法为基础提出具有工程意义的EDAC纠错模块设计，并给出测试和仿真结果，结果证明本方法简单可靠，适用于工程应用，有效解决了商用存储器件空间环境中单粒子多位翻转问题。