基于最大相关峭度解卷积与形态滤波的齿轮故障特征提取

张 鑫，朱良明，崔伟成

(1.海军装备部 装备项目管理中心，北京 100071；2.海军航空大学，山东 烟台 264001)

0 引言

齿轮作为机械传动的关键部件，广泛地应用于火炮、导弹发射装置随动系统及雷达天线的自动瞄准跟踪中[1]。但由于运行环境恶劣及自身工艺、结构的问题，故障率较高；同时，故障监测、诊断不易实施，制约了武器装备维修、保障工作的开展。齿轮发生故障时，其故障特征反映在振动信号中，而加装振动传感器对装备运行几乎没有影响，因此，通过振动信号分析进行故障特征提取及诊断是一种可行的方法。

齿轮故障振动信号分析中，故障特征提取是核心。在工程中，希尔伯特(Hilbert)包络分析是最经典的方法，通过Hilbert变换对信号解调求取包络，对包络信号求取频谱得到包络谱，进而通过包络谱确定故障的有无及类型。但齿轮故障振动信号具有非平稳、非线性和信噪比低等特点，直接Hilbert包络分析往往不能充分提取故障特征。因此，在噪声背景下准确地提取出周期性的冲击特征是齿轮故障特征提取的关键[2]。

最小熵解卷积(minimum entropy deconvolution，MED)最早由Wiggens于1978年提出[3]，它以最大峭度作为求解滤波器的迭代终止条件，能起到突出信号中的冲击特征的作用，已成功应用在旋转机械的故障诊断中[4-6]。但MED只是突出冲击特征，而不是周期冲击特征。针对其不足，McDonald等在2012年提出了最大相关峭度解卷积(maximum correlated kurtosis deconvolution，MCKD)[7]。该方法以周期性脉冲为解卷积目标的需要，可根据故障周期的先验知识，对非整数故障周期进行预处理。MCKD方法可以恢复故障信号中的周期性冲击成分并起到降噪的作用，在轴承、齿轮箱故障特征提取及诊断中得到了成功的应用[8-11]，但解卷积信号Hilbert包络谱中故障特征信息表现仍不够明显。

数学形态学(Mathematical Morphological)由法国数学家Matheron等于1964年提出[12]。最早用于岩石学分析，由于其在非线性信号处理和分析上的优势，随着进一步地研究和发展，数学形态学被广泛应用于生物、图像识别、工业检测等多个领域。由于基于数学形态学的形态滤波方法可以增强冲击特征成分，在旋转机械振动分析及基于振动的故障特征提取领域得到了相应的关注，并取得一些有益的成果[13-15]。但数学形态滤波在故障信号微弱的振动信号分析条件下容易失效。

为了更有效地提取齿轮故障特征，本文提出了基于MCKD和数学形态滤波的齿轮故障特征提取方法。首先，将齿轮故障振动信号进行MCKD降噪处理，突出故障信号中的周期性脉冲；其次，应用数学形态滤波方法对降噪后的信号进行滤波处理，同时起到包络解调的作用；最后，通过求取MCKD-形态滤波包络谱，在此基础上进行齿轮故障特征的提取。

1 最大相关峭度解卷积

MCKD的思想源于MED。MED方法是一种不需要任何先验假设的信号时域盲解卷积技术。该方法以最大峭度作为求解滤波器的迭代终止条件，能突出信号中的冲击特征，非常适用于像齿轮和滚动轴承裂纹、点蚀等具有脉冲冲击类故障的诊断[6]。但也存在如下问题：(1)MED方法只能得到单个脉冲的结果，而旋转机械故障特征多为周期性脉冲；(2)MED方法通过迭代计算得到一个满足条件的解，而非直接求得的最优解[7]。

McDonald等在2012年提出了MCKD[7]，该方法基于相关峭度(Correlated Kurtosis，CK)作为解卷积优化目标。周期信号yn的相关峭度定义为：

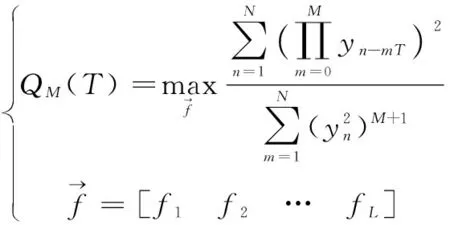
(1)

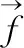
求解过程等同于求解方程，令：

(2)

求得的结果以矩阵的形式表述为：

(3)

式中,

MCKD的具体实现过程为：

1)选择周期T、滤波器长度L和移位数M；

6)若滤波前后信号的小于设定的值ΔQM(T)，则停止递归，否则返回(3)继续循环。

2 数学形态滤波

数学形态学的基本思想是利用结构元素在信号中不断移动，将目标信号在背景信息下的有用信息提取出来，以达到有效提取信号特征的目的[12]。设信号f(n)和结构元素g(m)是分别定义在Df=(0,1,…,N-1)和Dg=(0,1,…,M-1)的离散函数，且N≥M，则定义f(n)关于g(m)的4种基本运算[12]：

f(n)关于g(m)的腐蚀运算

(fΘg)(n)=min[f(n+m)-g(m)]

(4)

f(n)关于g(m)的膨胀运算

(f⊕g)(n)=max[f(n-m)-g(m)]

(5)

f(n)关于g(m)的开运算

(f∘g)(n)=(f⊕gΘg)(n)

(6)

f(n)关于g(m)的闭运算

(f·g)(n)=(fΘg⊕g)(n)

(7)

式(4)～(7)中，(Θ)为形态腐蚀，(⊕)为形态膨胀，(∘)为形态开，(·)为形态闭，且n+m∈Df，n-m∈Df。其中，腐蚀运算可以将信号的正脉冲特征抑制，保留负脉冲特征，膨胀运算可以将信号的负脉冲特征抑制，保留正脉冲特征；形态开运算可以将信号中的尖峰特征削尖，而形态闭运算可以将信号中的低谷特征填充。

利用上述4种基本运算可以构成最基本的形态滤波器。在实际的应用中，通过对基本运算的不同组合可以得到具有不同作用的形态滤波器。考虑到齿轮故障信号往往表现为同时具有正、负脉冲，为了准确提取故障特征通常使用形态差值滤波器。本文采用由腐蚀、膨胀运算构成的差值滤波器，即：

DIF(f)(n)=(f⊕g)(n)-(fΘg)(n)

(8)

一般而言，形态滤波的效果取决于结构元素的形态，结构元素的形态包括形状、幅值和长度3个要素，而同一结构元素对不同的冲击特征适应性又不尽相同，因此在无法获得故障信息的先验知识的情况下，采用直线型的扁平结构元素是更为合适和有效的，这种扁平结构元素不仅在一定程度上能直观准确地提取待处理信号的形状特征，而且能简化运算缩短时间。考虑到形态滤波的效果，本文方法中令结构元素的幅值为1，长度为冲击特征周期的0.2倍左右[12-15]。

3 故障特征提取方法及流程

在齿轮故障特征提取中应用较多的是数学形态学中的差值滤波器。该方法能对信号中的冲击特征明显增强，突出故障特征，从而有效实现脉冲特性故障信号的提取。同时形态滤波方法具有包络解调的作用，能替代Hilbert变换进行包络谱计算，避免了Hilbert的边缘效应。因此对故障信号进行形态滤波处理后，通过频谱分析可以更容易辨识故障频率。

但是，在实践中发现数学形态差值滤波器对具有明显脉冲的故障信号(呈超高斯分布)的检测效果较好，对无明显脉冲的故障信号(呈亚高斯分布)有时无法正确的检测出故障特征。究其原因，旋转机械故障初期脉冲冲击力较小，故障信号淹没于噪声信号中，数学形态差值滤波器无法辨识信号与噪声中的冲击成分，只是将综合信号的冲击成分增强。也就是说虽然形态滤波可以有效提取信号中的冲击特征，但也同时加强了噪声中的冲击成分。因此，直接应用形态滤波进行故障特征提取，所提取故障信号受噪声影响，经包络分析故障特征频率往往表现并不明显，容易造成误判，导致算法失效。

针对齿轮故障振动信号，MCKD方法能通过迭代有效实现周期性故障信号的提取。在对故障信号解卷积的过程中实现了对故障信号的降噪，但所提取故障信号受噪声影响，直接应用Hilbert包络分析，故障特征频率往往表现并不明显。

为了达到准确故障诊断的目的，结合MCKD和数学形态滤波的特点，本文给出了一种新的齿轮故障特征提取方法。对含有大量噪声的齿轮故障振动信号，首先应用MCKD方法进行预处理，达到对周期性冲击特征增强和提高信噪比的效果；然后对降噪信号应用数学形态滤波，进一步增强故障的冲击特征，并解调出振动信号的包络；最后应用经典的包络分析方法进行齿轮故障诊断。

该方法对MCKD和数学形态滤波组合使用，前者对信号降噪可以在一定程度上避免噪声中冲击成分对故障特征提取的影响，后者作为一种解调方法，并可以增强信号中的冲击特征以提高信噪比。有效避免了：1)受噪声影响，MCKD方法所提取故障信号不明显；2)应用Hilbert变换进行解调，受Nuttall定理的限制以及FFT能量扩散造成的端点效应问题[16]；3)故障信号中如果含有大量噪声成分，经形态滤波后会造成故障特征和噪声中的冲击成分相互混杂致使无法辨识故障特征频率。

基于MCKD和数学形态滤波的齿轮故障特征提取方法具体的流程见图1。

图1 基于MCKD与形态滤波的齿轮故障诊断流程图

1)对采集到的振动信号进行初始化处理，包括去均值处理，中值滤波、均值滤波等简单的去噪。

2)对初始化处理后的信号进行冲击特征周期计算及包络分析，校核MCKD的周期T、滤波器长度L和移位数M等参数选择是否合理。

3)对齿轮故障振动信号进行MCKD，实现故障信号的降噪及增强对原始信号中的周期性的故障冲击特征的效果。

4)对故障特征增强信号计算冲击特征周期等关键特征，校核形态滤波结构元素的幅值、长度等参数选择是否合理。

5)利用形态差值滤波器对得到的故障冲击成分进行滤波处理，使冲击成分进一步增强，同时起到包络解调的作用，得到包络；

6))对包络信号求取FFT，得到MCKD-形态滤波包络谱。

7)根据齿轮传动轴的转速及齿数，计算各齿轮的转频，根据包络谱在齿轮的转频及其倍频的谱线特征，得到齿轮正常、剥落、磨损、电蚀及裂纹与断裂等结论。

4 试验数据分析

依托QPZZ-II试验平台系统进行基于MCKD与形态滤波的齿轮故障诊断方法的验证。该试验平台可采集齿轮振动信号直接运用成熟方法进行信号分析和故障诊断，并可将数据以文本格式导出，便于深入研究。系统装配了大、小两级圆柱齿轮，大、小齿轮的齿数分别为75、55，模数为2。

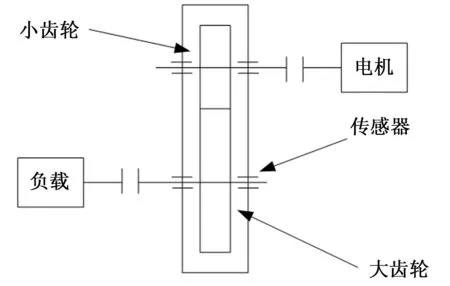
图2 试验平台结构简图

试验中对试验平台配置的小齿轮进行了故障处理，模拟了小齿轮断齿故障。在调速器中将电机转速设置为880 r/min，通过传感器测得实际转速871 r/min，由图2可知小齿轮的转频等于电机轴的转频，以实际转速计算，可以得到为小齿轮转频约为14.5 Hz，按照两个齿轮的齿数比，可计算大齿轮的转频约为10.6 Hz，此时，试验平台传动系统的啮合频率为797.5 Hz。设置数据采样频率为5 120 Hz，采样2 s的齿轮故障振动信号作为原始数据，即数据点数为10 240。

图3给出了实验数据的时域波形、频谱及Hilbert包络谱。在图3(a)的时域波形中可以发现原始信号有周期性冲击信号，但波形相对杂乱。图3(b)的频谱中可以找到5个明显的共振频带，但不易找到故障特征的信息。在图3(c)的包络谱中，可以发现14.5 Hz及29 Hz处存在较为明显的谱线，14.5 Hz、29 Hz为小齿轮转频的1倍频和2倍频，可以给出小齿轮故障的结论，但谱线的幅值与噪声成分的幅值相差不大，高次倍频成分也并不明显，即故障特征不够明显。

图3 原始信号的时域波形、频谱及包络谱

用本文的方法进行齿轮故障特征的提取。首先，对信号进行MCKD处理，MCKD的参数设置为：滤波器长度L为300，周期T为353，迭代次数为30，移位数M为1。然后，应用形态滤波方法进行降噪、解调处理，将形态滤波结构元素设为直线，长度设为70。最后，对包络信号求取频谱，得到如图4所示的MCKD-形态滤波包络谱。

图4 MCKD-形态滤波包络谱

由图4可以看出：1)在小齿轮转频的1倍频14.5 Hz、2倍频29 Hz、3倍频43.5 Hz及4倍频58 Hz处均存在清晰的谱线；2)14.5 Hz及29 Hz处谱线的幅值较图3(c)中相应谱线的幅值明显增大；3)58 Hz～200 Hz高频段的噪声明显得到抑制。因此，MCKD-形态滤波能明显增强齿轮故障振动信号的故障特征。

作为对比，首先，按照相同的参数设置对原始信号进行MCKD处理，求取Hilbert包络谱列于图5。从图5可以看出：1)14.5 Hz、29 Hz、43.5 Hz及58 Hz处均存在相对清晰的谱线；2)14.5 Hz、29 Hz、43.5 Hz及58 Hz处谱线的幅值较图4相应谱线的幅值明显偏小，14.5 Hz、29 Hz处谱线的幅值比图3(c)相应谱线的幅值还小；3)高频段的噪声比4处故障特征频率处的谱线还突出。在本算例中，从故障特征提取的角度来说，单纯MCKD的效果，还不如直接求取原始信号的Hilbert包络谱。

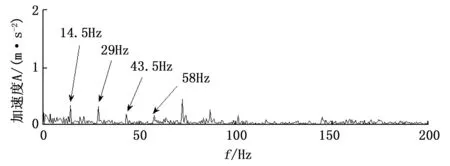
图5 MCKD包络谱

然后，应用相同参数设置的形态滤波方法求取原始信号的包络，将包络谱绘制于图6。从图6可以看出：1)14.5 Hz、29 Hz处均存在清晰的谱线；2)14.5 Hz、29 Hz处谱线的幅值较图1(c)相应谱线的幅值大；3)43.5 Hz、58 Hz处未发现明显的谱线，无法获得更多故障特征的信息；4)高频段的噪声较小。综合来看，直接形态滤波处理的效果优于MCKD、Hilbert包络分析，但不如MCKD-形态滤波。

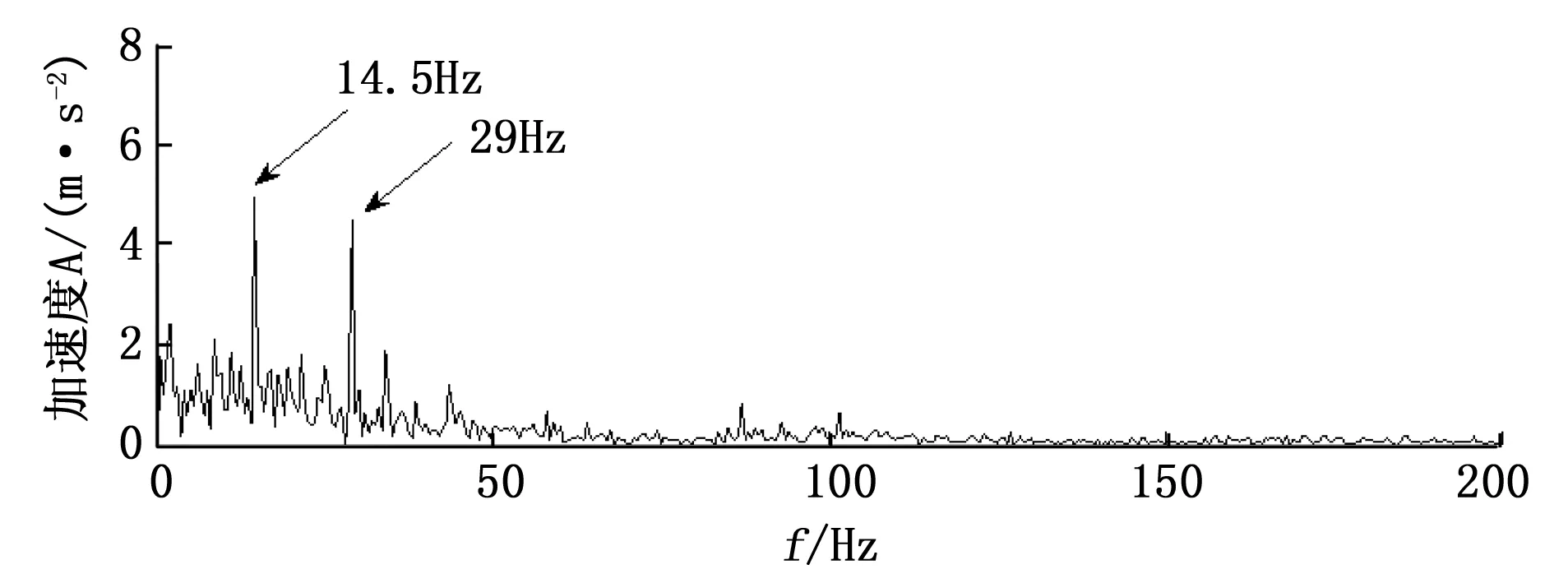
图6 形态滤波包络谱

最后，形态滤波包络应用MCKD方法增强周期性脉冲，MCKD方法参数设置不变，将脉冲增强后的包络求取傅里叶变换，得到形态滤波-MCKD包络谱并绘制于图7。从图7可以看出：1)14.5 Hz、29 Hz处均存在清晰的谱线；2)29 Hz处谱线的相对幅值较图4相应谱线明显，14.5 Hz处谱线的相对幅值较图4相应谱线弱；3)43.5 Hz 处谱线不明显，58 Hz处发现明显的谱线；4)高频段存在较多的明显谱线，该频段的谱线不便于进行故障分析，这是由于形态滤波包络信号中残余的噪声具有脉冲特征，MCKD方法将相应的脉冲特征放大，导致高频段谱线杂乱。从效果来看，形态滤波-MCKD不如MCKD-形态滤波，即MCKD与形态滤波方法组合使用时，应将MCKD作为信号预处理方法，将形态滤波后置。

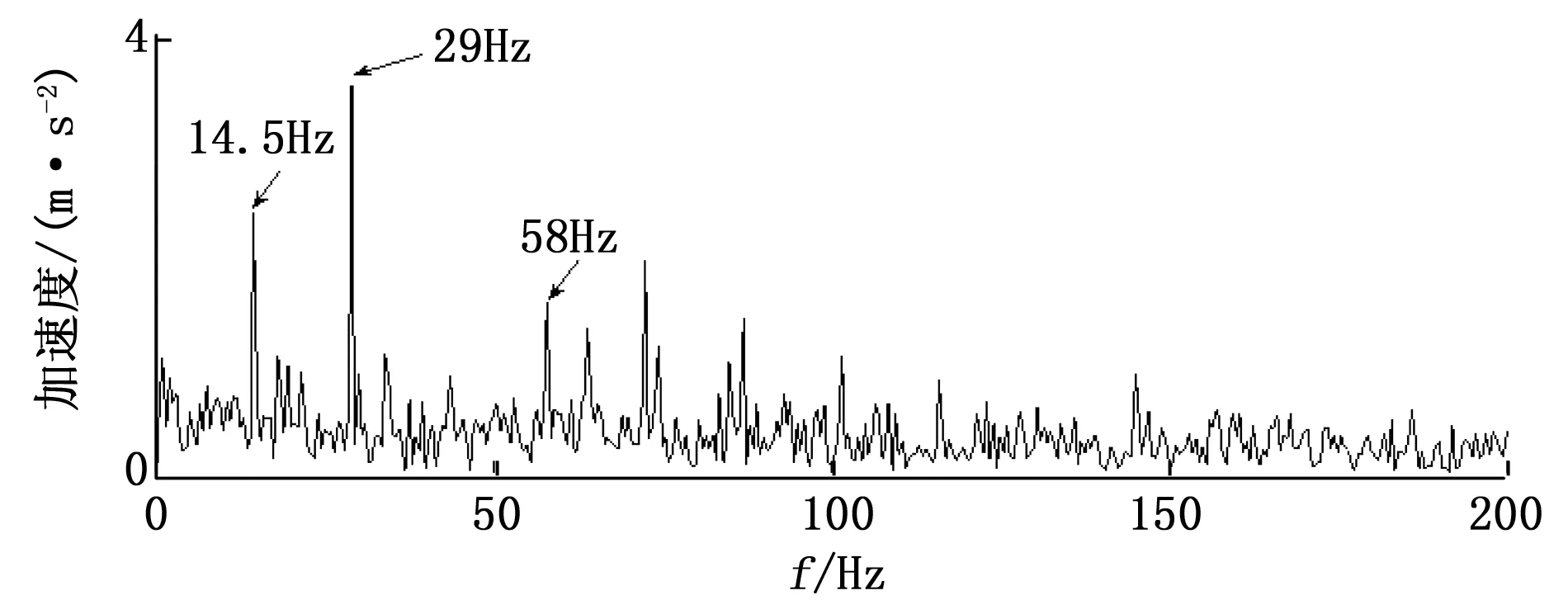
图7 形态滤波-MCKD包络谱

通过对比Hilbert包络分析、MCKD、形态滤波和形态滤波-MCKD对故障信号的处理结果，可以看出，MCKD方法可对故障信号降噪，对降噪后的信号进行形态滤波处理可以在一定程度上避免噪声中冲击成分对故障特征提取的影响。整个结果表明本文方法具有良好的齿轮故障特征提取效果，MCKD-形态滤波方法具有合理性和有效性。

5 结束语

本文结合MCKD与数学形态滤波，给出了一种新的故障特征提取方法。综合利用MCKD对周期性冲击的恢复能力和差值滤波器的冲击特征增强及解调能力，明显增强了冲击类故障振动信号的故障特征。以齿轮断齿故障振动信号为例，验证了方法的有效性。为齿轮乃至其它旋转机械类故障特征提取、故障诊断等方面的研究提供了新思路。