近二十年我国数学问题提出研究知识图谱分析①

陈汉君 杨 蕊

(天津师范大学教育学部 300387)

爱因斯坦说过，提出一个问题比解决一个问题更重要．数学问题的提出是推动数学及其相关领域发展的根本动力[1-2]．希尔伯特提出了20世纪数学家应当努力解决的23个数学问题，这些问题被认为是当时数学的制高点，有力地推动了20世纪数学的发展，在世界上产生了深远的影响．在数学教育中，数学问题的提出不仅是数学问题解决的先决条件，更是相对独立的数学教育活动[3]．20世纪中后期，数学教育界在经历了“新数”运动和“回到基础”以后，提出了“问题解决”思想．20世纪90年代以来，“问题提出”作为一种重要的数学活动[4]，逐渐成为独立的研究课题，受到广大数学教育研究工作者的重视．近年来，国际数学教育界越来越多地关注“数学问题提出”，我国《义务教育数学课程标准(2011年版)》和《普通高中数学课程标准(2017年版)》均将“学生提出问题的能力”作为课程总目标之一；2010年，美国《州际共同核心数学课程标准》中也提出要培养学生的数学问题提出能力．为了厘清“数学问题提出”研究的发展状况、研究热点和未来方向，研究采用内容分析法和文献计量法，对我国近20年“数学问题提出”的成果进行梳理分析，探寻我国“数学问题提出”的研究特点，为更好地开展“数学问题提出”相关研究提供参考．

1 研究数据与方法

1.1 研究数据

在中国知网(CNKI)，以“问题提出”与“数学”为主题词，对2000年至2019年(共20年)发表的期刊论文进行了检索，截止时间为2019年12月27日，共得到文献582篇．剔除会议纪要、书评等非数学教育研究论文，得到有效文献542篇．用Refworks格式导出并对数据格式进行转换，获得用于绘制知识图谱的原始数据．

1.2 研究方法

借助CiteSpace软件，结合每年的发文数量和期刊类别，使用内容分析法梳理研究主题，再从论文关键词和研究主题的演变等方面绘制知识图谱，得到“数学问题提出”的发展脉络、研究热点和未来发展趋势．

2 研究结果

2.1 “数学问题提出”是20年来数学教育研究的持续研究热点

对2000—2019年来关于“数学问题提出”发文数量的统计，如图1所示．总体来看，近20年来有关“数学问题提出”的研究论文数量整体呈现上升趋势．

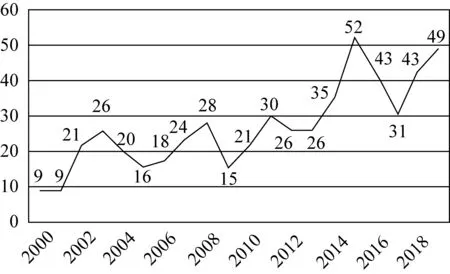
图1 近20年“数学问题提出”研究发文量变化趋势图

进一步研究分析，近20年“数学问题提出”研究发文大体可以分为两个阶段：

第一阶段是2000—2009年，这一阶段发文数量稳中有升，但整体增长速度不快且不同年份之间的波动较大．究其主要原因是，学界对“数学问题提出”这一研究领域的重要性尚未达成共识，很多研究具有脉冲式特征，在某些时点较为集中而在其它时间则发文较少．如2003年《普通高中数学课程标准(实验)》将“数学地提出、分析和解决问题的能力”作为五大拓展能力融入三维目标的表述之中[5]，激发了研究者对“数学问题提出”的研究热情，研究数量有所增加[6-9]．

第二阶段是2009—2019年，这一阶段发文数量呈现明显的上升趋势，虽然在2017年出现较大幅度回落，但是在2018—2019两年发文数量又接近历史高点．这一变化趋势说明在这10年间，“数学问题提出”这一研究内容已经逐渐成为学者们的共识和研究热点，研究热情仍有逐年上升之势．

2.2 《数学教育学报》和《数学通报》在推动“数学问题提出”研究方面发挥了核心期刊的作用

关于“数学问题提出”的研究主要发文期刊有171种，其中教育类综合性期刊有70种，数学教育类期刊有24种，大中专院校学报有54种，其它期刊有23种(如表1)．从发文数量上看，数学教育类期刊发文数量最多，平均发文量为10.5篇，约是其它类型期刊平均发文量的4～8倍．相关论文发表数量排在前20位的期刊有《数学教育学报》《数学通报》《数学学习与研究》《中学数学》《数学教学通讯》《课程教育研究》《中学数学月刊》等，其中数学教育类期刊有14种，教育类综合性期刊有6种．从期刊年平均发文数量上看，数学教育类期刊关于“数学问题提出”的论文平均每年发表的数量不足1篇，而其它几类期刊的年平均发文量更少．

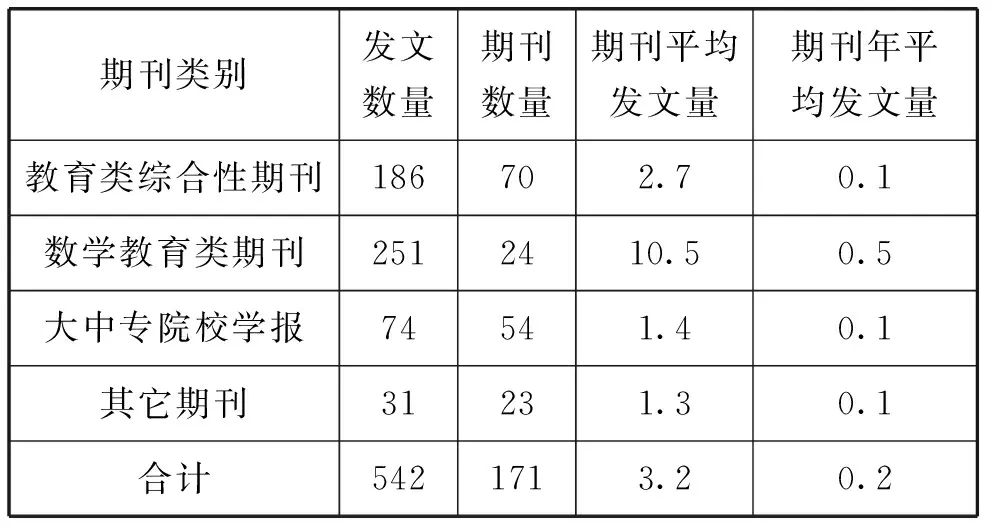
表1 近20年来“数学问题提出”研究的发文期刊类别统计

在全部171种发文期刊中，北京大学《全国中文核心期刊要目总览》(简称核心期刊)中的期刊只有12种，占期刊总数的7%，核心期刊文章发表数量占发文总量的17%．在这些核心期刊中，发文数量排名前三的是《数学教育学报》(56篇)，《数学通报》(14篇)，《教学与管理》(9篇)，其余期刊发文量均为1～2篇(如表2)．核心期刊的平均发文量是7.7篇，年平均发文量为0.64篇．

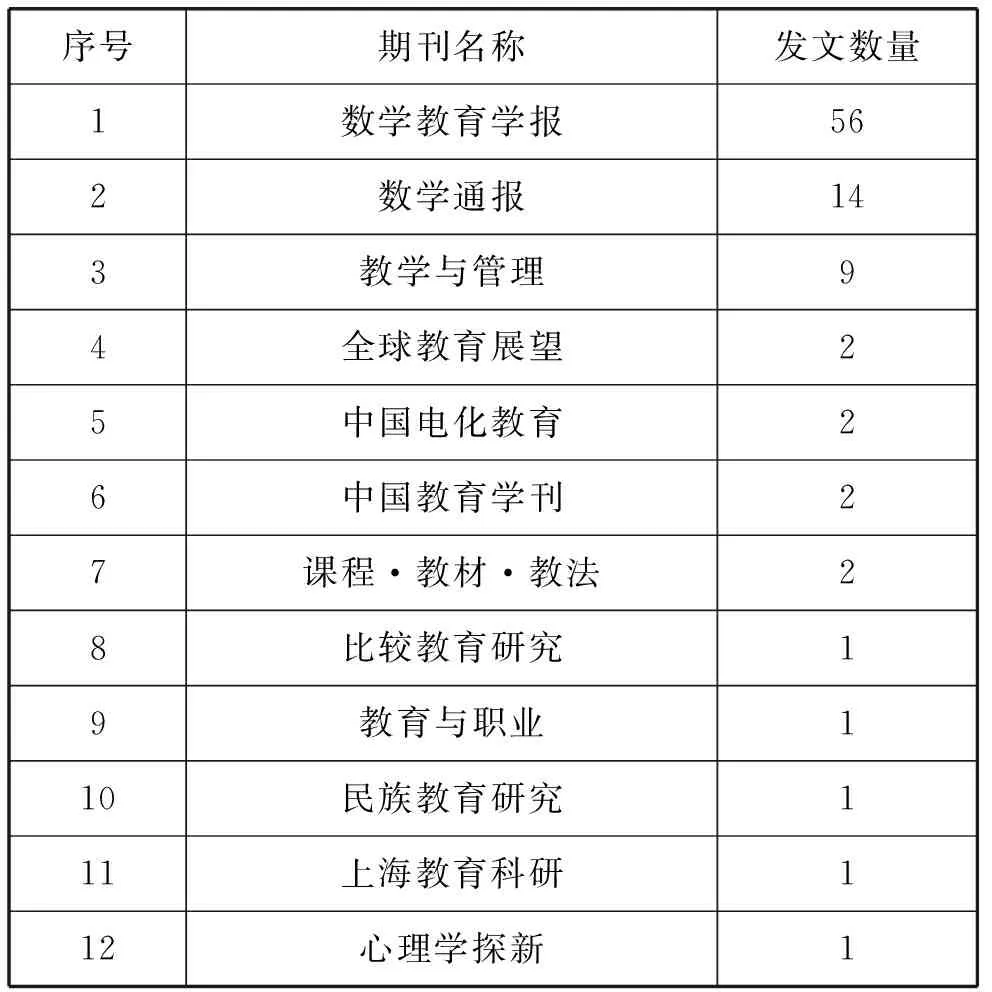
表2 核心期刊发文情况

关于“数学问题提出”研究的论文刊发期刊分布较为广泛，主要为教育类期刊，其中数学教育类期刊的发文量最大．《数学教育学报》和《数学通报》所发相关论文占核心期刊发文量的76%，在推动“数学问题提出”研究方面发挥了核心期刊的作用．总体而言，有关该主题的研究成果在核心期刊种类及发文数量上仍然偏少，研究水平和层次还需要进一步提高．

图2 关键词知识图谱

2.3 提出问题、数学问题、数学教学和问题提出是研究的热点

关键词是对论文内容的核心提炼和表达，通过关键词及频次分析可以直观的了解到研究的热点分布．利用CiteSpace软件绘制关键词知识图谱(见图2)．

分析发现，提出问题、数学问题、数学教学和问题提出等4个关键词出现的频次均超过50次，是研究的热点．这也表明在统计时段内，研究者们关于“数学问题提出”的探讨还是以整体思考为主．“数学情境”出现频次较高与贵州师范大学研究团队的系列研究关系密切[10-12]；有关学生“提出问题能力”的研究也受到研究者的广泛关注[13-17]；针对“数学问题提出”本身的解构分析，诸如问题意识、提问策略等的研究成果不断出现[1，6-7]，引领着该课题研究向新的方向发展；围绕“培养学生、中小学生、高中数学”等的关键内容是由“数学问题提出”的派生结果，表明“数学问题提出”要围绕“数学”，以“学生提问”为中心．另外，有关“数学问题提出”的综述研究[4，18]，对关键词频次的贡献比较全面，有助于梳理课题研究脉络．

2.4 “数学问题提出”经历了由理论探讨到深入实践的研究历程

在对“数学问题提出”研究过程中，不同主题的研究起始时间和离散程度也不尽相同．使用CiteSpace软件研究主题聚类中的时间线统计功能得到了较为详尽的结果，如图3所示．

图3 研究主题的时间演变

分析发现，在该研究领域共涉及13个大的研究主题，分别是提出问题、问题提出、平方差公式、数学问题、数学情境、高中数学、数学问题提出、学生提问、三角函数、数学创新、圆锥曲线、中考数学和教学模式．

这13个主题虽然都是该研究领域的关键内容，但是在时间线上的演变特征并不相同：提出问题、问题提出、数学问题、数学问题提出和三角函数等主题受到关注较早，目前仍为研究的热点；近一两年，有关平方差公式、数学情境、高中数学、学生提问、数学创新、圆锥曲线等主题的研究成果减少；中考数学和教学模式两个主题在2004年前曾被广泛研究，此后受关注较少．这些研究主题之间的切换，与数学教育的整体研究方向不无关系．“问题提出”和“提出问题”这两个相近的概念主题，在文献统计起始的2000年便已出现，并且具有十分高的研究热度，近20年间始终热度不减并且经过了充分的演化过程．而像三角函数、教学模式等主题不仅首次出现的时间较晚，并且其随着时间的演化过程也相对简单．这表明对“数学问题提出”主题而言，研究的核心内容从宏观的“问题提出”概念与实质的探讨开始，不断探索“问题提出”研究的意义，进一步深入到结合诸如平方差公式、三角函数、圆锥曲线等具体数学知识内容，达到方法论层面，概括出问题提出的有效策略，呈现出从关注教育理论到关注教学实践的转变，从思辨分析向实证研究的转变，它们共同构成了对“数学问题提出”的研究脉络和框架．

3 思考与建议

通过CiteSpace软件的聚类分析可以发现，数学问题提出的相关研究主题分布广泛，主要包含了13大研究主题和研究热点，不同的研究主题在近20年的时间维度上又具有不同的发展特征，表明各研究主题在不同的时间受到的关注程度不尽相同．虽然近20年该研究领域成果不断，但研究主题的分散性导致研究的逻辑性和系统性不强，并且在当前核心素养引领的教育改革背景下，“问题提出”如何服务于学生核心素养的发展，也需要研究者厘清研究脉络和思路、突出研究重点，通过进一步聚焦“数学问题提出”开展理论探索与实践应用研究，使研究逐步走向系列化、深入化、专题化．

教师是学生成长的引路人，学生“问题提出”意识和能力的培养离不开教师的正确引导．在数学教学中，教师首先应做到具有创造性提出问题的意识和能力，不仅要认真准备高质量的、能启迪学生思维的数学问题，更要带领学生共同发掘和搜集教学过程中生成的数学问题，进一步引导学生提出有新意的“真问题”,让提出有价值的数学问题成为学生的自觉行为[19]．教师善于将实践教学中出现的新问题、新思考作为“数学问题提出”研究领域主题演化的根本动力，指导“数学问题提出”的教学实践走向深入，通过建立良好的师生正向反馈机制，在提高教学实践效果的同时提升教育研究的水平．国家要提升学生“问题提出”的意识和能力，就应该加大力度培养智慧型教师队伍，努力把教师自身的数学知识转化为教学智慧，从而更多服务于学生数学学科核心素养和能力的提升，促进学生的可持续发展，真正突破唯分数、唯升学的桎梏，实现教育家叶圣陶提出的“教是为了不教”思想．

“数学问题提出”的重要性已为广大数学教育科研工作者和一线教师形成共识，有关“数学问题提出”内涵的讨论也相当丰富[1，20]．但专门针对如何提升“数学问题提出”质量、如何进行测评和改进的文献还不多见，这应该成为今后研究的焦点．当前中小学课堂教学中提出的问题，存在指向不明、流于形式、思维价值不高、为了提问而提问等情况，问题提出的质量也参差不齐．今后可以开展高校教师与相对固定的中小学一线教师的长期合作研究，既可以弥补高校学者实践经验的不够丰富，又可以提升一线教师的理论水平，实现教育研究的落地．另外，把发现问题、提出问题、分析问题和解决问题当作一个不可分割的整体[21]，在问题解决系统中来评价数学问题的质量，从而提高数学问题提出的质量，推动数学问题提出的教学测评和改进．同时，我们需要开展跨学科研究，融合并挖掘不同领域的研究视角和方法，为一线教育实现有效协同创新教育提供依据．