基于多变量非线性DAE子系统模型的同步发电机励磁汽门综合控制

陈蓓玉 岳华 屠壮

0 引言

对于实际电力大系统,被控对象(如元件)往往是电力大系统中的一个非线性微分-代数(Differential-Algebraic Equations,DAE)子系统,受系统其余部分产生的关联输入变量的影响[1-3]．针对单输入单输出的非线性DAE电力系统,已经有了许多成果．文献[4]将非线性常微分方程(Ordinary Differential Equations,ODE)系统的Lyapunov方法扩展到了非线性DAE系统,给出了非线性DAE系统稳定的充分条件;文献[5]研究了基于非线性DAE子系统模型描述的电力系统的可逆性;文献[6]设计了一个多指标的非线性励磁控制律,增强了系统的稳定性,提高了发电机机端电压控制精度;文献[7]建立了多机系统下含STATCOM的DAE模型并运用目标全息反馈方法,设计出STATCOM与励磁的分散协调控制律;文献[8]则针对存在随机扰动情况,研究了带随机扰动抑制的同步发电机励磁控制器设计,实现了系统稳定;文献[9]利用模糊变结构方法,设计了同步发电机的励磁控制器;文献[10]则将反步自适应方法应用于同步发电机励磁控制,实现了对系统未知参数的估计,使得闭环系统稳定.

然而,同步发电机的励磁汽门综合控制问题,却是由多变量非线性DAE子系统模型来描述的,其系统内部变量之间以及输入输出之间的非线性耦合关系更为复杂,其控制问题并非单变量情形的简单扩展就能解决,而关于此类控制问题的研究还不多见．文献[11]针对MIMO非线性DAE系统,扩展了非线性ODE系统的微分几何方法,提出了M导数、M括号概念,并将其应用于交直流并联系统非线性控制器设计;文献[12]则研究了MIMO非线性DAE子系统的逆系统控制方法,提出了一种递归算法,实现了系统的输入输出线性化解耦.

本文扩展了非线性常微分方程系统的反步控制方法,研究了由多变量非线性DAE子系统模型来描述的同步发电机励磁汽门综合控制问题．首先若被控系统的向量相对阶存在,那么可通过一个微分同胚和反馈控制,实现系统的解耦和等价转化．接下来基于等价系统,利用反步(backstepping)方法设计出其镇定控制器[13],使得整个闭环系统渐近稳定．最后基于MATLAB进行了仿真,仿真结果表明了本文所提方法的有效性.

1 系统的数学模型

同步发电机励磁汽门综合控制描述为如下的双输入双输出非线性DAE子系统模型[12]:

(1)

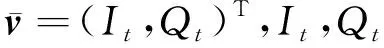
(2)

可以验证,在发电机正常运行范围内系统(1)满足如下两个性质:

性质1是指数1的,即代数方程g(·)关于代数变量z的雅克比矩阵具有常满秩:

(3)

本文的目标是对同步发电机多变量非线性DAE子系统(1)和(2)设计镇定控制器,使得闭环系统渐近稳定.

2 多变量非线性DAE子系统的向量相对阶和模型等价转化

2.1 非线性DAE系统的向量相对阶[12]

(4)

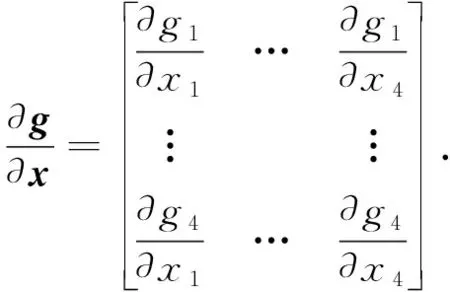
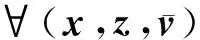
(5)

其中

(6)

(Ⅱ)矩阵

(7)

是非奇异的.

显然,本文中m=2．可以验证,系统(1)和(2)的向量相对阶存在,为(1,3)．步骤如下:

1)由式(6)可得:

LFs1LFfh2=LFs2LFfh2=0,

ω0Iqc3Id(xq-x′d)-ω0Iq(HT′d0)

(8)

2)由式(7)可知这里

(9)

在发电机正常运行范围内,有

(10)

综上,由定义1可知系统(1)和(2)的向量相对阶存在,为(1,3).

2.2 非线性DAE子系统模型的等价转化

定理1存在一个微分同胚和一个反馈控制,使得系统(1)和(2)等价转化为如下形式：

(11)

证明选取如下坐标变换:

(12)

由式(1)、(8)和(12)可得:

(13)

其中

(14)

显然选取反馈控制

(15)

可将系统(1)和(2)等价转化为

(16)

其中r1,r2分别是待设计的新的控制项．证毕.

由定理1,系统(1)和(2)被解耦为两个子系统,便于进一步的控制设计.

3 镇定控制器的设计

定理2若等价系统(11)满足如下结构特性:

(17)

那么系统(1)和(2)是可渐近稳定的.

证明

(18)

其中c1,1>0是设计参数.

2)下面利用反步设计方法,考虑第2个子系统

(19)

的镇定控制.

第1步.定义误差变量

e2,1=ξ2,1,e2,2=ξ2,2-α2,1,

(20)

其中α2,1为待设计的第1个虚拟控制器．由式(19)与式(20)可得:

(21)

(22)

其中c2,1>0为设计参数.

第2步.如此继续,设直到第3个定义误差变量

e2,3=ξ2,3-α2,2,

(23)

(24)

(25)

至此,对整个误差闭环系统取Lyapunov函数为

V=V1+V2.

(26)

由式(18)、(25)和(26)可得:

(27)

可知整个闭环误差系统是渐近稳定的．证毕.

4 多机电力系统仿真

下面选择图1所示的两区域四机电力系统进行仿真研究,不妨选取机组G1为被控对象.

系统运行方式为:初始时系统双回线稳态运行,0.5 s时线路7—8中的一回线k处(仿真中k=0.1)发生三相对称接地短路,故障中的对地电抗为0.000 1 pu,0.65 s故障切除,系统恢复到初始运行状态．机组G1采用本文所提控制方法,控制参数选取为c1,1=10,c2,i=20,i=1,2,3．G1的输出响应如图2和图3所示.

由图2和图3可以看出,反步镇定控制器取得了良好的控制效果,保证了发电机功角以及输出机端电压的稳定性,G1的输出渐近收敛于系统稳态值.

5 结论

本文针对同步发电机多变量非线性DAE子系统模型,通过扩展多变量非线性常微分方程系统的L括号、L导数概念,实现了系统的解耦和等价转化,在此基础上运用反步设计方法,设计其镇定控制器,使得整个闭环系统渐近稳定．与孤立多变量非线性DAE系统的精确反馈线性化方法相比,本文的研究结果更具一般性．所提出的模型等价转化方法不仅适用于电力系统,同时也适用于其他领域非线性DAE系统的控制问题研究.