一种在DEM平地中的河网水流方向估算方法
董良,张宏鸣,王岩泽,詹淇茹,樊晓
(西北农林科技大学 信息工程学院,陕西 杨凌 712100)
0 引言
在区域尺度研究中,基于数字高程模型(digital elevation model,DEM)获取河网、汇水面积、坡度等相关地形特征时,都需要提取水流方向[1]。通常,原始DEM经填洼处理[2],加之地形本身的特征,平地面积会占有很大的比例。由于平地高程一致,快速、有效获取其流向一直是比较棘手的问题[3]。在国内外关于流向的计算方法研究中,O’Callaghan等[4]提出的坡面流模拟方法D8(deterministic eight-neighbors)算法应用最广,即在3像素×3像素的DEM 栅格上,计算中心栅格与各相邻栅格间的距离权重高程差,差值最大的栅格为中心栅格的流出栅格。而在平地流向提取时,无法明确水流方向。
关于平地流向的计算,一些研究者先后提出了各自的方法。Jenson等[5]提出的方法(J&D)在后来许多研究中得以应用,也被集成到ArcGIS等软件中。该方法根据平地出口点向平地内部迭代确定平地栅格流向,每次迭代需遍历所有DEM栅格,处理效率较低,且结果易产生“平行流”问题[6]。Martz等[7]采用高程增量叠加的方式修改平地DEM,确定研究区域内的水流方向。之后,Garbrecht等[8]又改进了高程增量的计算方法,G&M方法有效避免了平行流问题。
Barnes等[9]基于G&M方法将平地的增高处理分为3个部分,先计算平地与出口的距离,再计算平地与边界的距离,最后叠加这2种距离,得到平地高程增量。在此基础上,又有研究者做了进一步推进,如使用链码矩阵(CCM)[10]和距离变换(DT)[11]方法来确定平地区域的流向。Liu等[12]采用3种不同的高程增量修正平地,第一级和第二级增量分别用来确定平地出口点和平地中心的流向,第三级增量通过重新修正区域内高程值来确定流向。尽管减少了DEM增量,但反复修正DEM值,效率还需进一步提升。此外,修正DEM的方法也会破坏地形形态,影响地形特征的提取质量[13]。
国内很多研究者还提出了其他方法来确定平地流向。Kong等[14]认为在输入的等高线资料中,根据地形图资料增加能够反映地表起伏的高程信息,避免平地和洼地出现,但这会使地形地貌发生形变,影响地形特征的提取质量。Zhang等[15]采用径向基函数插值法确定每个栅格的高程增量,利用数字信道网络结合周围地形的高程来确定平地流向。Pan等[16]通过线性插值的方法来修正DEM值,从而用D8算法计算平地流向。赵美玲[17]提出在平坦区域结合实际水系,修正主干河道高程,使整个区域水流有序向流域出口汇流。Yu等[18]改进了Wang等[19]方法中由于填洼重新生成平地的问题,并且通过修改平地DEM值计算其流向。此外,Wu等[20]在综合了FD8算法[21]和Rho8算法[22]的基础上,从多流向和地形随机性因素2个方面对流向算法进行了改进。Zhang等[23]提出了结合非平地区域流累积值的MW方法来确定流动方向。夏誉玲等[24]提出的混合流向算法将数字地形分类后,对缓坡和鞍部区域采用多流向算法确定径流方向,并进行水量分配,能大幅减少非自然的平行径流。
上述方法大多参考平地周围高程值,获得的流向几乎一致,易产生平行的流线,无法提取清晰而独立的河网。而对平地采用逐级抬高增加高程来构造微坡面的方法,使得平地流向处理效率不高,并且DEM的微小变形可能在平地周围出现洼地,对结果产生较大影响[13]。
本文在前期研究的基础上[23],提出以平地栅格的初始汇流累积量为参考,采用最短路径方法和就近原则方法来计算平地的水流方向。本研究直接对平地进行流向判断,不需对DEM进行修改,通过与J&D方法、Barnes方法对比,用所提出方法提取流向结果合理并效率较高,具有较好的运行效果和可行性,是对数字地形分析方法的有益尝试。
1 平地处理的方法介绍
1.1 平地处理的基本思想
在数字流域特征提取中,形成数字河网的关键环节之一是获取每个DEM栅格的单位汇水面积[25]。单位汇水面积是指其他栅格直接或间接流向一个栅格的汇流累积量(即累计流量)。通过计算非平地区域的汇水面积,平地最外圈的栅格会有初始累计流量,而平地内部栅格的初始累计流量则为0,这些平地区域便是河网提取中存在的断点。
一般在流域中,上游栅格的累计流量按照流向趋势逐渐向下游累积,逐渐增大,最终会形成一个数字河网。因此,在平地上游存在一个在平地区域中初始累计流量最大的平地栅格,将其视为平地水流的一个入口点;在平地下游有一个高程值大于周围非平地栅格高程的平地栅格,即有流向的平地栅格,将其视为平地的一个出口点。
为提取平地区域内的流向,可将其入口点和出口点之间的最短路径视为主流,从而确定主流路径上各栅格的流向。同样,将平地上游中初始累计流量次大的平地栅格作为支流入口点,计算该入口点到达平地中已分配流向栅格之间的最短路径,确定该路径上平地栅格的流向,该方法称为最短路径方法。需要注意的是,在某一平地区域中支流的个数不宜太多,否则会出现区域内流向散乱的情况,无法获得清晰的河网。而对于平地中未分配流向的栅格,或初始累计流量小于规定阈值的小流量栅格,使用就近原则方法,将其流向收敛于附近已有流向的平地栅格。
本文将前期计算DEM数据的平地栅格的初始汇流累积量和确定的平地出口点,作为使用以上2种方法的基本前提条件。由出口点找到待处理的平地,由初始累计流量的大小来确定使用最短路径方法或者就近原则方法。
1.2 平地处理的过程
平地处理总体流程如图1所示。图2表示某平地区域及周边非平地栅格的高程值。在平地处理前,需要使用D8算法确定非平地的流向,并找到平地的出口点,即平地下游边缘区域周边栅格高程值,低于该平地栅格高程值的平地点(图3),再由非平地流向计算其累计流量,便得到平地边缘栅格的初始累计流量。规定区分流量大小的阈值为8倍栅格长度,将平地中初始累计流量较大的栅格,依次作为平地区域的主流和不超过3条支流的入口点(图4)。对于平地中剩余的小流量栅格,采用就近原则方法,赋予其附近流域的流向。

图4 平地初始累计流量

图3 D8算法确定平地出口

图2 平地区域及周边栅格高程值

图1 平地处理总体流程
将这块平地中的所有栅格均处理完,再以相同的方法依次处理所有的平地。
1.3 大流量栅格最短路径算法
平地区域主流和支流的最短路径是一个简化的迷宫求解[26]的过程。从平地入口点开始按照宽度优先搜索的方法走到出口点,然后回溯确定路径,并分配给路径上各平地栅格的流向。所求最短路径首先满足包含最少步数的条件。
假设某2点间的路径由m条长度为1的直边和n条长度为1的斜边组成,该路径长度为L1;每减少k步斜边则增加2k步直边,得到路径L2;则有表达式如式(1)、式(2)所示。
(1)
(2)


图7 支流路径确定过程

图6 主流路径确定过程

图5 平地主流支流的路径

2)按照宽度优先搜索方法依次遍历每个节点,并计入辅助队列中。
3)按照步骤1)方法确定当前节点的子节点,以步骤2)方法不断遍历至平地的出口点(即有流向的平地栅格)后停止搜索。接下来从出口点回溯,寻找当前节点的父节点,并赋予其水流方向。
4)找到平地的主流之后,使用上述最短路径算法,从初始累计流量次大的平地栅格搜索到距离最近的主流路径上或出口点,确定支流及路径上的栅格流向。
1.4 小流量栅格就近原则算法
通过最短路径算法确定平地区域中主流和支流路径上部分栅格的流向之后,剩余未分配流向的都是初始累计流量较小的栅格。这些小流量的栅格在汇水过程中,不能形成独立的水流。为避免区域内出现散流、乱流现象,提出就近原则算法,将剩余未分配流向的平地栅格,收敛于附近的主流或者支流上。就近原则算法的具体步骤描述如下。
1)设置一个数组依次存放平地中已有流向的栅格。
2)遍历该数组中有流向平地栅格的8邻域,如果邻域中有尚未分配流向的栅格,则令其流向8邻域中间的平地栅格,并将此平地栅格加入该数组中。
3)按照步骤2)方法依次遍历数组中有流向的栅格,来确定其他未分配流向栅格的流向。当数组中有流向平地栅格数等于该平地总栅格个数时,处理完毕。图8(a)、图8(b)、图8(c)为就近原则方法的示意过程。

图8 无流向栅格就近原则
2 平地流向处理的实验与结果分析
2.1 实验数据和环境
使用4个地区不同规模的数据进行测试和分析。第1个是陕西省绥德县韭园沟流域,海拔高度851~1 103 m,平均高度980 m,占地总面积100 km2。第2个是陕西省安塞县县南沟流域,流域面积44 km2,海拔1 100~1 400 m,平均高度1 200 m。这2个区域地貌沟壑纵横,是典型的黄土丘陵沟壑区,侵蚀较严重。第3个是USGS官网上提供的SRTM1数据,澳大利亚中部(23.00°S,131.00°E~20.00°S,134.00°E)的9块SRTM数据,该区域中平地面积所占比重很大。第4个是贝加尔湖以东(47.00°N,112.00°E~56.00°N,121.00°E)的100块SRTM数据。
本算法在Visual Studio 2017集成开发环境下采用C#语言实现。运行于Windows10(64位)操作系统,CPU为Interl(R)Core(TM)i7,内存8 GB。为了和具有代表性的J&D方法、Barnes方法的计算结果进行比较,要确保程序运行环境一致。Barnes算法从其提供的下载站点获取,同本算法一样,每组DEM数据测试5次,取得平均运行时间,输入相同的DEM数据,输出计算后的栅格流向存储在一个文本文件中。将结果都导入ArcGIS 10.2软件中,用水文分析工具处理得到可视化的图层。J&D方法已集成在ArcGIS软件的水文分析步骤中,直接使用工具完成。
2.2 平地流向处理结果
实验中使用的10 m分辨率的韭园沟流域数据,局部沟谷存在连续的平坦区域,地形特征最具代表性。在平地处理前,直接对该地区进行流向和汇水的计算,在设置河网提取的阈值为500后,得到有断点的河网(图9)。经本算法处理平地后,确定平地区域的流向,进而计算汇水,可提取到完整的河网(图10)。

图9 韭园沟流域局部有断点的河网

图10 韭园沟流域局部完整的河网
2.3 同现有方法的对比和分析
本文和J&D方法、Barnes方法在处理结果的合理性和效率方面做出了比较和分析。为验证本文方法的普适性,从澳大利亚中部地区一块SRTM数据中分割出500像素×500像素的样区进行详细分析对比。该样区地形起伏较小,样区内存在较多平坦区域和缓坡(图11)。根据本文方法,对该样区进行流向计算,然后设置阈值提取河网(图12)。在相同河网阈值下,对利用J&D方法得到的结果(图13)以及Barnes方法得到的结果(图14)进行了分析和比较。

图11 澳大利亚中部地区500像素×500像素的样区

图12 本文方法对样区的河网提取结果
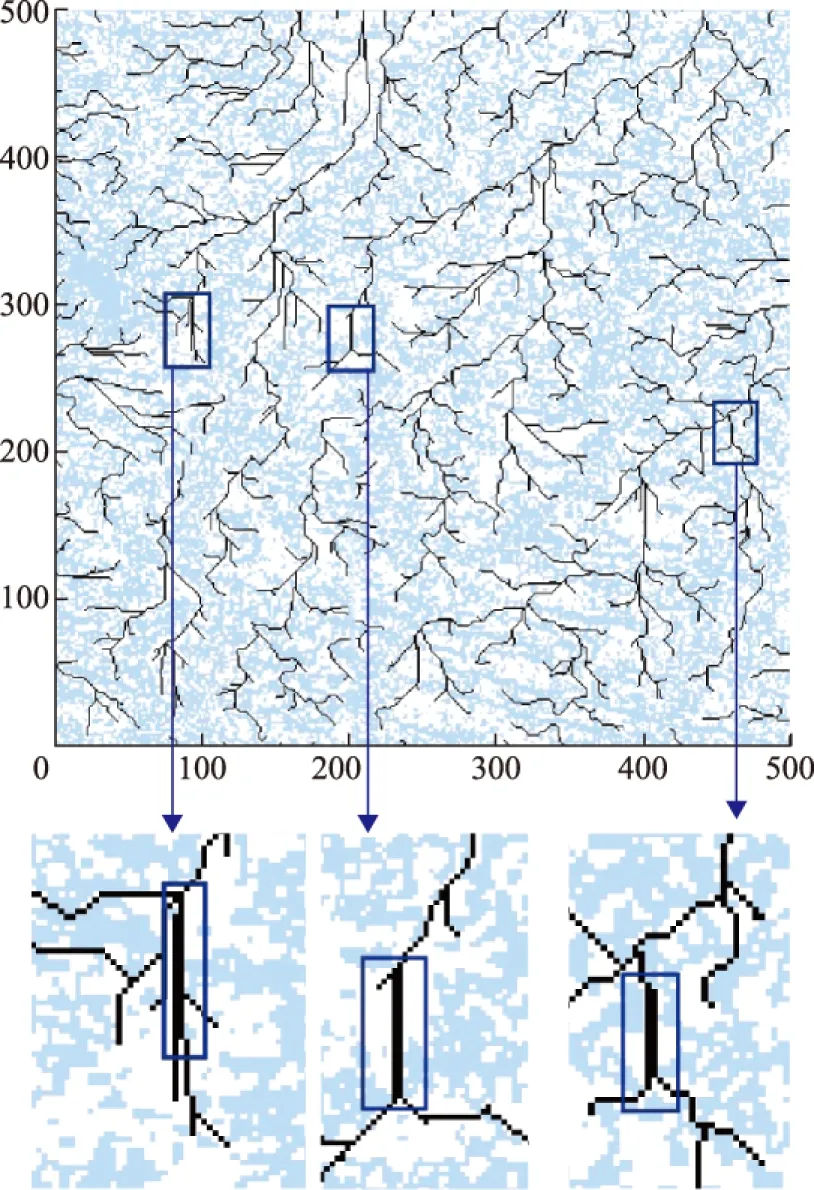
图13 J&D方法对样区的河网提取结果

图14 Barnes方法对样区的河网提取结果
J&D方法主要基于坡面流模拟D8算法,根据平地出口点向平地内部迭代来确定平地流向。而D8算法在实际执行过程中会规定一个8邻域的遍历顺序,最终确定的所有平地栅格的流向往往受遍历顺序的影响,所得平地流向方向相同,易产生大面积的平行伪河道。Barnes方法修正平地DEM数据,为平地设置高程增量,将其改为微坡面,然后依旧用D8算法确定流向。整个修正过程分为3步:①计算平地内部每个栅格与出口的距离;②计算每个栅格到边界的距离;③将2种距离进行累加,确定最终的平地高程增量。将平坦的区域重构为周边略高中心低、出口边更低的一个“微型沟谷汇水面”。这种方式在径流汇集处会得到不错的效果,减少了部分的平行径流的出现,但在平地的中心区域仍会有小面积的平行伪河道。
本文方法的提取结果其河网总体走势和上述2种方法的结果基本一致,而设置相同河网阈值后,得到的河网流线清晰,并无平行流产生。这是由于平地流向算法首先确定主流和支流最短路径,保证了水流路线的整体趋势,而对于小流量栅格的流向,采用就近原则收敛于主流支流,不会出现流向散乱的情况,总体分配合理。
在算法运行效率方面,本研究设计的算法需要前期计算DEM数据的非平地区域的汇水面积,同时找到所有平地的出口点以及对应的平地。在设计实现时,将计算DEM栅格数据的汇水面积和计算平地区域水流方向相结合起来,这里只分析平地处理部分。对于Barnes方法,相应地,也仅分析平地处理过程的效率。对不同地区、不同规模的数据,算法具体运行时间如表1所示。
通过使用不同特征的DEM数据进行测试,将Barnes方法和本文方法对比。从表1中分析发现,对于同一地区的不同分辨率的数据,分辨率下降时,DEM数据存储量减少,对应的平地数量相对减少,本文方法对所有测试数据的处理时间均小于Barnes方法,效率较高。Barnes方法对平地的处理过程主要在于修正DEM数据,需要计算2次高程增量再叠加,每次计算还需要遍历所有平地栅格;而本文方法直接进行计算,遍历一次平地栅格即可。在测试数据比较庞大或区域中平地所占面积比较大时,Barnes方法对内存空间的要求更高,这也是增加计算量产生的结果。本文方法计算简单,可行性较好。
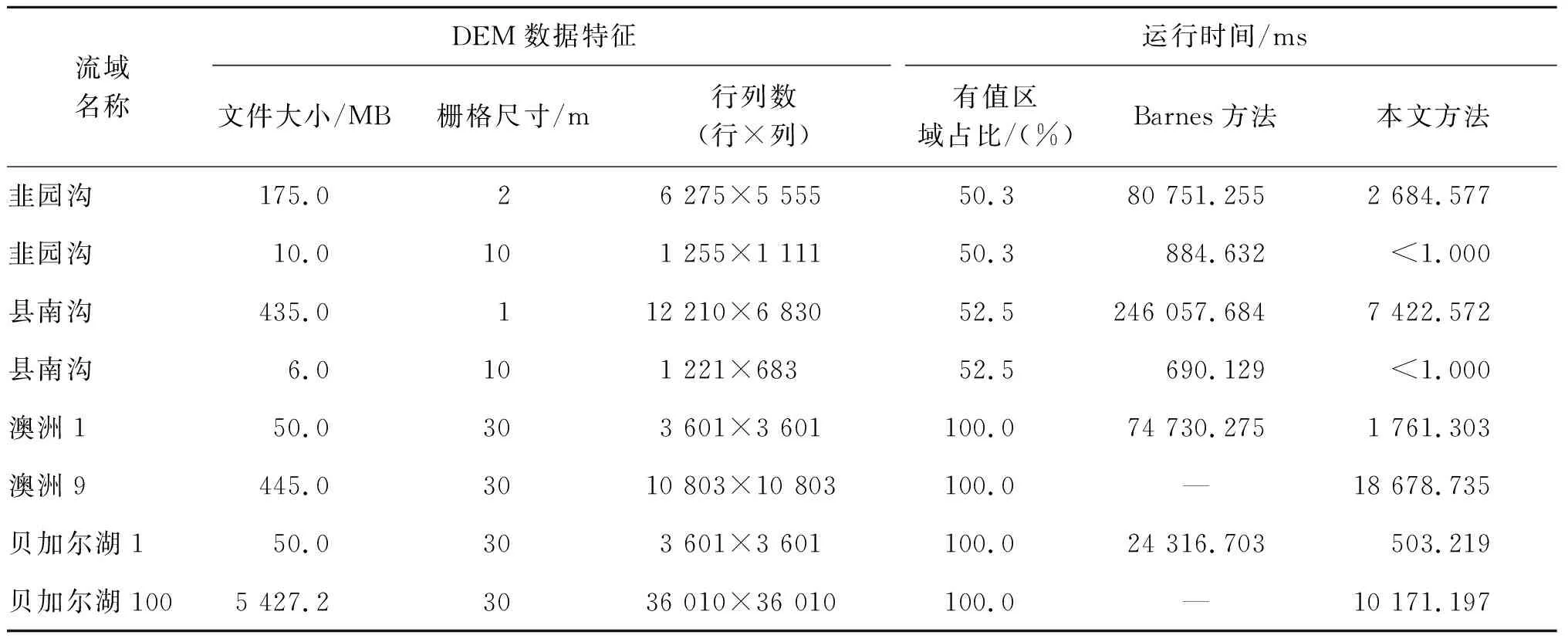
表1 不同数据、不同规模下的平地处理效率对比
3 结束语
DEM数据预处理是水文应用中的一个重要环节,只有合理确定水流方向,才能得到精度较高的河网水系及数字流域特征,为分布式水文模拟提供基础数据。基于DEM的水系提取,在地形起伏较大的山区等非平缓地区应用精度较高,但在平缓区域或人类活动影响较大的平原区还有待进一步探索,这也将该领域的研究推向热潮。
借鉴前人研究,在对流域分布式侵蚀学平地处理认识的基础上,进行理论分析和研究,设计并实现了平地水流方向处理的算法。本文主要与J&D方法、Barnes方法进行对比。相比而言,本算法得到河网的结果与以上2种方法基本一致,且几乎不存在不符合实际规律的平行流的问题。在运行时间上,Barnes方法通过修正平地DEM数据,2次计算平地的高程增量,再进一步将2种距离累加确定最终的平地高程增量,然后用D8算法确定修正平地后的微坡面的流向,这样不断重复计算和迭代,计算量很大,效率较低。而经过本算法的计算,可以明显看到平地中的主流,以及其他支流汇聚到主流之上,也解决了平地区域中部分水流方向散乱的问题,整体结果比较合理,无平行流产生。在运行时间上,本算法无须修正平地DEM数据,通过前期计算DEM数据的非平地区域的累计流量,同时找到平地的出口点和部分入口点,直接对其进行计算,运行时间短,效率较高。
综上所述,本处理方法利用DEM对平缓地区的数字流域构建,是平地河网提取方法的有益尝试,也是对数字地形分析技术的补充。

