基于PSO-BP神经网络盾构掘进参数预测研究

（中铁十六局集团有限公司，北京 100018）

珠海市位于海积平原与丘陵交汇处，广泛存在上部软弱、下部坚硬的软硬互层，复合地层中，不同地层岩石强度差异巨大，地层条件变化复杂，导致了盾构掘进参数差异性较大[1～2]。对于何种地层适用何种掘进参数，一直是盾构施工中的难点问题，若盾构参数选取不合理，将导致盾构姿态偏移、管片拼装质量差、管片错台漏水等严重质量问题[3～4]。

本文以珠机城际轨道交通横琴隧道1#工作井～湾仔北站盾构区间∅8.8m 复合式土压平衡盾构施工为例，针对区间典型地段的不同地层，根据已采集的盾构施工数据，采用粒子群优化算法对BP 神经网络算法进行优化，建立PSO-BP 神经网络盾构掘进参数预测模型，并对建立的模型和预测结果进行验证，该模型可以为同类地层条件下的盾构施工提供指导[5]。

1 PSO-BP神经网络理论

1.1 PSO-BP神经网络原理

在粒子群优化算法中，假设每只鸟作为一个粒子，该粒子具有独立行动的能力，并且具有随机的初始速度和初始位置，它就是适应度函数在解空间的一个解。众多的粒子在解空间中自由运动，共享搜集到的信息，根据每个粒子自身飞行经验和全局粒子的飞行经验进行迭代，最终达到种群的最优解，也就是目标函数的最优解[6]。

BP 神经网络算法结构中包含一个输入层、多个隐含层、一个输出层，及各层之间的连接权值与阈值。通常情况下，各层之间的连接权值与阈值采用梯度下降法进行计算，随之带来的问题是前期收敛速度慢、容易陷入局部最小值等[9]，为解决这一问题，采用粒子群优化算法对BP 神经网络的连接权值和阈值进行优化，从而建立PSO-BP 神经网络盾构掘进参数预测模型。

1.2 PSO-BP神经网络模型构建流程

建立PSO-BP 神经网络模型具体网络设计过程如下。

1）确定PSO-BP 网络结构和参数。

2）建立粒子群中各粒子与连接权值和阈值的参数映射关系。

3）确定粒子群算法中各粒子的参数。

4）更新各个粒子极值与全局极值。

5）粒子群算法终止并输出最优解。

6）建立PSO-BP 神经网络模型并进行预测。

75岁的张奶奶是济南市历城区小辛庄社区恒协基爱养老服务中心的“长驻客”。每天早饭后，张奶奶便像小孩上学一样，来到养老服务中心，看看电视、打打麻将、跟一帮老姐妹唠唠嗑，中午花3块钱吃一顿三菜一汤的午餐，睡个午觉，下午四五点钟准时回家。张奶奶高兴地告诉记者：“中午三菜一汤的餐标是10元钱，营养搭配均衡，每天不重样。但是我只需要支付3元钱就可以,剩余的费用由居委会和养老服务中心分担。”

2 盾构隧道工程概况

项目主体为珠海市珠机城际轨道交通工程拱北至横琴段隧道，横琴盾构隧道1#井～湾仔北区间全长1.237km，右线全长1.230km，双洞单线，采用盾构法施工。1#井～湾仔北站盾构区间，分别设置半径R=400m、R=800m 及R=500m转弯段，该盾构区间的纵剖面图显示该隧道呈向下走的趋势，最大的坡度为15.7‰，隧道顶板距离地表厚度有6.1～16.5m。

区间隧道穿越地质情况复杂，穿越多种地层，主要有人工填土层、粉质黏土、全风化花岗岩、弱风化花岗岩等，部分地段含有大体积球状风化孤石，给盾构施工带来较多难题（图1）。

图1 盾构区间地层岩性分布图

3 盾构掘进参数预测

3.1 模型输入输出参数选择

本文主要目的是通过已知的地质资料，采用PSO-BP 神经网络对盾构掘进施工参数进行预测，以期指导盾构施工，现将已知的数据资料分为两类，一类是能够反映外部环境变量的输入变量，主要包括岩土体天然重度γ（kN/m3）、土体变形模量E（MPa）、土体黏聚力c（kPa）和内摩擦角φ（°）4 种参数。另一类是能够反映盾构机工作状态的输出变量，主要包括总推进力F（kN）、推进速度v（mm/min）、刀盘扭矩T（kNm）、刀盘转速n（r/min）、土仓压力Pt（MPa）和刀盘贯入度a（mm/r）6 种参数。当掘进断面含有2 种及以上复合地层时，输入变量的选取要根据各地层所占掘进断面面积的比例计算其加权平均值[10]。

由于各掘进参数的量纲不同，且各参数数量级相差较大，如果直接进行网络训练，会导致网络收敛速度慢、预测精度低等问题，因此需要对掘进参数进行归一化处理，本文采用的归一化处理公式为

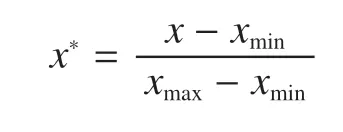
式中x——实际值；

xmin——实际值中的最小值；

xmax——实际值中的最大值；

x*——归一化值。

3.2 PSO-BP神经网络模型建立

在使用粒子群优化算法对BP 神经网络进行优化之前，首先需要确定BP 神经网络的网络结构。BP 神经网络算法结构中包含一个输入层、多个隐含层、一个输出层，及各层之间的连接权值与神经元阈值。理论上，隐含层数目越多，训练出来的网络预测误差越小，但与此同时带来的问题是网络训练时间的延长和网络训练容易陷入局部最优解，不能够寻找全局最优解，而且采用多隐含层还会导致训练过程中放大噪声的不利影响，使网络不能够快速收敛。理论研究已经证明，具有至少一个S 型隐含层加上一个线性输出层的网络，可以逼近任何有理函数。由于掘进参数是一个随时间连续变化的量，而且单隐含层已经能够完全满足预测精度，所以本文采用具有单隐含层的3 层BP 神经网络结构。

在BP 神经网络结构中，各层的节点数选择对网络训练过程和结果有着重要的影响。其中，输入层和输出层节点数的确定跟实际问题相关，本文中的输入量有岩土体天然重度、土体变形模量、土体黏聚力和内摩擦角，所以输入层节点数设置为4；输出量有总推进力、推进速度、刀盘扭矩、刀盘转速、土仓压力和刀盘贯入度，所以输出层节点数设置为6。

确定隐含层节点的数目较为困难，目前，主要有几种经验公式来确定隐含层节点数，采用较多的是由Hhcht Nielsen 提出的经验公式[11]：n=2a+1，本文采用该经验公式来确定隐含层神经元节点数。其中a=4，故n=9。因此，设置的BP神经网络的结构为4-9-6。

在确定BP 神经网络结构后，需要实现粒子群算法和BP 神经网络的结合。基本思想是将BP神经网络的连接权值与阈值转化为粒子群算法中的各个粒子，建立起连接权值与阈值和各个粒子间的映射关系，即用各粒子的位置向量来代替，然后通过粒子群算法不断迭代，得到最优种群的粒子，此时，该粒子的位置向量值可以转化为BP 神经网络全局最优连接权值和阈值，从而建立PSO-BP 神经网络算法模型[12～13]。

3.3 实际工程掘进参数预测

建立PSO-BP 神经网络模型的初衷就是能够根据已知的地质参数预测出后续盾构掘进参数的适宜值，因此，我们对上节训练完成后的PSOBP 神经网络模型输入横～四区间60 环已知地质参数，来预测该60 环盾构掘进参数，以此来检验所建立的预测模型的预测精度和推广泛化能力。

绘制预测值与原始值的对比曲线如下图2～图7 所示。可以看出所建立的PSO-BP 神经网络模型能够较好的预测后续盾构掘进参数，为了评价网络模型的预测精度，需要分析预测的60 环掘进参数原始值和预测值的相对误差和平均误差，通过计算预测样本原始值与预测值相对误差可知，建立的模型对盾构掘进参数的预测有良好的效果，各参数的平均误差均在10%以内，其中最小平均误差为刀盘转速2.06%，最大平均误差为贯入度8.83%，可以看出预测模型具有较好的网络泛化推广能力和预测精度，可以为后续复合地层盾构掘进施工提供掘进参数的预测，具有一定的指导作用。

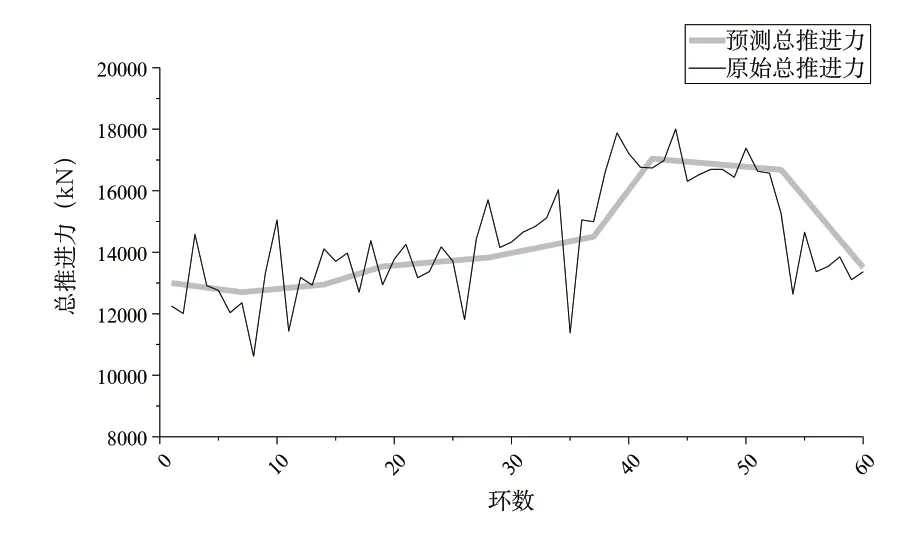
图2 总推进力原始值与预测值对比

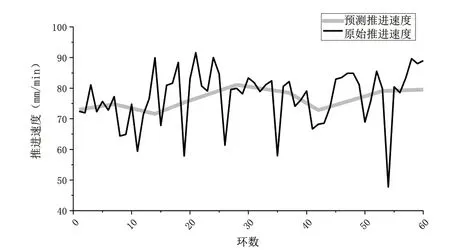
图3 推进速度原始值与预测值对比

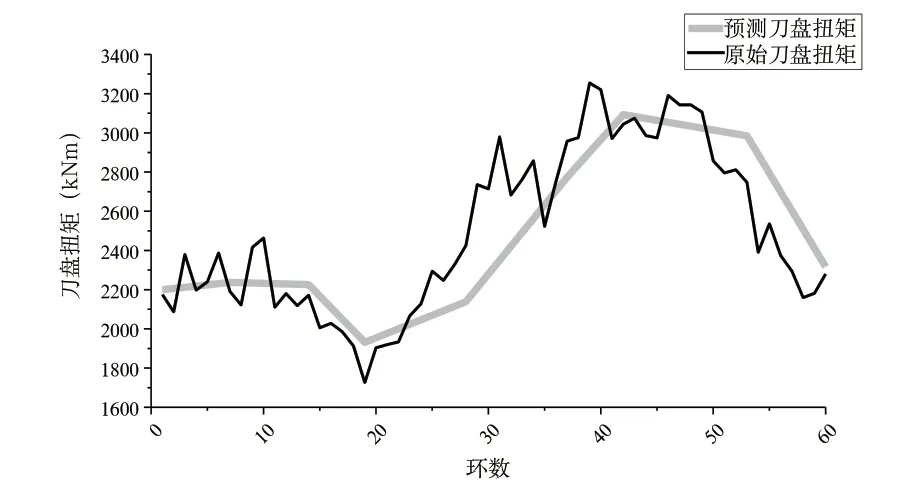
图4 刀盘扭矩原始值与预测值对比

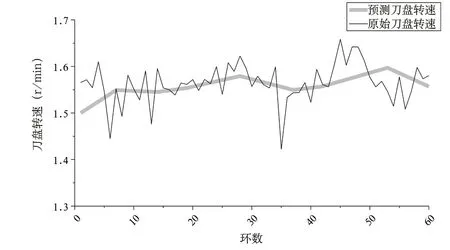
图5 刀盘转速原始值与预测值对比

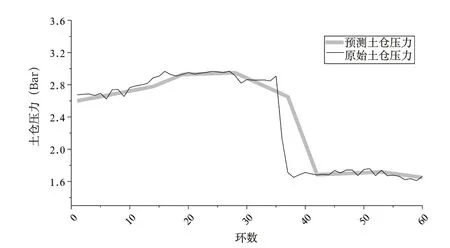
图6 土仓压力原始值与预测值对比

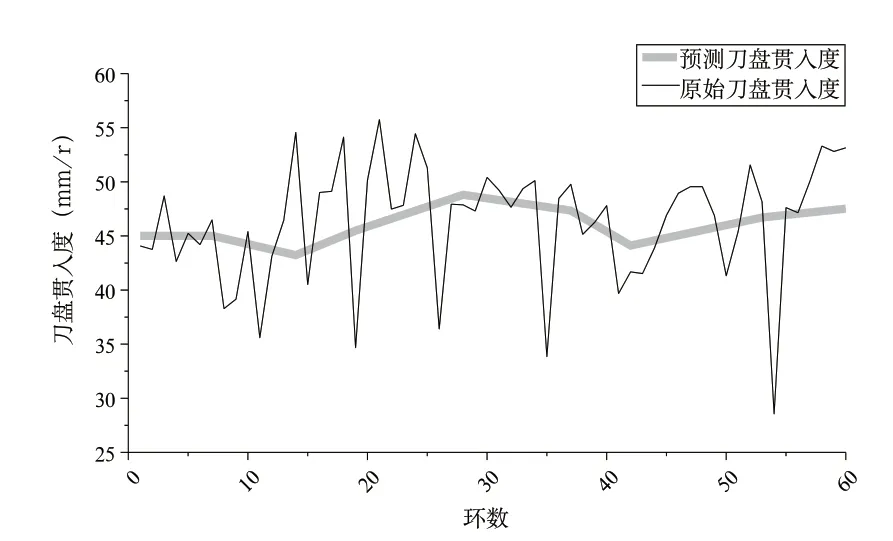
图7 刀盘贯入度原始值与预测值对比

4 结论

1）所建立的PSO-BP 神经网络模型在完成训练后，掘进参数预测值的变化规律能够和实际值基本保持一致，但由于实际工程施工中，盾构掘进参数存在小范围波动性，因此预测值不可能和实际值完全保持一致。因此，将地质参数作为输入变量后，所建立的PSO-BP 神经网络模型能够较为完整的还原实际盾构掘进参数的变化规律，并且产生的预测值大小和实际值误差也在允许的范围内，可以认为建立的掘进参数预测模型对样本数据的学习训练结果能够满足要求。

2）分析预测样本原始值与预测值相对误差可知，建立的模型对盾构掘进参数的预测有良好的效果，各参数的平均误差均在10%以内，其中最小平均误差为刀盘转速2.06%，最大平均误差为贯入度8.83%，可以看出预测模型具有较好的网络泛化推广能力和预测精度，可以为后续复合地层盾构掘进施工提供掘进参数的预测。

3）所建立的PSO-BP 神经网络模型结构简单，具有较好的网络推广泛化能力，并且将地质条件数据作为输入参数，数据方便收集，模型预测精度和预测范围能够满足现场施工要求，为珠海等具有复合地层的地区提供了一种简便有效的方法，从而对盾构掘进参数进行良好的预测，对实际工程施工有一定指导作用。