适应拓扑变化的拥塞最小化网络更新策略

吕娜，陈坤,*，陈柯帆，朱海峰，潘武

1. 空军工程大学 信息与导航学院，西安 710077 2. 中国人民解放军94860部队，南京 210000

伴随着战争形态向信息化、网络化和智能化的演变，为提升航空作战平台效能发挥，航空集群作战的概念被提出。由一定数量、能力各异的有人/无人航空平台组成航空集群，以网络为中心，根据作战需求进行灵活高效的组织协同，从而实现平台间优势互补，最大限度提升作战效能[1]。

机载网络作为各航空集群成员信息传输、共享的承载，是进行高效协同作战的核心前提。而当下以各类数据链为代表的机载网络依然采用传统的分布式网络体系架构，网络的维护和管理复杂僵化[2]。与内部协议紧耦合的网络设备，只能根据所需网络服务添加越来越多的协议，难以升级和拓展功能，严重制约了机载网络的作战效能发挥。

软件定义网络(Software-Defined Networking, SDN)为航空集群机载网络的发展打开了新局面[3]。SDN将控制功能从网络设备中独立出来，采用逻辑集中的控制器进行统一监视与管控，控制平面与数据平面的解耦使得对网络的集中管控和资源的灵活调度变得更加简单[4-6]。文献[7]将SDN范式与机载网络相融合，提出软件定义航空集群机载网络(Software-Defined Airborne Network of Aviation Swarm, SDAN-AS)，但机载网络引入SDN带来诸多好处的同时也为网络的一致性更新带来了一系列新的挑战。

在SDN中，为了响应流量需求变化、链路或节点故障、安全策略变化等事件，需要频繁地更新网络状态[8]。而网络状态的更新依赖于对交换机转发规则的更改，需要在一系列交换机上添加、删除或修改流表规则。尽管SDN提供了逻辑集中的控制，但本质上依然是复杂的异步分布式系统[9]。由于控制器与交换机之间存在固有的不可预测的延迟，且交换机反应和处理时间存在差异，即使控制器同时下发所有的更改指令，更改指令到达各交换机的时间不同，各交换机成功更改转发规则的时间也不同[10]。这将导致网络更新期间可能出现交换机转发规则不一致，继而产生如转发循环、路由黑洞、链路拥塞等问题，从而影响业务传输的有效性和可靠性，严重降低网络性能[10-12]。因此，网络更新成为亟待解决的挑战性问题，即如何在满足网络一致性的情况下，将初始网络状态转变为最终网络状态。

近年来，研究人员针对各种不同的一致性要求对网络更新问题开展了大量研究。针对无环一致性，文献[13]提出依赖林算法，文献[14]提出反向更新算法，保证了更新期间数据包传输无环路。文献[9]针对数据包一致性提出两阶段更新机制，保证在网络更新期间每个数据包只单一按照旧的路径或者按照新的路径转发，而不是两者的混合。而后,文献[15]提出增量两阶段更新，将更新过程划分为多个轮次，牺牲更新时间来换取流表规则开销的减少。上述2种更新策略只能保证网络更新期间数据包的一致性，无法满足拥塞一致性，即在网络更新期间不产生拥塞。

为实现无拥塞网络更新，文献[16]提出了SWAN(Software-driven WAN)更新系统，为网络中每条链路预留空闲容量s，通过线性规划求解一系列中间状态，并证明了至多需要1/s-1次更新即可实现无拥塞网络更新。但SWAN必须始终预留一部分链路容量，牺牲了网络带宽资源利用率。文献[17]拓展了SWAN中的线性规划公式，提出拥塞最小化(Congestion-Minimizing，CM)更新算法，采用随机舍入法近似计算出给定最大瞬时拥塞情况下的最小化中间阶段数目的更新，用一定的拥塞换取更新速度的提高。文献[10] 提出Dionysus更新系统，构建全局依赖关系图并根据交换机间的依赖关系进行动态更新，从而提高网络更新速度。文献[18]提出Cupid更新系统，通过关键节点将全局依赖图转化为具有潜在拥塞链路的局部依赖图，有效加快更新速度。

上述网络更新策略[10,16-18]能够较好地保证网络更新期间的拥塞一致性，但这些策略主要关注于地面有线网络，网络拓扑是固定不变的，未针对无线网络的特点进行考虑。然而航空集群作战场景下的网络拓扑随着作战任务和需求的变化而变化。拓扑变化必然导致部分旧转发路径失效，继续在其上传输业务时将产生严重的数据包丢失现象[19]，现有的网络更新策略不能适应SDAN-AS的需求。本文针对上述问题，提出适应拓扑变化的拥塞最小化更新策略(Congestion-Minimizing for Topological Changes，CM-TC)，考虑拓扑变化的影响，对受影响的业务流采用重路由机制进行处理，并设计贪婪流迁移算法降低产生的网络拥塞，最后通过拥塞最小化更新算法完成整个网络更新。

1 问题描述

1.1 网络模型

在问题描述之前，首先引入本文的网络模型。本文将软件定义航空集群机载网络抽象为无向图G=(V,E)。其中V={v1,v2,…,vm}表示网络中交换机的集合，E={e1,e2,…,en}表示链路集合。对于∀e∈E，Ce表示该链路的容量。μ={μe1,μe2,…,μen}表示网络链路利用率的集合。Go表示初始网络状态，Gn表示最终网络状态。F={f1,f2,…,fk}表示网络中业务流的集合，对于∀f∈F，df表示该流的需求，将每条流分别打上不同的VLAN(Virtual Local Area Network)标签将流拆分到多条路径进行传输。Po(f)表示Go中的流f的路径集合，Pn(f)表示Gn中流f的路径集合，Pa(f)⊂Po(f)表示Go中流f已失效路径的集合，Fa表示受失效路径影响的流的集合。

1.2 网络更新问题描述

在SDAN-AS场景中，由于作战任务、作战需求的变化，网络拓扑在较长的时间跨度上呈现出较大的变化，但在较短的时间跨度上，网络拓扑的变化可以视为局部的、小范围的变化。网络拓扑的变化可以是由于节点/链路故障或节点间相对运动所导致的。如图1(a)所示，对于源节点为1，目的节点为4的流f，通过打上不同的VLAN标签将流f拆分到多条路径进行传输，流f的路径集合为Po(f)={p1,p2,p3}，p1、p2、p3为图1(a)中实线箭头所指路径。每条路径上的节点根据标签进行相应的转发，在源节点1处为每条路径分配权重实现流量分配。

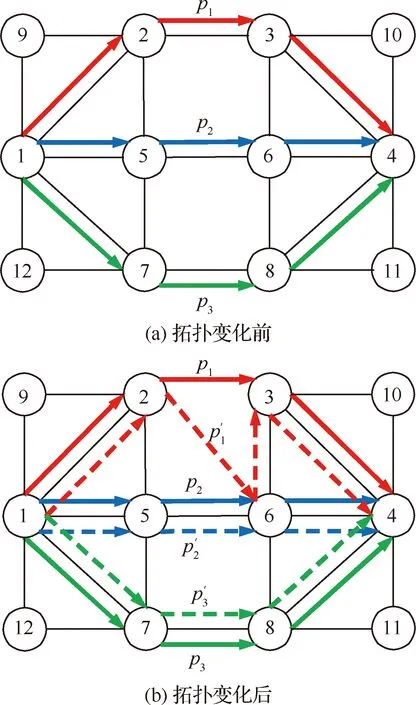
图1 拓扑变化前后的网络状态Fig.1 Network state before and after topology change

当网络拓扑由图1(a)转变为图1(b)时，节点2和节点3之间的链路中断，路径集合中的p1已经失效，然而节点1～节点4交换机中的转发规则没有更改，流f依旧按照p1路径进行传输，节点2 在接收到来自节点1的数据包后，依旧会按照旧的转发规则将数据包向节点3转发，链路e(2,3)的中断将导致数据包无法到达节点3，从而导致p1路径上的数据包无法到达目的节点4，造成严重的数据包丢失。此时，在流量工程周期内，控制器将会根据当前网络拓扑及流量需求计算出全网新的最优转发路径，如图1(b)中的虚线所示，计算出的新转发路径集合为Pn(f)={p′1,p′2,p′3}，p′1、p′2、p′3为图1(b)中虚线箭头所指路径。图1(b)中的实线部分构成初始网络状态Go，虚线部分构成最终网络状态Gn。

网络更新就是将网络状态从Go转换到Gn的中间过程，即将流量从Go中的旧转发路径Po(f)迁移到Gn中的新转发路径Pn(f)上的中间过程[20]。

2 更新策略

为解决由于网络拓扑变化导致的初始网络状态中部分可用路径失效的问题，本文基于CM算法提出CM-TC更新策略。本节首先描述CM-TC更新策略的流程，再对策略中的相关算法进行详细介绍。

2.1 CM-TC更新策略描述

CM-TC更新策略流程如图2所示。

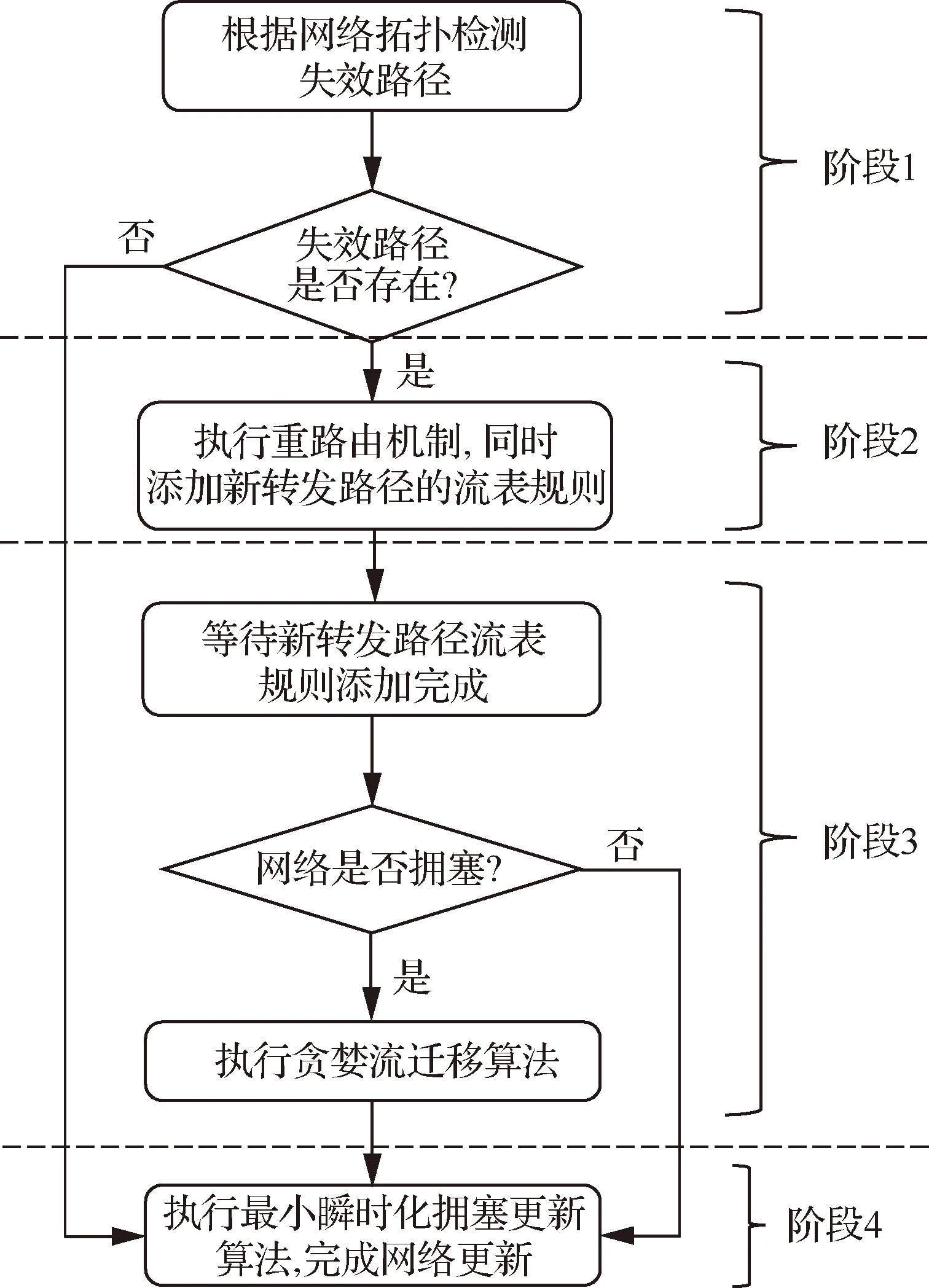
图2 CM-TC更新策略流程Fig.2 Process of CM-TC update strategy

阶段1控制器根据收集到的当前网络拓扑信息，检测失效路径集合Pa，以及受失效路径影响的流集合Fa。若失效路径存在，则执行阶段2，若无失效路径，则执行阶段4。

阶段2将每条受失效路径影响的流f*∈Fa重路由到未失效的路径集合Po(f*)-Pa(f*)上，控制器执行重路由机制计算未失效路径上的流量分配，下发指令修改入口交换机流表中的路径流量分配权重xf,p。同时在网络中添加每条流的新转发路径的流表规则，删除失效路径的流表规则。

阶段3在新转发路径的流表规则添加成功之后，若网络中存在拥塞，则执行贪婪流迁移算法，具体算法细节将在2.2节进行详细阐述。

阶段4执行最小化瞬时拥塞更新算法，通过线性规划计算出给定数目的中间网络状态，将网络从初始网络状态逐个转变为最终状态Gn，完成网络更新。

控制器周期性地执行网络更新策略，首先执行阶段1进行失效路径检测，当检测到旧转发路径中存在部分路径失效时，即按照策略阶段顺序执行。若无路径失效，即无需执行阶段1和阶段2，直接执行阶段4的最小化瞬时拥塞更新算法。

2.2 算法描述

本节配合图3和图4对CM-TC更新策略中的相应算法进行描述。

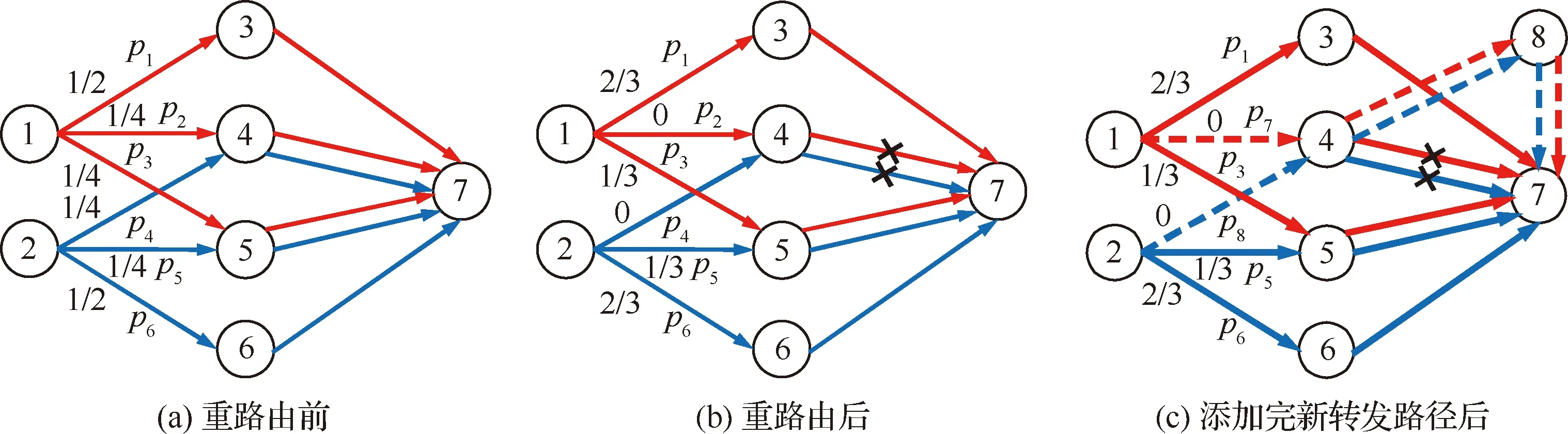
图3 阶段2中的网络状态Fig.3 Network state in the second stage

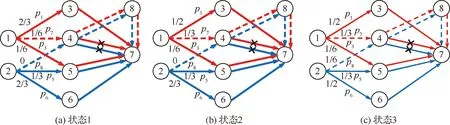
图4 阶段3中的网络状态Fig.4 Network state in the third stage

2.2.1 重路由机制

当旧转发路径中存在失效路径时，更新策略进入阶段2。此时新转发路径的流表规则还没有添加，由于每条业务流新转发路径的流表规则添加需要在该路径上的所有交换机上添加新的流表规则，同时受影响的流数目较多，因此流表规则的添加需要一定时间，在该段时间内网络只能按照旧转发路径传输。考虑到继续在失效路径上传输业务会导致严重的数据包丢失，首先要将受影响的流在失效路径上的流量转移到未失效路径上，即使这可能产生一定的拥塞，但仍优于在失效路径上继续传输带来的直接数据包丢失。同时为了尽可能地减少拥塞，从全局出发重新计算受影响的流在未失效路径上的流量分配权重，从而最大限度地最小化网络最大链路拥塞。因此，问题形式化为

s.t.

(1)

线性规划式(1)的目标函数，即最小化网络最大链路利用率。约束条件第1条表示网络流量需求守恒；第2条表示受路径失效影响的流f∈Fa在失效路径p∈Pa(f)上的权重为0，其中xf,p表示重路由后流f分配到路径p上的流量权重。第3条表示流的多路径路由约束，由于重路由机制只将受影响流在失效路径上的流量进行重路由，未失效路径上的并不变动，因此受影响流重路由之后的流量分配权重将大于等于其旧的网络状态中的流量分配权重，其中xf,p表示旧的网络状态中的流f分配到路径p上的流量权重；第4条表示未受影响的流的流量分配权重保持不变。通过标准线性规划求解器对线性规划式(1)进行求解即可计算出重路由之后转发路径上的流量分配，即重路由之后的网络配置。

如图3(a)中，每条链路的容量为1，节点1～节点7的流f1通过红色的3条路径进行传输，节点2～节点7的业务流f2通过蓝色的3条路径进行传输。2条业务流的需求都为2，路径上的流量划分见图中标注。当节点4～节点7之间的链路故障时，检测到p2和p4这2条路径失效后，执行重路由机制，将其上的流量重路由到未失效的其他路径上，通过线性规划计算出的流量划分如图3(b) 所示。在图3(c)中，虚线表示的p7和p8为添加的新路径，p2和p4这2条失效路径已被删除。

2.2.2 贪婪流迁移算法

在执行完重路由机制且新转发路径的流表规则已添加成功后，更新策略进入阶段3。尽管阶段2中的重路由机制减少了数据包的直接丢失，但可能会使网络产生一定程度的拥塞。CM算法利用短暂的网络瞬时拥塞换取网络更新时间的减少，在更新期间会产生瞬时拥塞，而执行完重路由机制后的网络是存在一定拥塞的，若直接执行CM算法将网络转变到最终网络状态，难以达到CM算法原有的效果，与CM算法在常规网络更新中达到的效果相比，将会在网络更新期间产生更大程度的拥塞。因此需要在执行CM算法之前尽可能地通过流量迁移降低网络拥塞。

针对重路由机制带来的网络拥塞问题，在阶段3中设计贪婪流迁移算法以降低网络拥塞程度，如算法1所示。首先找出链路利用率最大的链路e*，若该链路存在拥塞，则将经过该链路的所有业务流添加到集合F*中；然后对于集合F*中的每一条业务流f，计算其转发路径中的剩余容量Cr(f,p)；之后找出剩余容量最大的流f*以及对应的剩余容量最大的路径p*；再将流f*经过链路e*的路径上的流量迁移到具有最大剩余容量的路径p*上；循环上述过程，直至控制器检测到网络无拥塞或无法找到具有剩余容量的路径时终止算法。

对应图3(c)中，首先找出拥塞最大的链路e(5,7)，经过该链路的流为f1和f2，剩余容量Cr(f1,p7)=Cr(f2,p8)=1，因此任选其一进行迁移即可。选择将f1在p3上的流量部分迁移到p7上，流量划分如图4(a)所示。然后找出图4(a)中拥塞最大的链路e(3,7)，经过该链路的流为f1，剩余容量Cr(f1,p7)=2/3，因此将f1在p1上的部分流量迁移到p7上，流量划分如图4(b)所示。再找出图4(b)中拥塞最大的链路e(6,7)，经过该链路的流为f2，剩余容量Cr(f2,p8)=1/3，因此将f2在p6上的部分流量迁移到p8上，流量划分如图4(c)所示。此时网络无拥塞，算法终止。

算法1:贪婪流迁移算法输入:链路集合E;流集合F;链路容量C;路径集合P;流需求集合df;当前网络配置xf,p;链路利用率集合μ输出:贪婪流迁移后的网络流量配置xf,p1. Whileμmax>1do;网络存在拥塞开始循环2. F*=Φ, Cr=Φ, e* = argmax (μ)进行变量初始化3. for eachf∈Fdo4. if 流f的转发路径p经过链路e*then5. 将流f添加到集合F*中6. 标记流f经过e*的路径pc(f)=p7. end if8. end for9. for eachf∈F*do10. for eachp∈P(f)do11. if∀e∈p都满足μe<1then12. 计算流f在路径p上的剩余容量Cr(f,p)13. end if14. end for15. end for16. ifCr==Φthen17. break18. end if19. (f*,p*)=argmax Cr(f,p) ;找出空闲容量最大的流f*以及对应的路径p*20. T=min(df*·(xf*,pc(f*)-1),Cr(f*,p*));计算待迁移的流量值T21. xf*,p*=xf*,p*+T/df*;增加流f*在路径p*上的流量权重22. xf*,pc(f*)=xf*,pc(f*)-T/df*;减少流f*在路径pc(f*)上的流量权重23. 执行算法1更新集合μ24. end while

贪婪流迁移算法每次对拥塞最大的链路上的流量进行迁移，贪婪地占用具有最大剩余容量的路径，从而减少迁移次数，在较短的时间内尽可能地降低拥塞流的数目、降低最大链路拥塞。拥塞流迁移的实现，通过控制器向该流的入口交换机下发指令修改流表中转发路径上流量分配权重完成。

算法1第1行表示，当网络最大链路利用率μmax>1时开始循环；第2行进行变量初始化和赋值，其中，e*表示网络链路利用率最大的链路，F*表示经过链路e*的流的集合，Cr表示剩余容量。第3～8行将经过拥塞最高的链路e*的流f加入到集合F*中，并标记出每条流f∈F*经过链路e*的路径pc(f)=p；第9～15行计算出每一条流f∈F*的每一条路径p∈P(f)的剩余容量Cr(f,p)；第16～18行表示，若任何一条流的任何一条路径都没有剩余容量则终止算法；第19行找出剩余容量最大的流f*及其对应的路径p*；第20～22行将流f*在拥塞路径pc(f*)上的流量部分迁移到存在剩余容量的路径p*上；第23行执行算法1更新链路利用率集合μ；之后进行循环，直至μmax<1或在经过e*的流中无法找到存在剩余容量的路径，则结束算法循环。

2.2.3 最小化瞬时拥塞更新算法

在更新策略进入阶段4之后，网络拥塞已经得到较好的缓解，此时采用最小化瞬时拥塞更新算法，计算出给定数目中间状态的网络配置。

假设给定网络更新期间中间状态数目为n，则网络状态集合为S={S0,S1,…,Sn+1}，其中S0表示初始网络状态，Sn+1表示最终网络状态，Si(i∈{1,2,…,n})表示第i个中间状态，Si→Si+1表示网络从第i个状态转变为第i+1个状态的更新过程。

定义1最小化瞬时拥塞更新

已知S0和Sn+1状态下的网络配置，计算n个中间状态的网络配置，从而最小化网络更新期间的瞬时拥塞。

定义2瞬时拥塞

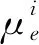
(2)

因此最小化瞬时拥塞更新算法可以形式化为

(3)

线性规划式(3)的目标函数，即最小化网络最大瞬时链路利用率。约束条件的第1条表示在任意的Si→Si+1期间，任意链路e在最严重的情况下的拥塞程度不超过μ，即链路e上待减少的流量还没有减少，但待增加的流量已经增加了；第2条表示网络流量需求守恒；第3条表示受路径失效影响的流f∈Fa在失效路径p∈Pa(f)上的权重为0，约束第4条表示流的多路径路由约束。通过求解线性规划式(2)即可计算出最小化网络拥塞更新期间n个中间状态对应的网络配置。

3 仿真结果及分析

本文的仿真实验运行在CPU为Intel Xeon，主频为3.2 GHz，内存16 GB的商用服务器上。本文采用的仿真软件为Exata 5.1网络仿真软件。EXata是针对新型无线通信技术而设计的半实物网络仿真平台，精确程度与真实网络相媲美，采用先进的并行算法，能够仿真上千个节点的大型无线网络，特别适合集群式计算系统的复杂仿真项目。本节基于EXata网络仿真平台对本文提出的CM-TC网络更新策略进行仿真分析。同时与One Shot、SWAN、CM等网络更新算法进行比较，从而验证分析其性能。

3.1 仿真参数设置

仿真参数设置如表1所示。在仿真区域内随机生成网络节点，仿真场景区域根据航空集群作战范围设定为1 000 km×1 000 km，节点数目由小规模到大规模集群在20～100范围内变化，根据节点通信半径生成网络拓扑图，节点通信半径为当前航空数据链系统的稳定传输距离200 km每个节点随机移动，节点移动速率按照作战飞机巡航速度从低速到高速在200～1 200 km·h-1的范围内变化。然后在节点间随机生成业务流，其需求服从均值为5、方差为1的正态分布。控制器根据全网视图从全局出发为每条业务流计算出多条边不相交的路径，将每条业务流拆分到多条路径进行传输，通过线性规划计算流量划分，并将转发规则下发到每个节点，节点根据转发规则进行流量转发、处理。而后在每一个流量工程周期内根据当前网络拓扑重新计算新转发路径，执行网络更新策略。

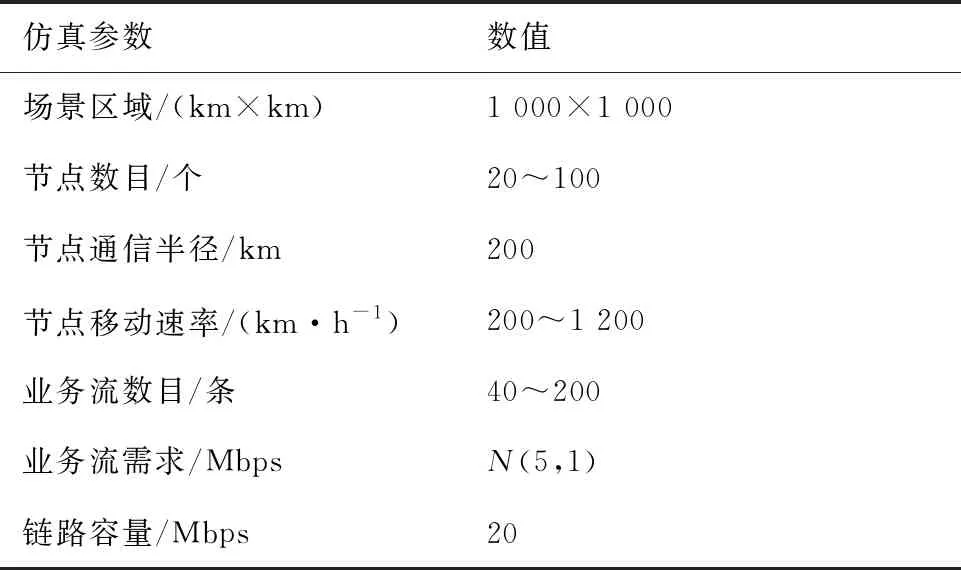
表1 仿真参数设置Table 1 Simulation parameter setting

仿真选择对比的算法描述如下：

1) SWAN。该算法为无拥塞更新算法，将初始网络状态和最终网络状态作为输入，通过线性规划，计算出一系列的中间状态，从而实现无拥塞网络更新。由于该算法需要为每条链路预留一定的带宽，不会产生拥塞，在本场景中只进行流表规则数目和丢失数据包数目的比较。

2) One Shot。该算法是指直接由控制器向网络中的所有交换机节点下发所有的流表，所有交换机同时更新，没有中间状态过渡，直接由初始网络状态更新到最终网络状态。

3) CM。该算法以给定的中间状态数以及网络的初始和最终状态作为输入，通过线性规划，求解出一系列中间网络状态，从而实现给定中间状态数情况下的最小拥塞更新。

3.2 仿真结果分析

图5为网络更新期间丢失数据包数目的比较，可以看出One Shot、SWAN、CM这3种算法的丢包率远远高于CM-TC。由于该场景中网络节点随机移动，网络拓扑动态变化，当网络拓扑发生变化时，初始网络状态中的部分路径将会失效，继续在其上传输业务将会丢失大量数据包。而One Shot、SWAN、CM并没有考虑到网络拓扑的变化，3种算法随着业务流速率的增大将会丢失大量数据包。其中，由于One Shot直接从初始网络状态同时更新所有交换机到最终网络状态，导致网络过度拥塞，因此丢失了大量数据包。CM和SWAN都采用了中间状态进行过渡，CM中拥塞较小、SWAN中无拥塞，但由于需要相对较长的更新时间而导致失效路径上的数据包丢失较多。而CM-TC采用了重路由机制，将受影响的业务流分配到失效路径上的流量，线性规划后重路由到其他的可用路径上，大大减少了更新数据包的丢失。相比于SWAN和CM算法，CM-TC降低了约81.32%的数据包丢失。

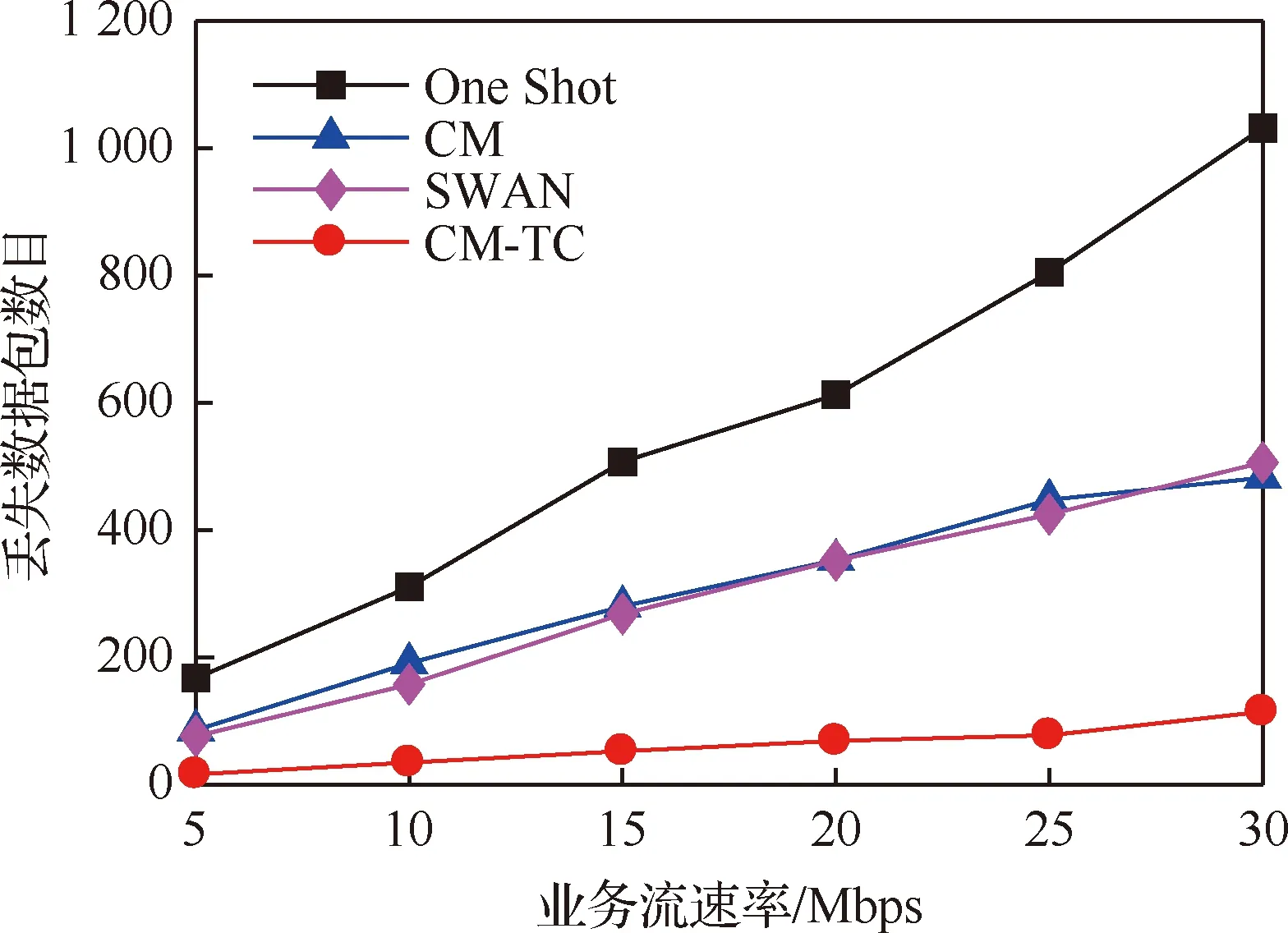
图5 丢失数据包数目比较Fig.5 Comparison of number of lost packets

图6为网络更新过程中拥塞链路的瞬时链路利用率比较，SWAN为无拥塞更新算法，因此这里不做比较。CM算法和CM-TC算法中，设定中间状态数目为3。从仿真结果可以看出，One Shot算法的最大瞬时链路利用率达到了将近200%，正是由于One Shot直接同时更新网络中所有交换机所导致的严重网络拥塞。而CM和CM-TC算法都大大降低了网络更新中出现的瞬时拥塞，最大瞬时链路利用率只有大约130%，与One Shot算法相比，最大瞬时拥塞降低了约30.73%。在实际运行的网络中，对弹性流量和优先级较低的业务流而言，短暂的速率降低或流量拥塞是可以忍受的，因此CM和CM-TC算法带来的瞬时链路拥塞是可以接受的。CM-TC相比于CM算法效果稍稍有所降低，这是由于CM-TC采用的重路由机制在大大减少数据包丢失的情况下也带来了一定的网络拥塞，但两者基本处于同一水平，CM-TC算法在降低网络更新期间的瞬时拥塞方面仍然表现出较好的水平。

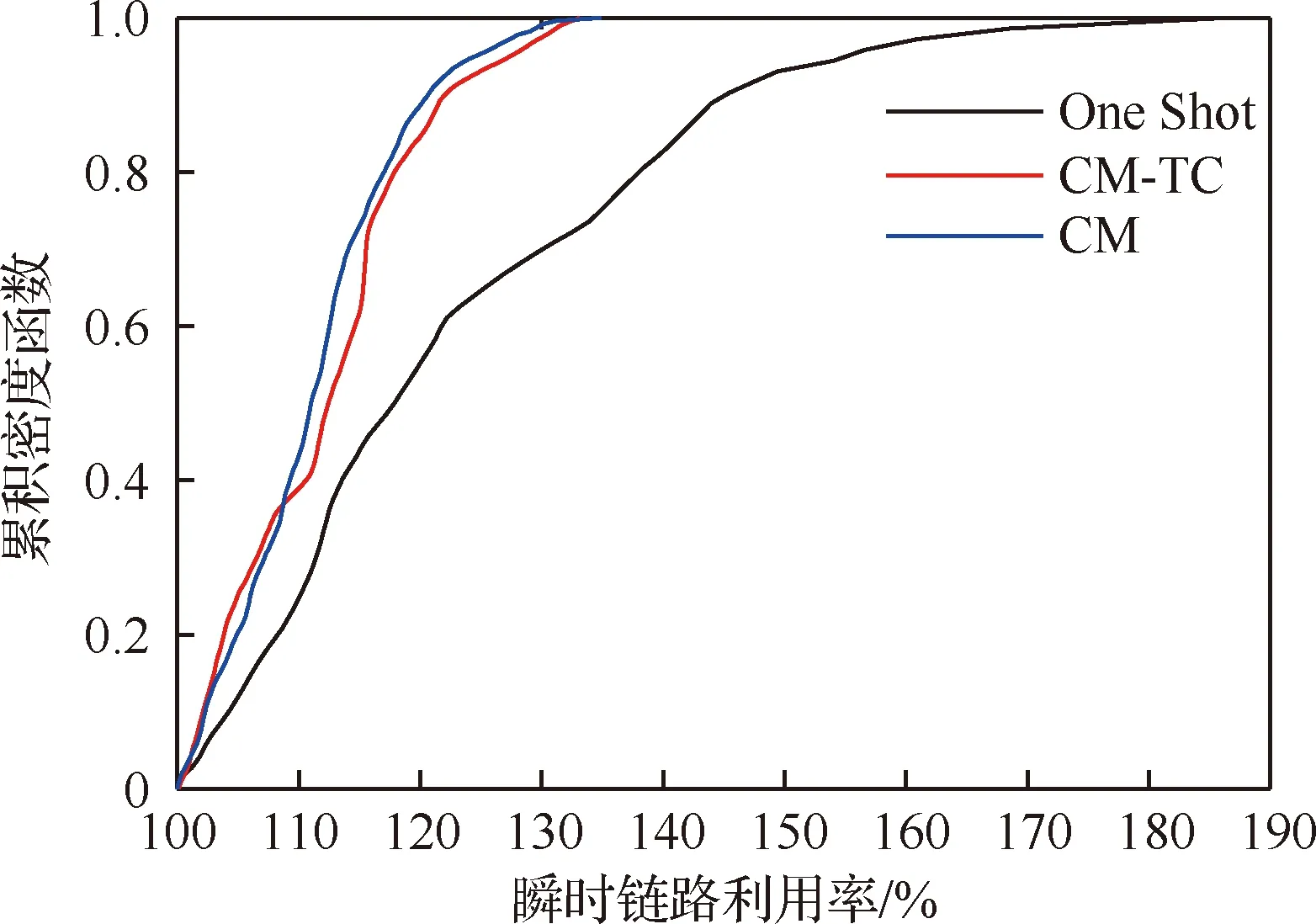
图6 瞬时链路利用率比较Fig.6 Comparison of instantaneous link utilization

图7为网络更新过程中产生拥塞的业务流数目，拥塞业务流的数目随着业务流总数目的增加基本呈现线性增加。由于One Shot算法没有中间过渡状态，同时更新网络中的所有交换机，导致网络中将近85%的业务流产生拥塞。与之相比，CM和CM-TC算法避免了网络更新期间大部分业务流的拥塞，只有接近30%的业务流受到影响。CM-TC相较于CM算法，拥塞业务流数目有所上升，但差距并不明显，说明由重路由机制带来的网络拥塞经过贪婪流迁移算法的处理后有了较大的改善，效果较好。

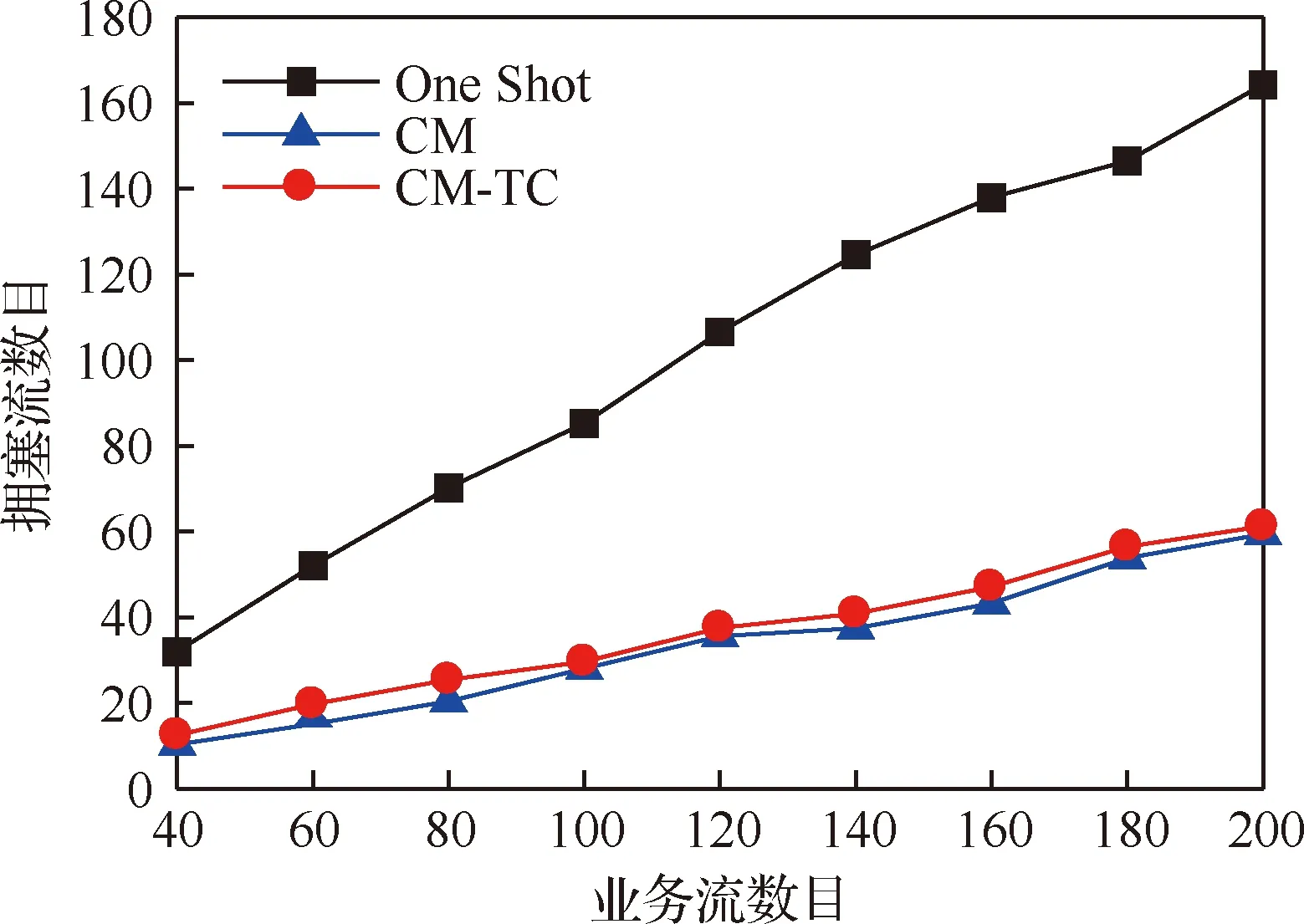
图7 拥塞业务流数目比较Fig.7 Comparison of congested flow numbers

图8为网络更新期间产生的流表规则开销，即添加、修改和删除的流表规则数目。可以看出，One Shot算法对应的流表规则开销最低，SWAN算法对应的流表规则开销远远高于CM与CM-TC。One Shot算法没有中间状态过渡，只需要添加、修改和删除必要的流表，因此具有最低的流表规则开销。与之相反，SWAN算法为了实现无拥塞的更新需要更多数目的中间状态进行过渡，带来了最多的流表规则开销。CM与CM-TC不追求无拥塞更新，旨在实现限定中间状态数目情况下的最小拥塞更新，只需要较少数目的中间状态即可完成网络更新，从而实现了较小的流表规则开销。与SWAN算法相比，CM-TC降低了约41%的流表规则开销；与CM算法相比，仅仅增加了5%左右的流表规则开销。

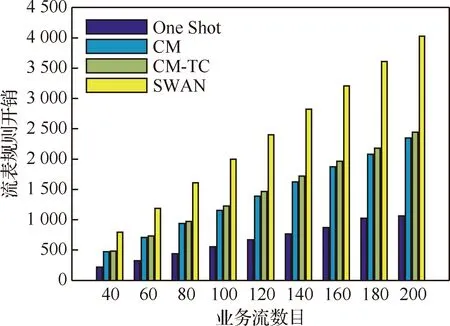
图8 流表规则开销比较Fig.8 Comparison of overhead of rules

根据以上仿真结果，可以看出，CM和CM-TC算法能够有效简化网络更新问题，牺牲较少的网络性能换取更新速度提高的同时，减少了流表规则开销。本文提出的CM-TC算法在网络拓扑动态变化的航空集群场景中，与传统拥塞一致性更新算法相比，显著减少了网络更新期间的数据包丢失。虽然采用了重路由机制可能产生一定的拥塞，但本文进一步设计的贪婪流迁移算法有效降低了网络更新期间的瞬时拥塞，减少了拥塞流数目。与CM算法相比，在规则开销、网络拥塞方面仍然表现较好，同时显著降低了网络更新期间的数据包丢失。

4 结 论

1) 提出的CM-TC算法对拓扑变化进行考虑，在更新之前采用重路由机制进行处理，与其他拥塞一致性更新算法相比，大大降低了丢包率，减少了拓扑变化导致的网络更新期间的严重数据包丢失。

2) 针对重路由机制导致的拥塞上升进一步设计了贪婪流迁移算法，有效地降低了网络更新期间的瞬时拥塞。

3) CM-TC用规则开销、网络拥塞方面的少量提高换取了网络更新期间数据包丢失的显著降低，适应航空集群场景的网络更新需求。