基于ARIMA 模型对社会消费品零售总额的预测分析
——以甘肃省陇南市各县为例
樊 亮
1 问题的提出
社会消费品零售总额是整个零售市场的总规模和总容量,是研究人民生活水平、社会消费品购买力和货币流通等问题的重要指标[1-2].现阶段人民的生活水平在不断地提高,经济增长的重要组成部分之一便是居民的消费需求.近年来,陇南市各县区社会消费品零售总额呈增长趋势,如何运用适当模型对其进行分析,了解居民的消费需求以及陇南市各县区社会消费品零售总额的发展趋势,通过最终模型的预测结果可以使这些问题迎刃而解,以此为基础帮助相关部门作出决策,并进一步提出合理的依据和参考.
2 模型介绍与数据说明
2.1 模型介绍
ARIMA 模型是由三个过程组成的单整自回归移动平均模型:自回归过程(AR(p)),单整(I(d)),移动平均过程(MA(q))[3].在这个模型中,时间序列被认为是一个可用数学模型来描述的随机过程,当此模型可以确定时,则可以利用该时间序列的过去值和现在值预测未来值,该模型反映了时间序列过去与现在[4],未来与现在之间的关系,适用于短期预测.
ARIMA 模型是对非平稳序列经过d阶差分后使其成为平稳序列,ARIMA(p,d,q)模型的具体表达式如下[5]:

其中:Xt为时间序列,B为延迟算子,φi(i=1,2,…,p)为自回归模型系数,θi(i=1,2,…,q)为移动平均模型系数,εt为白噪声过程,p为自回归模型的阶数,q为移动平均模型的阶数.ARIMA 模型建模通常分为四个步骤,即序列的平稳性检验,模型的初步识别,模型的参数估计和模型的诊断分析.
2.2 数据说明
本文所使用的数据来自《陇南2018 发展年鉴》.文中研究所涉及的县市与对应序列情况如表1 所示.

表1 市县对应序列一览表
3 模型分析
3.1 模型的平稳性检验
依据文献[6]中数据,绘制陇南市及各县区社会消费品零售总额数据的时间序列曲线如图1 和图2 所示.

图1 陇南市社会消费品零售总额曲线图

图2 陇南市各县区社会消费品零售总额曲线图
从图1 和图2 可以看出,陇南市及各县区社会消费品总额有明显的增长趋势,判断各序列为非平稳时间序列.
在建立模型之前需要对该时间序列进行平稳化处理.通过Eviews8.0 软件对该时间序列进行ADF 检验,检验结果表明,陇南市及各县区数据的ADF 值分别大于1%、5%、10%的临界值,具体数据如表2 所示,原时间序列{Xt}是一个非平稳时间序列,为了消除原始数据中的异方差性,对原时间序列分别作对数处理,得到新的10 个时间序列{LXt},同时为了使非平稳的时间序列具有平稳性,对{LXt}进行一阶差分后得到{DLXt}.对于经济时间序列而言,差分次数即模型ARIMA(p,d,q)中的参数d,通常只取0,1,2,对{DLXt} 进行单位根检验以获得它们的ADF 值,并判断参数d的阶数.ADF 检验结果表明,所有的ADF 值分别大于不同检验水平下的三个临界值,时间序列{DLXt} 接受原假设,即存在单位根的结论,具体情况如表3 所示.继续对{DLXt} 作差分处理,并对差分后的时间序列{D2LXt} 分别进行ADF 检验,其检验结果显示,ADF 值分别小于1%,5%,10%的三个临界值,二阶差分序列{D2LXt} 拒绝原假设,接受不存在单位根的结论,具体情况如表4 所示,因此该时间序列是二阶单整序列,即模型中的d=2.
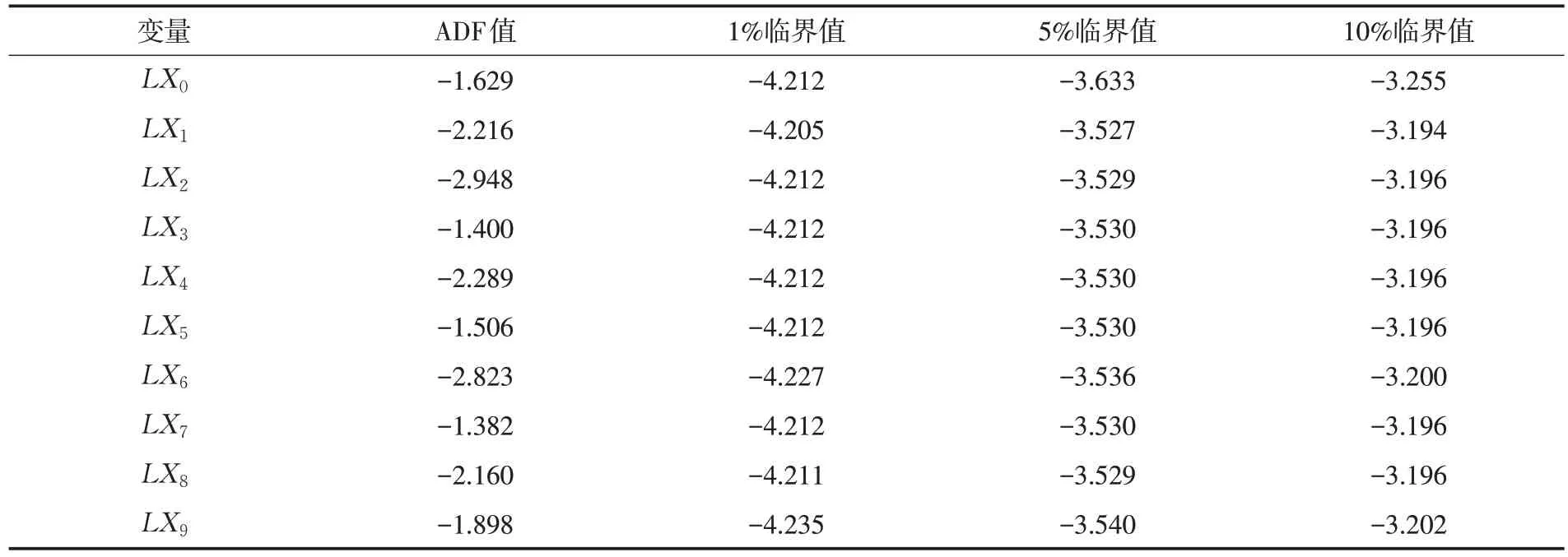
表2 陇南市及各县区时间序列ADF 检验值

表3 陇南市及各县区时间序列一阶差分ADF 检验值

表4 陇南市及各县区时间序列二阶差分ADF 检验值
3.2 模型的识别
依据获取时间序列样本对模型进行形式上的识别,绘制时间序列{D2LXt} 的自相关(AC)图和偏相关(PAC)图,序列 {D2LX0} 的自相关图和偏相关图如图3 所示(t=1,…,9)时的图形趋势和t=0 时一样,不再逐一给出,下同).

图3 序列 {D2LX0} 的AC 图和PAC 图
从图3 可以看出,时间序列{D2LX0} 的相关函数和偏相关函数都是拖尾的,因此判断时间序列组适合于ARIMA(p,d,q)模型.
综上,初步确定模型为ARIMA(1,2,1),ARIMA(1,2,2),ARIMA(2,2,1),ARIMA(2,2,2),运用最佳准则函数定阶法,即AIC 准则法在极大似然值的基础上对模型的阶数和参数给出一组最佳估计.在不同模型的AIC 计算结果中,选取使AIC 最小的那一组阶数为最佳阶数.对于上述的四个模型,通过Eviews8.0 软件得出它们的AIC 值,如表5 所示,分别选取AIC值最小的模型,最终选择模型ARIMA(2,2,2).
3.3 模型参数的估计和诊断
结合表 5 结果绘制模型 ARIMA(2,2)的残差序列折线图与AC 和PAC 图,分别如图4与图5 所示.

表5 各序列初步确定模型比较

图4 模型ARIMA(2,2)残差序列折线图

图 5 模型ARIMA(2,2)残差序列的AC 和PAC 图
从图4 和图5 可以看出,残差序列的自相关函数和偏相关函数均在随机区间内,且图5中最右侧一列的概率值都大于0.05,这说明所有Q值都小于检验水平为0.05 的卡方分布临界值,所选模型的残差序列是一个白噪声过程,最终确定 ARIMA(2,2,2)为最佳预测模型.拟合方程为:

其中各项系数由下面矩阵n的列向量给出.


表6 陇南市各县社会消费品零售总额预测结果及对照
3.4 未来值预测
模型 ARIMA(2,2,2)的残差序列是一个白噪声序列,即满足随机性假设,模型构建合理,可以进行预测.查阅最新的陇南2018 发展年鉴等资料得知,陇南市各县区社会消费品零售总额的最新数据更新到2017 年,运用Eviews8.0 软件的预测功能[7]做出陇南各县区2017 年估计值,并与其实际值进行对照,进一步预测2018 年至2023 年的陇南市各县社会消费品零售总额,具体情况如表6 所示.
4 结语
上述分析表明,运用ARIMA(p,d,q)模型在对陇南市各县社会消费品零售额的预测中,近几年的预测值与真实值之间的误差率较低,但是随着时间跨度的增大,该模型的预测值与实际值之间的误差率逐渐增大,因此,在短期预测中,该模型具有一定的可信度,它从定量的角度反映了陇南各县区经济存在一定的客观问题[8-9],虽然预测结果不能完全代表现实,但是由于其良好的稳定性能,可以此模型为基础,对未来的发展作出预测.从社会消费品零售总额的增长率来看,陇南各县区社会消费品零售总额将保持增长的势头,平均增速为8.16%,考虑到今年的特殊性,虽然年初受突如其来的疫情影响,但是专家表明疫情冲击是短期的,总体是可控的,社会消费品零售增速有望在后半年反弹.总体上看,2020 年陇南各县区的社会消费品零售总额增速缓慢,有个别县出现下滑态势,但陇南市各县区人民生活水平依然有所提高,其消费能力也随消费环境的改变而逐步增强,这都直接带动了社会消费品零售总额的发展.依据预测分析的结果,陇南市政府相关部门可以制定相应的政策,调整和控制宏观经济的整体运作,使得陇南各县区在社会消费品方面的投资占比达到适当水平,促进经济健康发展.

