基于改进SIFT的图像快速自适应匹配算法研究

陶 硕

(马鞍山职业技术学院 电子信息系，安徽 马鞍山 243031)

随着科技飞跃式发展，图像在人们的生活中扮演的角色越来越重要。图像匹配技术是一项利用图像特征来完成不同图像间，相似区域匹配的技术。利用图像匹配技术可以完成当下人们生活中的多个领域的任务。例如：医学检测、安全防卫以及军事侦查等[1-2]。近几年图像匹配技术发展迅速，出现了较多的图像匹配方法，如文献[3]中考虑了图像的尺度特征，在SIFT算法的基础上，利用其提取图像的特征，并采用距离比度量方法实现图像的匹配。文献[4]中利用图像的颜色信息，构成直方图，用于图像的匹配，采用Hessian方法获取图像特征，利用图像特征对应的向量，进行距离测量，将测量结果联合基于颜色信息的直方图进行图像特征匹配。文献[5]中采用Otsu方法获取图像的ROI信息，并采用基于灰度信息的压缩方法，来完成图像间的信息计算，实现图像的配准。为了获取良好的匹配结果，利用向量空间余弦相似性度量距离比度量的匹配方法建立约束条件,保证了良好的匹配点对个数和匹配时间。

可见，经典的SIFT机制在图像匹配领域应用非常广[3-5]。但是，经典的SIFT机制的复杂度较高，其特征向量高达128维，大幅降低了匹配效率[6]，且其对几何内容变换的鲁棒性也不高。因此，本文对SIFT机制予以改进，进一步优化其匹配准确度与效率。最后，测试了所提方法的有效性。

1 SIFT算法基本原理

SIFT算法通过DOG方法从图像中获取其特征[3]。SIFT算法获取的图像特征具有良好的抗干扰性，能够很好的适应尺度等仿射变换。SIFT算法已被广泛应用于目标识别以及影响追踪等多个生活领域[7]。

SIFT通过图像内容上的一些局部兴趣点来获取图像的特征，这个过程与作用在图像上的旋转等变换没有关系，从而促使了SIFT算法的良好抗干扰性能。正由于其良好的鲁棒性能，才能较好的适用多种情景下的应用需求，才能更好地对图像匹配。

1.1 SIFT算法的特点

SIFT的特征是基于图像的兴趣点，具有局部特性。这种特性使得算法获取的图像特征含有大量的信息内容，可以方便的对各类数据进行准确的匹配，同时还能在匹配过程中，提高算法的计算效率。另外，SIFT算法的稳定性能也较好，不仅在图像匹配的各个环节都较为稳定，而且在发生噪声以及亮度变换的情况下，SIFT算法也能较好的保持其稳定性能。SIFT算法经过优化后，计算过程可以得到简化，计算复杂度也可以得到降低，从而提高SIFT算法的效率，因此，SIFT算法还具有较好的拓展性能[7-8]。

得益于SIFT算法的稳定性等多个特性，其可以被较好的应用于多种场景。其中包括亮度变化、旋转变换的图像应用。因此，SIFT算法的适应性较强。SIFT算法实现的过程中，其本质是对图像特征的查找，这些图像特征具有特殊性，不仅能够对图像的关键信息进行描述，而且还能较好的适应多种仿射攻击。在获取图像的特征后，还需要计算出其方向信息等，进而通过一定的方法对图像特征进行匹配[9]。

2 一般SIFT算法简介步骤

2.1 特征点检测步骤

SIFT算法利用高斯核函数G(x,y,β)，从图像中获取兴趣点。二维图像I(x,y)的尺度空间L(x,y,β)可以表示为[10]：

L(x,y,β)=G(x,y,β)*I(x,y)

(1)

式中，β为尺度因子。G(x,y,β)的表述为：

(2)

通过图像空间和尺度空间可以保证局部检测,其过程如下。

D(x,y,β)=[(G(x,y,Jβ)-G(x,y,β))]*I(x,y)

(3)

完成了SIFT特征区域的计算。通过对每个特征点的邻域点的梯度分布特征的位置、规模、方向等可以获得为每个特征点的最重要的信息尺度。

2.2 旋转不变特征点描述

SIFT算法采用关于梯度的直方图方法，计算出图像特征点的方向信息,以确保特征的旋转不变性，通过直方图对每个4×4小窗口的邻域像素的梯度方向进行计数，通过特征向量的归一化消除照明的影响。

2.3 匹配更加准确

可通过欧氏距离相比值的方法实现匹配，如果比值阈值太小，匹配点的数目将大大减少，匹配将更加准确。如果该值太大，则会出现太多无法匹配点。

3 SIFT图像匹配算法的改进

由于SIFT算法在对图像特征进行匹配时，采用的阈值一般是固定值，不能较好的对图像信息进行自适应的变化，导致不同图像的匹配结果差异性较大。为了克服这一弊端，提高SIFT算法的自适应能力，以使得其能够较好的对不同图像或者图像中的不同内容进行适应，本文对SIFT算法采取了以下改进策略：

3.1 使尺度空间的设立、特征点定位与原来算法一样。

3.2 找出特征点，生成特征描述子

例如利用9×9圆形式计算特征点邻域中的12个梯度方向。不同图像的效果是完全不同的。窗口半径为4.5μm，没有自适应性。为了将SIFT算法应用于工业检测，同时使光照保持不变，形成了一个12维特征向量来表示特征点。

3.3 通过自适应匹配找最优化比阈值。

自适应匹配目的就是为了找到最优质的距离比阈值，研究发现，一般图像比阈值T的最优化值小于0.8。对此，本文将阈值初始值设定为0.8，并通过相对指标来评定阈值的调整过程，对该阈值进行自适应的调整，以准确的对该阈值进行设定。改进算法流程为：

构建尺度信息→查找性缺电→计算图像的梯度信息→获取图像特征向量→寻找最大梯↑ →→→适当的减小T←←←↑N度的统计量→初始T为0.8→计算配准率R→相邻2次配准率之差小于定值或者循环次数过大→得出结果→结束

3.4 向量空间余弦相似度匹配

相似函数是表征两个向量之间相似度的函数。余弦相似度是最常见的相似度，反映单个特征的多个分量干扰匹配结果。许多距离度量和相似度函数都是基于两个向量的变形和导出，并度量两个向量之间的相似度。两个矢量之间的差异分别反映在数值和方向特征上。余弦相似性约束被添加到欧氏距离度量，距离测度用于测量空间中矢量的距离。通过设置阈值来减少失配点对的数目。距离越远,向量之间的差异就越大。

3.5 对比RANSAC算法有效消除失配点

向量的最小欧几里得距离与次最小欧几里得距离之比小于0.8，但当外点较多时，其性能将受到很大影响。如果匹配点不正确，则可以通过实验获得经验阈值K。满足这个事实的概率是非常小的，放大和缩小的运动方向大致相同，矢量的长度被归一化。因此,偏离运动方向的匹配点可以被视为失配点。对于2个矢量X和Y，产生大量的失配。其他弦相似度表达式是方向一致的几何约束的比较。在RANSAC算法实现之前，先构造点到方向的匹配直方图，并将点到方向的匹配一致性作为特征点对之间的有效空间几何约束，排除了六对不匹配点，进而得到匹配点对。

综上所述，整个算法的匹配过程见图1。从图1可见，本文算法引入SIFT算法中的高斯核函数法获取图像特征点。利用9×9圆形式计算特征点邻域中12个梯度方向的方法获取特征向量，对SIFT算法中获取图像特征的算法进行改进。采用自适应匹配找最优化比阈值，改进SIFT算法中采用固定阈值的方法，并将最优化比阈值，用于余弦相似度匹配的过程，获取匹配点。采用RANSAC算法消除失配点，获取匹配结果。

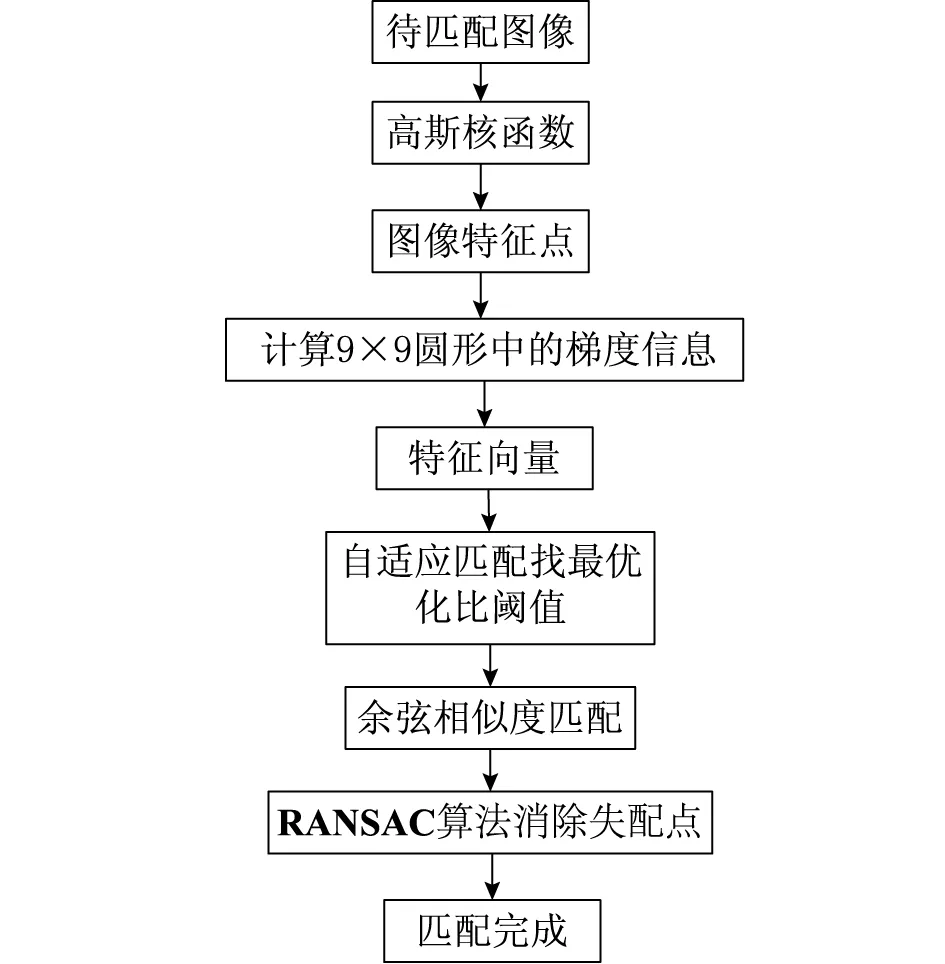
图1 本文算法的匹配过程

4 算法实验与结果分析

实验利用MATLAB7.10软件，在Intel双核处理器、500GB硬盘的戴尔计算机上进行。实验选取文献[11]与文献[12]方法进行对比。

各算法对亮度变化图像的匹配结果及匹配结果对应的数据如图2和表1所示。各算法对旋转变化图像的匹配结果及匹配结果对应的数据如图3和表2所示。

(a)图像A

(b)图像B

(c)文献[11]匹配结果

(d)文献[12]匹配结果

(e)本文算法匹配结果图2 各算法对亮度变化图像的匹配结果

(a)图像A

(b)图像B

(c)文献[11]匹配结果

(d)文献[12]匹配结果

(e)本文算法匹配结果图3 各算法对亮度变化图像的匹配结果

表1 图1中三种算法匹配结果数据

表2 图2中三种算法匹配结果数据

从图2可见，不同算法对亮度变化图像的匹配结果都还好。将各算法的匹配结果进行比较发现，本文改进SIFT算法的匹配结果中的匹配数量最多。从图3可见，不同算法对旋转变化图像都能实现匹配。将各算法的匹配结果进行比较发现，文献[11]算法的匹配结果与文献[12]算法的匹配结果相比本文算法的匹配结果，具有更多的错误匹配点和漏匹配点。从表1和表2也可以发现，本文算法的匹配错误率较低。说明了本文改进SIFT算法具有很好的匹配效果。

结语

本文通过分析SIFT算法的工作原理和特点，指出其不足之处，明确SIFT算法现有缺陷引起的图像匹配弊端。首先，为了克服SIFT算法在图像特征匹配过程中，本文采用了向量空间余弦相似度匹配方法对其进行改进。其次，本文还通过RANSAC算法对匹配后的图像特征进行了计算，将错误匹配点进行删除，获取了更为理想的匹配结果。实验中对亮度及旋转攻击下的图像进行了匹配，验证了本文算法的匹配性能。从匹配结果可以知道，本文算法的匹配效果较好。