基于k密集近邻算法的局部Fisher向量编码方法

冀 治 航， 胡 小 鹏， 杨 博， 田 云 云， 王 凡*

( 1.大连理工大学 计算机科学与技术学院， 辽宁 大连 116024；2.河南科技大学 信息工程学院， 河南 洛阳 471023 )

0 引 言

图像分类一直是计算机视觉研究领域的热点问题．近年来，许多学者致力于图像表达方法的设计和研究，它是图像分类系统中的一个重要环节．迄今为止，多种不同的图像表达模型被相继提出，而目前常用的则是视觉词包模型[1-4]和卷积神经网络[5-7]．近年来，卷积神经网络因其在视觉应用方面的卓越表现而获得了越来越多的关注．但是，该类方法性能的提升往往依赖大规模的数据和算力，且缺乏推理能力，在一定程度上限制了它的应用和部署[8-10]．

此外，视觉词包模型也一直是图像分类任务中常用的图像表达方法之一[1-4]，该模型构建图像表达的过程主要包含以下几个步骤：(1)在训练数据集上随机提取一组图像特征，并利用k-means或高斯混合模型(Gaussian mixture model，GMM)算法构建视觉字典；(2)对图像中的局部特征进行编码并汇集，从而形成图像的表达向量．为了获取具有区分能力的图像表达向量，学者们相继提出了稀疏编码(sparse coding，SC)[11]、局部约束线性编码(locality-constrained linear coding，LLC)[12]、局部聚合描述符向量(vector of locally aggregated descriptors，VLAD)[13]以及Fisher向量(Fisher vector，FV)编码[14]等方法．其中，Fisher向量编码以其优异的性能，得到了很多关注．

然而，在构建Fisher向量的过程中，Fisher向量编码方法要计算每一个局部特征描述符相对于所有高斯子模型似然函数的梯度信息，而忽视了编码的局部性原则[12，15]．该方法不仅削弱了图像表达向量的辨别能力，也增加了计算量．此外，视觉字典中相似子模型的存在即近义词现象，也会给编码结果带来影响[16]．

为了提高Fisher向量编码结果的表达能力，Nakayama[15]提出了基于局部高斯度量(local Gaussian metrics，LGM)的Fisher向量编码改进方法．该方法首先利用k-means对特征空间进行划分，并利用单高斯对每一个聚类区域进行建模，从而构成视觉字典．在编码过程中，LGM会将每一个特征投影到与它邻接的k个高斯子模型上，并分别进行Fisher向量编码，从而形成具有局部特点的Fisher向量图像表达．此外，Garg等[17]将稀疏原则与Fisher向量编码相结合，提出了稀疏判别Fisher向量(sparse discriminative Fisher vectors，SDFV)编码．Lu等[18]同时引入稀疏以及局部性原则，并将它们与Fisher 向量编码相结合，提出了稀疏Fisher向量(sparse Fisher vector，SFV)编码．

近年来，许多学者将卷积神经网络与Fisher向量编码方法相结合，以此构建图像表达．Cimpoi等[19]将CNN预训练模型的最后一个卷积层输出作为图像特征，并利用Fisher向量编码的方式来构建图像表达．Sydorov等[20]借鉴CNN多层构架思想，将Fisher向量编码与SVM分类器的训练过程结合在一起，优化了GMM字典模型的生成过程，提升了分类效果．与原始Fisher向量编码方法相比，上述两个方法分别采用了不同的特征，优化了字典生成过程，但其并未考虑Fisher 向量编码方法中存在的问题．为了区分图像中不同特征之间的重要性，Pan等[21]通过学习方式对不同GMM视觉单词赋予了不同的权重，以此提高了Fisher表达向量的辨别能力．此外，为了使得Fisher向量编码方法能够适应高维CNN特征，Liu等[22]将稀疏表达与Fisher向量编码相结合，提出了稀疏Fisher向量编码．文献[21-22]所提方法是否对传统手工特征也有效，作者并未探讨．Tang等[23]将Fisher向量编码过程进行分解，并融合到卷积神经网络中的多个层中，从而将特征学习与Fisher向量编码的相关参数统一在一起进行端到端的学习，以此获取图像表达．然而该方法需要依赖大规模的数据和算力．

上述这些方法从不同角度对Fisher向量编码方法进行了改进，在一定程度上提升了Fisher 向量的表达能力，但并未考虑高斯子模型间拓扑结构的差异，近义词现象并没有得到解决．为此，本文提出一种改进的Fisher向量编码方法，即基于k密集近邻算法的局部Fisher向量(Fisher vector based onk-dense neighborhood algorithm，KDN-FV)编码．在编码阶段，KDN-FV编码方法会依据高斯子模型间拓扑结构的差异以及编码局部性原则，利用k密集近邻算法[24]为每一个特征描述符筛选编码时所需的高斯子空间．KDN-FV编码方法引入了局部性约束，并且考虑了子空间之间的拓扑结构差异．

1 Fisher向量编码方法

Fisher向量编码方法的设计原理源自Fisher核理论，该理论能够将生成式模型与判别式模型紧密地结合起来．简单地说，Fisher核能够利用一个生成模型的参数信息来定义一个核函数，进而可以构造一个分类器[25]．

假设x={xi；i=1，…，t}是一组观测样本，pλ是由x中样本所构造的生成模型对应的概率密度函数，λ=(λ1λ2…λn)∈Rn，是函数pλ的n维参数向量，则样本x关于pλ似然函数的梯度可定义为

(1)

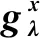
根据信息几何理论，概率分布空间H={pλ}可以形成一个黎曼流形，它在参数λ处的局部度量函数可由Fisher信息矩阵Fλ∈Rn×n给出：

(2)

在Fisher信息矩阵给定的情况下，由样本x和y之间的相似性可以导出Fisher核的定义：

(3)

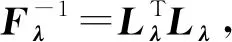
(4)

其中

(5)

式(5)定义的梯度向量为样本x的Fisher向量．

在文献[14]中，Sánchez等将Fisher向量的思想引入到图像编码中．此时样本集x={xi；i=1，…，t}将具体地表示从一幅图像中提取到的局部描述符，例如SIFT、SURF等；而pλ表示含有k个子模型的混合高斯模型，其参数向量λ={wj，μj，Σj；j=1，…，k}，其中wj、μj和Σj分别表示第j个高斯子模型对应的混合权重、均值向量以及协方差矩阵．根据式(5)分别计算出对每一个参数wj、μj以及Σj的梯度，并将其串联起来构成图像的Fisher表达向量．

2 基于k密集近邻算法的局部Fisher向量编码方法

从上述Fisher向量编码方法的介绍中可以看出，该方法在对局部特征描述符进行编码时，会估计每一个局部特征相对于所有高斯子模型的似然函数，并计算相应梯度信息．该方法忽略了编码的局部性原则，削弱了表达向量的区分能力[12，15]．为此，本文提出一种基于k密集近邻算法的局部Fisher向量(KDN-FV)编码方法．该方法能够依据特征空间的分布，以及各个子模型间拓扑结构的异同性，仅选择每一个局部特征的邻近且拓扑结构差异较大的子模型进行编码．

2.1 KDN-FV编码方法的视觉字典构造

与原始Fisher向量编码方法相同，KDN-FV编码方法也采用高斯混合模型方法构建视觉字典．不同的是，改进方法会利用主成分分析法计算每一个高斯子模型中局部特征描述符的主方向向量，并以该向量衡量各个子模型间拓扑结构的差异．具体如图1所示．

2.2 KDN-FV编码方法的理论基础和方法介绍

假设d=(d1d2…dn)是由高斯混合模型方法构成的含有n个单词的视觉字典，集合p={p1，p2，…，pn}中包含了每一个单词对应的最大主成分向量．在KDN-FV编码方法中，将局部描述符到高斯子模型均值向量之间的欧氏距离称为描述符到子模型的距离．同时，任意两个子模型di与dj的主方向向量夹角∠pipj被用来度量两个子模型的拓扑结构差异性，∠pipj越大，差异越大．

定义1对于每一个局部特征描述符，将与其最近邻的m个高斯子模型称为该描述符的候选子模型(candidate sub-model，CM)组．

定义2已知特征描述符f及其候选子模型组c=(df1df2…dfm)，若从中选取的一个含有k(k≤m)个子模型的子集(k-candidate sub-model，KCM)ck能够使得

|ck|=k，ck⊆c

(6)

取得最大值，那么该子集ck被称为有效子模型(valid sub-model，VM)组，记为vm．

这里diff(·)表示ck中两两子模型之间主方向夹角累加和，F(·)表示任意两个高斯子模型间主方向向量夹角的度量函数，定义为

(7)

其中pi为di的主方向向量．

为了克服原始Fisher向量编码方法的不足，在编码阶段，KDN-FV编码方法仅利用每一个描述符邻接的高斯子模型来进行编码，同时需要这些子模型的拓扑结构存在着较大差异．也就是说，KDN-FV编码方法在进行编码时，首先要确定每一个局部描述符的有效子模型组．为此，本文提出了一种构建有效子模型组的方法．

已知一个特征描述符fi及其所对应的候选子模型组ci=(di1di2…dim)，进而可以得到一个m×m的矩阵a，其中aij=F(di，dj)，1≤i，j≤m．假设y是一个m维指示向量，可用来指出ci中的子模型是否属于vmi，即：

(8)

(9)

式(9)是一个k密集近邻求解问题，可由文献[17]中给出的方法求得．

通过求解式(9)，可以获得描述符fi的有效子模型组vmi．此后，对于图像中的每一个描述符fi，KDN-FV编码方法仅用其对应vmi中的高斯子模型进行Fisher向量编码，并将所有描述符的编码结果按照原始Fisher向量编码的方式汇集在一起，由此构成图像的KDN-FV表示向量．

2.3 KDN-FV编码方法的主要步骤

输入：图像I的局部特征描述符集合f=(f1

f2…fl)

视觉字典d=(d1d2…dn)

候选子模型组参数m，有效子模型组参数k

输出：图像I的KDN-FV编码向量kfv

子模块1：计算集合D中每一个描述符的KDN-FV编码

fori=1，2，…，l

步骤1.1利用KNN算法计算描述符fi的候选子模型组ci

indexi←KNN(fi，d，m)

ci←d[indexi]

步骤1.2依据式(7)计算描述符fi所对应的矩阵ai，

foro=1，2，…，m

forq=1，2，…，m

go，gq←ci(o)，ci(q)

%分别提取ci中的第o和第q个元素

aioq←F(di，dj)

%依据式(7)进行计算

end

end

步骤1.3通过求解式(9)，计算描述符fi的指示向量yi

yi←KDN(ai，m，k)

步骤1.4依据向量yi确定fi的有效子模型组vmi

indexi←find(yi) %查找yi中非零元素对应的下标

vmi←ci[indexi]

步骤1.5根据vmi中的每一个子模型，利用式(5)对描述符fi进行Fisher向量编码，从而得到fi的KDN-FV编码kfvi

αi←fit(fi，vmi) %计算描述符fi在有效子模型中各个子空间上分配的权重

kfvi←FV(fi，vmi，αi) %对描述符di进行Fisher向量编码

end

子模块2：将向量kfvi(i=1，2，…，l)进行累加并求平均，得到图像I的KDN-FV编码向量kfv

kfv←sum(kfv1，kfv2，…，kfvl)/l

2.4 基于KDN-FV编码方法的图像分类过程

基于KDN-FV编码方法的图像分类过程的关键步骤如下：

(1)在训练数据集中随机选取一组图像，并从每一幅图像中提取局部特征．

(2)使用GMM方法将所收集的局部特征进行聚类，构建GMM字典．

(3)依次提取数据集中每一幅图像的局部特征，依据已得到的GMM字典，采用2.3节的KDN-FV编码方法对每一幅图像进行编码，从而构建图像表达．

(4)利用训练数据集中图像的表达向量训练SVM分类器．

(5)对新输入的图像进行局部特征提取，然后利用KDN-FV编码方法进行编码并构建图像的表达向量，最后将图像的表达向量输入到分类器中进行判别，从而完成图像分类．

3 实验结果及分析

为了展示KDN-FV编码方法的有效性，分别在15-Scene[26]、Pascal VOC 2007[27]、Caltech 101[28]、Caltech 256[29]以及MIT Indoor 67[30]5个数据集上对其进行验证．图2展示了相关数据集的图像示例．

3.1 实验参数设置

在实验过程中，DenseSIFT描述符以及CNN局部特征被分别用来构建图像表达．所有方法和实验都利用VLFeat[31]、MatConvNet[32]工具包来完成．在DenseSIFT特征提取过程中，每隔4个像素进行一次采样．同时，采用空间金字塔匹配(spatial pyramid matching，SPM)[33]方法，将图像划分为多个规则的矩形区域，这里选择1×1、2×2以及3×1的3层模式．在识别阶段，所有实验都采用SVM线性分类器进行分类识别．

3.2 KDN-FV编码方法关键参数的设置

采用与文献[12，21-22]相同的策略，即采用交叉验证的方式来确定KDN-FV编码方法中参数n、m、k的取值．图3所示为在采用DenseSIFT局部特征的情况下，n、m、k采用不同组合时，KDN-FV编码方法在Pascal VOC 2007数据集上的分类精度．由图所示，当n=256，m=20，k=15时，改进方法能够取得较好的结果．

3.3 基于DenseSIFT特征的KDN-FV图像表达

本节构建基于DenseSIFT特征的KDN-FV图像表达，与经典ScSPM[11]、LLC[13]和FV[14]方法进行比较．此外，为了进一步验证所提方法的有效性，与其他学者提出的局部Fisher向量编码方法进行对比，如LGM[15]、SDFV[17]和SFV[18]．表1列出了相应的比较结果．

表1 基于DenseSIFT特征的KDN-FV图像表达分类性能

在Pascal VOC 2007数据集上，从每类图像中随机抽取200幅进行训练，然后在测试集上进行测试．由表1可以看出，KDN-FV编码方法取得了64.6%的分类精度(n=256，m=20，k=15)，比ScSPM和LLC分别高出12.7%、7.0%；比原始Fisher向量编码方法(FV)高出2.8%．与具有相似思路的改进方法相比，如SDFV、SFV，KDN-FV编码方法依然有明显优势．

在Caltech 101数据集上，从每种类别中随机选取30幅图像进行训练，剩余图像用于测试．同时，相关参数依次设置为n=256，m=20，k=15．与其他编码方法相比，KDN-FV编码方法取得了更高的分类结果，比原始Fisher向量编码方法高出1.9%．

此外，KDN-FV编码方法在Caltech 256和15-Scene数据集上也取得了较好的分类结果．它优于原始Fisher向量编码方法，并在两个数据集上分别高出3.1%和1.6%．同时，与SDFV和LGM方法相比，KDN-FV在15-Scene数据集上的分类结果也有一定的提升．

3.4 基于CNN局部特征的KDN-FV图像表达

将AlexNet[5]预训练模型最后一个全连接层的输出作为特征，并与3种不同的表达策略进行比较：(1)全局CNN特征，即直接使用全连接层的输出作为图像表达．(2)CNN多尺度无序汇集[34]，即multi-scale orderless pooling CNN(MOP-CNN)．这种方法以多尺度采样的方式在图像中提取CNN局部特征，并将这些特征进行VLAD或Fisher向量编码，形成图像表达．(3)CNN 多尺度金字塔汇集[35]，即multi-scale pyramid pooling CNN(MPP-CNN)．该方法以多尺度采样的方式在图像中提取CNN局部特征，并引入金字塔策略，最终将这些特征进行Fisher向量编码，形成图像表达．在实验过程中，使用与待比较方法相同的采样策略和设置进行CNN局部特征采样，并用KDN-FV编码代替对应的编码方法来构建图像表达．其中对于MOP-CNN(KDN-FV)以及MPP-CNN(KDN-FV)方法，所采用的参数设置为n=512，m=40，k=25．表2列出了相应的比较结果．

表2 基于CNN特征的KDN-FV图像表达分类性能

从表2可以看出，当用KDN-FV编码方法替代被比较方法中的编码方法后，新构建的图像表达具有更强的区分能力，这也说明了KDN-FV编码方法同样适用于CNN局部特征．

3.5 结果分析

从上述实验结果可以看出，KDN-FV编码方法既适用于DenseSIFT手工特征，也适用于由CNN网络提取出来的深度特征．文献[15，17-18]指出局部性约束的引入可以提升Fisher向量的区分能力．而KDN-FV在引入局部性约束的同时，又利用子模型拓扑结构的差异对视觉单词进行了筛选．它在Pascal VOC 2007和Caltech 256数据集上分别取得了64.6%和55.2%的分类精度，进一步提升了Fisher向量的表达能力．由此可以看出所提方案的有效性．

3.6 时耗性能分析

与原始Fisher向量编码方法相比，改进的KDN-FV编码方法增加了单词筛选步骤．为了分析KDN-FV编码方法的时间复杂性，采用与文献[14，21]相同的策略，比较了KDN-FV编码方法与原始Fisher向量编码方法的单幅图像平均编码时耗．在实验过程中，从Pascal VOC 2007数据集中选取了1 000幅图像，并将所有图像缩放为200×200，字典中单词个数为128．硬件配置为Intel i5 6 600 KB 3.5 GHz CPU，16 GB内存．经测试，Fisher向量编码方法单幅图像编码时间约为1 530 ms，而KDN-FV则为1 317 ms．实验表明，KDN-FV编码方法的时耗较少，这是因为即使KDN-FV中增加了单词筛选环节，但在编码阶段，KDN-FV将每一个局部特征仅仅投影到所筛选出的视觉单词即可，而原始Fisher向量编码方法需要计算所有视觉单词上的投影．由于单个单词的投影过程计算量较大，而KDN-FV编码方法仅需计算部分投影，这就减少了该方法的编码时间．

4 结 语

针对原始Fisher向量编码方法在编码过程中存在的全局编码以及未考虑视觉单词之间拓扑结构差异的问题，本文提出了一种基于k密集近邻算法的局部Fisher向量编码方法．该方法依据图像特征空间的流形结构，利用k密集近邻算法为每一个特征描述符筛选编码时所需的高斯子空间．KDN-FV编码方法在编码过程中引入了局部性约束，并且考虑了子空间之间的异同性，克服了原始Fisher向量编码方法存在的问题．通过在多个数据集上进行测试，结果显示改进后的方法增强了图像表达向量的区分能力，提升了分类精度，提高了编码效率．