快速路上匝道瓶颈路段异质交通流演变规律

吴德华 陈家伟 彭锐 赵明鹃

摘 要：为了掌握快速路瓶颈路段异质交通流的演变规律，以缓解交通拥堵，本文以快速路上匝道瓶颈路段为研究对象，构建了考虑安全距离的改进NaSch上匝道模型，利用数值仿真，对不同场景交通流演化过程进行系统性研究。仿真结果显示：在不同条件下，异质交通流中自动驾驶车辆比例的增加对瓶颈路段交通运营状态影响结果各异。在自由流阶段，自动驾驶车辆比例的增加对快速路瓶颈路段运营通行能力的增加无显著影响，自动驾驶车辆比例取0.9时，瓶颈路段运营通行能力反而降低了2.48%;在交通拥堵状态下，当异质交通流中自动驾驶车辆比例达到0.7及以上时，才有助于交通拥堵的消散，且其临界值随交通拥堵状态程度的提高而增大;当交通密度达到100 veh/km以上时，自动驾驶车辆比例的增加无法实质性改善瓶颈路段交通拥堵状态。研究结果可为异质交通流环境下的快速路上匝道瓶颈路段的治堵策略提供理论依据。

关键词：交通工程;交通拥堵;数值仿真;瓶颈路段;异质交通流

中图分类号：U491.2   文献标识码： A

道路瓶颈路段是导致交通拥堵的重要根源之一。研究道路瓶颈路段的交通流演化规律，有助于提高道路瓶颈路段的运营通行能力。特别是随着汽车产业与人工智能、物联网、云计算等新一代信息技术深度融合发展，自动驾驶车辆将逐步普及，未来传统车辆和自动驾驶车辆将在道路上长期同时存在，这种由传统车辆和自动驾驶车辆（协同自适应巡航车辆，cooperative adaptive cruise control，简称CACC车辆[1-3]）组成的交通流称之为异质交通流。在异质交通流环境下，道路瓶颈路段的交通流状态演化将更加复杂多变，其状态演化过程与传统驾驶行为、异质交通流的组成、限速控制等都有明显的关系[4-9]。新老问题叠加使城市道路瓶颈路段交通拥堵现象更加复杂。

美国加州伯克利PATH实验室为异质交通流研究提供了大量的实验数据。国内外许多学者在此基础上建立了相应的仿真平台，分析了异质交通流的稳定性并生成了异质流基本图模型，初步总结了异质交通流环境下的交通流演化过程[10-11]。为了再现不同交通场景下交通流演化过程，元胞自动机模型被广泛应用于交通流仿真数值模拟。此后大量学者鉴于184号规则在重现真实交通特性上的不足，提出改进的NaSch模型，取得相应的研究成果[12-13]。这些研究较少涉及异质交通流环境下道路瓶颈路段（上匝道）的交通流演变机制。由于道路瓶颈路段的交通流演变与道路平直路段存在较大差异，特别是在异质交通流环境下，道路瓶颈路段交通拥堵发生的物理机制十分复杂，因此认清其演变规律显得十分迫切。

本文以快速路上匝道瓶颈路段为研究对象，提出改进的NaSch上匝道模型，利用数值仿真，对不同场景交通流演化进行系统性分析，再现其交通流演变过程，从而揭示道路瓶颈路段交通流演变内在规律，为将来异质交通流环境下的快速路上匝道瓶颈路段的治堵策略提供理论依据。

1 考虑安全距离的改进NaSch上匝道模型

考虑异质交通流中，传统车辆和自动驾驶车辆由于车辆的速度、加速度及反应时间不一样，对驾驶行为存在不同的影响，Gipps考虑了车辆的加速度约束和安全距离约束，提出了安全距离模型[14-15]：

驾驶人期望与前导车保持安全车头间距，当前导车突然制动时，驾驶人能够有时间做出反应并减速停车，以避免发生碰撞。车辆安全距离模型见图1。

根据安全距离计算原理，有：

Dsafe，n=vn（t）τn+v2n（t）2bn-v2n+1（t）2bn+1。 （1）

式中：Dsafe，n表示车辆n所需要的安全距离;vn（t）表示车辆n在t时的速度，vn+1（t）表示车辆n+1在t时的速度;bn、bn+1分别表示车辆n和车辆n+1的最大减速度，通常情况bn+1=bn;τn表示车辆n的驾驶员反应时间。在异质交通流中，传统人工驾驶车辆和自动驾驶车辆最大的不同就是驾驶员反应时间的不同，参考以往研究成果，一般情况下，传统人工驾驶取1.5 s，自动驾驶车辆取05 s[3]。

根据Gipps模型进一步推导，得到车辆n相应的行驶安全速度：

vsafe，n（t）=-bnτn+

b2nτ2n+bn2Δxn（t）-Ln+1-τnvn（t）+v2n+1（t）bn。（2）

式中：Δxn（t）为车辆n与其前导车的车头间距，Δxn（t）=xn+1（t）-xn（t），xn+1（t）、xn（t）分别为车辆n+1和车辆n所处的位置;Ln+1为车辆n+1的车身长度，其余符号同式（1）。

改进的NaSch 模型，从t到t+1时，其交通演化规则如下：

（1）加速规则

当Dn>Dsafe，n时，即车辆n行驶过程中与其紧前车辆n+1之间的车间距大于该车行驶所需要的安全距离，车辆加速：

vn（t+1）→min（vn（t）+an，Vmax，vsafe，n（t），Dn）。

（3）

（2）匀速规则

当Dn=Dsafe，n时，即车辆n行驶过程中与其紧前车辆n+1之间的车间距等于该车行驶所需要的安全距离，车辆保持原速行驶：

vn（t+1）→min（vn（t），Dn）。 （4）

（3）減速规则

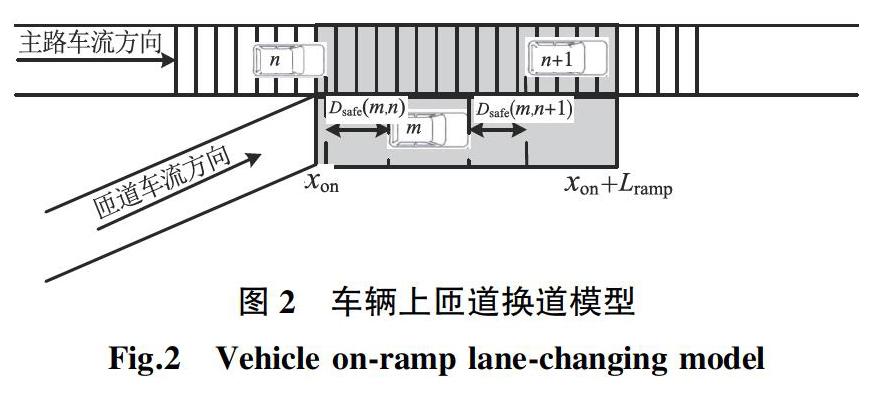
当Dn

vn（t+1）→max{min（vsafe，n（t），Dn-1），0}。（5）

（4）随机慢化概率

由于驾驶员在驾驶过程中存在驾驶行为不确定性，行驶过程中车辆按照随机慢化概率进行速度慢化，按照常规减速度进行减速：

vn（t+1）→max{min（vn（t）-bn，vn（t+1）），0}。 （6）

（5）位置更新

在速度演化更新规则的基础上，进行车辆位置更新：

xn（t+1）→xn（t）+vn（t+1）。 （7）

（6）上匝道换道规则

上匝道车辆换道规则采用加速道和虚拟匝道模型相结合的改进模型，即车辆从匝道进入加速道加速（或减速）行驶，同时判断进入主路前，主路是否满足车辆可插入的安全距离。当满足安全距离时，匝道上的车辆以加速道上行驶的速度换道进入主路。其判断过程如下：匝道上第m车辆进入里程范围[xon，xon+Lramp]，且存在车辆m与主路上第n辆及第n+1辆车的间距大于安全距离的间隙，即当D（m，n+1）>Dsafe（m，n+1），且D（m，n）>Dsafe（m，n）时，匝道上车辆以加速道上行驶的速度换道进入主路。车辆上匝道换道模型见图2。

2 数值仿真实验

利用MATLAB进行数值仿真：设置主路长度为8 500 m，匝道长度为5 500 m，主路设计车速为120 km/h，匝道设计车速为40 km/h，主路上游起点速度设置为115 km/h，限速段最大速度为80 km/h，合流段最大速度为50 km/h。上匝道示意图见图3。仿真模拟上匝道采用虚拟匝道和加速道结合的方式。模型中各项参数设定如下：车辆长度为6.5 m，每个元胞长度为0.5 m，常规减速度为2.5 m/s2，紧急减速度为3.5 m/s2，常规加速度为3 m/s2，自动驾驶反应时间为 0.5 s，传统驾驶反应时间为1.5 s。

为了观测异质交通流中自动驾驶车辆比例不同时快速路上匝道瓶颈路段交通量的变化情况，设置主路和匝道不同的进车概率，得到瓶颈路段的交通量演化过程，如图4所示。图中p表示自动驾驶车辆比例取值。

图4中，（1）～（6）图分别表示自动驾驶车辆比例p为0、0.1、0.3、0.5、0.7、0.9时，在主路和匝道不同进车概率场景下，合流段的平均交通量变化情况。从图中可以看出两个基本趋势：随着主路和匝道进车概率的增加，快速路合流段的交通量逐步增大;随着异质交通流中自动驾驶车辆比例的增大，快速路合流段的交通量逐步增加。

3 仿真结果分析

为了进一步深入分析自动驾驶车辆不同比例和主路及匝道不同进车概率场景下，快速路上匝道瓶颈路段的交通流状态演变过程，选择主路及匝道不同进车概率匹配场景，各仿真数据见表1～4。

当主路和匝道进车概率均为0.1时（见表1），主路交通量随自动驾驶车辆比例的增加，在335～384 vel/h之间变化，匝道交通量在276～295 vel/h之间变化，道路合流段的平均交通量在590～661 vel/h之间震荡，合流段的平均车速维持在46.2～47.4 km/h之间，道路合流段的交通量增加不明显，在p=0.9时交通量反而降低了2.48%。分析结果表明：在自由流阶段自动驾驶车辆比例的增加对快速路瓶颈路段运营通行能力的增加无显著影响。

当主路和匝道进车概率均为0.2时（见表2），合流段的平均交通量从862 vel/h逐步增加到1 150 vel/h，合流段的平均速度在p=0、0.1时出现交通拥堵状态，平均车速降低到10 km/h以内，分别为5.9、6.4 km/h。之后随着自动驾驶车辆比例的增加，交通拥堵逐渐消散，车速恢复到正常行驶状态。并且随着自动驾驶车辆比例的增加，合流段平均交通量逐步增加，当p=1.0时，合流段交通量相比p=0时的交通量，最大增幅达到33.41%。分析结果表明：在该场景下，自动驾驶车辆比例的增加可以显著提高快速路瓶颈路段的运营通行能力。

当主路进车概率为0.3、匝道进车概率为0.2时（见表3），合流段交通量出现交通拥堵状态。在p=0.7、0.9、1.0之后，合流段平均车速才逐步增加到20 km/h以上。随着自动驾驶车辆比例的增大时，合流段的交通拥堵逐步消散，当p=1.0时，合流段的平均交通量最大达到1 351 vel/h。分析结果表明：在该场景下，只有当异质交通流中自动驾驶车辆比例达到0.7及以上，才有助于交通拥堵的缓解和消散，且随着自动驾驶车辆比例的增加，快速路瓶颈路段的通行能力得到显著的提高。

当主路和匝道进车概率均为0.5时（见表4），合流段的平均交通量从849 vel/h逐步增加到1 307 vel/h，合流段的平均密度在100 veh/km以上，平均速度维持在5.0～6.4 km/h之间。虽然快速路瓶颈路段的通行能力仍然随着自动驾驶车辆比例的增加而增加，但是合流段的平均車速没有显著提高，说明交通拥堵状态无法得到实质性的改善。在主路和匝道进车概率取0.7和0.9时，得到类似的仿真数据，且快速路瓶颈路段的通行能力在自动驾驶车辆比例p=1.0时稳定在1 300～1 350 vel/h之间。

4 结论

通过仿真数据分析，在自由流阶段，异质交通流中自动驾驶车辆比例的增加对快速路瓶颈路段运营通行能力的增加无显著影响;在自由流与交通拥堵状态之间，自动驾驶车辆比例的增加可以显著提高快速路瓶颈路段的运营通行能力;在交通拥堵状态下，自动驾驶车辆比例达到较高时才能出现缓解和消散交通拥堵的显著效果，且其临界值随交通拥堵状态程度的提高而提高;在严重交通拥堵状态下，自动驾驶车辆比例的增加无法实质性改善交通拥堵。论文只针对主路和上匝道均为单车道构成的快速路瓶颈路段进行研究，后续研究将拓展到双车道和多车道构成的快速路瓶颈路段。

参考文献：

[1]WANG C J， GONG S Y， ZHOU A Y，  et al. Cooperative adaptive cruise control for connected autonomous vehicles by factoring communication-related constraints[J]. Transportation Research Procedia，  2019， 38： 242-262.

[2]ZHU Y H，  ZHAO D  B，  ZHONG Z G.  Adaptive optimal control of heterogeneous CACC system with uncertain dynamics[J]. IEEE Transactions on Control Systems Technology，  2019，  27 （4）： 1772-1779.

[3]华雪东，  王炜，  王昊. 考虑车与车互联通讯技术的交通流跟驰模型[J]. 物理學报， 2016，  65（1）： 010502.

[4]Gong S Y， Du L L. Cooperative platoon control for a mixed traffic flow including human drive vehicles and connected and autonomous vehicles[J]. Transportation Research Part B，  2018，  116：  25-61.

[5]LIU H，  KAN X G，  SHLADOVER S E， et al. Impact of cooperative adaptive cruise control on multilane freeway merge capacity[J]. Journal of Intelligent Transportation Systems，  2018，  22（3）： 263-275.

[6]GHIASI A， HUSSAIN O， QIAN Z， et al.  A mixed traffic capacity analysis and lane management model for connected automated vehicles：  A Markov chain method[J].  Transportation Research Part B，  2017，  106：  266-292.

[7]GONG S Y， SHEN J L， DU  L L.  Constrained optimization and distributed computation based car following control of a connected and autonomous vehicle platoon[J].  Transportation Research Part B， 2016，  94：  314-334.

[8]ZHOU Y，  AHN S Y， CHITTURI M， et al.  Rolling horizon stochastic optimal control strategy for ACCand CACC under uncertainty[J]. Transportation Research Part C，  2017，  83：  61-76.

[9]QIN W B B， OROSZ G.  Scalable stability analysis on large connected vehicle systems subject to stochastic communication delays[J]. Transportation Research Part C，  2017，  83：  39-60.

[10]秦严严，  王昊，  王炜，  等. 混有协同自适应巡航控制车辆的异质交通流稳定性解析与基本图模型[J]. 物理学报，  2017，  66（9）： 094502.

[11]姚志洪， 蒋阳升， 王逸， 等. 车联网环境下的动态异质交通流车队离散模型[J]. 北京交通大学学报， 2019，  43（2）： 107-116.

[12]李新刚. 基于元胞自动机模型的交通系统微观建模与特性研究[D]. 北京：  北京交通大学， 2009.

[13]马丽娜. 基于元胞自动机的自动驾驶-手动驾驶交通流特性研究[D]. 成都：  西南交通大学， 2017.

[14]GIPPS P G.  A behavioral car-following model for computer simulation[J].  Transportation Research Part B，  1981，  15（2）： 105-111.

[15]王殿海，  金 盛. 车辆跟驰行为建模的回顾与展望[J]. 中国公路学报，  2012，  25（1）：  115-127.

（责任编辑：曾 晶）

Heterogeneous Traffic Flow Evolution Rule in Expressway

On-ramp Bottleneck Section

WU Dehua*， CHEN Jiawei， PENG Rui， ZHAO Mingjuan

（College of Civil Engineering， Fuzhou University， Fuzhou 350116， China）

Abstract：

To grasp the evolution rule of heterogeneous traffic flow on expressway bottleneck section and alleviate traffic congestion， the paper takes expressway on-ramp bottleneck section as study object. An improved NaSch on-ramp model considering safety distance was constructed， and the evolution of traffic flow in different scenarios was systematically studied by numerical simulation. The simulation results show that the increase of the proportion of autonomous vehicles in heterogeneous traffic flow has different effects on the transit operation of the bottleneck section. When the proportion of self driving vehicles is 0.9， the traffic capacity of the merging section was reduced by 2.48% in the free flow phase.When the proportion of self driving vehicles in heterogeneous traffic flow reaches 0.7 or more in the stage of traffic jam， it will help to dissipate the traffic congestion， and its critical value will increase with the increase of the degree of traffic congestion.When the traffic density reaches more than 100 veh/km， the increase of the proportion of self driving vehicles can not substantially improve the traffic congestion in bottleneck sections. The research results can provide theoretical support for the congestion control strategy on the expressway on-ramp bottleneck section.

Key words：

traffic engineering;traffic congestion; numerical simulation;bottleneck section; heterogeneous traffic flow

收稿日期：2020-02-17

基金項目：福建省自然科学基金资助项目（2016J01230）;福州大学本科生科研训练计划资助项目（2019-25105）

作者简介：吴德华（1978-），男，副教授，博士，研究方向：交通安全与交通规划，Email：610706517@qq.com.

通讯作者：吴德华，Email：610706517@qq.com.