应力波在散体颗粒中的传播规律

王秉相，程普锋，郑宇轩，周风华

（宁波大学冲击与安全工程教育部重点实验室，浙江 宁波 315211）

砂石等脆性材料由大量的脆性散体颗粒组成，具有松散、多孔、易压缩等特性[1-2]，应力波在此类松散脆性材料中的传播[3]通常会呈现显著的衰减规律。散体脆性颗粒作为消波耗能材料已被广泛应用于防护领域，用作冲击、爆炸等的能量吸收[4-5]。因此，深入探讨应力波在散体脆性颗粒中的传播规律和影响因素对防护工程具有重大意义，亦可为防护层的构建提供一定的理论参考。

季顺迎等[6]用石质球体作为冲击物，在散体颗粒底部安装压力传感器，通过散体颗粒底部压力的变化来分析其缓冲性能，研究了颗粒粒径、颗粒形态等对缓冲性能的影响，由于石质球与颗粒接触过程存在不均匀性，因此实验结果的精度不高。赵跃堂等[7]基于平面波加载器，通过在不同深度土层中埋设压力传感器的方法来探究饱和土颗粒在爆炸加载下不同层的压力变化，根据不同土层的压力分布来分析波的传播规律，由于在土颗粒中埋设压力传感器会改变土颗粒的内部结构，因此该方法测得的压力值与真实值存在一定差异。赵凯[8]实验研究了爆炸载荷作用下多层防护层结构对爆炸波的衰减作用，获得了多种分配层下波的衰减规律。魏久淇等[9]基于分离式霍普金森压杆实验，通过透射杆峰值应力与入射杆峰值应力的比值来描述波的衰减，并探究了中高应变率下钙质砂的力学响应。由于钙质砂与透射杆之间存在较大的机械阻抗，直接将透射杆峰值应力作为砂粒端面应力的处理方式对波衰减的准确性有一定影响。Yu 等[10]通过改进SHPB 装置，将入射波、反射波、透射波相结合来计算试件两端的峰值应力，提出了一种定量计算珊瑚砂试件中应力波衰减规律的新方法，能更准确地得到试件两端面的应力峰值，由于该数据分析方法是基于一维单向应力波传播理论，而应力波在散体颗粒中传播时可能会发生透射和反射，将涉及更复杂的多向波系，因此该方法存在一定误差。

目前，应力波在散体颗粒中传播规律的实验研究尚不成熟，而数值模拟可以避免实验存在的一些技术难题，定性或半定量地分析散体颗粒中波的传播规律。祁原等[11]利用离散元软件PFC2D分析了可破碎颗粒在循环载荷下的耗能特性，并探究了颗粒破碎与系统能量耗散率的关系。郑文[12]、黄俊宇[13]通过PFC3D建立散体颗粒模型，研究了石英砂颗粒在动载荷下的力学响应。迄今为止，数值模拟研究更多关注散体颗粒本构模型的构建和动态力学性能，散体颗粒中应力波的传播规律尚缺乏系统研究。

本研究基于离散元颗粒流软件PFC3D建立典型的石英砂颗粒模型，在保证模型颗粒与实际颗粒等粒径的前提下，通过模型的等比例缩放，模拟侧限条件下石英砂的动态压缩实验，并与实验侧限压缩本构[14-16]进行对比，验证本模型参数的合理性，在此基础上研究冲击载荷下应力波在散体颗粒中的传播规律和影响因素。

1 离散元模型

PFC3D模型是由若干基础颗粒（刚性颗粒）通过一定的黏结键组成的，通过定义基础颗粒间的微观参数来建立与模拟材料具有相同宏观力学性能的离散元模型。由于离散元模型中的微观参数难以通过实验手段直接获得，且尚无有效的理论将其与实际材料的宏观力学特性进行关联，因此目前均通过数值模拟校准的方法建立二者之间的联系[17]。对于散体颗粒，土力学中常采用侧限压缩本构模型[18-20]来表示其本构关系，即通过孔隙比-轴向应力曲线来描述颗粒材料的压缩、变形及破碎过程[21]。

建立如图1 所示的簇颗粒模型来表述单个脆性颗粒，每个簇由60～70 个基础颗粒组成，由于实际砂颗粒内部存在缺陷和孔隙，删除10%～20%的基础颗粒来模拟实际颗粒的不规则外形和风化腐蚀等对砂砾造成的损伤，通过调整簇中基础颗粒的大小和颗粒间的孔隙以满足实际颗粒尺寸，并保证簇的密度同实际砂粒密度一致。选取石英砂为典型的砂砾代表，其密度为2 636 kg/m3。通过Flat-Joint 黏结模型将松散的基础颗粒用黏结键黏结，当基础颗粒间的法向接触力或切向接触力超过其临界值时，黏结键将发生破坏失效。表1 为石英砂采用Flat-Joint 黏结模型时所对应的微观参数，其中Emod为接触模量，Fj-Kn为法向刚度，Fj-Ks为切向刚度，Fj-Coh为切向黏结强度，Fj-Ten为法向黏结强度，Damp为阻尼系数。

图 1 簇颗粒的生成过程Fig. 1 Generation process of cluster particle

表 1 Flat-Joint 模型微观参数Table 1 Micro-parameters of the Flat-Joint model

单个石英砂颗粒的粒径分布控制在150～250 μm之间，以42% 的自然堆积孔隙率生成散体颗粒，石英砂颗粒内部采用Flat-Joint 黏结键黏结，颗粒之间为线性接触。在保证粒径大小同实际一致的情况下对模型进行等比例缩放，生成直径为2.2 mm、高为0.6 mm 的圆柱体试样，如图2 所示。圆柱体试样的上、下压板层设置为刚性墙体，径向为刚性约束，保持下底板不动，对上压板向下持续施加10 m/s 的加载速度，得到图2 中的归一化孔隙比-轴向应力曲线，模拟结果与文献[13]中的实验结果整体吻合较好，屈服应力均为10 MPa 左右。

图 2 石英砂压缩曲线Fig. 2 Compression curve of quartz sand

2 散体颗粒中应力波的传播规律

如图3 所示，建立直径为1 mm、高为3.6 mm的圆柱试件，径向为刚性约束，下端面为自由面，上端面向下施加一个速度为50 m/s 的冲击加载，由于颗粒间应力分布的离散性较大，在试件内部引入测量球，通过测量球所在空间位置全部粒子的应力平均值来描述应力波幅值，测量球球心所在位置为应力波传播的距离，通过不同位置测量球测得的应力幅值来表征应力波在散体颗粒中的传播规律。图4 给出了试件不同位置的应力波波形。整体而言，随着传播距离的增大，应力波峰值逐渐减小，应力波脉宽逐渐发散。

图 3 散体颗粒模型及测量球位置Fig. 3 Particle model and positions of the measurement balls

采用观察区域内的应力平均值来表征应力波的传播规律，测量球对应力波传播可能存在一定影响。由于研究内容为轴向的应力波在散体颗粒中的传播规律，因此将测量球的球心固定在圆柱试件的中心轴上，通过改变测量球的直径大小d 来研究测量球对应力波传播规律的影响。图5给出了通过不同直径大小的测量球获得的应力波衰减规律。整体来看，所有衰减规律的变化趋势是一致的，但测量球直径越大，应力波衰减越严重。测量球获得的平均应力并非一维应力波，同时涉及了圆柱径向的应力波衰减，故测量球直径越大，横向衰减考虑的也越多。归一化峰值应力，无量纲化应力波传播距离， 其中， σs为 当前峰值应力， σ0为初始峰值应力，Ls为应力波传播的距离，D 为圆柱试件的直径。

图 4 试件不同位置的应力波波形Fig. 4 Stress wave forms at different positions of the test piece

图 5 不同直径的测量球对应力波衰减的影响Fig. 5 Effect of measuring ball diameter on the attenuationof stress waves

如果测量球直径过小，由于散体颗粒较大的分散性导致测量区域的应力波动较大；而当选取的测量球直径过大，特别是接近试件直径时，将导致测量的区域靠近侧面固壁端的应力加倍。本研究选取测量球直径为试件直径的0.6 倍，此时应力波衰减趋于稳定。从图5 中可以看到，峰值应力随传播距离呈指数型衰减，具体可表示为

式中：A = 0.20，B = 0.76，β = 2.82。β 作为衰减因子，可以定量地描述应力波在散体颗粒中的衰减程度，β 越大，说明应力波衰减程度越大。

为更精确地研究应力波的衰减规律，在散体颗粒圆柱中引入更多测量球来观测试件不同位置的应力波形，取各处应力波峰值，归一化后绘于图6(a)。整体而言，归一化峰值应力仍然呈现近似指数型衰减规律，通过对局部数据点拟合可以得出，在传播前期应力波衰减明显，对应的衰减因子β = 5.40；而在传播的中后期，应力波衰减程度趋缓，对应的衰减因子β = 1.16，远小于前期的衰减因子。对照应力波传播过后的颗粒细观结构，如图6(b)所示，其中红色区域代表颗粒间黏结键的断裂。前期应力波衰减显著的区域正好对应于颗粒大量破碎的区域，将其定义为破碎区，中后期衰减因子较小的区域正好对应于颗粒较少甚至没有发生破碎的区域，将其定义为微/未破碎区。由图6 可知，颗粒的破碎区主要集中在试件的加载端，而恰好加载端附近区域的峰值应力衰减最为严重，远离加载端的微/未破碎区的颗粒破碎程度显著低于破碎区，对应的应力波峰值应力衰减不明显，趋于稳定，说明颗粒的破碎和应力波衰减具有直接关系。

图 6 应力波衰减规律及颗粒破碎Fig. 6 Attenuation law of the stress wave and the image of particle fragmentation

3 散体颗粒中应力波衰减的影响因素

3.1 颗粒破碎对应力波衰减的影响

将图3 离散元模型中颗粒内部的黏结键强度设置为1 000 MPa（正常情况为50 MPa），在数值模拟过程中黏结键将不发生断裂，即颗粒不破碎，保持其他微观参数不变，在50 m/s 的加载速度下进行数值模拟对比。将应力波在不同位置的峰值应力绘于图7，并用式（1）进行拟合，可得不破碎颗粒中的应力波衰减因子β = 1.20，而正常黏结强度下的可破碎颗粒在微/未破碎区中应力波衰减因子β = 1.16，两者相差无几。

将正常黏结强度下的可破碎颗粒在破碎区中的应力波峰值应力进行拟合，得到应力波衰减因子β = 5.40，显著大于不可破碎颗粒的应力波衰减因子（β = 2.92），如图8 所示。颗粒破碎过程中，基础颗粒间的黏结键断裂需要消耗能量，并且颗粒破碎使整个散体颗粒系统中的力链更加复杂，由于应力波是单向传播，且颗粒间具有复杂的应力波透反射现象，因此宏观上表现为应力波峰值应力大幅衰减，卸载波形严重弥散。

图 7 不同区域拟合曲线无量纲传播距离Fig. 7 Dimensionless propagation distance of fitted curves in different regions

为深入研究应力波衰减过程中局部衰减因子β 与颗粒局部破碎程度的关系，设定基础颗粒间的黏结键强度范围为20～100 MPa，数值模拟得到颗粒在破碎区的局部破碎程度为8%～60%，对应破碎区局部的应力波衰减曲线指数拟合得到β 为3.50～6.10。如图9 所示，β 和颗粒的破碎程度具有显著的正相关性，即β 随颗粒破碎程度的增加而增大，近似呈指数关系，说明颗粒破碎是影响散体颗粒中应力波衰减的一个重要因素。

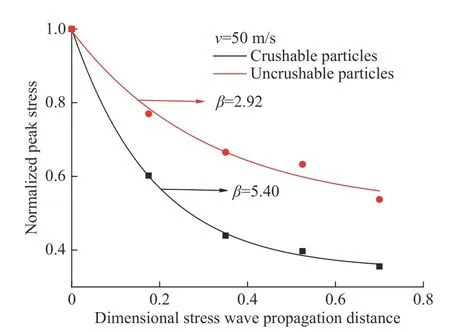
图 8 应力波在颗粒破碎/不破碎时的衰减规律Fig. 8 Attenuation laws of stress wave when particles are broken/unbroken

图 9 颗粒破碎程度随衰减因子β 的变化曲线Fig. 9 Degree of particle fragmentation with respect to the attenuation factor β

3.2 加载脉宽对应力波衰减的影响

应力波在散体颗粒间传播时会发生透射和反射，涉及复杂的多向波系，在弹性散体颗粒中会发生散射现象，即随着传播距离的增大，应力波脉宽会弥散，如图4 所示。应力波的衰减程度随着传播距离的增大而逐渐趋缓，除了受到颗粒破碎程度的影响之外，应力波的弥散也会对其产生一定的影响。为避免颗粒破碎带来的干扰，对不可破碎散体颗粒模型（黏结键强度为1 000 MPa）进行不同脉宽的冲击加载。图10 给出了相同峰值应力、不同脉宽的应力波随传播距离的衰减规律。由图10 可知，加载波形脉宽越大，应力波随传播距离增大所产生的峰值应力衰减越少，弥散也越小，加载初始，应力波具有相近峰值应力而脉宽不同，当传播一定距离之后，应力波具有相近脉宽而峰值应力不同。对不同脉宽的应力波传播过程中的峰值应力利用式（1）进行拟合，得到如图11 所示的拟合曲线和对应的衰减因子β。由图11 可知，随着应力波脉宽的增大，β 从1.46 减小到0.61，应力波脉宽亦能对应力波在散体颗粒中的传播产生较大影响。造成该现象的主要原因是：散体颗粒对高频波具有显著的弥散作用，会大幅削弱短脉宽的高频波峰值应力，而对于长脉宽的低频波影响相对较小。

图 10 不同脉宽的应力波传播规律Fig. 10 Propagation of stress waves with different pulse widths

图 11 不同脉宽的应力波峰值拟合曲线Fig. 11 Curves of stress wave peaks with different pulse widths

3.3 加载速度对应力波衰减的影响

图12 给出了散体颗粒在不同加载速度（30～110 m/s）下，应力波峰值随传播距离的衰减规律。从图12 中可以看出，加载速度越大，β 值越大，即应力波的衰减程度随着加载速度的增大而增大，在靠近加载端尤为明显。考虑到颗粒破碎是应力波衰减的重要影响因素，将颗粒内部的黏结键强度设置为1 000 MPa，此时，颗粒不发生破碎，拟合曲线如图13 所示。图13 结果表明，在颗粒不发生破碎的前提下，在一个较宽泛的加载速度（1～100 m/s）范围内，应力波在散体颗粒中的衰减规律基本不变。

图 12 不同加载速度下可破碎颗粒的峰值应力拟合曲线Fig. 12 Peak stress fitting curves of the crushable particles at different loading velocities

图 13 不同加载速度下不可破碎颗粒的峰值应力拟合曲线Fig. 13 Peak stress fitting curves of the uncrushable particles at different loading velocities

将加载速度、衰减因子β、颗粒黏结键的破碎比建立联系，如图14 所示。由图14 可知，随着加载速度的增大，β 呈上升趋势，应力波的衰减程度变大，观察黏结键的破碎比发现，随着加载速度的增大，其破碎比也呈增大趋势，且β 与黏结键的破碎比有相似的变化趋势。观察图14 中不破碎颗粒的衰减因子，可以看到不同加载速度对不破碎颗粒的应力波衰减影响较小。由此可知，应力波衰减的速度相关性本质上是由散体颗粒的冲击破碎引起的，加载速度越大，颗粒破坏程度越大，进而应力波的衰减程度越大；而在颗粒不破碎的情况下，加载速度增大时，衰减程度变化不明显。

图 14 衰减因子、黏结键破碎比与加载速度的关系Fig. 14 Relationship between attenuation factor, bond breaking ratio and loading velocity

4 结 论

利用离散元颗粒流软件PFC3D建立了散体颗粒模型，通过侧限压缩实验验证了模型的准确性。基于该离散元模型，研究了散体颗粒在冲击载荷下应力波的传播规律和主要影响因素。主要结论如下。

（1）应力波在散体颗粒中传播时，其峰值应力呈指数型衰减，且脉宽逐渐弥散。衰减因子β 可定量描述应力波的衰减程度，β 值越大，应力波的衰减越显著。

（2）散体颗粒在冲击加载后，根据颗粒的微观破坏形貌，可分为破碎区和微/未破碎区，两者的峰值应力也均呈指数衰减。破碎区的衰减程度远大于微/未破碎区，颗粒的破碎是影响散体颗粒中应力波衰减的一个重要因素。

（3）加载脉宽是影响应力波在散体颗粒中衰减的另一个主要因素，加载脉宽越小，应力波峰值衰减越大。应力波在散体颗粒中的传播初期，应力峰值显著衰减，是颗粒破碎和短脉宽高频波的共同作用。

（4）应力波衰减与加载速度显著相关，应力波峰值应力衰减随加载速度的增大而增大。但实际上却是颗粒破碎在宏观上的表象，加载速度越大，颗粒破坏程度越大，进而应力波的衰减程度越大。如果颗粒不发生破碎，加载速度增大时，应力波在散体颗粒中的衰减变化不明显。