橡胶超弹性测试及其对轮胎有限元计算结果的影响
付新华,李 宁,郭渊昊,李 鹏
(三角轮胎股份有限公司,山东 威海 264200)
轮胎在接地时变形较复杂,受压缩、剪切及拉伸等多种变形共同影响,目前有限元分析一般采用基于单轴拉伸数据拟合的Yeoh或Neo-Hookean等超弹性模型进行表征[1-2]。本工作以实际测试数据及超弹性拟合数据分析研究这种表征方式的适用性及其与综合拉伸+剪切+压缩试验数据拟合得到的超弹性本构模型的精度差异。
1 试验测试
橡胶材料几乎不可压缩,因此一般用单轴拉伸、等双轴拉伸和平面拉伸等变形模式来表征橡胶材料的单轴拉伸/压缩、等双轴拉伸/压缩及平面拉伸/压缩等力学特性。
对某规格全钢子午线轮胎胶料进行单轴拉伸、等双轴拉伸和平面拉伸3种变形模式的测试,试验夹具如图1所示。将试验数据进行处理,得到3种变形模式的应力-应变曲线,并与拟合结果进行对比。

图1 试验夹具
2 不同变形模式试验结果拟合
目前有多种本构模型可以表征橡胶材料的超弹特性,除了上述两种模型外,还有基于热力学统计的Van der Waals模型和Arruda-Boyce模型及基于现象学的完全多项式模型和Ogden模型等。总体而言,基于变形张量I1的模型包括Neo-Hoohean和Yeoh等缩减多项式模型、Marlow模型和Van der Waals模型(β=0,β为变形张量I1和I2合成I的线性参数);基于I1和I2的模型包括Ogden模型和Van der Waals模型(β≠0)。这些模型的适用范围和拟合精度不同。下面以同种胶料试验为例研究不同变形模式组合时几种常用本构模型的拟合精度[3-4]。
2.1 单轴拉伸数据拟合
单轴拉伸数据拟合的Yeoh,Ogden和Van der Waals模型的应力-应变曲线与试验结果的对比分别如图2—4所示。由图2—4可以得出以下结果。
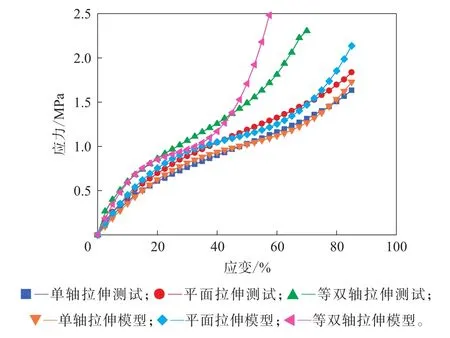
图2 单轴拉伸数据拟合的Yeoh模型的应力-应变曲线与试验结果的对比
单轴拉伸数据拟合得到的Yeoh模型表征的单轴拉伸曲线与测试数据匹配较好,平面拉伸变形拟合精度也较高,而等双轴变形模式下应变小于50%时也相对合理。
Ogden模型拟合出的单轴拉伸曲线与测试数据拟合较好,但另外两种变形模式与测试数据差别巨大,因此仅有单轴拉伸数据时不适宜用Ogden本构模型。
Van der Waals模型拟合出的单轴拉伸曲线与测试数据拟合较好,而另外两种变形模式与测试数据差别很大。
由此可见,在仅有单轴拉伸测试数据时,Ogden和Van der Waals模型的拟合精度不如Yeoh模型。
2.2 单轴拉伸+等双轴拉伸数据拟合
单轴拉伸+等双轴拉伸数据拟合的Yeoh,Ogden和Van der Waals模型的应力-应变曲线与试验结果的对比如图5—7所示。由图5—7可得出以下结果。

图3 单轴拉伸数据拟合的Ogden模型的应力-应变曲线与试验结果的对比
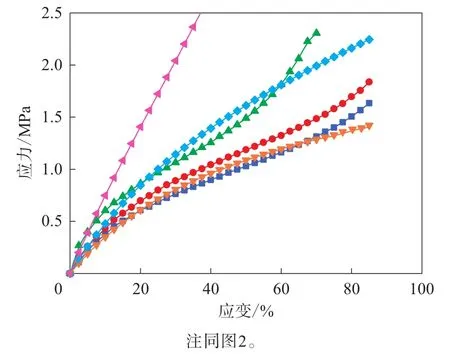
图4 单轴拉伸数据拟合的Van der Waals模型的应力-应变曲线与试验结果的对比

图5 单轴拉伸+等双轴拉伸数据拟合的Yeoh模型的应力-应变曲线与试验结果的对比
通过单轴拉伸+等双轴拉伸数据拟合Yeoh模型表征的等双轴变形模式曲线的精度比仅有单轴拉伸数据时得到很大提升。

图6 单轴拉伸+等双轴拉伸数据拟合的Ogden模型的应力-应变曲线与试验结果的对比

图7 单轴拉伸+等双轴拉伸数据拟合的Van der Waals模型的应力-应变曲线与试验结果的对比
通过单轴拉伸+等双轴拉伸数据拟合Ogden模型表征的单轴拉伸和等双轴拉伸变形模式曲线与测试数据拟合较好,但平面拉伸变形模式曲线与测试结果仍有差别。
通过单轴拉伸+等双轴拉伸数据拟合Van der Waals模型表征的3种变形模式曲线与测试数据拟合精度较高。
2.3 单轴拉伸+平面拉伸数据拟合
单轴拉伸+平面拉伸数据拟合的Yeoh,Ogden和Van der Waals模型的应力-应变曲线与试验结果的对比如图8—10所示。由图8—10可见以下结果。

图8 单轴拉伸+平面拉伸数据拟合的Yeoh模型的应力-应变曲线与试验结果的对比
通过单轴拉伸+平面拉伸数据拟合Yeoh模型表征的单轴拉伸和平面拉伸变形模式曲线与测试结果拟合非常好,等双轴变形模式曲线拟合精度也比仅有单轴拉伸测试数据时得到提升。

图9 单轴拉伸+平面拉伸数据拟合的Ogden模型的应力-应变曲线与试验结果的对比
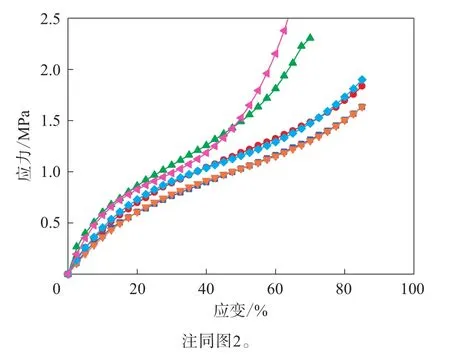
图10 单轴拉伸+平面拉伸数据拟合的Van der Waals模型的应力-应变曲线与试验结果的对比
通过单轴拉伸+平面拉伸数据拟合Ogden模型表征的单轴拉伸和平面拉伸变形模式曲线与测试结果拟合非常好,但等双轴变形模式曲线与测试结果差别巨大。
通过单轴拉伸+平面拉伸数据拟合Van der Waals模型表征的单轴拉伸和平面拉伸变形模式曲线与测试结果拟合度非常高,但等双轴变形模式曲线与测试数据仍有差距。
2.4 单轴拉伸+等双轴拉伸+平面拉伸数据拟合
单轴拉伸+等双轴拉伸+平面拉伸数据拟合的Yeoh,Ogden和Van der Waals模型的应力-应变曲线与试验结果的对比如图11—13所示。
由图11—13可见,通过3种变形模式数据拟合的Yeoh,Ogden和Van der Waals模型表征的单轴拉伸、平面拉伸和等双轴拉伸变形模式曲线与测试结果的拟合度均非常高。
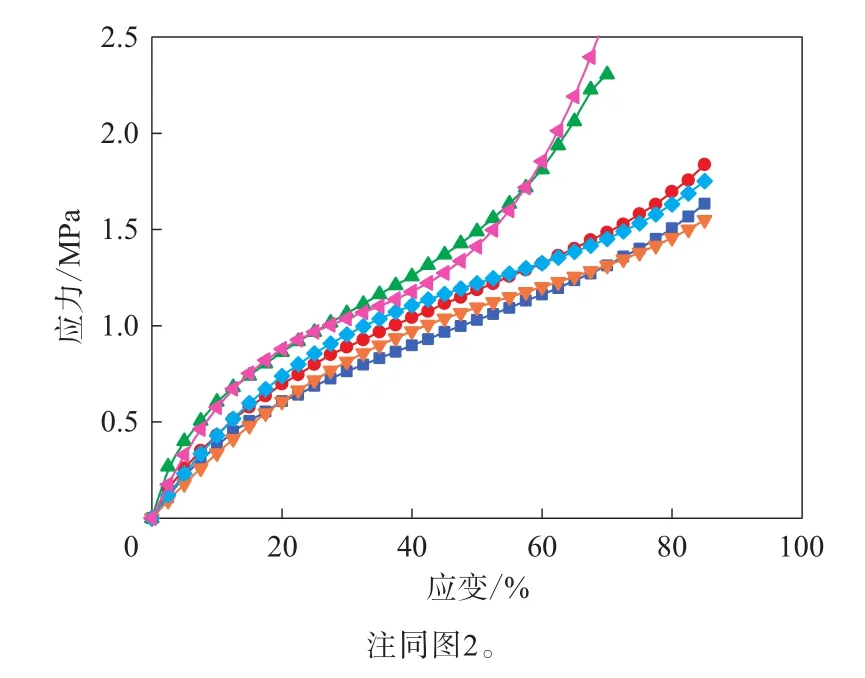
图11 3种变形模式测试数据拟合的Yeoh模型的应力-应变曲线与试验结果的对比
通过对Yeoh,Ogden和Van derWaals超弹性本构模型在不同变形模式试验数据下的拟合结果对比可以得到以下结论。

图12 3种变形模式测试数据拟合的Ogden模型的应力-应变曲线与试验结果的对比
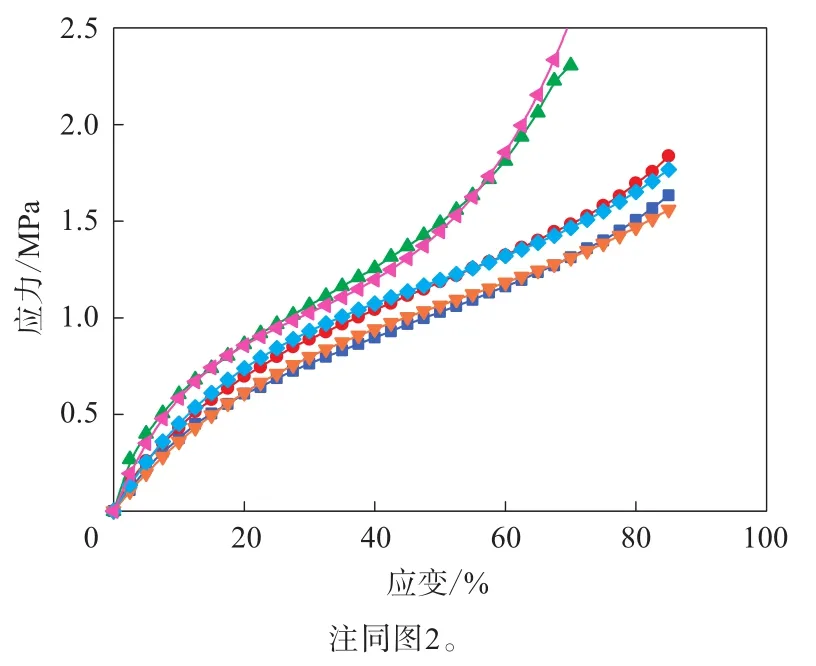
图13 3种变形模式测试数据拟合的Van der Waals模型的应力-应变曲线与试验结果的对比
(1)Yeoh模型随变形模式匹配拟合精度波动较小,因此仅有单轴拉伸数据时适宜用Yeoh模型。
(2)Ogden模型对任意一种或者几种变形模式的拟合精度都很高,也可以说该模型拟合时只对输入的变形模式的试验数据的精度负责,而其他变形模式则可能非常差,因此该模型适用于拟合变形模式全面的试验数据。
(3)等双轴拉伸试验数据是Ogden和Van der Waals模型拟合精度的关键,因为该变形模式表征胶料压缩特性,结合轮胎实际运动变形情况,仿真时所用本构模型最好能够表征等双轴拉伸变形。
(4)上述各本构模型对不同胶料的拟合精度也不尽相同,一方面与材料本身性能有关,同时对测试精度也有很高的要求。
3 仿真验证
以相同规格全钢子午线轮胎为例验证不同变形模式下的计算精度以及3种变形模式下Yeoh,Ogden和Van der Waals等模型的计算精度。具体验证思路如下。
(1)选单轴拉伸及单轴拉伸+等双轴拉伸+平面拉伸变形模式下结果进行变形模式对比。
(2)在单轴拉伸+等双轴拉伸+平面拉伸变形模式下对Neo-Hookean,Yeoh,Ogden和Van der Waals等本构模型进行对比。
3.1 局部受力对比
选择不同变形模式下的各本构模型进行标准负荷下的稳态滚动计算,并分别选择带束层端点和胎体反包端点区域的计算结果进行对比。
3.1.1 带束层端点
带束层端点区域受力分析见图14,提取其应变能密度和应变数据进行分析,结果如图15和16所示。

图14 带束层端点区域受力分析
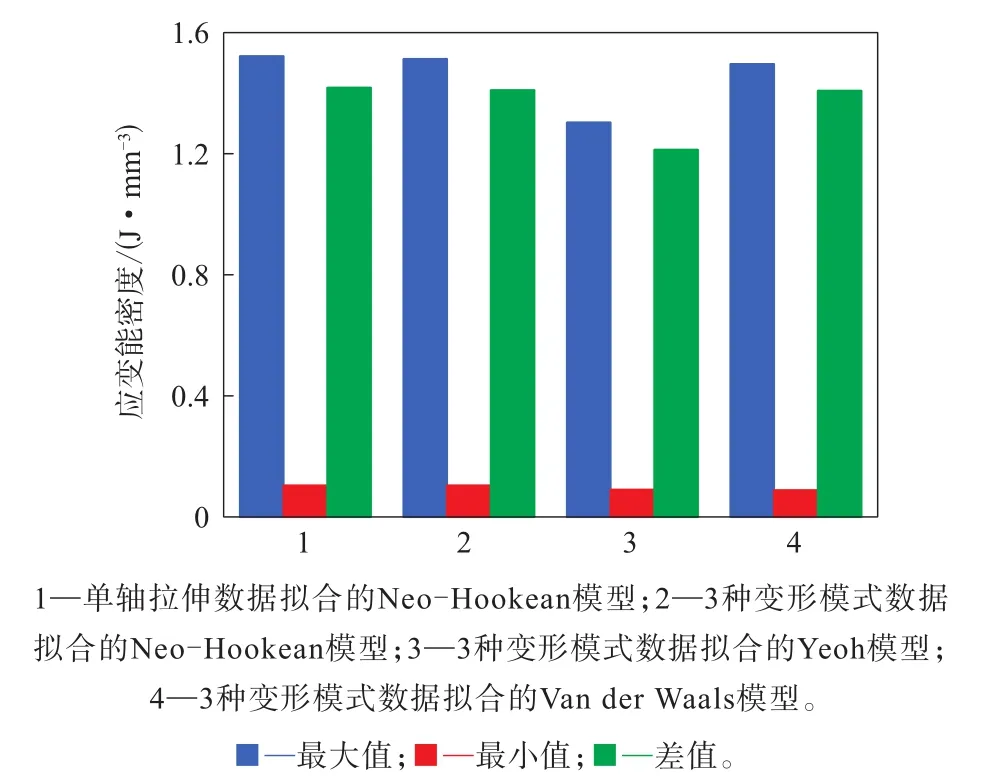
图15 带束层端点应变能密度幅值对比

图16 带束层端点剪应变幅值对比
由图15和16可见:应用不同变形模式拟合的同一本构模型带束层端点应变能密度和剪应变计算值的变化在3%~10%范围内;3种变形模式下不同本构模型计算值的变化在7%~15%范围内;Yeoh与Van der Waals模型计算值的最大差异约为8%。
3.1.2 胎体反包端点
胎体反包端点区域受力分析见图17,提取其应变能密度和应变数据进行分析,结果如图18和19所示。
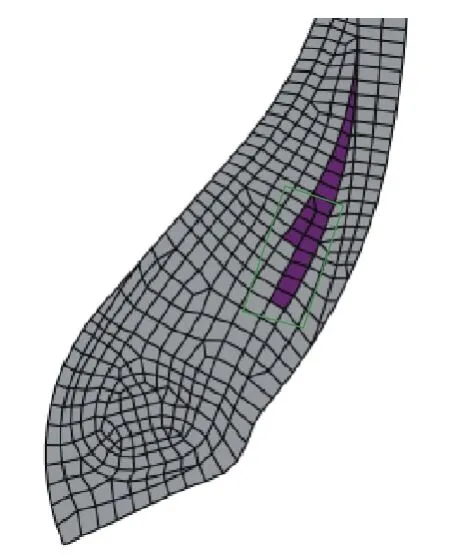
图17 胎体反包端点区域受力分析
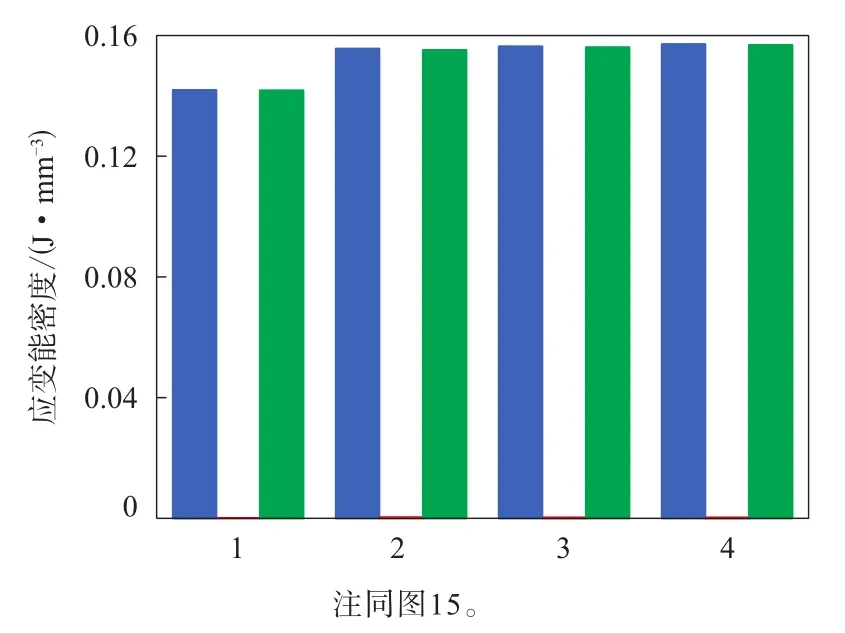
图18 胎体反包端点应变能密度幅值对比
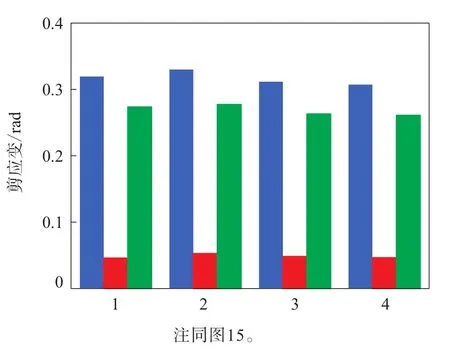
图19 胎体反包端点剪应变幅值对比
由图18和19可见:应用不同变形模式拟合的同一本构模型反包端点应变能密度和剪应变计算值的变化在9%~15%范围内;3种变形模式下不同本构模型计算值的变化在2%~13%范围内;Neo-Hookean与Van der Waals模型计算值的差异超过10%。
3.2 计算效率对比
对选用不同本构模型计算时的收敛情况及计算时间进行统计,结果如表1所示。

表1 不同本构模型计算时间统计
由表1可见:4种模型对两种胶料计算的迭代次数变化趋势不同,但各本构模型迭代次数差别不明显;不同模型对两种胶料的计算时间变化趋势也不相同,Yeoh和Van der Waals模型计算时间相对较短。
该结果仅是基于一款轮胎模型在只有超弹性表征下静载计算得到的,以说明不同本构模型在轮胎模拟计算中的区别。当轮胎模拟中同时涉及超弹性和粘弹性时需注意选择超弹性本构模型。
4 结论
通过对不同变形模式组合下Yeoh,Ogden和Van der Waals等本构模型拟合精度的分析,得到下述结论。
(1)当仅有单轴拉伸数据时适宜选择Yeoh模型,而用单轴拉伸+等双轴拉伸+平面拉伸3种变形模式数据能够更好地表征胶料在实际工况下的变形状态。
(2)在测试数据包括3种变形模式时,Van der Waals和Ogden模型的拟合精度相对较高,应用拟合精度较高的模型进行计算可以更好地表征轮胎各工况的实际受力状况,尤其是分析不同设计方案轮胎胎体反包端点和带束层端点等局部受力时能得到更准确的结果。
此外,当模型中涉及胶料的粘弹性时还要考虑超弹性与粘弹性的匹配问题。

