基于Spark的上下文感知推荐算法的研究
赵志伟
(星环众志科技(北京)有限公司,北京100044)
大数据时代的到来,给现代社会带来了巨大的影响。当用户在海量数据中查找信息时,需要投入很大的精力。为了解决用户筛选信息困难的问题,推荐系统逐渐进入我们的视野。推荐系统通过分析用户兴趣和项目属性之间的关系,能够帮助用户从大量的可选数据中快速定位到满足用户需求的信息[1]。
推荐系统的上下文感知算法是目前应用领域应用最多,也是最成功的一种推荐算法。
首先对原始矩阵进行填充[2-3],合理增加矩阵稠密性,然后结合物品的上下文信息,得到用户偏好度矩阵,最后通过优化的皮尔逊相似度得到近邻用户,最终得到用户对物品的预测评分。
本文提出的基于Spark 的上下文感知算法是在Spark 平台进行计算的,主要通过缓解矩阵稀疏性、优化计算模型、提高算法可扩展性等方面对已投入应用的上下文感知推荐算法的优化,并在实际应用中对算法的可行性和准确性进行对比和分析。
1 相关算法设计
1.1 矩阵分解算法
矩阵分解算法是将高维矩阵分成两个低维矩阵,根据用户的评价矩阵对用户进行兴趣分析。假设用户的特征矩阵为U,包含个数M,物品的特征矩阵为V,包含个数为N,用户特征矩阵和物品特征矩阵的维度都是d。则所有用户对所有物品的评分构成的评分矩阵R 可表示为R=UTV。同样地,如果计算出U 和V 的值,也可反向推出R 的值,通过反向计算得到的用户物品评价矩阵与原矩阵近似。评分矩阵R 和近似矩阵之间的误差称为噪声,噪声值的分布属于高斯分布。
根据贝叶斯公式,得出噪声概率矩阵的概率密度函数为
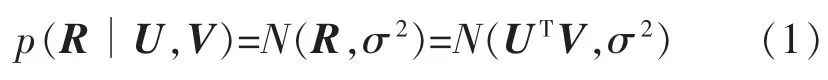
由贝叶斯后验概率可得:
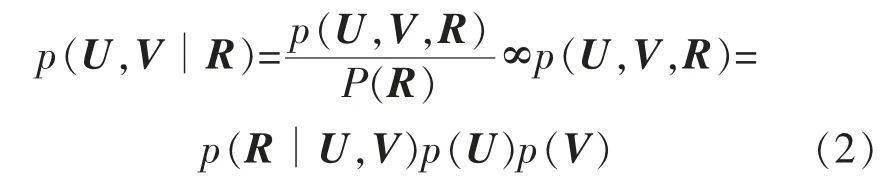
进行对数变换后,再求最大化后验概率,即求下式的最小值:
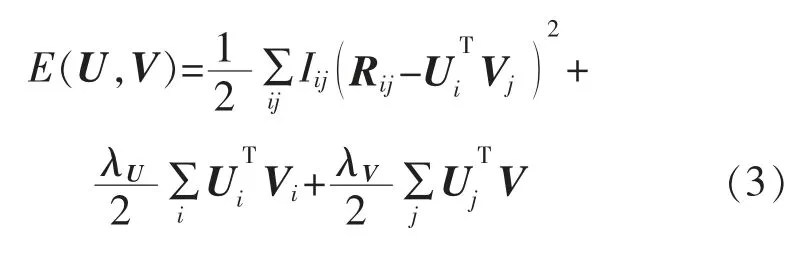
式中:

用梯度下降法多次迭代,直到求出最小值,最终将高维矩阵分解为维度较低的矩阵U 和矩阵V,同时根据低维矩阵也可得到原矩阵的相似矩阵。
在推荐系统中,为了缓解原始矩阵稀疏的问题会采用矩阵填充的方式。
一般情况下,采用将没有数值的位置填入统一度量的方式,如平均数、众数,或者根据实际应用场景人为设定一个较为合理的值,完善矩阵后再根据推荐算法得出推荐结果。这种方法对缓解稀疏性有一定的效果,但实际中大部分用户对该产品的评价与填充结果正好相反,导致通过算法计算后预测出的兴趣商品与用户的真实兴趣有很大误差[4-5]。
如果采用凸矩阵填充方式,即求矩阵迹或者迹模的最小化。这种方式计算结果比较理想,但是推荐系统中存储海量的用户和物品数据,使用这种方式需要将整个矩阵加载到内存中,会超出计算机的承受能力。
为了解决这些问题,本文引入非凸矩阵的填充。通过对非凸矩阵进行矩阵分解,将原始稀疏矩阵分解成两个维度较低的矩阵,在实际计算时只需存储分解后的两个低维矩阵,能够明显降低计算机的内存消耗。
1.2 相似度算法
在实际中,直接使用余弦相似度计算出的相似误差较大。根据用户的个性化评分尺度,同时统一评分标准,在计算时一般采用皮尔逊相似度。皮尔逊相似度公式为
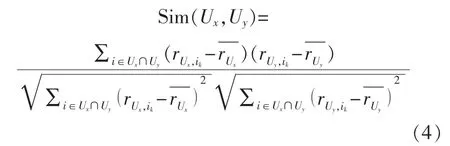
式中:rUx,ik是用户x 对物品k 的评分,是用户历史评价物品的平均分,用户y 同理。
商品i 是两用户历史记录中共同评价商品。
当用户访问的项目集合较小时,得到的结果会偏高。在计算相似度时可引入共同评分权重因子,可得相似度公式为
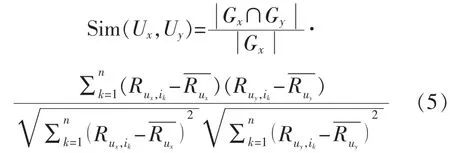
式中:Gx∩Gy为用户共同评价商品个数,Gx为目标用户评价商品总个数。
1.3 矩阵填充优化算法
为了最大化保留用户兴趣特征,提高矩阵填充的合理性,本文采用基于矩阵分解的矩阵填充方式。
(1)对用户对物品的原始评价矩阵R 进行矩阵分解,得到用户矩阵U 和物品矩阵V,并再次逆向计算得到相似矩阵。
(2)根据用户矩阵U 中任意两用户,得到用户对所有物品的评分向量c1和c2。
(3)根据向量c1和c2,判断物品矩阵中的某物品是否是两用户均未评价过的物品。若是,则不改变评价向量的值,若否,则根据相似矩阵中的评分对c1和c2进行填充,得到填充后的向量和和填充后的评价矩阵。
1.4 上下文感知算法
上下文信息可以描述某一事物相关状态的所有信息。在推荐系统中,算法的上下文感知信息可以有多种,大体可分为时间、地点、天气等物理信息,身份、社交对象等社会信息,年龄、心情、经验和认知能力等状态信息,推荐物品类型和属性等媒体信息。
根据推荐系统的数据集,可得到物品信息的上下文。设某个物品有k 个重要属性,则该物品的上下文信息总集合可定义为

式中:Ci是离散值,还可细分为子信息。
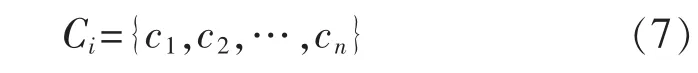
例如电影数据集,C={C1,C2},C1为主题,C2为年代,而主题又可分为爱情片、动作片和科幻片,年代可分为古代、现代和未来。在推荐系统中,可以根据用户信息以及所访问物品的上下文信息,得出用户对某类属性的访问次数以及访问项目总数,通过两者的比值,得出用户对某个特征类的偏好。

式中:Ni,c表示用户i 对属性c 的兴趣程度,Ci,c表示用户对属性c 的访问次数,Ii表示用户访问所有项目集合。
通过访问频率只能初步判断用户对某属性物品的兴趣程度,真正反映用户偏好特征的是用户对该属性物品的评分高低。
如果用户对某两个属性类的访问次数相同,但是对第一类属性中的物品评分普遍高于第二类属性,表示用户对第一类属性更有兴趣。

式中:Pi,c表示用户i 对属性c 评分程度,ri,c表示属性c 中评分高于用户评价平均分的物品数。
用户对某特征类的偏好程度为

1.5 基于Spark 的上下文感知推荐算法
根据上文提出的矩阵分解算法和上下文感知算法,本文提出了上下文感知优化算法。优化后的算法有效缓解了传统推荐算法[6]面临的原始矩阵稀疏问题,从优化相似度和转变计算工具的角度提高了推荐算法的准确性和效率性。
优化后的算法计算流程如下:
(1)原始矩阵填充:对原始的用户物品评价矩阵R 进行矩阵分解,计算出相似矩阵,并按照填充规则对原始矩阵进行填充。
(2)用户偏好相似度计算:计算用户对每个属性类在访问频率上的兴趣程度,形成用户属性兴趣矩阵。同时根据用户评价平均评分,形成用户主观评分矩阵。结合两矩阵形成用户偏好度矩阵Hi。
(3)将共同评价项目个数引入皮尔逊相似度,根据用户偏好度矩阵Hi得出目标用户与其他用户的相似度。
(4)根据相似度,找到与目标用户相似度最高的k 个用户,得到近邻用户集合Topk。
(5)根据相似用户集合中用户v 对项目的评分,预测目标用户的项目的评分。选取评分最高的项目推荐给用户。评分公式为

考虑到每个人的评分尺度差别,在计算预测评分时减去用户的平均评分。
在推荐算法中,优化各流程中的参数可以使推荐结果的准确度得到提高,但同时也增加了计算量。矩阵填充和相似度的计算增加了多个计算环节,这些额外的步骤会增加计算时长。面对大数据时代的海量数据,算法优化带来的额外耗时是无法预判的。为了增加算法的拓展性,引入了大数据分布式计算平台—Spark。
Spark 是大规模数据处理的通用计算引擎,随着近几年的发展已经形成了功能完善的分布式计算系统。它基于弹性分布式数据集RDD 的转化实现对数据的计算,计算时Spark 将数据加载到内存,执行效率非常高。
根据推荐算法的拓展性和效率性要求,可以将算法部署在Spark 平台,计算时多个算法并行执行。每个计算环节都通过多台服务器分布式处理,从而极大地提高算法的执行效率。图1 展示了系统对于关键用户推荐的整体流程。
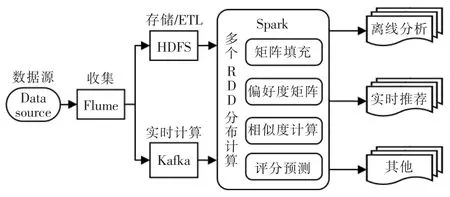
图1 Spark 进行用户推荐整体流程Fig.1 Process of user recommendation on Spark
2 实验结果分析
针对传统推荐算法本身的局限性,本文通过对矩阵填充、结合上下文感知信息和完善计算工具等方式完善推荐算法,最终使推荐算法更准确的反映用户的实际需求。为了更好地验证推荐结果的准确性,本文用音乐数据集中的数据检验优化后的算法在准确度和效率上的提高。
2.1 实验数据来源
考虑到优化后的算法会涉及上下文信息、矩阵填充等因素,用Last.fm 提供的音乐数据集hetrec 2011-lastfm-2k 来进行算法的性能和结果准确度的验证。
在Last.fm 音乐集中,包含每个用户和最受用户欢迎的艺术家列表以及播放次数。它还包括可用于构建内容向量的用户应用标签,是具有用户社交网络信息的数据集。在数据集中,用户作为算法中的样本用户,艺术家作为算法中被推荐的项目,用户收听数作为样本用户的评分数据,标签数和标签记录数作为考察项目关系的标准。音乐数据集总体信息见表1。

表1 音乐数据集总体信息Tab.1 General music dataset information
Last.fm 数据集的稀疏度为
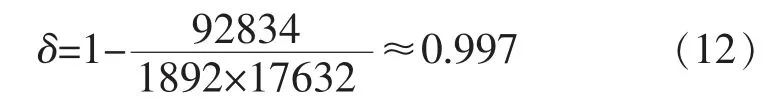
在结果测试时,选取最新12 个月的数据,训练集和测试集各自占比为80%和20%。
2.2 评价指标
衡量算法性能有多种评价指标: 如准确度、覆盖率、扩展性等。其中,算法准确度包括分类准确度和误差度。误差度包括平均绝对误差MAE 和均方根误差RMSE。计算MAE 的过程非常直观,直接计算最终的推荐结果和用户记录的真实值的差别。MAE 值越小,意味着推荐算法预测的值更接近用户的真实兴趣,推荐准确度就越高。计算公式为
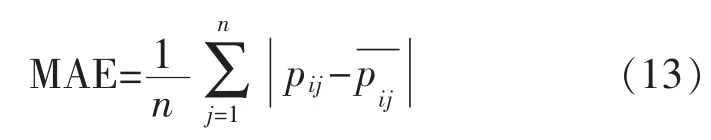
式中:n 为样本个数;pij为用户的真实评分;为预测评分。
2.3 实验结果分析
2.3.1 矩阵稀疏度分析
为了解决初始矩阵稀疏影响推荐算法计算准确率的问题,优化后的算法对原始用户物品评价矩阵进行了填充。在实验中,随机抽取数据集中的数据作为初始用户评价矩阵,记为matrix-init,然后根据上述填充算法对初始矩阵进行填充,新生成的矩阵记为matrix-fill。将填充前后的2 个矩阵进行稀疏度的对比,稀疏度用矩阵中空缺值的个数与矩阵中总元素的比值表示。
在数据集中随机选取不同数量的用户进行矩阵填充,填充前后的稀疏度对比结果如图2 所示。

图2 矩阵填充前后稀疏度对比Fig.2 Comparison of sparsity before and after matrix filling
从填充结果来看,填充后矩阵的稠密性有明显的增加,填充后的矩阵的稀疏度远远小于原始矩阵的稀疏度。从稀疏度的变化趋势来看,随着用户数的增加,原始矩阵的稀疏度变化不大,但是填充后的矩阵稀疏度有增加的趋势。因为随着用户和物品的增多,用户评价过的物品占总物品比例降低,矩阵填充总数量降低。
2.3.2 准确度分析
对于推荐算法而言,评价算法是否得到优化的一个重要标准就是准确度。在对比推荐算法的准确度实验中,通过对近邻用户数的控制来观察不同推荐算法下平均绝对误差MAE 值的变化。MAE 值越低,则推荐算法的结果准确度越高,表明改进后的算法有更高的应用价值。
在实验中,测试样本集数据随机抽取总用户个数为1000,音乐家个数为3000,将近邻函数个数作为自变量。为了验证改进后的模糊聚类算法对上下文感知算法准确度的有所提高,实验将基于基础上下文感知和优化后的算法的MAE 值和执行时长进行了对比。
实验时,将基于用户的基础上下文感知算法记为CF-base,将进行过初始矩阵填充步骤然后使用基础上下文感知计算的算法记为CF-fill,将本文提出的上下文感知算法记为CF-context。计算相似度时采用结合用户共同评价物品的皮尔逊相似度计算目标用户的近邻用户。
三种算法下,根据近邻用户数的不同,得出的MAE 值的变化结果如图3 所示。
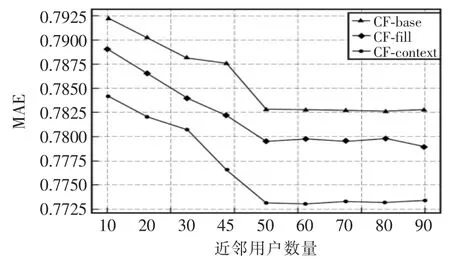
图3 三种算法下近邻用户数对MAE 值的影响Fig.3 Influence of the number of neighbor users on the MAE value under the three algorithms
从图3 可以看出,三种算法下的平均绝对误差随着近邻用户的增加逐渐降低直至平稳收敛到某值而不再改变。
从总体上来看,CF-fill 算法和CF-context 算法推荐结果的准确率比CF-base 算法更高。在相同条件下,CF-fill 算法比CF-base 算法的MAE 值更小,说明对初始矩阵进行填充对推荐结果准确性的提高是有效果的。
在近邻用户个数在50 时,各算法的MAE 值趋于最佳状态。随着近邻用户个数的持续增加,误差不再持续降低,反而有上升趋势,由此看出近邻用户过多也会对最终推荐结果的准确性造成干扰。
2.3.3 算法执行效率分析
固定近邻用户为50 时,设置定时任务记录算法的执行时间如表2。

表2 算法执行时间对比表Tab.2 Algorithm execution time comparison
从计算时间上看,执行三种算法所需的时间差距不大,CF-context 算法需要时间相对较长。对算法进行优化后,会增加额外的计算环节,需要更长的时间得出推荐结果。虽然计算时长有所增加,但是增加的幅度不大,而且推荐结果的准确度有明显的提高,因此CF-context 算法有更高的使用价值。
3 结语
传统的推荐算法由于原始矩阵稀疏和实际场景等约束条件的存在,得出的推荐结果可能与用户真实的兴趣项目差距较大。
本文在传统算法的基础上,提出了基于Spark的上下文感知推荐算法,在矩阵稀疏性、用户和物品属性、计算平台等方面进行了优化,在计算时长增加幅度可接受范围内,提高了推荐算法的准确度,进一步提高了推荐算法在实际场景下的适用性。

