基于卷积神经网络的红外与可见光图像融合

董安勇，杜庆治，苏 斌，赵文博，于 闻

（1.昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2.昆明北方红外技术股份有限公司，云南 昆明 650500）

0 引言

红外成像传感器具有捕捉物体热辐射的能力，但对场景纹理细节信息的变化不具有敏感性。可见光成像传感器具有捕捉场景空间细节信息的能力，但容易遭受周围恶劣环境的影响。因此，融合红外与可见光图像可以捕捉各波段互补特征，显示辐射目标保留场景信息。目前，在情报收集、监控安全以及航空航天等领域有广泛的应用前景。

非下采样剪切波变换（non-subsampled shearlet transform,NSST）具有平移不变特性和稀疏表示能力，在图像融合领域已经成为众多学者研究的热点。文献[1]提出了稀疏表示和非下采样Shearlet 变换相结合的多聚焦图像融合算法，该算法可以使用融合的低频子图构造过完备字典，捕捉源图像更多的边缘、纹理以及细节信息。文献[2]提出了NSST与引导滤波相结合的多聚焦图像融合算法，该算法设计了基于局部区域显著性特征的引导滤波加权融合模式，可以保留源图像较多的对比度和清晰度信息。但是，上述算法的融合模式都是人为给定的，缺乏自适应调节的能力。

卷积神经网络（convolution alneuraln et work,CNN）可以将数据特征进行分层表示，从而有效地挖掘数据局部和全局的特征信息，可以克服现有算法缺乏学习自我特征能力的缺陷。文献[3]提出了基于卷积神经网络的红外与可见光图像融合算法，该算法使用卷积神经网络得到了衡量源图像特征信息的决策图来自适应调整融合模式。文献[4]提出了基于图像分割的卷积神经网络多聚焦图像融合算法，该算法通过卷积神经网络将源图像进行分割来输出对应的决策图。但是，上述算法没有从多尺度角度将源图像划分为高低频子带进行处理，不符合人眼视觉系统的特性。

脉冲耦合神经网络（pulsecoupled neural network,P CNN）模型具有全局耦合和脉冲同步的特性，可以将变换域高频子带融入丰富的视觉特性信息。文献[5]提出了基于自适应PCNN模型的四元数小波域图像融合算法，该算法使用拉普拉斯算子优化PCNN模型的阈值，改善了融合图像的视觉效果。但是，该算法未能解决人工设定自由参数的困难，不利于自适应地调整网络参数。文献[6]提出参数自动设置的简易P CNN模型，该模型可以根据图像的特征信息自适应地设置PCNN 模型的自由参数，具有较强的适用性。

针对上述问题分析，本文综合NSST 变换、CNN（convolutional neuraln et work）模型以及PCNN模型的互补特性，提出了基于深度卷积神经网络的红外与可见光图像融合算法（NSST-CNN-APCNN（Adaptive Pulse Coupled Neural Network,APCNN）算法）。该算法从变换域角度解决了低频子带不具有融合模式自适应调整的能力，同时又避免了经典简易PCNN模型手动设置自由参数的困难，增强了算法的表现力，优化了融合处理过程，具有较高的适用性。

1 NSST变换与PCNN模型

1.1 非下采样剪切波变换

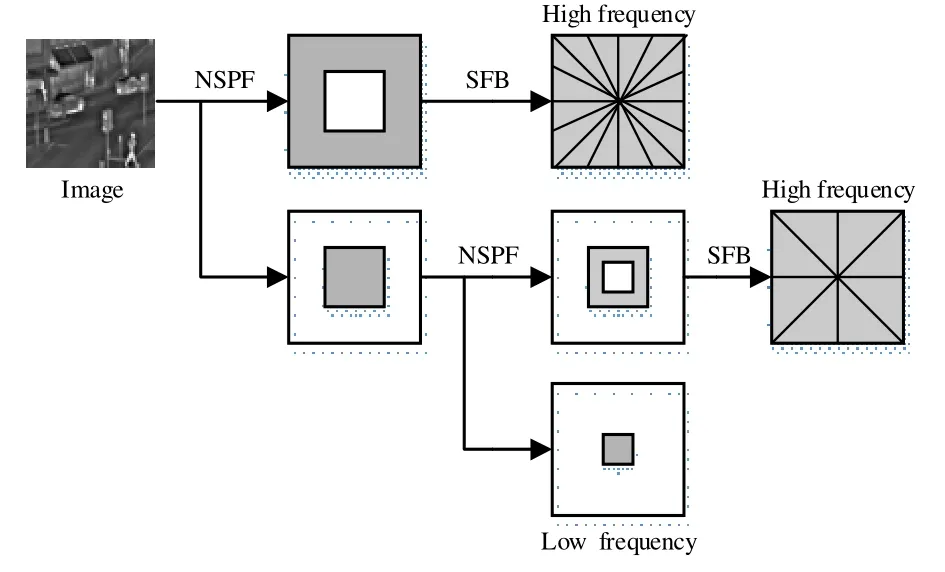
图1 NSST 变换过程Fig.1 NSST trans formation process

NSST变换主要包括两个处理过程，即多尺度分解和方向局部化。多尺度分解过程是使用金字塔滤波器（non-subsam pledpyra midfilter,NSPF）将源图像分解成k＋1个子带（1个低频分量和k个高频分量）。方向局部化过程使用剪切波滤波器将高频分量进行j级方向变换，可以得到2j个高频分量，很大程度上克服了伪吉布斯效应[7]。“store”图像2级NSST 变换过程如图1所示，分解的部分子带如图2所示（其中，(a)为低频子带，(b)和(c)为高频子带）。

图2 NSST 分解子带Fig.2 NSST deco mpositionsubb and

1.2 参数自适应脉冲耦合神经网络

为了解决经典PCNN模型需要人为设置自由参数的问题[8-9]，本文选用了参考文献[10]提出的参数自适应脉冲耦合神经网络（简称为APCNN模型）。APCNN模型的数学描述如式(1)：

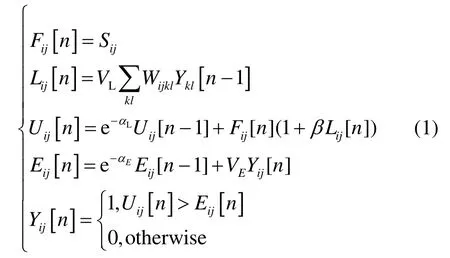
在上述APCNN 模型中，Fij[n]、Lij[n]、Uij[n]以及Eij[n]分别为(i,j)坐标神经元迭代n次的反馈输入、链接输入、内部活动以及动态阈值。VL和αL分别为链接输入的幅度系数和时间常数。VE和αE分别为变阈值函数的幅度系数和时间常数。Sij、β以及Wijkl分别为输入激励、链接强度以及突触连接系数。从APCNN 模型中可以看出，存在VL、VE、αL、αE以及β5 个自由参数。其中，VL和β仅为的权重。因此，设λ＝βVL表示加权链接强度，将APCNN模型用来处理图像融合问题，可以自适应地给出剩余4 个自由参数的数学描述：

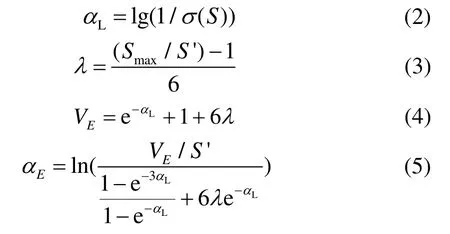
式中：σ(S)为输入图像的标准偏差；S′和Smax分别表示归一化阈值和输入图像的最大强度。

2 卷积神经网络

卷积神经网络可以利用高维空间关系来解决人为设定特征信息的问题，从而具有很强的特征学习和特征提取能力。CNN 模型主要由输入层、卷积层、池化层、全连接层以及输出层组成[11]，CNN 模型的基本结构如图3 所示。其中，卷积层是模型的核心部分，主要作用是提取数据特征。每个卷积核都可以提取上一层输入数据的特征，且随着卷积核数量的不同，提取的特征丰富度也不同。池化层位于卷积层之后，主要作用是为了优化参数规模、降低空间容量以及减少过拟合的影响。全连接层位于模型的末端，类似于人工模型的全连接方式。另外，如果需要解决分类问题，可以依次连接分类层。

对于基于CNN 模型的图像融合算法来说，图像融合的处理转变成了CNN 模型的设计，融合模式可以通过训练CNN 模型自动生成。同时，学习的特征数据可以被视为“最优”方案。因此，基于CNN 模型的融合算法可以有效地解决需要人为设定自由参数的难题。为了保证两幅源图像特征提取和信息量估计的处理方式是一致的，本文选用了参考文献[12]设计的孪生双通道神经网络（siamese convolution neural network, SCNN）。SCNN 模型可以通过双通道的CNN特征学习将双通道输入图像的匹配度进行估计，并由分类器输出图像匹配的结果，具有较高的收敛性。

3 基于NSST-CNN-APCNN 的红外与可见光图像融合算法

NSST-CNN-APCNN 算法首先将红外与可见光图像进行4 级NSST 分解得到具有结构特征的低频子带和保留细节特征的高频子带。然后，将NSST 域低频子带输送到孪生双通道CNN 模型，经过CNN 模型的特征学习和分类来评估出决策图，再根据决策图输出概率值和局部相似性测量函数，判别出可以自适应调整的融合模式来完成NSST 域低频子带的融合。其次，使用NSST 域高频子带的绝对值作为APCNN 模型的激励输入，同时分别使用方差、区域能量以及可见度特征信息来调节式(2)中σ(S)的值。因此，可以根据输入特征自适应地调整APCNN 模型的自由参数，从而输出点火映射图来完成NSST 域高频子带的融合。最后，通过使用NSST 逆变换将红外与可见光融合图像进行重构。基于NSST-CNN-APCNN 的红外与可见光图像融合算法框架如图4 所示。

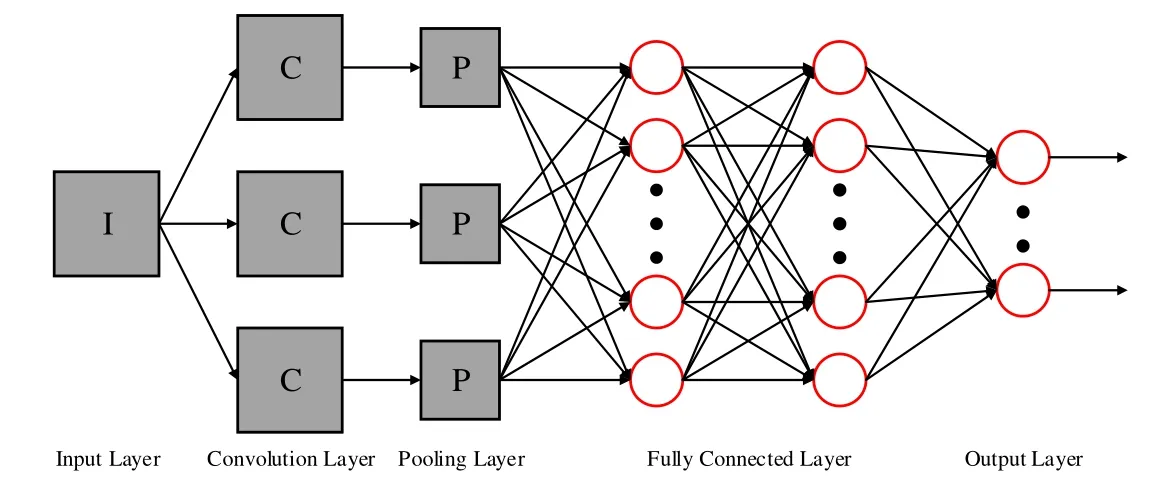
图3 CNN 模型基本结构Fig.3 Basic structure of the CNN model

3.1 基于SCNN 模型的低频系数融合

NSST 域低频子带系数融合决策图的生成可以被认为是分类问题的处理。具体来说，可以通过测量图像块信息量的多少得到系数融合的决策图。SCNN 模型的网络结构具有相同权重和相同体系的两个输入分支，因此SCNN 模型对于两个输入图像块的特征提取和信息估计方式是一致的，且容易被数据集训练，具有较好的收敛性。本文选用的SCNN 模型基本结构如图5 所示。

本文算法将NSST 域低频子带分别输送到SCNN模型的两个分支，通过3 个卷积层和一个最大池化层可以得到两个衡量图像块信息量的特征映射。两个特征映射通过神经元数目分别为256 和2 的两个全连接层实现决策分配可以得到最终的概率值决策图。其中，神经元数目为2 的全连接层是分类层，神经元数目2 为分类类别，通过分类器Softmax 可以输出分类的概率值。这样，SCNN 模型输出的决策图决定了对应位置处源图像块细节信息的多少。为了使人类视觉神经系统获得更好的感知效果，本文算法首先将NSST域低频子带进行了拉普拉斯分解，然后将SCNN模型输出的决策图进行了高斯滤波分解，最后在每个分解层级上完成NSST 域低频子带系数的融合。NSST域低频子带系数融合的基本框架如图6 所示，具体的融合流程如下所示。

图4 基于NSST-CNN-APCNN 的图像融合框架Fig.4 Image fusion framework based on NSST-CNN-APCNN

图5 SCNN 模型基本结构Fig.5 Basic structure of SCNN model

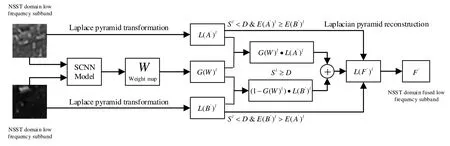
图6 低频子带系数融合基本框架Fig.6 Basic framework for the fusion of low-frequency subband coefficients

步骤1：将大小为256×256 的红外低频子图AL和可见光低频子图BL分成大小为16×16 的图像块集，成对地输送到预先训练的SCNN 模型。

步骤2：将SCNN 模型两个分支输出的256 个特征映射级联，再与256 维特征向量完全连接可以得到特征映射图。

步骤3：将步骤2 得到的特征映射图重叠区域块“求平均”，从而得到与源图像具有相同尺寸的特征映射图。

步骤4：将步骤3 得到的特征映射图中概率值大于0.5 的视为细节信息特征，置为1；小于0.5 的，视为非细节特征信息，置为0。

步骤5：将步骤4 得到的特征映射图输入到Softmax 分类器，并重新按照顺序拼接可以得到二值图。

步骤6：将步骤5 得到的二值图进行滤波处理，得到NSST 域低频子图系数融合最终的决策图W。

步骤7：将成对输入的图像块AL′和BL′进行拉普拉斯分解，分别得到L(AL′)l子带和L(BL′)l。其中，l为拉普拉斯分解层级。

步骤8：将步骤6 得到的决策图W进行高斯滤波处理，得到W分解子带G(W)l。其中，步骤7 和步骤8 的分解级数设置为w和h分别为源图像块的空间大小，为向下取整。

步骤9：根据式(6)分别完成L(AL′)l子带和L(BL′)l子带的局部区域能量E(AL′)l(x,y)和E(BL′)l(x,y)的计算：

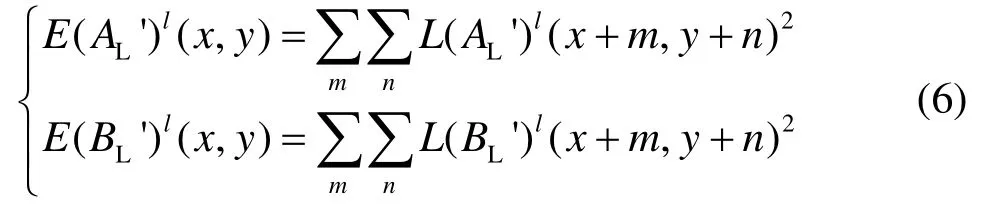
步骤10：设计了基于局部相似性的测量函数Sl(x,y)。其中，Sl(x,y)的函数值范围为[－1,1]，设置阈值D来自适应地调整融合模式。Sl(x,y)测量函数如式(7)表示：

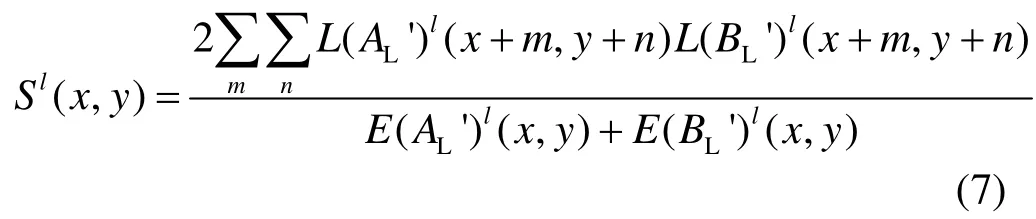
步骤11：当相似性较大时，SCNN 模型提取的特征信息是可靠的，此时可以根据SCNN 模型输出的决策图进行低频系数融合：

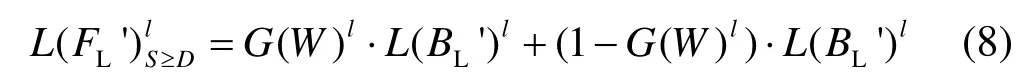
步骤12：相似性较低时，决策图W是不可靠的，此时应该选择局部区域能量较大者，式(9)为具体的融合模式：

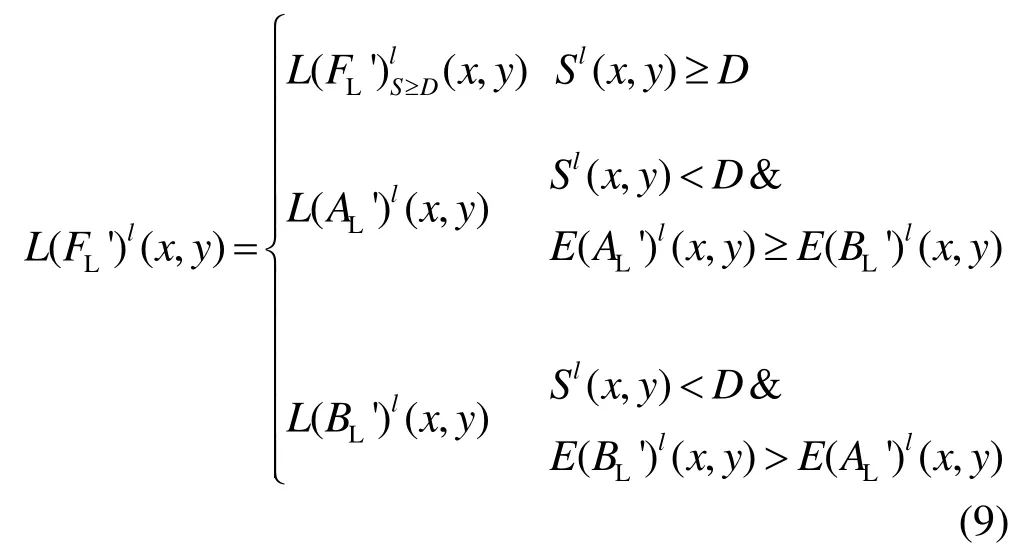
步骤13：将融合的低频子带L(FL′)l(x,y)进行拉普拉斯逆变换，可以得到融合的NSST 域低频子图。

3.2 基于APCNN 模型的高频系数融合

经典的高频子带融合模式不能够充分利用高频细节特征，不仅容易导致图像的结构和空间信息大量丢失，而且容易引入噪声和忽略细节。

因此，本文算法克服了需要人为设置PCNN 模型自由参数的难题[13]，根据红外和可见光图像类型的特征分别选用了子带的标准偏差、局部区域能量和以及局部区域可见度信息自适应地设置网络参数来估计NSST 域高频子带系数的细节强度，可以有效地保留高频子带的显著特征信息，符合人类的视觉神经感知。

对于基于PCNN 模型的融合模式，通常选用单个像素的灰度值来激励PCNN 模型。但是，人类的视觉系统对单个像素是不敏感的，因此本文算法选用整个高频子图的绝对值来激励APCNN 模型，即：

链接强度β可以改变链接通道权重来决定邻域神经元的内部活动状态，通常是通过实验来确定β值。但是根据人眼视觉系统原理，神经元的β值是随着周围特性的变化而变化的，因此β值需要随着高频子图的特征来自适应地调节。根据1.2 节APCNN 的设计，设λ＝βVL，则αL、λ、VE以及αe可以分别由式(2)、式(3)、式(4)以及式(5)表示。

式(2)的σ(S)为输入图像的标准偏差。但是，对于红外与可见光图像类型，局部区域能量和与局部区域可见光越大，表示视觉显著性区域包含了较多的边缘、轮廓以及纹理特征。因此，设σ(S)分别为局部区域能量和EOL、局部区域可见度VI 以及标准偏差SD来自适应地调节APCNN 模型的自由参数，捕捉NSST域高频子图更多的特征信息，即：

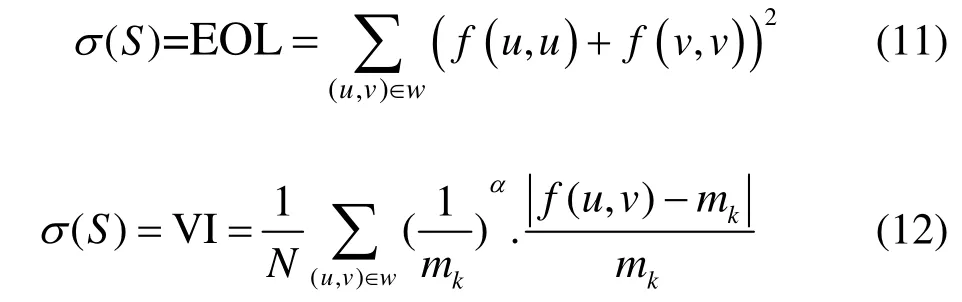
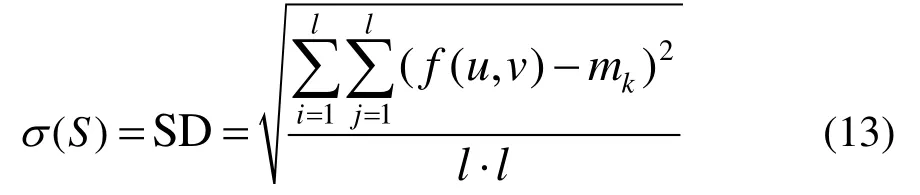
式中：f(u,v)表示(u,v)处的像素值；w表示尺寸为l×l的窗口；mk表示像素平均值；N表示窗口像素数；α表示常数。

NSST 域高频子带系数融合的具体流程如下所示：

步骤1：分别计算出NSST 域红外高频子图AH和可见光高频子图BH的绝对值AHa和BHa。

步骤2：将绝对值AHa和BHa分别归一化处理，赋值给Fij激励APCNN 模型。

步骤3：将APCNN 模型进行参数初始化，即：

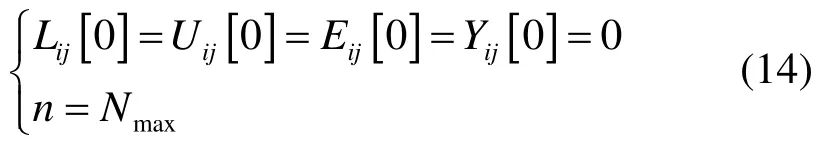
步骤4：设定EOL、VI 以及SD 特征分别为σ(S)。

根据公式(2)～(5)分别计算出APCNN 模型自适应参数。

步骤5：根据APCNN 模型的运行机制，实现Nmax次迭代，EOL、VI 以及SD 特征调参的点火次数分别为：TAE[Nmax]、TAV[Nmax]、TAS[Nmax]、TBE[Nmax]、TBV[Nmax]以及TBS[Nmax]。

步骤6：根据显著性特征调参的点火输出，构造加权函数：

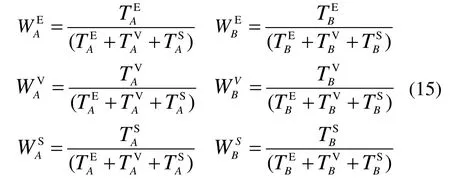
步骤7：根据步骤6 设计的加权函数，构造红外高频子图AH和可见光高频子图BH的点火映射图：

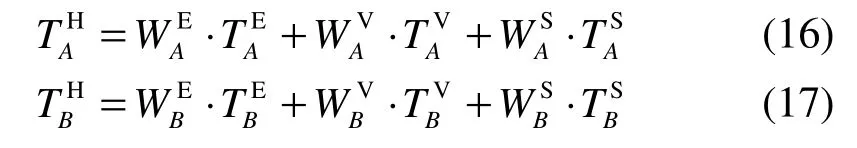
步骤8：根据新点火图，得到融合的高频系数：

4 实验结果与分析

4.1 实验说明

为了验证NSST-CNN-APCNN 算法的实用性，选用了大小为256×256 预配准的“森林”（场景复杂，而目标单一）、“船”（场景单一，而目标复杂）以及“商店”（场景复杂，且目标复杂）3 组红外与可见光图像进行融合实验，并将NSST-CNN-APCNN 算法与较为先进的5 种融合算法进行性能比较，对比算法分别为：文献[14]（简称NSCT-PCNN 算法）、文献[15]（简称SR 算法）、文献[16]（简称NSST 算法）、文献[17]（简称NSST-PAPCNN 算法）以及文献[18]（简称CNN 算法）。其中，仿真环境为2016b MATLAB，各组源图像均进行“归一化”处理，对于NSST 变换部分，均选用“maxflat”滤波器，分解级数为4，方向子带为[8,8,16,16]（其他参数根据文献设定）。

4.2 融合评价

图像融合质量评价方法主要有两个方面，即主观视觉评价和客观指标评价。为了可以更加客观地评价NSST-CNN-APCNN 算法的性能，选用了空间频率（SF）、清晰度（SP）、边缘信息传递因子（QAB/F）、结构相似模型（SSIM）以及视觉信息保真度[19]（VIFF）5 个评价指标评估融合图像的融合质量（指标值越大，融合质量越高，融合效果越好）。

第一组“森林”图像实验素材如图7(a)～(b)所示，图7(a)是可见光灰度图像，图7(b)是与之对应的红外图像。而图7(c)～(h)是不同算法对图7(a)～(b)进行图像融合得到的融合结果灰度图像。

从图7(c)～(h)融合结果可以看出，上述融合算法均可以有效地将源图像的互补信息进行融合，既显示了目标，又刻画了场景。但是，不同的融合算法捕捉特征信息的能力也是各不相同的。NSCT-PCNN 算法的实验结果中，护栏纹理清晰，但树木出现“重影”现象。SR 算法的实验结果中，目标和场景层次感增强，但对比度严重减弱。NSST 算法和NSST-PAPCNN算法的实验结果中，目标人物清晰，但纹理信息丢失严重。CNN 算法的实验结果中，灰度层次感较强，但屋檐左侧的树木存在空间“不连续”现象。NSST -CNN-APCNN 算法的实验结果中，目标和场景对比度增强，纹理结构特征明显，保留了源图像较多的细节信息。

第一组“森林”图像的客观质量评价指标如表1所示，评价指标值归一化走势如图8 所示。

从表1 的客观质量评价指标可以看出，NSST -CNN-APCNN 算法的QAB/F指标略低于CNN 算法，但SF、SP、VIFF 以及SSIM 指标均明显优于5 种对比算法。从图8 的归一化走势可以看出，虽然NSST -CNN-APCNN 算法的QAB/F指标略低，但是VIFF 指标相比于SR 算法提高了约28.62%，具有较好的视觉保真度。综上可知，NSST-CNN-APCNN 算法捕捉边缘信息的能力略弱于CNN 算法，但在活跃度、清晰度、保真度以及结构信息方面的保留能力优于5种对比算法，具有较优的融合性能。

第二组“船”图像实验素材如图9(a)～(b)所示，

图7 “森林”图像不同算法的融合结果Fig.7 Fusion resultsof different algorithms for "forest"images

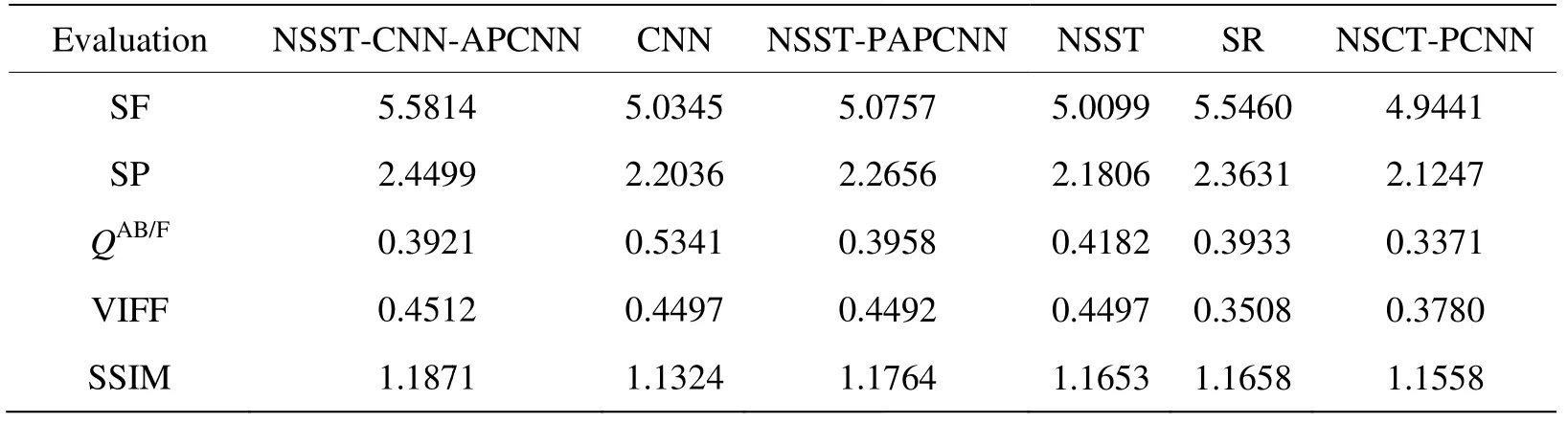
表1 “森林”客观质量评价指标Table 1 “forest”objective qualityevaluation indicators

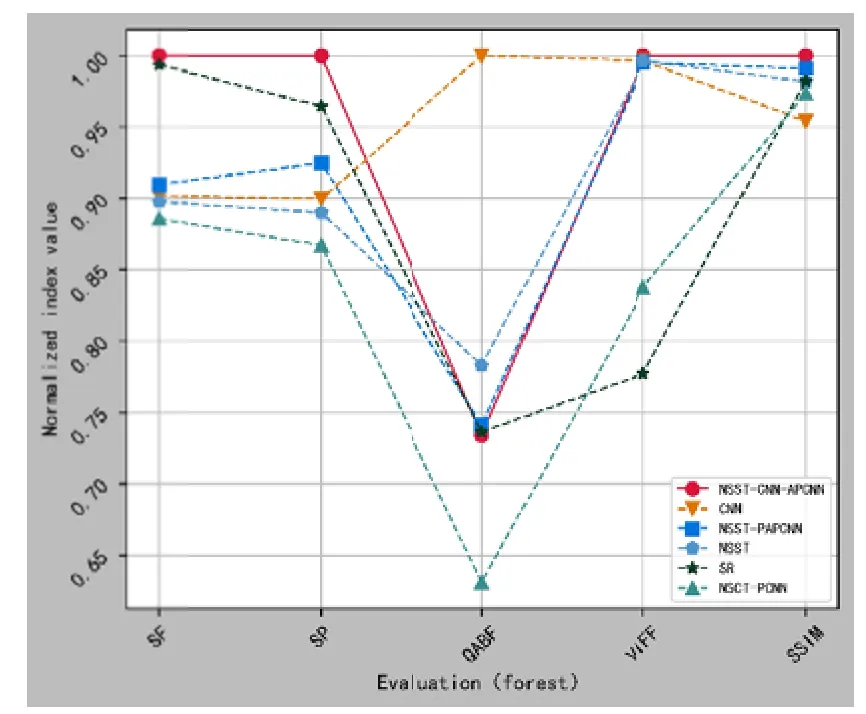
图8 “森林”指标值归一化走势图Fig.8 “forest”indicator valuenormalization chart

从表2的客观质量评价指标可以看出，NSST 图9(a)是可见光灰度图像，图9(b)是与之对应的红外图像。而图9(c)～(h)是不同算法对图9(a)～(b)进行图像融合得到的融合结果灰度图像。-CNN-APCNN算法的SSIM指标略弱于SR 算法，说明其空间结构特征信息的捕捉能力弱于SR 算法。但是，NSST-CNN-APCNN算法的其他客观质量评价指标均明显优于5种对比算法，可以提高观察者对目标和场景的感知能力，有助于目标跟踪和检测识别的实际应用。从图10的归一化走势可以看出，NSST-CNN-APCNN算法、CNN算法以及NSST-PAPCNN算法的走势略为一致，NSST 算法、SR 算法以及NSCT-PCNN算法的走势略为一致，且前三者的VIFF指标明显高于后三者，刻画了源图像更深层面的保真度和结构特征信息。另外，NSST-CNN-APCNN 算法除了SSIM指标，其他客观质量评价指标均为“最优值”，且VIFF指标相比于NSCT-PCNN算法提高了约71.44%，融合效果高度符合人眼视觉效果。

第3组“商店”图像实验素材如图11(a)～(b)所示，图11(a)是可见光灰度图像，图11(b)是与之对应的红外图像。而图11(c)～(h)是不同算法对图11(a)～(b)进行图像融合得到的融合结果灰度图像。

图9 “船”图像不同算法的融合结果Fig.9 Fusion results of different algorithms for “boat”images

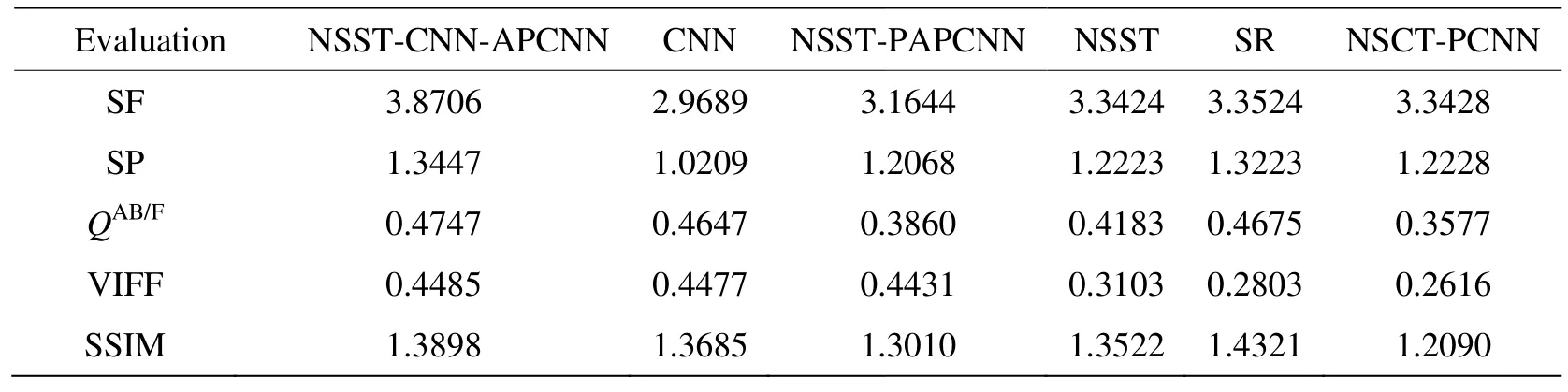
表2 “船”客观质量评价指标Table 2 “forest”objective quality evaluation indicators

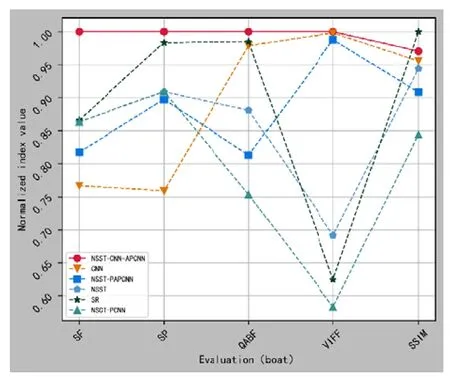
图10 “船”指标值归一化走势图Fig.10 “boat”indicator valuenormalization chart

从图11(c)～(h)融合结果可以看出，NSCT-PCNN算法的实验结果中，物体边缘轮廓模糊，丢失了部分亮度信息，分辨率较差。SR 算法的实验结果中，目标和场景纹理清晰，但亮度信息丢失明显。NSST算法的实验结果中，物体边缘过度平滑，且出现了重影干扰。CNN 算法的实验结果中，几乎丢失了全部的可见光信息，不适合用于目标复杂且场景复杂类型的图像融合。NSST-PAPCNN算法和NSST-CNN-APCNN算法的实验结果中，物体连续性较好，细节刻画深刻，且灰度、亮度以及锐利度比较贴近源图像。但是，NSST-PAPCNN算法的目标均存在“虚影”和“重影”的现象，使得人眼甄别困难。因此，NSST-CNN-APCNN算法的融合结果可以更好地分配可见光和红外信息，有效地消除了“伪影”，保留了较好的细节信息。

第3组“商店”图像的客观质量评价指标如表3所示，评价指标值归一化走势如图12所示。

图11 “商店”图像不同算法的融合结果Fig.11 Fusion results of different algorith msfor "store "images

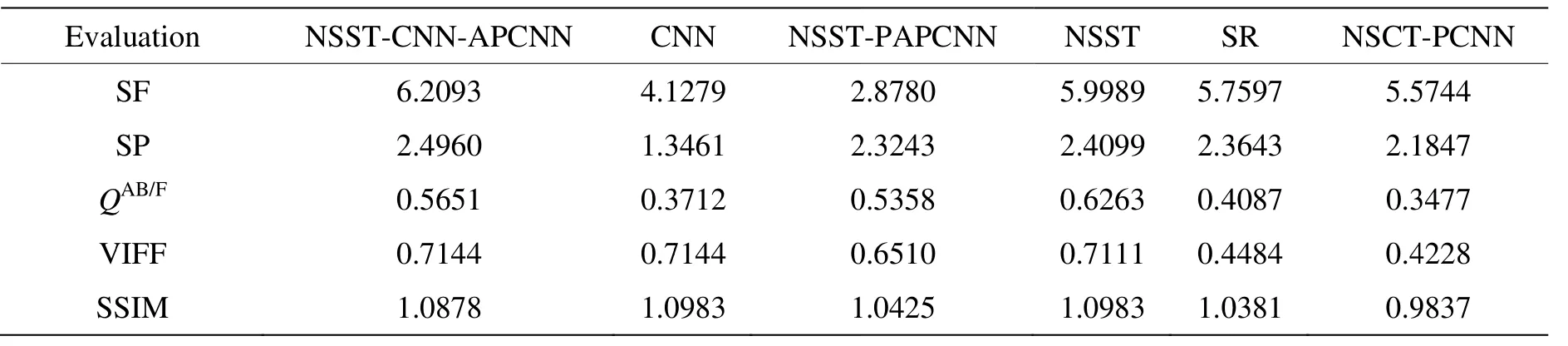
表3 “商店”客观质量评价指标Table 3 “Store” objective q ualityevaluation indicators

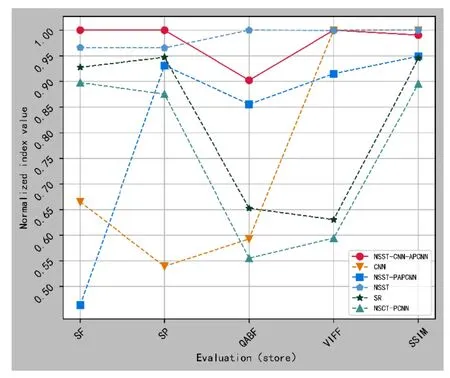
图12 “商店”指标值归一化走势Fig.12 “Store”indicator value normalization chart

从表3的客观质量评价指标可以看出，NSST -CNN-APCNN 算法的QAB/F指标和SSIM指标略弱于NSST 算法和CNN算法，说明NSST-CNN-APCNN算法遗失了少数的边缘细节信息和深度结构特征。但是，NSST-CNN-APCNN算法的SF、SP 以及VIFF指标依旧明显优于5种对比算法，能够较好地改善图像的分辨率、增强图像的清晰度以及提高图像的保真度。从图12的归一化走势可以看出，NSST-CNN-APCNN 算法和NSST 算法的各项客观评价指标均明显优于其他4种对比算法。另外，NSST-CNN-APCNN 算法在QAB/F指标和SSIM 指标略弱于NSST算法，但从图11(e)中可以看出，NSST算法的融合效果存在“振铃效应”，从主观视觉评价和客观指标评价综合分析来看，NSST-CNN-APCNN算法捕捉了更多的清晰度、相似性以及边缘纹理等细节信息，具有较好的可识别度。

5 结束语

NSST-CNN-APCNN算法将NSST变换、卷积神经网络以及参数自适应的PCNN 神经元模型相互结合，解决了NSST 分解低频子带融合模式给定的问题，同时又避免了手动设置脉冲耦合神经网络（PCNN）参数的困难。为了提取到源图像更加丰富的信息，NSST-CNN-APCNN 算法对于NSST 分解的低频和高频系数分别进行了更加细致的处理，其将低频子带进行了拉普拉斯分解，将SCNN 模型输出的决策图进行了高斯滤波分解，最终在每个分解层级上完成了低频系数的融合。对于高频子带的融合，其分别使用了方差、局部区域能量以及可见度特征来激励参数自适应PCNN 神经元模型。综合分析实验结果可知，在主观和客观评价方面，NSST-CNN-APCNN 算法均取得了较好的融合结果，较好地低刻画了源图像的结构、纹理以及相似性等特征，有效地抑制了“伪影”和“失真”状况的出现，并且在“森林”图像实验中，融合图像的SF 指标、SP 指标、VIFF 指标以及SSIM 指标相比于对比算法中最高的分别提高了约0.64%、3.67%、0.33%以及0.91%。在“船”图像实验中，融合图像的SF 指标、SP 指标、QAB/F指标、VIFF 指标以及SSIM 指标相比于对比算法中最高的分别提高了约15.26%、1.69%、1.54%、0.18%以及1.56%。在“商店”图像实验中，融合图像的SF 指标和SP 指标相比于对比算法中最高的分别提高了约3.51%和3.57%。且VIFF 指标和最高的指标一样。综上可以看出，NSST-CNN-APCNN 算法可以在保证其他指标减少较少的情况下提高图像的SF 指标、SP 指标以及VIFF指标，具有刻画源图像更深层面几何结构的能力。