航天器柔性太阳翼最优PPF主动振动抑制方法

鄂 斌，杨志红，崔乃刚，王小刚

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001；2. 中国航天科工飞航技术研究院，北京 100074)

0 引 言

轻质化、柔性化是现代航天器结构设计的发展趋势之一，然而这种设计会使得结构的低频模态分布较为聚集，在受到空间外部扰动等作用[1]或者进行姿态机动时容易发生振动。同时，柔性航天器自身的结构阻尼小，振动发生后并不能快速衰减，特别是在有诸多低频模态存在的情况下，振动持续时间过长的问题会尤为明显。长时间的持续振动对其上精密元器件的正常工作和空间任务普遍的高精度指向等需求而言都是十分不利的。

针对柔性航天器结构的振动控制问题，学者们提出了多种主动振动控制方法[2-4]。由于压电陶瓷材料具有响应速度快、重量轻和能源消耗低等特点，压电陶瓷元件被广泛地作为执行器应用于空间航天器的主动振动控制[5]。然而，使用压电陶瓷元件作为执行器进行主动振动控制时会发生控制溢出问题[6]。另一种能够广泛应用于柔性航天器主动振动并具有突出优点的执行器是角动量交换装置，它能够在仅占用较小内部空间的条件下，提供足够大的控制力矩。

针对带有角动量装置的柔性体结构构型，D’Eleuterio和Hughes[7-8]研究了具有连续分布的陀螺特性的固定边界柔性结构，基于线弹性假设推导了描述该系统运动特性的偏微分动力学方程，并首次提出了陀螺柔性体的概念。然而，他们的研究中没有考虑伴随陀螺特性的引入而实际存在的角动量装置的质量、惯量以及角动量装置与柔性体本身的耦合影响。Hu等[9]在D’Eleuterio的研究基础上，考虑了上述质量、惯量和结构耦合影响，基于多体动力学建模中常用的Kane方法，推导了带有可变速控制力矩陀螺(Variable-speed control moment gyro, VSCMG)柔性多体系统的通用动力学模型，为工程应用提供了较为完善的理论基础。但是，这一通用动力学模型带有较强的非线性，对于直接应用控制方法进行振动抑制难度较大。贾世元等[10]研究了约束陀螺柔性体结构的执行机构优化配置问题，基于最优控制理论，并应用遗传算法进行了配置优化求解，为主动振动控制中的执行机构部署提供了理论参考。然而，这种优化配置是最优控制意义上的，并没有对其他控制方法进行更深入的讨论。Hu等[11]对文献[9]中的约束陀螺柔性体系统动力学模型进行了线性化，以角速率陀螺为测量装置，推导了适用于控制器设计的状态空间模型，并使用自适应控制方法对其进行了控制器设计。然而，该方法直接应用降阶模型进行控制器设计，并没有考虑模态截断可能引起的控制器鲁棒性问题。

为了解决使用压电陶瓷元件作为执行器的发生控制溢出问题，Goh和Caughey[12]提出的正位置反馈(Positive postion feedback, PPF)控制方法能够在满足同位控制条件时有效解决控制溢出问题，同时能够为闭环系统提供足够的模态阻尼，因而成为使用压电陶瓷元件作为执行器时广泛应用的控制方法[13]。然而，虽然PPF控制器本质上是一种具有3个可调参数的二阶滤波器，结构简单，但是选择PPF参数的方法却不尽相同。Fanson[14]采用了根轨迹方法按照由高阶到低阶的顺序进行PPF参数选择。这一方法的不足是设计中需要反复迭代。Starek和Fenik[15]提出了一种解析法的PPF最优参数的设计方法，然而该方法只能应用于单输入单输出(SISO)系统。Friswell和Inman[16]提出了一种可同时用于SISO和MIMO系统中的PPF输出反馈最优参数设计方法，但是该方法所确定的参数依赖于系统的初始条件。Moheimani等[17]提出了一种基于极点配置和最小化闭环系统无穷范数两种优化准则的非线性搜索算法，然而这一算法依赖于LMI方法求解出的初值。Orszulik和Shan[18]使用遗传算法替代非线性搜索算法，对文献[17]的算法进行了改进。但是依旧存在计算多阶模态情况耗时长的问题。

综上所述，陀螺柔性体振动控制方法在鲁棒性设计方面和PPF控制器参数优化设计效率方面仍有提升空间。本文以带有VSCMG的柔性太阳翼为被控对象，提出了一种基于求解非光滑H∞综合问题的最优参数PPF主动振动抑制方法：在建立线性化约束陀螺柔性板动力学模型基础上，不同于以往文献将角速率陀螺作为测量装置的方案，选用角度陀螺作为测量装置，推导了约束陀螺柔性板全阶状态空间模型；为提高MIMO系统控制多阶模态情况下的最优PPF控制器参数的选取效率，给出了一种通过对被控对象全阶状态空间模型进行降阶、修正和加权处理，将对应的PPF控制器参数优化问题转化为在PPF控制器构型约束条件下的非光滑H∞综合问题并进行参数寻优的PPF最优参数确定方法。本文提出的最优参数PPF主动振动抑制方法能够实现对各阶陀螺模态的独立控制，在满足快速性和鲁棒性等控制需求的前提下，能够稳定高效地实现PPF最优参数的求解。数值仿真的时域和频域分析表明该方法能够快速、鲁棒地实现带有VSCMG的柔性太阳翼的振动抑制。

1 带有VSCMG的柔性太阳翼振动控制模型

1.1 带有VSCMG的柔性太阳翼建模和模态分析

典型的航天器本体及带有VSCMG的柔性太阳翼结构示意图如图1所示，主要包含航天器本体和与航天器本体刚性连接并带有VSCMG的柔性太阳翼。这种柔性太阳翼结构中安装有若干个用于抑制其结构振动的VSCMG。以带有n个VSCMG的柔性太阳翼作为研究对象，将刚性连接对应成固定端约束，可以得到如图2(a)所示的约束陀螺柔性板构型。

图1 带有VSCMG的柔性太阳翼航天器结构示意图Fig.1 Structure diagram of flexible solar panel spacecraft with VSCMG

图2 约束陀螺柔性板示意图Fig.2 Schematic diagram of constrained gyroelastic plate

包含有限个VSCMG的多体系统通用动力学方程已由文献[9]的式(7)得到。通过将该式中的速度及角速度置零，并忽略高阶项可得线性化的约束陀螺柔性体动力学方程为

(1)

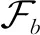
(2)

因而，对应于第1个初始安装方向的VSCMG能够产生沿xb负向的控制力矩；对应于第2个初始安装方向的VSCMG能产生沿yb负向的控制力矩。

根据式(2)，Ma,Ga和Bτ可以推导简化为

(3)

为进行约束陀螺柔性板的模态分析，将线性化方程写成一阶系统形式

(4)

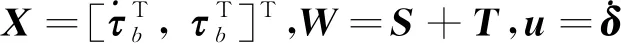
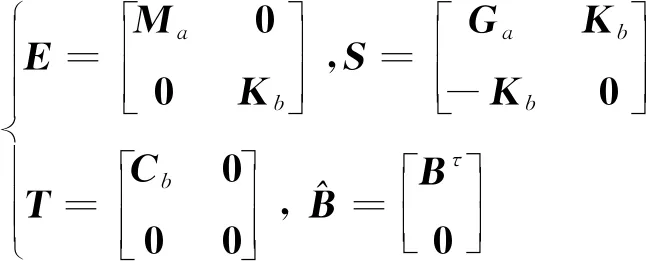
(5)

对于不考虑T的无阻尼约束陀螺柔性体系统，忽略右端的外界激励项进行模态分析，式(4)的特征值问题变为

λαEφα+Sφα=0

(6)

其中，λα为上述方程的特征值，φα为对应于特征值λα的特征向量。由于E矩阵的正定对称特性，以及S矩阵的反对称特性，可知λα=jωα，α=±1,…,±m，ωα=-ω-α，φα=fα+jkα并且f-α=kα。实数向量fα和kα具有以下形式[11]

(7)

式中：vα=μ-α且μα=v-α。

由上述特性可知，矢量对(μα,vα)在α=1,…,m时即可完整描述约束陀螺柔性体的模态特性，矢量对(μα,vα)即为约束陀螺柔性体的陀螺模态[11]。此外，实数向量fα和kα还满足正交条件[11]

(8)

式中：δαβ为Kronecker符号。

对于考虑T的有阻尼约束陀螺柔性体系统，将柔性阻尼T作为无阻尼约束陀螺柔性体系统的摄动部分进行考虑，则有阻尼约束陀螺柔性体系统的特征值为[11]

(9)

其中，δλα=ζαωα,ζα为阻尼摄动因子且满足

(10)

(11)

(12)

(13)

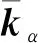
(14)

1.2 状态空间模型

将式(14)代入式(4)，并应用式(13)的正交化条件进行形式化简，可以得到约束陀螺柔性板的状态空间方程

(15)

(16)

考虑到本文后续控制器设计中所使用的正位置反馈PPF控制方法并充分发挥其在同位控制[19]条件下的优势，采用与VSCMG同位部署的角度陀螺作为测量装置，提供对应于力矩的“角位置”信息，进而使约束陀螺柔性体能够满足同位控制条件。与图2(a)对应的输出矩阵C的具体形式为

(17)

2 最优参数PPF控制器设计

2.1 PPF控制方法

PPF控制器的结构简单，具有很强的工程易实现性；特别是在传感器与执行器的部署满足同位控制条件下，PPF控制方法能够有效解决控制溢出问题[19]。这些优点使得它被广泛应用在柔性结构的振动控制中。

PPF控制方法的基本原理是基于广义的结构位置输出量测量生成用于抑制结构振动的广义力控制指令。这种广义位置输出量和对应的广义力控制量，既可以是平移位移量与对应的力，也可以是转动位移量与对应的力矩。PPF控制方法本质上是一种二阶补偿器，它将测量得到的结构位置信息输入二阶滤波器，再将二阶滤波器的输出信号保持正号的反馈给结构，是一种典型的正反馈控制。PPF控制结构图如下图所示。

图3 PPF控制结构图Fig.3 Structure diagram of PPF control

对于本文研究的约束陀螺柔性体板振动控制问题，应用PPF控制方法进行控制器设计所选取的广义位置输出量为柔性体角位移，对应的广义力控制量为VSCMG输出的陀螺力矩。

对于第i阶模态的PPF控制器而言，设计的主要内容是选取控制器结构中的三个设计参数：控制器增益Ki、控制器阻尼比ξci以及控制器结构频率ωci。这三个设计参数选取的优劣直接决定PPF控制器的控制性能。当期望控制的模态个数为q时，对应的PPF控制的设计参数个数将为3q。当执行器与测量装置满足同位控制条件时，对应的PPF控制器传递函数阵应为对角矩阵，对于带有n个VSCMG的约束陀螺柔性体板而言，第j个对角元素为第j个VSCMG将要控制的对应阶PPF控制器传递函数的线性组合，即

(18)

式中：lji即为第i阶模态被第j个VSCMG所控制的判断标志位。

PPF控制器参数选取的一般方法是基于古典控制中的根轨迹和频率设计理论反复迭代设计，或者采用试凑法进行手动调节。这些方法的设计效率不高同时对设计人员经验要求较高。本文将采用一种基于求解非光滑H∞综合问题的PPF控制器参数寻优方法，实现约束陀螺柔性板的最优PPF参数的高效求解。

2.2 基于非光滑H∞综合的参数优化

固定构型控制器非光滑H∞综合的基本原理是在满足预定控制器构型约束的稳定控制器集合中，对闭环系统无穷范数进行最小化。固定构型控制器H∞综合的非光滑特性主要来自于两个方面:一是H∞范数定义中的最大奇异值求解过程；二是在全频域内对最大奇异值进行最小化过程。对于本文所研究的约束陀螺柔性板控制问题而言，预定构型约束即为PPF控制器构型约束。

不失一般性，对于一个线性定常系统，标准状态空间表达式可以记为

(19)

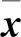
则固定构型控制器非光滑H∞综合问题可以描述为：

(20)

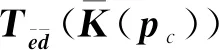
对于该非光滑H∞综合问题如果使用传统“最速下降法”进行寻优，会由于优化指标函数的非光滑特性，无法收敛。因而本文选用文献[20]中的“一阶下降算法”进行上述优化问题的求解。

2.3 H∞框架转化和控制模型处理

考虑到振动系统整体响应主要决定于其低阶模态，并且为使所设计的控制器具有合理的规模，需要对约束陀螺柔性板的全阶状态空间模型进行降阶处理。对于式(15)表示的约束陀螺柔性板的全阶状态模型，可将其分离为由前nr个模态组成的降阶系统模型Gmod以及由后m-nr个模态组成的剩余系统模型Gun-mod。

此外，为使PPF控制器参数优化设计过程能够在H∞框架下进行，需要对降阶模型进一步处理。

控制器设计的总体框架如图4(a)所示。控制目标是在指定的扰动量级和控制输入量极限值约束条件下，使评价输出量足够小。在H∞框架下，这一控制目标是通过在稳定控制器集合中，对从扰动输入量到评价输出量的闭环传递函数矩阵H∞范数进行最小化来实现的。然而，评价输出量可以由对应于不同控制目标的多个物理量(如控制输入量和性能指标量)共同组成，这将导致不同控制目标需要在同一个闭环传递函数矩阵H∞范数指标下表示，为此必须对图4(a)中总体框架的输入量和输出量进行加权处理。

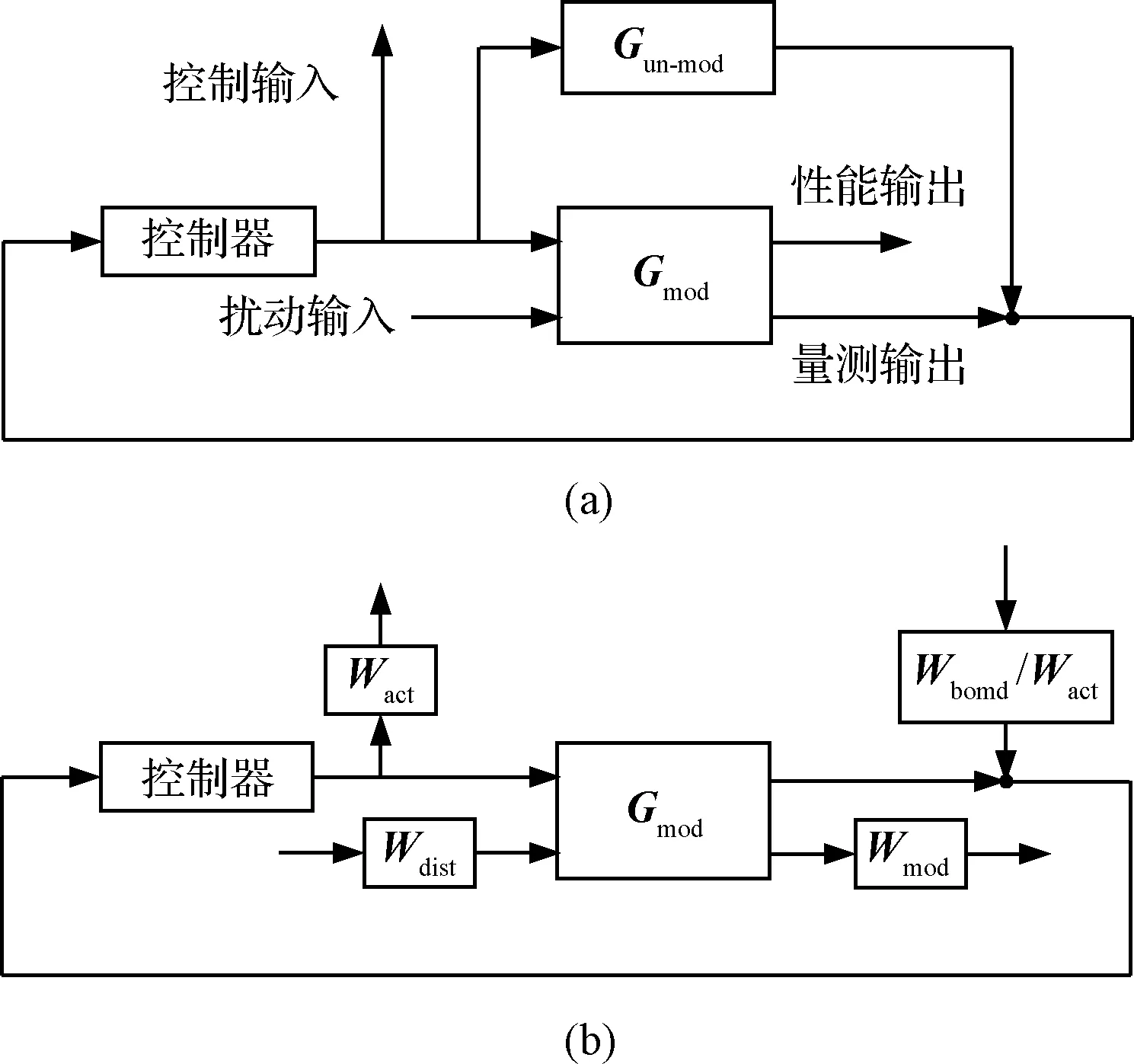
图4 总体框架和H∞框架示意图Fig.4 Overall framework and H∞ framework diagram

如图4(a)所示，式(15)表示的全阶系统模型可由模型Gmod和Gun-mod相加得到。其中Gmod代表降阶系统模型，包含那些主导系统响应的低阶模态；Gun-mod代表剩余系统模型，由降阶过程中忽略的高阶模态组成。

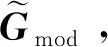
此外，模型降阶会引起控制溢出问题，即当通过降阶模型设计的控制器应用于全阶系统或者实际系统时，被忽略的高阶模态将引起附加控制量和观测量，进而导致闭环系统不稳定。在H∞框架里，控制溢出问题可以通过引入基于小增益定理[23]的鲁棒性指标来解决。

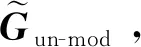
3 算例仿真与分析

本部分将结合一个仿真算例，应用本文提出的最优参数PPF控制方法对带有VSCMG的航天器柔性太阳翼进行主动振动抑制。

仿真算例中所使用的柔性太阳翼和VSCMG相关参数见表1。两个VSCMG分别安装在柔性板的两个非约束端外边缘角处，如图2所示。两个陀螺转子角动量方向zgi均垂直于柔性板，与zb方向相同；两个陀螺的框架转动方向xgi相互垂直，分别与xb和yb同方向。

表1 柔性板和VSCMG的参数Table 1 Parameters of flexible plate and CMGs

使用有限元软件ANSYS中的六自由度壳体结构单元“SHELL 181”对柔性板进行建模，保留前10阶模态作为柔性板的有限元输出模型用于后续的陀螺柔性体建模与分析。这10阶模态的固有频率分别为：0.03568454 Hz，0.12965534 Hz，0.2229134 Hz，0.4342954 Hz，0.6210046 Hz，0.7068573 Hz，0.87604482 Hz，1.013184 Hz，1.284289 Hz，1.515107 Hz。前四阶的柔性体模态如图5所示。

图5 前4阶柔性板模态图Fig.5 The first four modal diagram of the flexible plate

柔性板中加入VSCMG后，约束陀螺柔性体模态频率变为：0.03565845 Hz，0.1294373 Hz，0.2228697 Hz，0.4338221 Hz，0.6207935 Hz，0.7053909 Hz，0.8758507 Hz，1.011640 Hz，1.284282 Hz，1.514929 Hz。前四阶的柔性体模态如图6所示。

图6 前4阶陀螺模态图Fig.6 The first four gyroelastic modal diagram

由图6的仿真结果可知，第1阶与第3阶陀螺模态主要为yb方向弯曲变形，与第2个VSCMG产生的陀螺力矩方向相一致，因而在控制器设计时使用第2个VSCMG控制第1阶与第3阶陀螺模态。第2阶陀螺模态对应的变形主要发生在xb方向上，与第1个VSCMG产生的陀螺力矩方向接近，因而在控制器设计时使用第1个VSCMG控制第2阶陀螺模态。此外，使用文献[25]的方法进一步分析模态占比可知，本算例中的约束陀螺柔性体的变形主要由前3阶模态主导，为此，降阶系统模型Gmod包含前3阶模态，剩余系统模型Gun-mod包含后7阶模态。基于上述分析，由式(18)可以得到本算例PPF控制器KPPF(s)的结构形式为

(21)

图7 剩余系统性能界计算结果Fig.7 Performance boundary of the residual system

考虑到PPF方法进行主动振动抑制本质上是提高各阶模态阻尼，同时为使前3阶模态对于扰动输入的过渡过程时间尽可能相等，权值函数Wdist,Wact和Wmod的选取结果如表2所示。

表2 权值函数的选取结果Table 2 Selection result of weight functions

而后，为应用“一阶下降算法”对固定构型控制器非光滑H∞综合进行优化求解，需要对PPF参数的搜索范围进行合理限定：PPF控制器的结构频率ωci限定在对应阶次陀螺模态ωi固有频率的±30%以内[13]；控制器增益Ki限定为正数；控制器阻尼比ξc的范围限定在0～1范围内。

通过非光滑H∞综合方法进行参数寻优，得到的最优PPF控制器参数见表3。

为了验证所设计控制器的有效性，对全阶模型闭环系统进行频域和时域分析。在第一个VSCMG的位置施加一个zb方向的外部扰动激励，并以该点的zb方向振动位移值(以下记为端部响应)作为控制器性能的评价指标，图8给出了从外部扰动激励

到端部响应的频域响应曲线。

从图8可以看出，闭环系统的前三阶模态振型频率附近的响应幅值相对开环系统明显下降，其中一阶模态的响应幅值由18.56 dB下降至-21.81 dB，下降幅度为40.37 dB；二阶模态的响应幅值由2.52 dB下降至-12.54 dB，下降幅度为15.06 dB，三阶模态的响应幅值由-19.52 dB下降至-35.94 dB，下降幅度为16.42 dB。上述结果说明所设计的最优参数PPF控制器实现了对前三阶模态阻尼的有效提高，进而实现了振动控制的目的。

图8 频域响应曲线图Fig.8 Frequency response curve

时域分析的仿真条件为：外部扰动激励幅值为5 N，持续时间为一阶陀螺模态振动周期的一半，激励形式为脉冲激励。端部位移的时域响应曲线如图9所示，VSCMG框架角速度的时域变化曲线如图10所示，前4阶物理模态的时域响应曲线如图11所示。

从图9可以看出，在所设定的脉冲激励下，系统的振动过程由开环时的缓慢衰减(无明显衰减趋势)，过渡过程时间远大于500 s，变为闭环时的迅速衰减，过渡过程时间显著降低至150 s以内。闭环系统的端部振动的衰减速度相对于原系统显著提高，即最优参数PPF控制器使闭环系统的模态阻尼显著增加。由图10可知，VSCMG的框架角速度输出均在0.5 rad/s以内。从图11可以看出，从闭环系统各阶模态的响应时间接近，与PPF控制器设计过程中权值函数的设计初衷相一致。

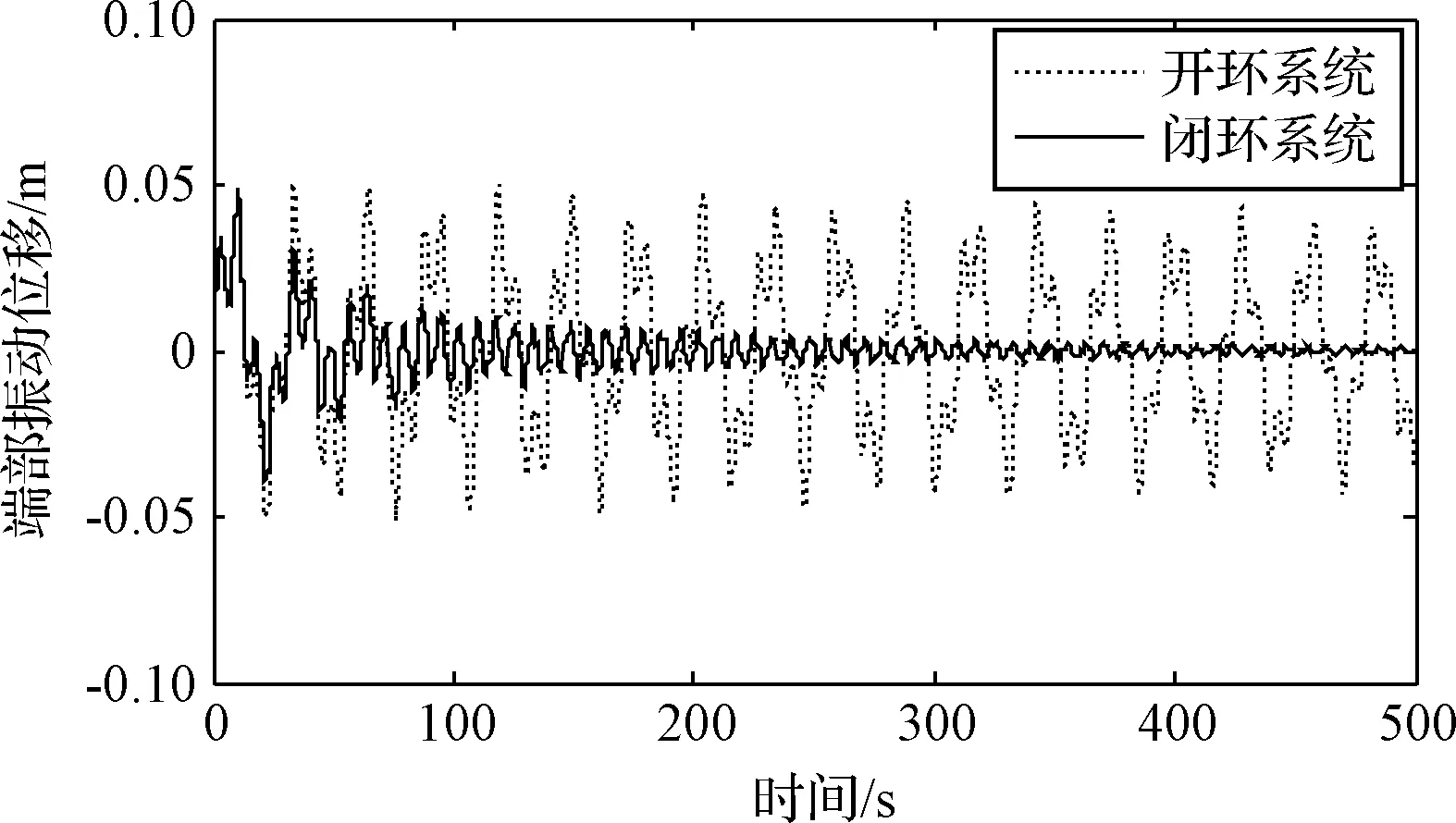
图9 端部位移的时域响应曲线Fig.9 Time domain response curve of tip displacement

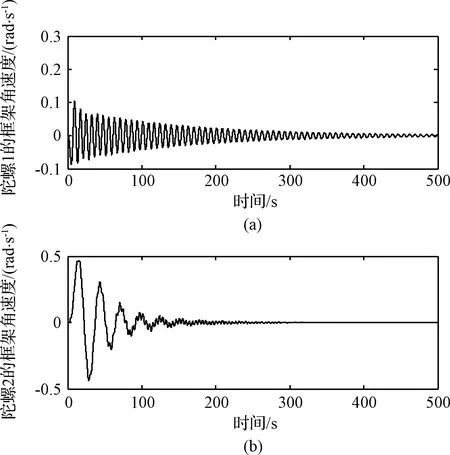
图10 陀螺框架角速度的时域变化曲线Fig.10 Time domain variation curve of gyro frame’s angular velocity

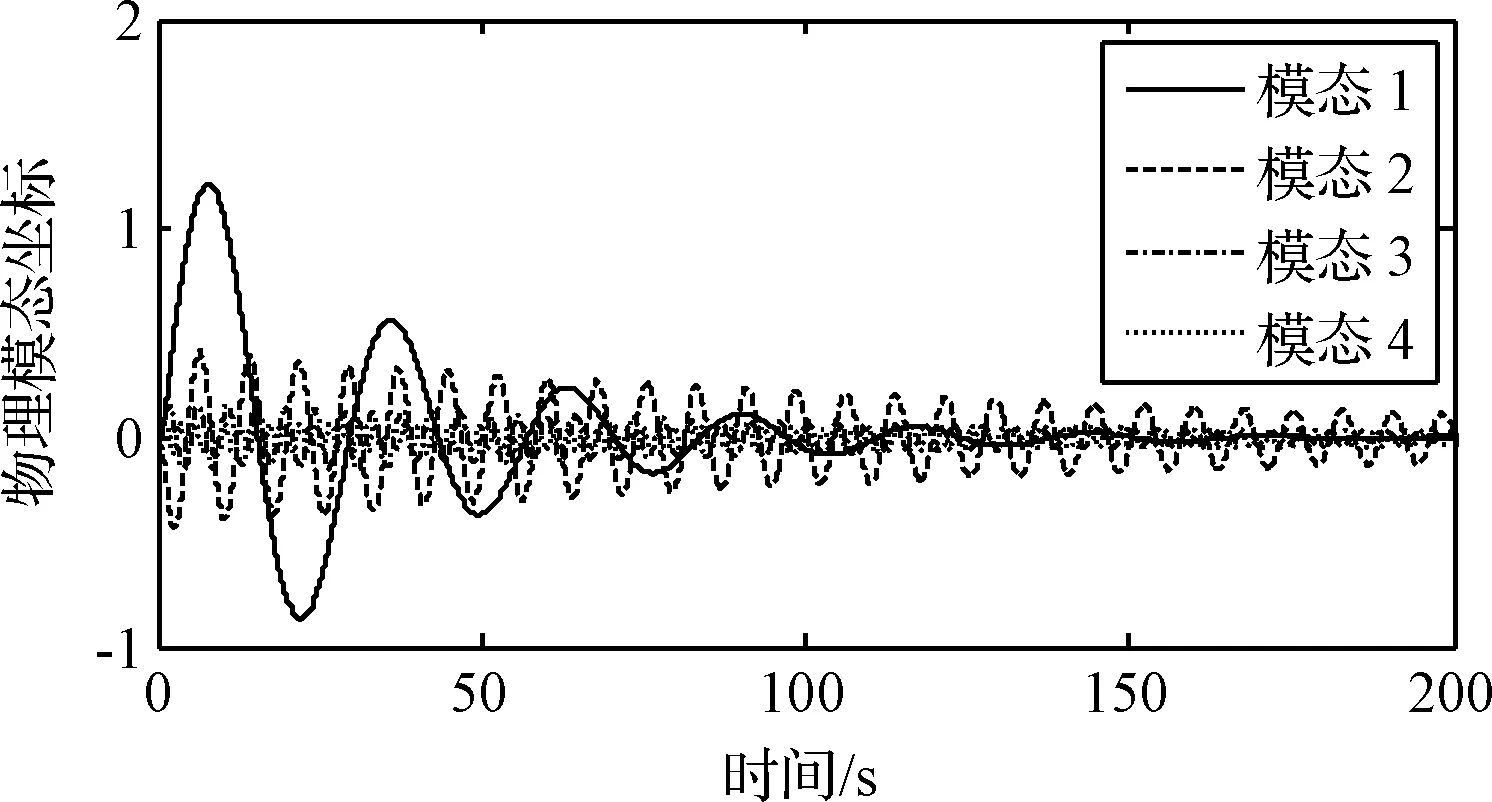
图11 前4阶物理模态的时域响应曲线Fig.11 Time domain response curve of the first four physical modes

以上频域分析和时域分析直观地说明了所设计的最优参数PPF控制器能够实现对各阶陀螺模态的独立控制，显著增加各阶模态的阻尼，实现快速、鲁棒的振动抑制。

4 结 论

本文研究了带有VSCMG为执行机构的柔性太阳翼振动抑制问题，提出了一种基于求解非光滑H∞综合问题的最优参数PPF控制方法。以角度陀螺为测量装置，应用PPF控制方法进行振动抑制，并将对应的PPF控制器参数优化问题转化为在PPF控制器构型约束条件下的非光滑H∞综合问题，使PPF控制器参数能够在H∞框架下进行高效寻优求解，有效提高了陀螺柔性体振动控制方法的鲁棒性以及PPF控制器参数优化设计的计算效率。仿真算例中的一阶、二阶和三阶模态的响应幅值分别下降了40.37 dB, 15.06 dB和16.42 dB，过渡过程时间显著降低至150 s以内。通过仿真结果可以看出，最优PPF控制方法能够有效解决带有VSCMG的柔性太阳翼振动问题，所设计的最优参数PPF控制器能够实现对各阶陀螺模态的独立控制，显著增加各阶模态的阻尼，实现快速、鲁棒的振动抑制。