COVID-19重大疫情下的电网负荷趋势评估新方法
谢家安,莫颖生,王玉荣
(1.广东电网有限责任公司佛山供电局,广东 佛山 528000;2. 东南大学 电气工程学院,江苏 南京 210000)
2019年12月,新型冠状病毒(世界卫生组织命名COVID-19)在中国武汉地区发生人际间快速传播,其高度传染性[1-2]与春节期间人员流动高密度性的叠加效应,导致疫情在全国范围内快速传播。为快速阻断疫情的发展,国家卫健委在2020年1月20日宣布中国大陆地区进入一级响应状态,开始在全国范围内对人员流动和生产经营活动采取严格的管理和限制措施。一系列措施不仅给我国经济和社会生产活动造成了巨大影响,也给电力系统的安全稳定运行带来了巨大挑战。
疫情严重期间,电力系统从业人员到岗率大幅降低,团队协作方式打乱,系统化应急能力严重不足,大量可能导致电网事故的临界缺陷问题无法及时解决;同时,电网负荷大幅降低,致使大量发电设备低负载运行甚至退出电网运行,容易引起系统频率异常波动、运行过电压、无功补偿不足等问题,且严重降低电网运行的经济性,从而影响电网运行的安全性、稳定性。因此,对本次COVID-19疫情给电力系统正常运行所造成的实际影响进行快速、有效的指标化评估,是一项非常紧迫和重要的工作,具有重要意义。
电力系统负荷曲线是表征电力系统电量平衡、分析运行方式、确定潮流分布和电源优化以及可靠性计算的基础资料,学者们针对其应用进行了大量研究,在用电模式识别[3-6]、负荷预测[7-11]、负荷参数识别及电网可靠性分析[12-15]、电网负荷与国民经济相关性[16-17]等方面取得了较多的研究成果。
文献[4]提出一种基于双层聚类分析的负荷形态组合识别方法,是以传统的欧式距离(Euclidean distance,ED)作为曲线相似度的判据,对曲线进行聚类分析;但以传统的欧式距离相似性判据的方法难以区分距离相近而形态差异明显的负荷曲线,不能有效识别曲线形态进而导致聚类分析失效,使用局限性较大。文献[6]提出一种自适应分段近似的曲线形态聚类算法,通过对负荷数据进行可变时间分析率重构,并对重构数据使用形态聚类k-shape算法进行相似性计算,实现对典型负荷曲线的形态聚类分析;但该方法只考虑了负荷曲线的形态相似度,而忽略了负荷曲线在时间尺度上动态幅值差异的重要信息,可能导致聚类分析失效。因此,单纯以欧式距离或形态聚类k-shape计算结果作为判据,均无法满足准确描述电力系统实际负荷曲线相似性的要求,无法实现对负荷曲线趋势的准确评估。
基于此,本文提出一种基于二分段-D-shape的负荷趋势评估新方法:首先以相邻正常年份春节假期后的电网负荷曲线进行样本训练,依据相似度指标训练出1条标准日负荷曲线;再利用二分段-D-shape评估法对本年度COVID-19疫情下的负荷曲线进行相似度指标计算,实现对COVID-19疫情下负荷曲线趋势特性快速、有效的指标化评估;最后通过多个实例分析验证本文提出方法的可行性、有效性和实用性。
1 时间序列相似性理论
1.1 欧氏距离度量法
在时间序列的相似度计算领域,常采用欧式距离法进行计算分析[18],通过计算时间序列的欧式距离,实现其相似度的量化分析。
欧式距离定义:n维时间序列分别为X=x1,x2,…,xn和Y=y1,y2,…,yn,则X、Y之间的欧式距离
(1)
利用欧氏距离对时间序列的稳态距离差异的高度灵敏性,可对n维时间序列X、Y进行相似度比较,其欧氏距离值在[0, +∞]之间。该值越小相似度越大,值越大则相似度越小,当值为0时,时间序列完全相似。
同时,欧氏距离对时间序列的噪声和突变点异常敏感,因此在度量随机时间序列相似度时,缺乏足够精度,其使用范围受到了一定限制。
1.2 余弦相似度度量法
余弦相似度度量法是通过计算相同维度时间序列的夹角余弦值,度量它们之间的相似性[19-23],实现其相似度的量化分析。
余弦相似度定义:n维时间序列分别为X=x1,x2,…,xn和Y=y1,y2,…,yn,则X、Y之间的余弦相似度
(2)
余弦相似度值在[-1,1]范围内,值越趋近于1时,2个时间序列正向相似度越高;越趋近于-1时,则反向相似度越高;趋向于0时,表示2个时间序列趋近正交。
由于余弦相似度度量法在计算n维时间序列X、Y的相似度时,只计算时间序列的夹角余弦值,与时间序列的向量幅值无关,无法有效反映出时间序列的幅值差异化,在实际应用中会受到一定条件限制。
2 负荷趋势二分段-D-Shape评估法
在实际电力系统中,某一个时间段内的日负荷曲线不仅在曲线形态上具有一定的相似性,在幅值上也会有较大的差异性;因此,不能单纯地从负荷曲线的幅值差异化或形态相似性来评估该区间段内的日负荷曲线趋势。
为此,本文提出一种基于二分段-D-Shape的区间段负荷趋势评估新方法,对本年度春节假期结束后一个时间段内的日负荷曲线进行相似度指标计算,可实现对节后负荷曲线趋势特性的有效分析。
2.1 标准日负荷曲线训练
以相邻正常年份春节假期后的第1天作为样本提取的起点,取连续5 d的日负荷曲线作为第1个训练样本矩阵,记为T=[T1T2T3T4T5]T,则任意样本矩阵T=[TmTm+1Tm+2Tm+3Tm+4]T,m为自然数,其中Tm,…,Tm+4均为n维日负荷数据序列。样本矩阵T的相似度指标
(3)
其中
(4)

设γ为相似度指标阈值,本文中γ=0.95。当ρ(Ti,Tj)≥γ时,可以确定m的取值,进而确定标准日负荷曲线为
(5)
式中μ为修正系数,它由相邻年份的经济增长率R、电力负荷与GDP的Pearson相关系数r共同决定[16-17],
μ=r(1+R).
(6)
通过前述方法可训练出标准日负荷曲线X,为基于二分段-D-Shape的春节假期后负荷趋势的评估法奠定了良好基础。
2.2 二分段-D-Shape评估法

(7)
(8)
(9)
式中:系数α1、α2分别为分段时间序列1和分段时间序列2的权重;k1、k2分别为分段时间序列1的峰值比例系数和分段时间序列2峰值比例系数。
由式(7)可知,相似度指标ρ(X,Y)的取值范围在[0,1]之间。当ρ(X,Y)越小,被分析日负荷曲线与标准日负荷曲线相似性越低;ρ(X,Y)越大,被分析日负荷曲线与标准日负荷曲线相似性越高;当ρ(X,Y)=1时,被分析日负荷曲线与标准日负荷曲线完全一致。
2.3 日负荷曲线的状态划分
计算COVID-19疫情下,春节假期后1个时间段内的日负荷曲线与标准日负荷曲线之间的相似度指标ρ(X,Y)的值,在此基础上,通过式(10)实现对日负荷曲线的状态划分:

(10)
式中λ是常数,本文依据实际工程应用要求,设置λ=0.98。
由上述分析可知,本文提出的基于二分段-D-shape法可实现对COVID-19疫情下日负荷曲线趋势特性的定量和定性分析,为COVID-19重大疫情下电网的稳定运行和相关决策提供可靠的理论依据。
2.4 负荷曲线趋势评估计算步骤
a)首先以相邻的正常年份春节后的电网日负荷曲线进行样本训练,依据相似度指标阈值γ为判据,训练出1条标准日负荷曲线。
b)利用二分段-D-Shape方法计算被分析日负荷曲线与标准日负荷曲线之间的相似度指标ρ(X,Y)。
c)基于ρ(X,Y),实现对日负荷曲线趋势特性的定量和定性分析。
3 实例分析
3.1 实例1
2018年农历春节假期结束后,广东电网有限责任公司(以下简称“广东电网”)佛山供电局监测到连续20 d的全网日负荷曲线,以及根据2017年春节后样本训练出的标准日负荷曲线分别如图1和图2所示,图中P为日负荷曲线的有名值,t为时间。

图1 2018年2月22日至3月13日的日负荷曲线Fig.1 Daily load curves from February 22 toMarch 13, 2018

图2 训练的标准日负荷曲线(实例1)Fig.2 Trained standard daily load curve in example 1
归一化的日负荷和标准负荷曲线分段序列1、日负荷和标准负荷曲线分段序列2分别如图3(a)、(b)和图4(a)(b)所示,图中P*表示日负荷曲线的标幺值。

图4 日负荷和标准负荷曲线分段序列2(实例1)Fig.4 Second segment of daily load and standardload curves in example 1

图3 日负荷和标准负荷曲线分段序列1(实例1)Fig.3 First segment of daily load and standard load curves in example 1
应用本文提出的二分段-D-shape评估方法,对2018年春节假期结束后恢复期的电网负荷趋势进行评估,评估结果如图5所示。
由图5可知:2018年春节假期结束后,电网负荷经过一个快速恢复期,在节后第12天(即2018年3月5日)时,日负荷曲线的相似度指标ρ(X,Y)=0.99,表明电网负荷的恢复期结束,已经进入稳定区,说明此时社会生产和经济活动均已恢复到正常状态,本地区的国民经济运行进入稳定运行状态。
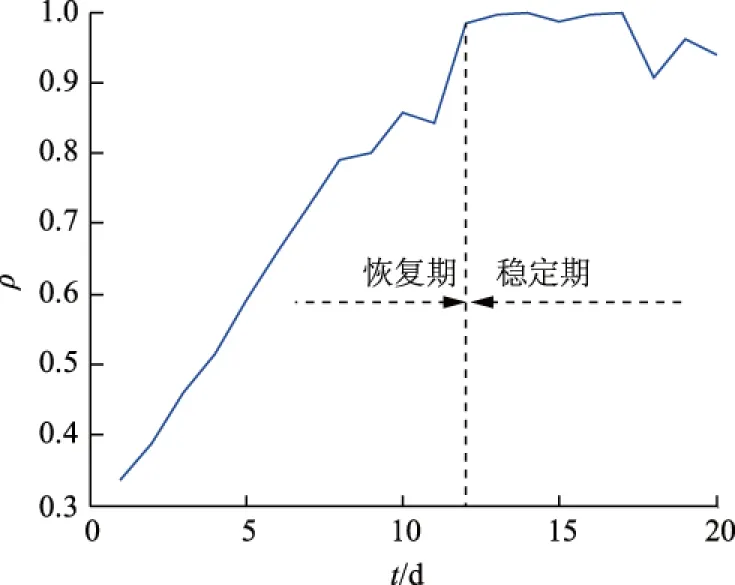
图5 日负荷曲线趋势评估结果(实例1)Fig.5 Results of daily load curve trend assessment of example 1
3.2 实例2
2019年春节假期结束后,广东电网佛山供电局监测到连续20 d的全网日负荷曲线,以及根据2018年春节后样本训练出的标准日负荷曲线分别如图6和图7所示。

图7 训练的标准日负荷曲线(实例2)Fig.7 Trained standard daily load curve in example 2

图6 2019年2月11日至3月2日的日负荷曲线Fig.6 Daily load curves from February 11 to March 2, 2019
归一化的日负荷和标准负荷曲线分段序列1、日负荷和标准负荷曲线分段序列2分别如图8(a)、(b)和图9(a)、(b)所示。

图9 日负荷和标准负荷曲线分段序列2(实例2)Fig.9 Second segment of daily load and standard load curves in example 2

图8 日负荷和标准负荷曲线分段序列1(实例2)Fig.8 First segment of daily load and standard load curves in example 2
应用本文提出的二分段-D-shape评估方法,对2019年春节假期结束后恢复期的电网负荷趋势进行评估,结果如图10所示。

图10 日负荷曲线趋势评估结果(实例2)Fig.10 Results of daily load curve trend assessment of example 2
由图10可知:2019年春节假期结束后,电网负荷经过15 d的快速恢复期后(即2019年2月25日),日负荷曲线的相似度指标ρ(X,Y)=0.989,表明电网负荷已经进入稳定区,已经恢复到正常水平,即本地区的社会生产和经济活动已经恢复到正常运行轨道。
3.3 实例3
2020年春节假期结束后,COVID-19疫情给我国的社会生产和经济活动造成了重大影响,通过对电网负荷曲线趋势进行评估,可有效评估疫情对我国经济和社会生产的影响程度,为疫情下的电网决策提供依据。
广东电网佛山供电局监测到的2020年春节假期结束后连续54 d的全网日负荷曲线如图11所示。
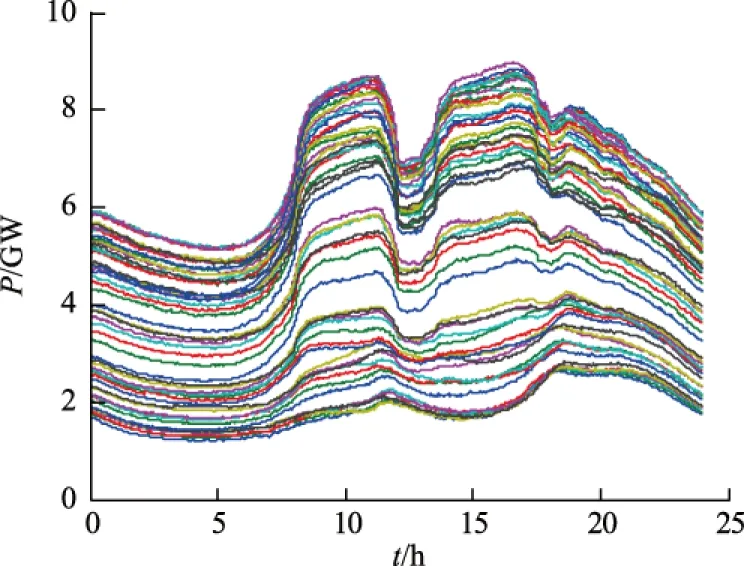
图11 2020年2月3日至3月19日的日负荷曲线Fig.11 Daily load curves from February 3 to March 19, 2020
应用本文提出的二分段-D-Shape法对负荷曲线趋势进行评估,评估结果如图12所示。
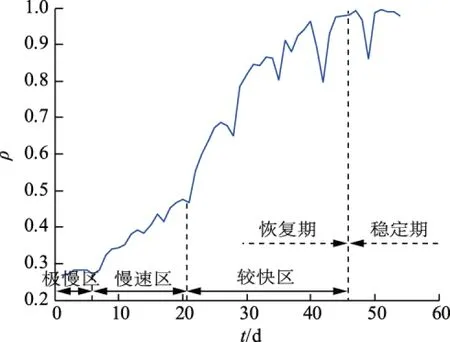
图12 日负荷曲线趋势评估结果(实例3)Fig.12 Results of daily load curve trend assessment of example 3
由图12可知,受COVID-19疫情的影响,2020年春节假期结束后,电网负荷经过了3个不同阶段恢复期。
第1阶段共6 d(2月3日至2月8日)的超低速恢复期,负荷相似度指标ρ(X,Y)<0.3,说明这个期间用电负荷基本保持在一个较低水平,社会综合复工率非常低。
第2阶段共16 d(2月9日至2月24日)的低速恢复期,负荷相似度指标ρ(X,Y)增长到0.49左右,说明这期间用电负荷基本保持一个较慢速度的增长,社会综合复工率达到了49%左右,仍处于很低水平。
第3阶段共24 d(2月25日至3月19日)的较快速恢复期。广东省卫健委在2月24日将全省防控级别由一级调整为二级之后,佛山地区的电网负荷经过24 d的较快速恢复期后,负荷相似度指标ρ(X,Y)增长到0.988,即负荷恢复期结束进入了稳定区,全社会工作日期间的综合复工率达到98%以上,表明佛山地区社会生产和经济活动已经基本恢复到正常状态,本地区国民经济运行基本进入了稳定运行状态。
4 结束语
本文提出一种基于二分段-D-shape的负荷趋势评估新方法,首先以相邻正常年份春节假期后的电网负荷曲线进行样本训练,依据相似度指标训练出标准日负荷曲线;再利用二分段-D-shape评估法对本年度COVID-19疫情下春节后的负荷曲线进行计算,可实现对节后负荷曲线趋势特性快速、有效的指标化评估,实例分析证明了本文方法的可行性、有效性和通用性,具有良好的实用价值。
后续将进一步深入研究电网负荷进入稳定区后,任意时间点发生重大灾害时,标准日负荷曲线的提取方法,以提高本文二分段-D-shape评估方法的适用范围。

