消费者均衡和生产者均衡的“镜像”分析
崔俊富,苗建军
(南京航空航天大学 经济与管理学院,江苏 南京 210016)
消费者和生产者是市场的参与者,消费者购买商品、服务,生产者提供商品、服务。消费者要实现固定预算的效用最大化或者固定效用的预算最小化,生产者要实现固定成本的产量最大化或者固定产量的成本最小化。[1]为了简化分析,本文仅讨论消费者实现固定预算的效用最大化和生产者实现固定成本的产量最大化。作为市场有联系的“对立”方或者“对面”方,消费者与生产者之间如同某个个体照镜子一样,可以与镜子中自己的“像”做出相同的动作、表情等等,消费者是生产者的“镜像”,生产者是消费者的“镜像”,他们追求利益最大化的行为具有相似性,因而对两者均衡的分析也具有相似性,某种程度上是“镜像”分析。[2]
一、消费者均衡
消费者购买商品是为了获得效用,不同的商品提供不同的效用,单个消费者如何选择不同商品以实现固定效用最大化便是消费者均衡的实现问题。消费者均衡可以使用三种方法来模拟,分别是逻辑分析法、几何分析法和数理分析法。逻辑分析法使用逻辑推理来模拟消费者均衡的实现,几何分析法使用几何推导来模拟消费者均衡的实现,数理分析法使用数理演算来模拟消费者均衡的实现。[3]
(1) 逻辑分析法

x1,x2,...,xn分别代表种 商品, p1,p2,...,pn分别代表种商品的价格。令分别代表种 商品带来的边际效用为货币的边际效用。如果

那么,消费者会选择增加单位价格边际效用较高的商品,减少单位价格边际效用较低的商品,最终会实现

该均衡条件意味着单位价格的不同商品带给消费者的边际效用应相等,等于一元钱的边际效用。逻辑分析法简单明了,通过简单的概念推理即可模拟消费者均衡的实现。[4]
(2) 几何分析法
几何图形是科学研究的有力工具,消费者均衡的模拟也可以借用几何图形来实现。以两种商品为例, M N 为消费者预算线, U1,U2,U3为无差异曲线。消费者不会选择无差异曲线上的点,因为无差异曲线 U2,U3代表的效用高于。消费者也不会选择无差异曲线上面的点,因为在的预算下,无法达到该效用水平。最终,消费者最优化的选择是选择E点,如图1所示。该点为消费者预算线与无差异曲线的切点,该点为的预算下所能达到的最大效用水平。[5]

图1 消费者均衡

斜率为

无差异曲线 U (x1,x2)符合

可得其斜率为

可得

该式即为式(3)。几何分析法最大的优点是直观,消费者均衡点的选择一目了然,就是E点,其最优值的计算转换为斜率等式。其缺点是几何图形严重受到空间维数的影响,1维空间、2维空间、3维空间都可以由几何图形来表示,但是空间维数一旦大于3维,就很难由图形来表示了,其斜率等式将转换为超平面的斜率等式,这与数理分析法的思想就类似了。
(3) 数理分析法
在数理上消费者均衡可以转化为约束最优化问题,也就是在固定约束下的效用最优化问题,约束最优化比较常见的方法是拉格朗日乘数法。约束方程是式(1),构建拉格朗日函数[6]

最优化的条件为

经过变换可得

该式即为式(3)。与逻辑分析法和几何分析法相比,拉格朗日乘数法具有明显的优点。一是通过最优解的求解,非常严谨地模拟了最优化的形成过程,导出式(11)。二是不再受到空间维数的限制,可以推广到多维空间的最优化模拟。[7]
二、生产者均衡
生产者是消费者的“镜像”,其行为与消费者是相似的,生产者如何选择不同的生产要素以实现固定成本的产量最大化便是生产者均衡的实现问题。生产者均衡同样可以使用逻辑分析法、几何分析法和数理分析法三种方法来模拟。
(1) 逻辑分析法

令mp1,mp2,...,mpn分别代表种 生产要素带来的边际产量,为货币的边际产量。如果

那么,生产者会选择增加单位价格边际产量较高的生产要素,减少单位价格边际产量较低的生产要素,最终会达到均衡条件

该均衡条件意味着单位价格的不同生产要素带给生产者的边际产量应相等,等于一元钱的边际产量。[8]
(2) 几何分析法
生产者均衡的模拟也使用几何分析法来实现。以两种生产要素为例。为生产者成本线,Q1,Q2,Q3为等产量曲线。消费者不会选择等产量曲线上的点,因为等产量曲线代表的产量高于。消费者也不会选择等产量曲线上面的点,因为在的成本下,无法达到该产量水平。最终,生产者最优化的选择是选择点,(见图2)该点为生产者成本预算线与等产量曲线的切点,该点为的预算下所能达到的最大产量水平。[9]
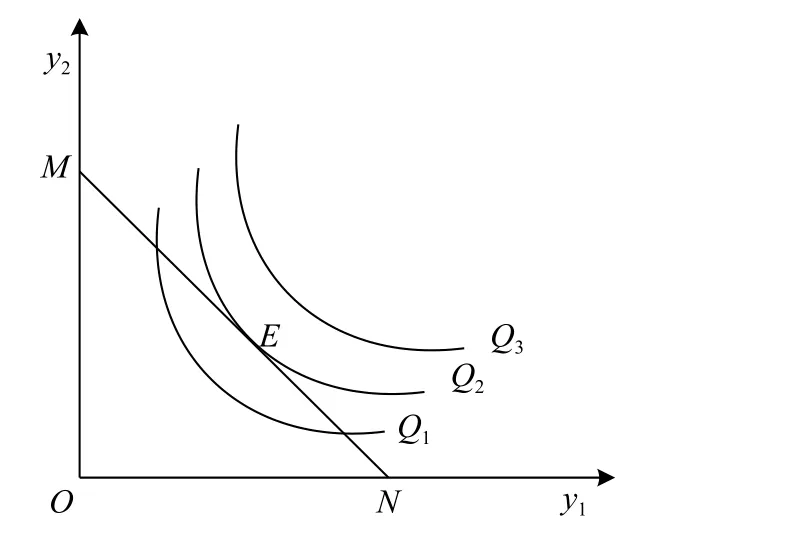
图2 生产者均衡

斜率为


可得其斜率为

可得

该式即为式(14)。与消费者均衡的分析类似,几何分析法最大的优点是直观,生产者均衡点的选择一目了然,就是E点,其最优值的计算转换为斜率等式。其缺点也是严重受到空间维数的影响,空间维数一旦大于3维,就很难由图形来表示了。[10]
(3) 数理分析法
在数理上生产者均衡可以转化为约束最优化问题,也就是在固定成本约束下的产量最优化问题。构建拉格朗日函数[11]
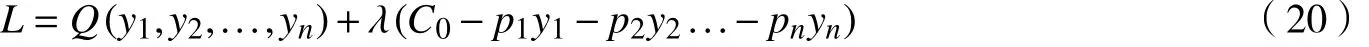
最优化的条件为

经过变换可得

该式即为式(14)。与消费者均衡的分析类似,数理分析法的优势可以非常严谨地模拟最优化的形成过程,导出式(22)。另外,不再受到空间维数的限制,可以推广到多维空间的最优化模拟。
三、生产者的自身“镜像”—生产与成本分析
上面分析了消费者均衡和生产者均衡存在“镜像”关系,其分析思路和分析方法是一致的。对于生产者自身,生产者的生产选择活动就是成本选择活动。因此,生产选择与成本选择也互为“镜像”,只是与消费者和生产者的“对立面镜像”不同,这种“镜像”关系更像是一面镜子的正面与背面。
(1) 生产函数与成本函数的“镜像”关系
生产函数改写为

成本函数改写为

这里存在一个不确定性,同一成本对应的生产要素组合 y1,y2,...,yn不一定是唯一的,因而同一成本值有可能对应了多个产量值。[12]如果施加非常严苛的条件,假定生产要素 y1,y2,...,yn为等比例的;或者多生产要素中仅有一种生产要素改变,而其他生产要素不变;或者是单生产要素函数,那么产量值和成本值就存在一一对应的关系,生产函数可转换为


(2) 短期对于劳动要素的讨论
经济学微观领域比较接近的情况是短期对于劳动要素投入的讨论,可以假定其他要素(土地、厂房、机器)是不变的。生产函数为

成本函数为

假定价格不变,因为其他生产要素都是常数,因而可以进行合并

其中, W =p1y¯1+p2y¯2...+pny¯n。
此时生产函数和消费函数将具有一些非常优良的性质。边际成本函数


根据边际成本函数和边际产量函数的关系以及平均成本函数和平均产量函数的关系,总产量函数为“S”型曲线,而总成本曲线为反“S”型曲线,如图3中和所示。在特别严苛的条件下,例如 yi=0,i≠L 且,总产量函数曲线和总成本函数曲线关于45°线对称,如图3中和所示。[13]

图3 生产曲线与成本曲线
四、结语
通过上面的分析可知,消费者和生产者作为市场的参与者,其行为具有相似性,消费者是生产者的“镜像”,生产者是消费者的“镜像”,都可以使用逻辑分析法、几何分析法、数理分析法对最优化进行模拟。生产者自身的生产分析和成本分析也是“镜像”分析,在特定的条件下,生产函数和成本函数可以转换为函数与反函数关系,例如短期对于劳动要素投入的讨论具有许多非常优良的性质。这种消费者和生产者“镜像”分析讨论也可以推广到经济学的其他领域。[14]

