带预载的弹簧柔性体在减振支柱设计中的应用
卢蕾蕾

摘 要:本文根据麦弗逊式悬架减振支柱的结构,在动力学仿真软件ADAMS中创建麦弗逊式前悬架动力学模型后,进行仿真用以分析弹簧对减振支柱的侧向力补偿。使用一种带预载的柔性体来模拟预压缩的悬架弹簧,通过与ADAMS自带的力向量弹簧模型进行对比,可知前者能够更准确地模拟“C”形弹簧的受力轴线随轮跳变化的情况。
关键词:预载;弹簧;柔性体
1 前言
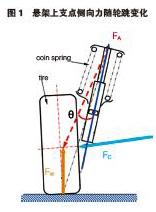
麦弗逊式前悬架具有结构简单,占用空间小的特点,因此在发动机前置前驱轿车上得到广泛的应用。其中的减振支柱总成除了具有缓冲、限位和减振的作用外,还在悬架机构运动中承担着导向和支撑的作用[1],使得减振支柱总成的设计尤为重要。要求减振支柱所受的侧向力尽可能的小,以减少活塞杆与减震套筒间的摩擦,提高零件的使用寿命。因此在设计其弹簧减振器总成时,通常会将弹簧受力轴线相对减振器轴线有一个向外的偏置角,以抵消支柱受到的侧向力,如图1所示。当弹簧力FA,控制臂球头力FC,地面反作用力FW交于一点时,减振器上支撑点所受侧向力为零。受到空间限制,弹簧下点无法向外偏移过大,同时悬架运动学的限制,弹簧下安装点相对于减振器上支撑点的运动轨迹为空间弧线,也就是说弹簧并非是沿着直线压缩和伸长,因此弹簧轴线的设计需要考虑车轮跳动时的受力情形。
2 力向量弹簧
在弹簧减震支柱的设计初期可在ADAMS软件中仿真其在工作中的受力状态。弹簧在ADAMS中被简化成一个因变形而产生力的弹性元件,通过一个连接弹簧上下硬点的力向量表达,力向量的大小则通过公式(1)计算得到[2]:
其中,Fs为弹簧力,K为弹簧刚度,D(i,j)为弹簧上下硬点之间的距离,随着车轮跳动而变化,ls为弹簧原长。通常情况下由于车身自身的重量作用,弹簧具有一定的预压缩量,其产生向上的支撑力Fs支撑车身,向下的压力Fs保持车轮在地面上滚动,故D(i,j)的初始长度小于ls。
在设计弹簧减振支柱总成时,需要分析减振器上支撑点的受力状况。如果弹簧设计合理,将会抵消大部分的侧向力,此时减振支柱上支撑点所受侧向力减小,只在轴向承受大部分载荷,故具有良好的耐久寿命。麦弗逊悬架中减振器的上支撑是由金属支架,轴承(提供车轮转向时所需的旋转自由度)和橡胶(起到过滤小幅振动的作用)等组成。仿真时用衬套的六个方向的刚度来表示,通过在后处理结果中查看衬套承受侧向力的大小可以确定弹簧力是否对侧向力有足够的补偿。
对麦弗逊悬架进行平行轮跳仿真,考察减振器上支撑衬套所受侧向力随轮跳变化。通过设计弹簧的偏置角,在轮跳为零时可以使上支撑点所受侧向力为零。但此时弹簧力向量较大,不满足弹簧布置所需空间的要求。同时,随着车轮上跳上支撑点所受的侧向力也逐渐增大,弹簧的侧向力补偿并未达到最优。因此在设计弹簧时,为了尽可能多地补偿侧向力,一般会采用弹簧轴线呈“C”形的“C”形弹簧以获得变化的弹簧偏移角,同时避免使弹簧下安装盘向外偏移过多,以节省侧向空间。
3 柔性体弹簧
设计中采用“C”形弹簧具有较好的效果,却无法在ADAMS中直接使用其自带的弹簧力向量去模拟“C”形弹簧,ADAMS软件算法将弹簧定义为一个力向量,方向沿“C”形弹簧上点的切线方向,却不能表示沿着“C”形弹簧轴线的力。为了更好地模拟沿弹簧力轴线变化的弹簧力,根据弹簧的实际形状,创建弹簧的柔性体模型代替力向量。
多体动力学软件一般采用模态综合法生成柔性体的模态中性文件,在计算时通过一个包含柔性体模态信息的矩阵文件描述柔性体,利用模态振型的线性叠加来表示柔性体的变形。对于施加了预载荷的柔性体模型,其矩阵文件还包含预载荷矩阵,通过一组数列描述分解在各个模态振型上的预载。在ADAMS中,柔性体的运动方程见公式(2):
其中,,,为柔性体广义坐标及时间导数;M为柔性体质量矩阵;为柔性体质量矩阵的时间导数;为柔性体质量矩阵对广义坐标的偏导数,是一个(N+6)×(N+6)×(N+6)的张量,其中N是模态阶数;K为广义刚度矩阵;fg为广义重力;D为模态阻尼矩阵;为代数约束方程;λ为约束方程的拉格朗日乘子;Q为施加的广义力[3]。
前文提到弹簧安装在悬架上时存在预压缩量,因此在生成弹簧柔性体时分两步:第一步,先对自由状态下的弹簧数模进行有限元前处理后进行固定边界的模态分析,生成模态中性文件;第二步,編制预载文件,重新计算生成带预载的模态中性文件。弹簧柔性体所受的预载必须为一对大小相等,方向相反的内力,将其从自由长度压缩至安装长度。此弹簧柔性体在导入ADAMS后,若在无约束状态下会从安装长度自动回弹至自由长度,在约束状态下则会对约束物体产生反作用力,这与公式(1)描述的力向量模型一致,也与弹簧在实际装配时的状态吻合。
4 结果对比
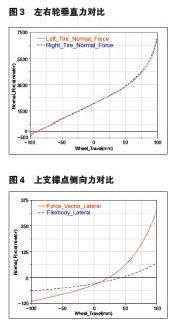
为便于对比,对一款上市车型的麦弗逊式前悬架创建动力学模型,右侧悬架使用带预载的柔性体弹簧,左侧悬架使用软件自带的单个力向量表示弹簧,创建模型如图2所示。为了使独立悬架的左右两侧互不影响,对悬架进行平行轮跳仿真,对比左右两侧悬架的轮胎垂向力以及减振器上支撑点的侧向力。由图3可以看出,左右两侧悬架所受的垂向力随轮跳的变化曲线基本相同,左右两侧悬架在设计位置(轮胎上跳量为零时)所受地面的反作用力均为2060N,说明柔性体弹簧的预压缩量产生的反作用力与实际一致,验证了柔性体弹簧模型的准确性。又可以从图4中看出,右侧悬架在车轮跳动时,其减震支柱上支撑点承受的侧向力要小于左侧承受的侧向力,且力随轮跳的变化曲线更平缓。说明弹簧与减振器夹角的设计可以有效的抵消侧向力,使得减振器上支撑点受到的侧向力小于设计要求的70N,避免减振器受到侧向力后产生磨损。可见,采用柔性体的弹簧模型有效地模拟“C”形弹簧的受力轴线,符合弹簧受力随着轮跳而变化的设计要求,从而验证了产品设计的合理性。
5 结论
在对产品进行仿真验证时,分析各个零件的设计意图是创建模型的关键,以此为前提采用合适的方法建模才能保证模型正确地模拟产品功能。麦弗逊悬架的减振支柱的受力分析关系到整个支柱总成的使用性能和寿命。在计算减振支柱的侧向力时,应考虑到弹簧受力的方向是随着车轮跳动位置而变化的。本文根据模态综合法创建弹簧柔性体,并施加预载后导入ADAMS软件进行建模仿真,模拟弹簧在悬架跳动时的变形过程。通过与ADAMS自带的弹簧模型对比,验证了模型的可行性和准确性。这种方法在带有预载荷的模型中都可以使用,为动力学建模提供了一种新的思路,拓宽了刚柔耦合模型在实际工程中的应用范围。
参考文献:
[1]姜鹏,汽车悬架系统的仿真分析与参数优化设计[D].浙江大学,浙江:2006.8-9.
[2]Using ADAMS/Car.2013.
[3]Using ADAMS/Flex.2013.From The Automotive Chassis: Engineering Principles,J. Reimpell & H. Stoll, SAE 1996.

