城镇污水处理厂进水水质变化规律研究
张 琨, 孙国胜, 赵 焱
(1.广东粤港供水有限公司,广东 深圳 518000;2.广东粤海水务股份有限公司,广东 深圳 518000)
城镇污水处理工艺应保持在最佳的运行状态,以最大程度发挥处理效能。而城镇污水处理厂进水水质的大幅度变化,会影响污水处理工艺的工况控制。污水处理工艺设计中,对于进水水质多采用统计分析不同日进水水质并选用一定保证率的方式确定。然而,在污水处理厂的实际运行过程中,受各种因素影响,进水水质即使在一天内也存在较大幅度的波动,甚至会出现瞬时进水水质超过设计水质的问题,这一波动对实际运行控制会产生极大影响。因此,对城镇污水处理厂进水水质变化规律进行研究分析,有助于生产运行调控决策,提高运行管理水平和出水达标保证率。笔者以广西壮族自治区某污水处理厂为例,分析进水水质波动周期性、主要水质指标相关性规律,并采用供水工程中时变化系数分析方法进行了研究。
1 研究材料与方法
1.1 研究材料
根据取样技术原理[1],数据变化周期决定采样频率。主要处理生活污水的城镇污水处理厂,其进水水质变化幅度多以小时为周期变化。2019年2月3日0时至12日9时,广西壮族自治区某污水处理厂进水中化学需氧量和氨氮浓度随时间的变化如图1、图2所示。数据取自在线监测仪,数据采集周期为2 h,采样点为污水处理厂进水泵房。污染物总量可根据污染物浓度与进水水量计算得到,并且生化处理系统污染物负荷采用每日污染物总量计算。分析进水水质波动程度时,采用每2 h累计污染物总量作为分析数据。
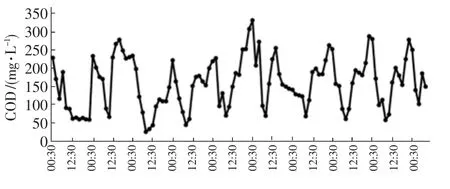
图1 化学需氧量的变化Fig.1 Change of chemical oxygen demand
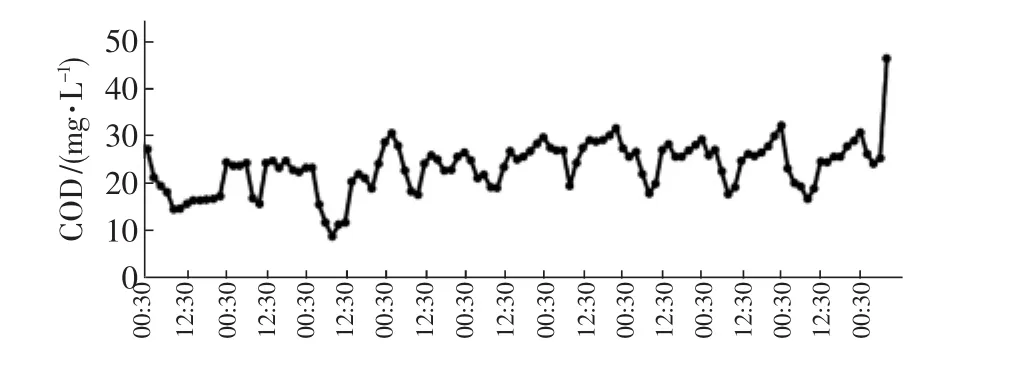
图2 氨氮的变化Fig.2 Change of ammonia nitrogen
1.2 研究方法
进水水质和水量数据本质上是一种信号流,因此可使用信号处理的方法研究其规律[2]。数据动态变化周期可以采用频谱分析方法[3],具体计算方法可采用离散傅里叶变换[4-5]。采用统计学中单参数Kolmogorov-Smimov检验判断进水水质变化是否符合正态分布[2],Spearman检验分析进水水质间相关性。采用供水工程中用水量变化系数分析方法,分析进水水质波动程度[6]。首先,按照0—24时顺序以每2 h为一组数据,计算污染物累计量(2 h累计)和百分数(占当日总量比例)。其次,计算当日污染物累计总量和平均每小时污染物累计量。最后,计算当日每小时污染物累计量最大值与平均每小时污染物累计量的比值,得到当日污染物时变化系数。
2 结果与讨论
2.1 进水水质统计分析
对进水化学需氧量和氨氮浓度数据进行单参数Kolmogorov-Smimov检验,分析其分布特性,结果如表1和表2所示。
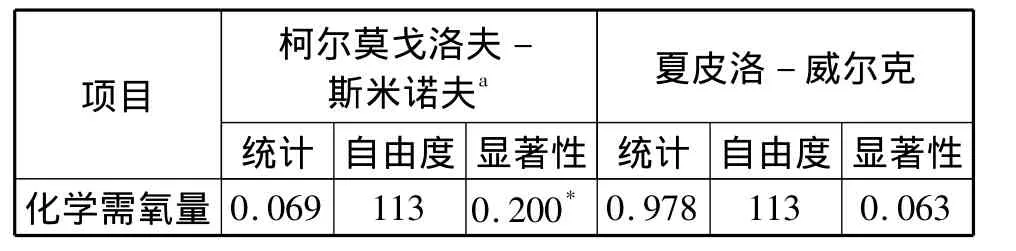
表1 化学需氧量的正态性检验Tab.1 Normal test of COD
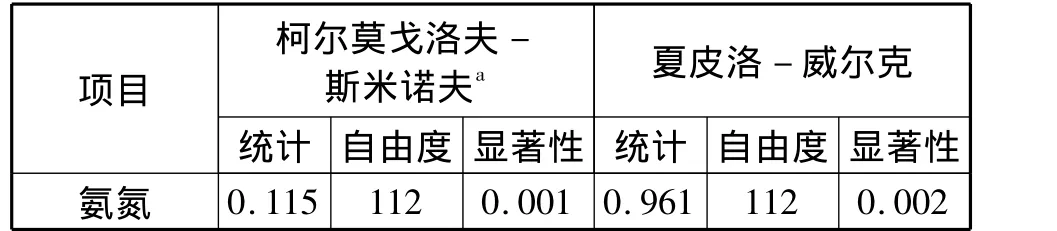
表2 氨氮的正态性检验Tab.2 Normal test of ammonia nitrogen
通过上述结果可知,进水化学需氧量的变化服从正态分布,氨氮则不服从正态分布。生活污水排放受多种因素影响,各类污染物具有一定的随机性规律。而氨氮则不遵循此规律,可能是受到非随机性氨氮排放源影响。
结合图1可以看出,虽然进水化学需氧量与氨氮的变化并非全部服从正态分布,但仍可能存在一定相关性。采用Spearman相关性检验,对进水化学需氧量与氨氮进行相关性分析,结果如表3所示。
结果表明,进水中化学需氧量与氨氮排放存在较为显著的正相关性,即化学需氧量与氨氮同步增加或同步减少,这一结果与生活污水中化学需氧量和氨氮均来自居民生活排放的同源性相符。另外,若生活污水排放源头存在碳氮比较低的问题,则这一情况在进入污水处理厂之前将不会获得明显改善,甚至随着碳源分解还会加剧,进一步影响总氮的去除。因此,对于来源较为稳定的生活污水,进水水质波动不会改善低碳氮比的问题。
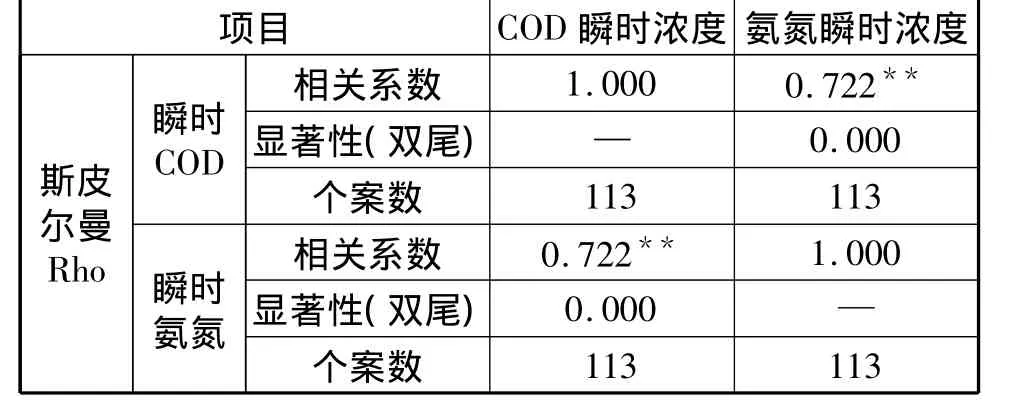
表3 化学需氧量与氨氮的相关性Tab.3 Correlation between COD and ammonia nitrogen
2.2 进水水质波动周期分析
对于该污水处理厂的进水水质,采用离散傅里叶变换对具有时间序列格式特征的数据(化学需氧量和氨氮)进行频谱分析,结果如图3、图4所示。
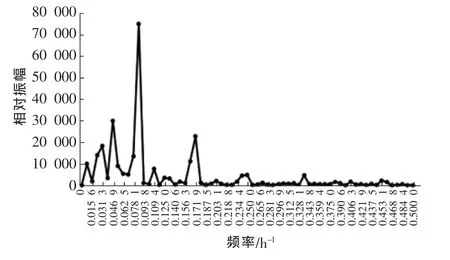
图3 进水化学需氧量的变化频谱分析Fig.3 Spectral analysis of the change of COD in influent
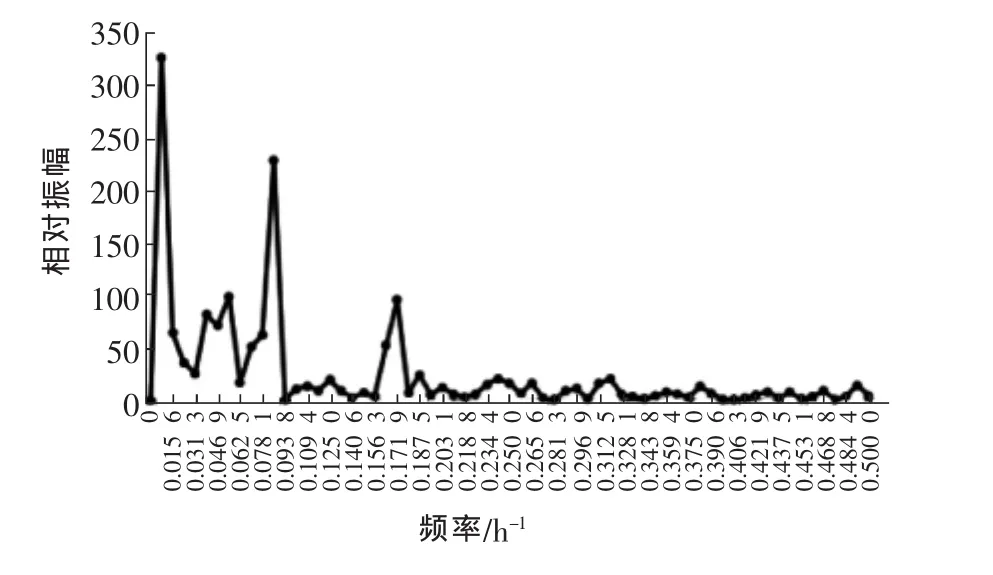
图4 进水氨氮的变化频谱分析Fig.4 Spectral analysis of the change of ammonia nitrogen in influent
进水化学需氧量波动最强频率为0.085 9 h-1,即周期为23.2 h,约为1 d。进水氨氮波动最强频率有2个,分别为0.007 812 5和0.085 937 5 h-1,即周期分别为256和23.3 h,对应约为11和1 d。由于该污水厂主要收集城镇居民生活污水,进水化学需氧量和氨氮的波动周期约为1 d,基本与城镇居民每日的生活规律相符。进水氨氮存在的11 d波动周期,这一结果可能与氨氮浓度不服从正态分布反映了相同的问题,即纳污范围内可能存在排放高氨氮废水的点源非随机(定期)向纳污管道排放。
2.3 进水水质波动程度分析
2.3.1 进水水质时变化分析
进水水质在一日内的波动程度较大,甚至存在部分瞬时进水水质达到或超过设计水质的现象,对系统稳定运行产生较大影响。2月4—10日,COD的日累积总量分别为9 020.00,3 986.51,5 710.83,10 552.80,12 277.22,12 111.26 和 9 577.97 kg,平均 量 分 别 为 375.83,166.10,237.95,439.70,511.55,504.64和399.08 kg/h,每 2 h的变化和时变化系数k的分析结果见图5。
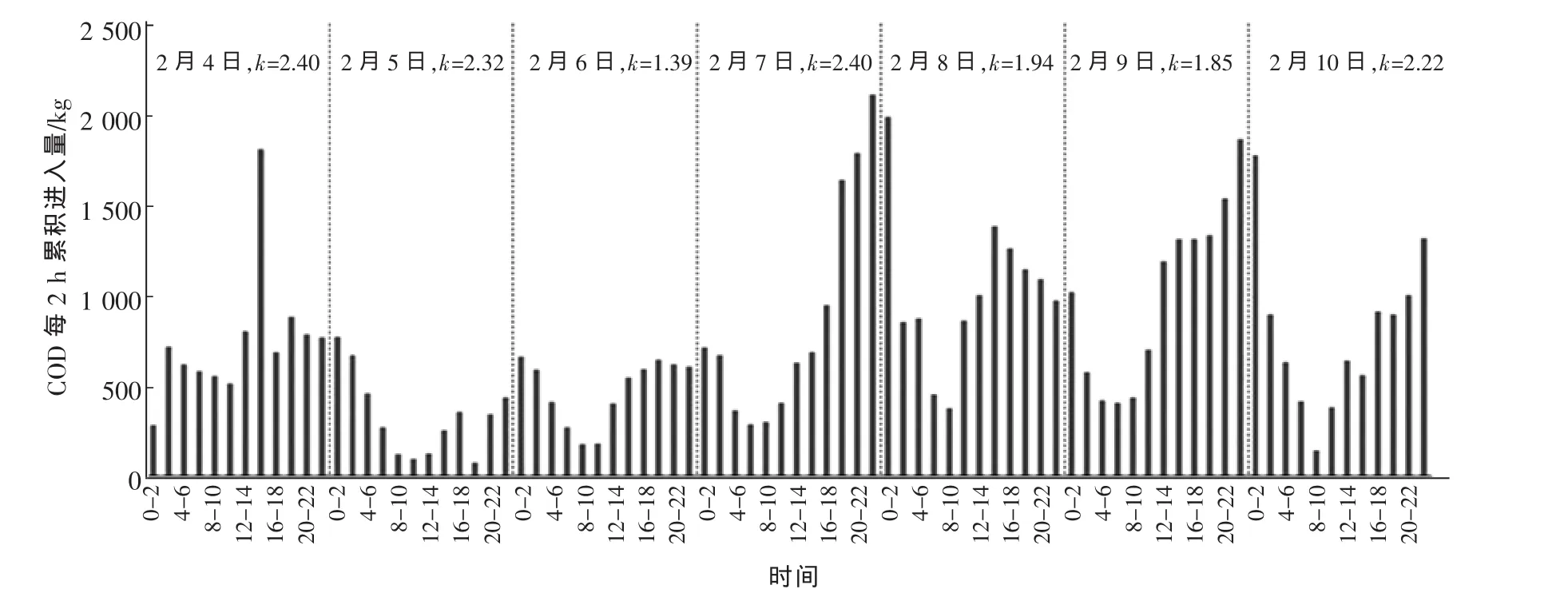
图5 进水化学需氧量的变化Fig.5 Change of COD in influent
2月4—10日,氨氮的日累积总量分别为1 072.21,628.06,978.96,1 356.73,1 739.05,1 780.55和 1 389.71 kg,平均量分别为 44.68,26.17,40.79,56.53,72.46,74.19 和 57.90 kg/h,进水氨氮每2 h的变化和时变化系数k的分析结果见图6。
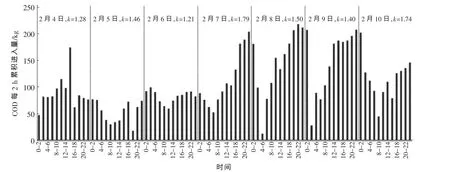
图6 进水氨氮变化曲线Fig.6 Change of ammonia nitrogen in influent
进水化学需氧量和氨氮量均存在较大程度波动,其中化学需氧量进水量时变化系数在1.39~2.40,每日22:00至次日2:00出现峰值,每日6:00至12:00出现谷值;氨氮进水量时变化系数在1.21~1.79,每日22:00至次日2:00出现峰值,每日4:00至12:00出现谷值。化学需氧量和氨氮的峰值与居民生活晚间排水高峰期,谷值与居民生活早间排水较少的规律相符。该厂在实际生产运行中,应特别在峰值时段(每日22:00至次日2:00)对处理工艺运行进行对应的调整。另外,进水化学需氧量和氨氮存在较大波动,对该厂进行技术改造时应充分考虑水质的波动。
2.3.2 化学需氧量与氨氮比值变化分析
在进水水质出现谷值时(每日4:00至12:00),可降低处理工艺的处理负荷。但对于较难去除的总氮,进水化学需氧量的降低可能导致出现有机碳源匮乏的问题。脱氮碳源评价多采用进水生化需氧量与进水总凯氏氮的比值。对于稳定的生活污水而言,其组成相对固定。同时,污水处理厂进水水质在线监测无法实现生化需氧量检测,获得总凯氏氮实时数据。因此,采用进水化学需氧量与氨氮的比值(化学需氧量每2 h累积进入量/氨氮每2 h累积进入量),分析进水生化需氧量与进水总凯氏氮比值的变化趋势,结果如图7所示。
图7 进水化学需氧量与氨氮比值的逐时(2 h)变化曲线Fig.7 Hourly(2 h)change curve of the ratio of COD to ammonia nitrogen in influent
结果表明,进水化学需氧量与氨氮比值每日呈现一定规律变化,每日最大值多出现在22:00至次日2:00,最小值多出现在8:00—12:00。该比值的变化规律与每日化学需氧量和氨氮的变化规律基本相符,这一现象也与城镇居民生活规律相符。这也说明在居民生活排水较少的时段,脱氮所需的碳源最为匮乏,处理工艺需要进行相应调整或人工补充碳源。
3 结论
① 主要处理生活污水的城镇污水处理厂,进水中的化学需氧量服从正态分布,符合其排放来源排放随机性规律。进水氨氮不服从正态分布,说明有非随机性排放点源对其造成干扰。进水化学需氧量和氨氮具有相关性,符合两者同源性(均来自居民生活排放)规律。
② 城镇污水处理厂进水化学需氧量和氨氮的波动周期约为1 d。进水氨氮出现约11 d的波动周期,推断存在排放点源对其产生干扰。
③ 进水化学需氧量、进水氨氮以及两者的比值均在每日22:00至次日2:00出现最大值,在每日8:00(4:00)至12:00出现最小值,与居民生活污水排放规律相符。应在排放高峰期与排放水量较少的时段,分别注意对处理工艺曝气量、总氮去除工况进行相应的调整。
④ 进水化学需氧量、进水氨氮的时变化系数分别为1.39~2.40和1.21~1.79,进水水质每日逐时存在较大波动,对该类污水厂开展技术改造时应特别注意。

