自适应模型预测控制的车道保持控制策略

万远航， 邵毅明， 胡广雪， 吴文文

(1. 重庆交通大学 交通运输学院， 重庆 400074；2. 重庆交通大学 机电与车辆工程学院， 重庆 400074)

车辆行驶安全和交通拥堵作为当今交通系统的主要问题，在给人们出行造成困扰的同时，也推动着车辆主动安全技术的快速发展[1-2].车道保持作为主动安全技术之一，根据感知驾驶车辆与道路中线偏差，求解对应控制序列，以此实现车辆道路中线稳定跟随,不但能降低驾驶负荷，防止驾驶分心，还具有实现路线最优的潜力[3].控制算法是决定车道保持系统整体性能的关键因素，传统车道保持系统采用PID[4-5]、滑膜控制[6-9]、线性二次最优控制[10-13]等算法控制，一定程度上能够改善行车安全，但缺乏对车辆安全约束及参数不确定性的处理能力.模型预测算法具有天然的多模型约束处理优势，能够较好地结合规划控制、感知层面中的传感信息，是无人驾驶车辆控制过程中体现车辆运动学和动力学约束的理想方法[14-15].传统模型预测控制(MPC)虽然解决了系统不确定下的递归约束问题，但由于各控制时域下车辆模型参数恒定，强非线性工况下仍难以保证良好的鲁棒性，进而降低了系统整体工作性能.因此，本文在传统模型预测控制算法的基础上，利用辛普森法则，调整各控制时域车辆模型，补偿其非线性时变特性，并在Simulink环境下设计对应的仿真工况，同时验证所设计控制器的整体性能.

1 车道保持系统建模

1.1 车辆侧向动力学模块

车辆侧向动力学模块采用单轨模型，具体表征方程为

(1)

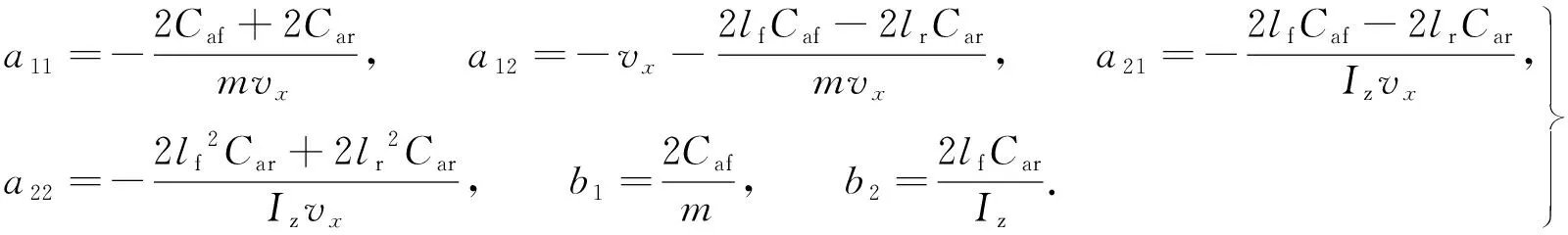
(2)

式(1),(2)中:ψ为车辆横摆角；δ为前轮转角；y为车辆的侧向位置；Caf，Car分别为前、后轮侧偏刚度；lf，lr分别为质心距前、后轴的轴距；Iz为车辆的转动惯量；vx为车辆的纵向速度.

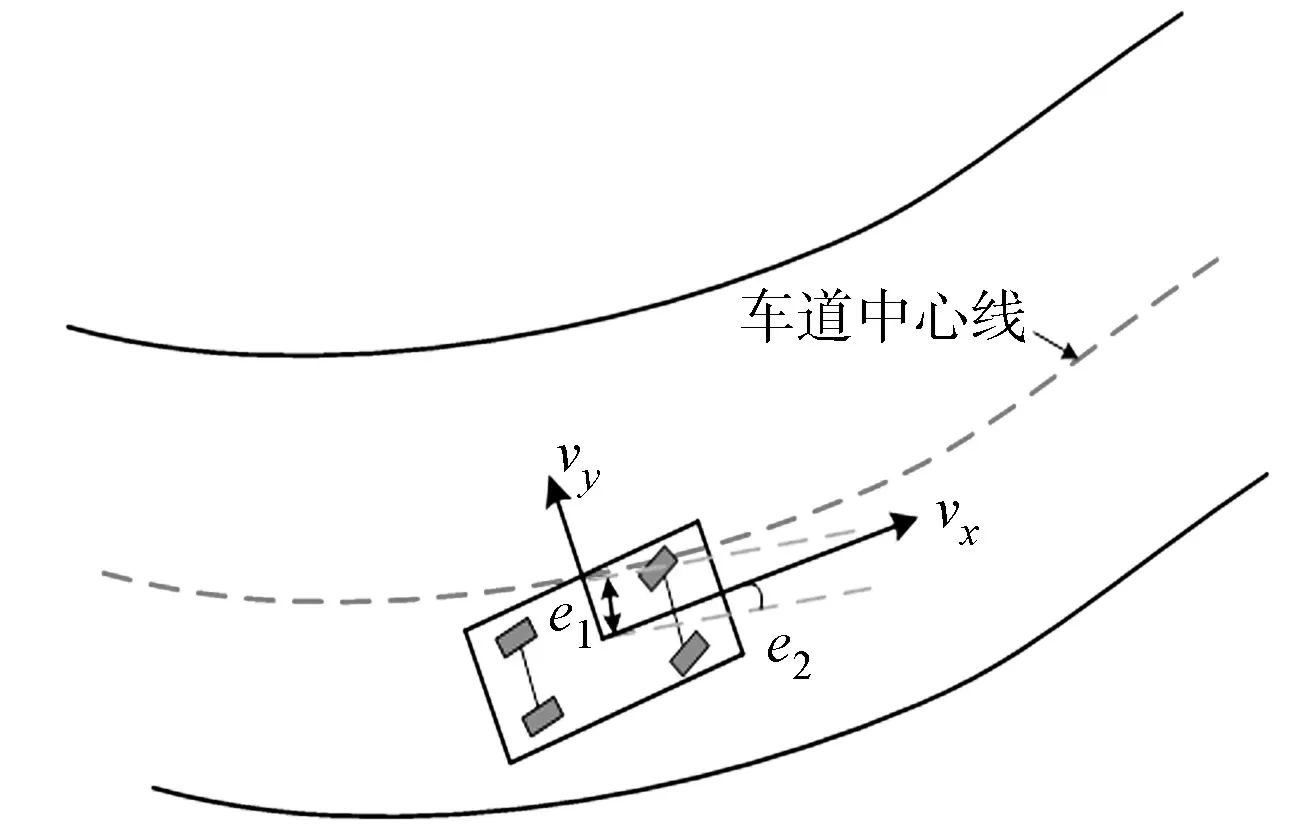
图1 车辆传感模块示意图Fig.1 Schematic of vehicle sensing module

1.2 车辆传感模块

构建传感模块模拟摄像头感知，并计算车辆与道路中心线之间的侧向位移偏差e1及横摆角偏差e2.车辆传感模块示意图，如图1所示.图1中：vy为车辆的侧向速度.

对式(1)进行扩展，建立以道路曲率、纵向速度、侧向速度、横摆角速度为输入，侧向位移偏差和横摆角偏差为输出的传感模块，即

(3)

式(3)中:ρ为道路半径曲率;r为横摆角速度.

1.3 道路曲率预瞄模块

曲率预瞄模块利用道路信息，根据当前时间及预瞄长度，计算并输出当前道路曲率及未来道路曲率序列.文中道路曲率预瞄模块设置为提前1 s输出，由于仿真步长Ts为0.1 s，故提前10个步长进行输出.相邻道路曲率采用数值梯度gradient函数求解，即

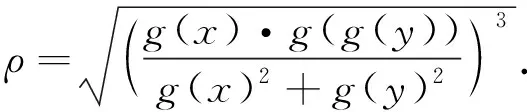
(4)

1.4 连续时间预测模型

结合式(1)～(3)，通过引入时间常数τ近似表征车辆纵向动力学，以道路曲率和纵向速度的乘积作为测量扰动，并采用白噪声ωod模拟未测量扰动，车辆连续时间预测模型描述为

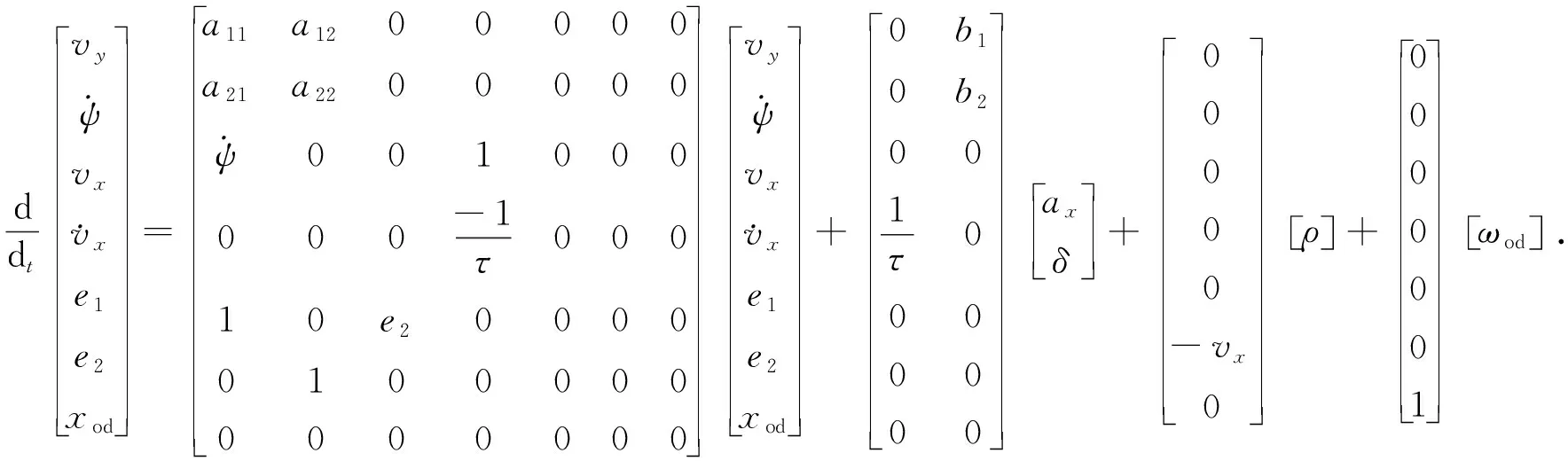
(5)

式(5)中:ax为车辆的纵向加速度；xod为输出干扰，即未测量扰动.

2 自适应MPC车道保持控制算法

车辆高速行驶过程中伴随强耦合、高非线性特征，传统MPC内部模型固定，难以在车辆行驶工况转换中具备良好的控制稳定性.为改善行驶过程中的非线性问题，采用自适应MPC算法，在各控制周期根据当前行驶工况调整车辆预测模型，以此提高车道保持行驶的安全性和稳定性.

对式(5)车辆预测模型进行离散化，MPC框架下所得到的车辆状态方程可描述为

x(k+1)=Acx(k)+Bcu(k)+Bvv(k)+Bdd(k)，y(k)=Cx(k)+Dvv(k)+Ddd(k).

(6)

式(6)中:矩阵Ac,Bc,Bd,Bv,C,Dv,Dd为随时间变化的参数矩阵；x为系统状态量；u为系统控制量；v为输入测量干扰;d为未测量干扰;变量k为当前控制时刻；y为系统输出量.

在保证控制周期与仿真步长相同、系统输入输出为常量的前提下，采用连续化线性方法，根据Simpons法则，通过expm函数实现内部模型矩阵的更新.矩阵Ad,Bd可描述为

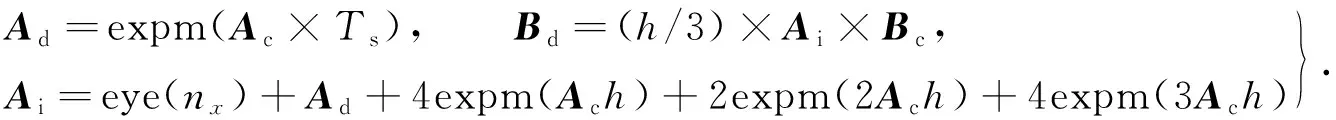
(7)

式(7)中:Ai为单位步长各分段对应的状态矩阵;h为单位步长各分段时长,h=Ts/4;nx为状态量维度.

根据每个控制周期更新的操纵点及车辆模型信息，利用参考系统信息与当前系统信息偏差设计增量式模型，模型可描述为

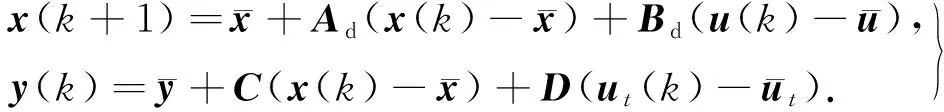
(8)

车道保持过程中，通过最小化车辆侧向位移偏差、横摆角偏差及驾驶人期望速度偏差，实现车辆驾驶期望稳定跟随.考虑到车辆自身动力性能、物理转向限制及行驶过程中的稳定性，分别对车辆纵向加速度、前轮转角范围及变化率设置控制极限约束，具体表现为

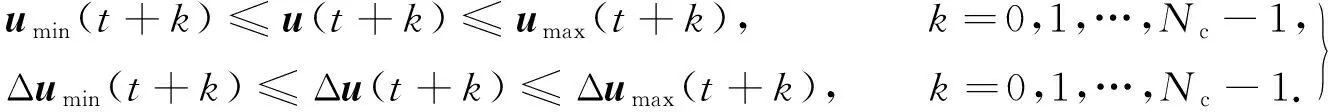
(9)

求解过程中，为保证控制量求解连续性，目标函数引入松弛变量增强系统可行解，具体表现为

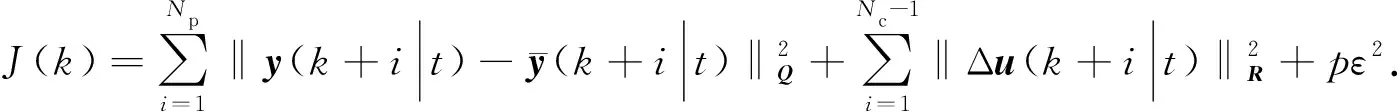
(10)

式(10)中:Np为预测时域;p为权重系数；ε为松弛因子；Q,R为权重矩阵.

在目标函数输出变量输出权重指定过程中，由于仅有两个操纵变量，难以同时实现零稳态偏移，设置横摆角偏差权重系数为零，即稳态工况下侧向位移偏差为零时，默认车辆横摆角无偏差.随后，车道保持系统控制器根据各控制周期更新的车辆模型、目标函数及对应的约束，利用Optimization Toolbox工具箱求解出对应的控制序列，即ΔU=[Δut，Δut+1，…，Δut+Nc-1，ε]T.

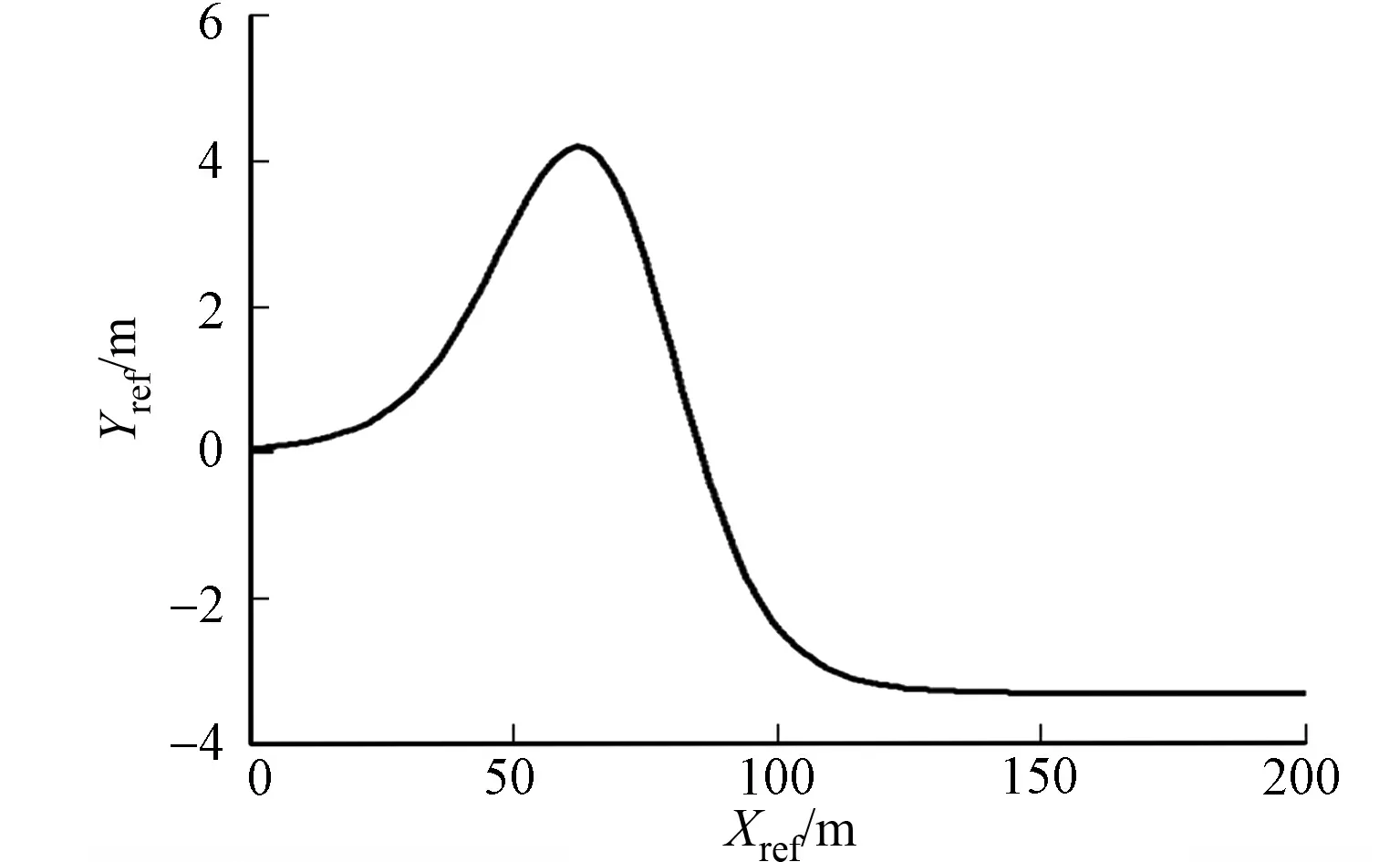
图2 双移线参考轨迹Fig.2 Double shift line reference track

将控制序列第一个元素作为控制增量输入系统，进入下一控制周期，不断重复该过程，以此实现车道保持的MPC转向控制.

3 仿真结果及分析

为验证所设计的基于自适应MPC算法的车道保持系统，在Matlab环境下开展仿真试验，并与基于传统MPC算法的控制器进行对比.采用双移线工况检测车道保持系统跟踪精度和行驶稳定性.双移线参考轨迹，如图2所示.图2中：Xref，Yref分别为横向、纵向参考轨迹.仿真车辆参数，如表1所示.表1中：m为整车质量；Ix为横摆转动惯量.设置车辆初始车速为20 m·s-1，期望车速为25 m·s-1，控制时域Nc为2，预测时域Np为10，开展双移线工况仿真.

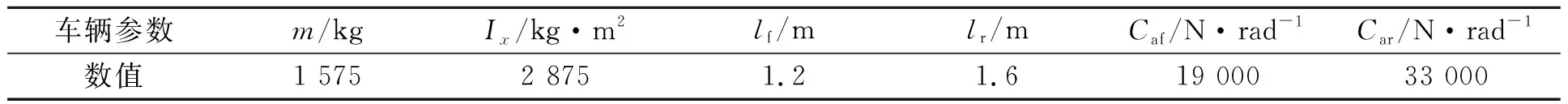
表1 仿真车辆参数Tab.1 Simulation vehicle parameters

两种算法控制下的车道保持仿真结果，如图3所示.图3中：t为时间.

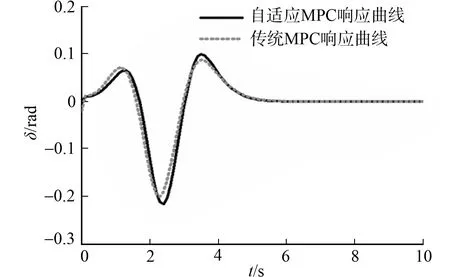
(a) 前轮转角

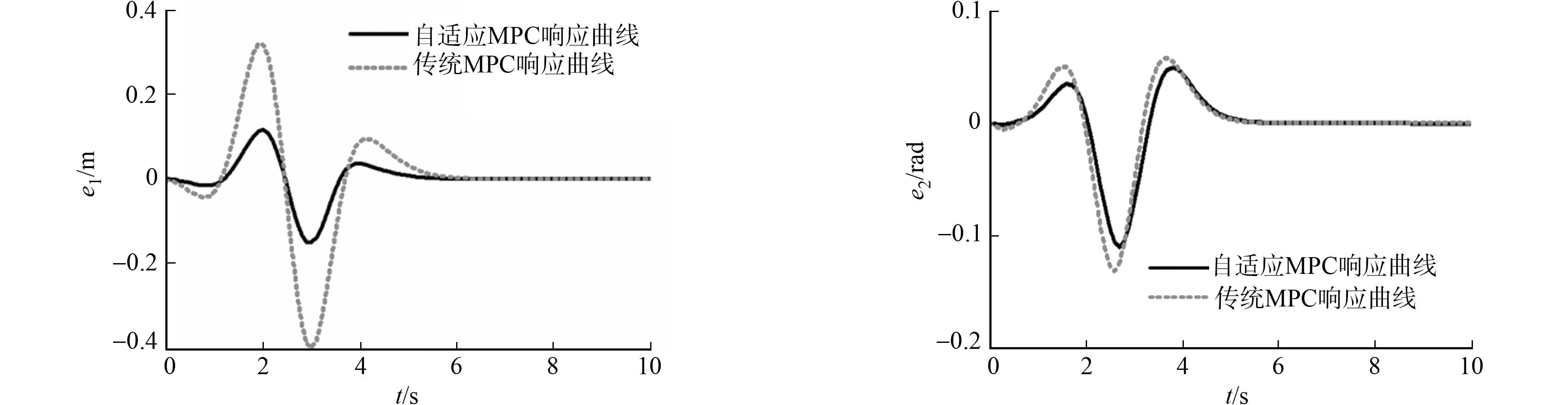
(b) 侧向位移偏差 (c) 横摆角偏差图3 两种算法控制下的车道保持仿真结果Fig.3 Simulation results of lane keeping under two control algorithms

由图3(a)可知：车辆在保持道路中心线行驶过程中，由于产生了侧向位移偏差和横摆角偏差，控制器逐步求解并输出相应的前轮转角控制量调整车辆行驶姿态，从而减小车辆行驶过程中产生的侧向位移偏差和横摆角偏差，直至车辆驶出弯道，前轮转角回归正常位置.由图3(b)，(c)可知：车辆车道保持过程中，自适应MPC车辆的侧向位移偏差和横摆角偏差分别为[-0.15 m，0.11 m]，[-0.11 rad，0.30 rad]，传统MPC控制车辆的侧向位移偏差和横摆角偏差分别为[-0.40 m，0.32 m]，[-0.13 rad，0.05 rad]，两种控制算法均能保证车道保持行车安全，主要得益于MPC算法在各采样时刻对系统未来状态进行预测，并优化转向过程的性能指标，能够在车道保持过程中维持良好的动态响应.

对比两种控制算法响应曲线可以发现:基于自适应MPC的车辆在车道保持行驶过程中具有更小的侧向位移偏差峰值及横摆角偏差峰值，相较于传统MPC下降了62.5%，15.3%，说明采用自适应MPC算法的车道保持系统更具安全性，主要原因在于自适应MPC在各控制周期对车辆模型进行更新，提高了模型预测精度，增强了车辆强非线性工况下的鲁棒性，从而保证了系统良好的工作性能.

此外，车辆舒适性能也可以通过车道保持仿真结果(图4)进行比较.图4中：v为车辆速度.由图4可知：相较于传统MPC算法，采用自适应MPC算法得到的车辆速度和纵向加速度响应曲线都更为平滑，说明自适应MPC的车道保持控制过程中，在保证行车安全前提下，可以获取更好的行驶舒适性.

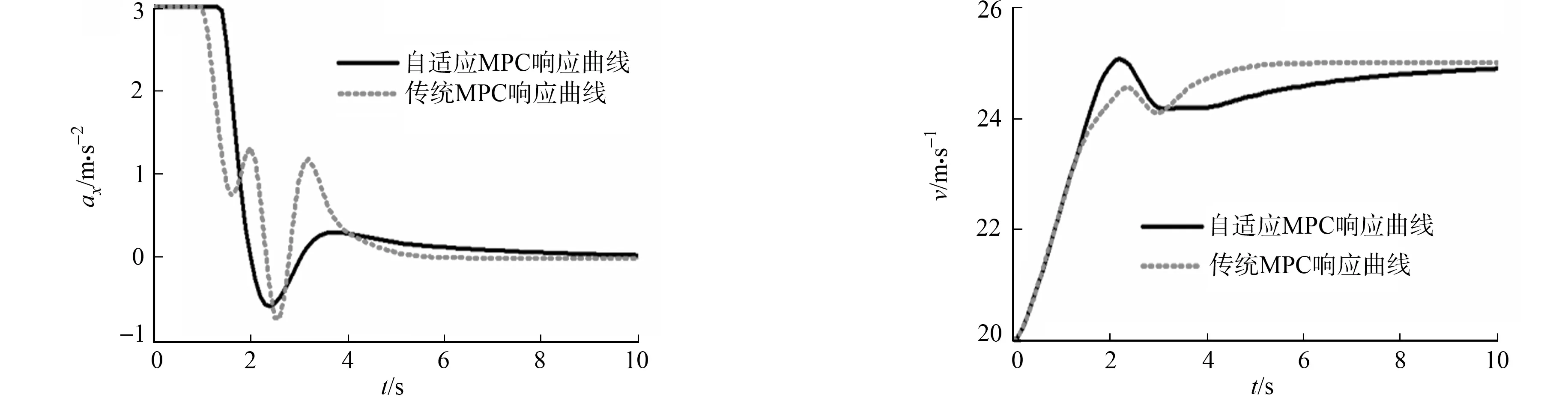
(a) 纵向加速度 (b) 车辆速度图4 车道保持仿真结果Fig.4 Lane keeping simulation results

4 结论

针对车道保持系统控制存在的强非线性问题，联合车辆动力学模块、车辆传感模块、道路曲率预瞄模块，建立车辆连续时间预测模型，在传统MPC算法的基础上，结合Simpons法则，设计基于自适应MPC的转向控制策略，并通过仿真试验对该控制器进行验证，其仿真结果如下.

1) 无论传统MPC算法还是自适应MPC算法，得益于MPC算法自身特性，均能实现车辆车道保持行车安全.

2) 相较于传统MPC，自适应MPC在各控制周期能够实现车辆模型更新，在强非线性工况下具备更好的鲁棒性，故能在保证行车安全的前提下，获取较好的乘坐舒适性.