一种改进人工鱼群算法求解冷链中车辆路径问题
李俊青 黄体浩 宋美娴 韩玉艳
(聊城大学 计算机学院,山东 聊城 252059)
0 引言
车辆路径问题(Vehicle Routing Problem,VRP)是现实生活中最重要的问题之一,现已成为运输、供应链管理和物流领域的核心问题.它有众多的实际应用其中包括公交路线规划、邮政、包裹运送、餐饮配送、银行和ATM终端的现金配送、工业垃圾收集等.在为给定的配送问题构建规划路径时,需要考虑大量的实际问题,例如可用的车队规模、容量、地理上分散的客户之间的行程成本,可能拜访客户的时间间隔,以及许多其他意外情况,这些因素都有可能影响路径规划的可行性.
随着时间窗和其他时间数据的进一步复杂化,带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)应运而生.Solomon等人对VRPTW进行了较早的研究,并于1992年提出了一种新的优化算法,通过列生成策略解决了VRPTW集划分公式的LP松弛问题[1].近年来,多种元启发式算法被成功应用于求解VRPTW问题中,典型的包括:粒子群算法[2]、细菌觅食优化算法[3]、人工蜂群算法[4]等.
随着人们对冷藏食品需求的不断增加,冷链物流作为新兴的物流方式逐渐受到人们的重视.在一些文献中将冷链配送问题与VRPTW问题结合起来,其中惩罚成本是反映冷链时间敏感性的主要因素.2007年,Hsu等人考虑了在易腐食品运送过程中设备能耗以及时间窗约束对配送的影响[5].2014年,Hsu和Chen进一步研究了根据不同温度区域的要求优化多温度食品制备的车辆大小和配送调度[6].2015年,Ji等人针对冷链物流中同时取货配送(Vehicle Routing Problem with Simultaneous Pickup and Delivery,VRPSPD)的车辆路径问题,分析了冷链物流配送过程中车辆固定成本、运行成本、冷藏成本和冷链货物变质成本等成本结构,建立了VRPSPD问题优化模型[7].2019年,Li等人从温室气体排放的角度出发,研究了冷链物流绿色车辆路径问题,建立了冷链物流的绿色车辆路径优化模型[8].2019年,Zhang等人将低碳经济引入冷链物流,建立了包含碳排放成本的冷链物流路径优化模型,使用核糖核酸计算与蚁群算法相结合的方法进行求解,并将其应用到雄安某冷链物流企业的路径优化问题中,得到了较好的结果[9].Qin和Tao等人考虑了成本、客户满意度和碳排放等影响因素,建立了以单位满意顾客成本最小为目标函数的综合冷链车辆路径优化问题模型[10].
综上所述,车辆路径问题及其变体在国内外都有着广泛的研究,不仅对问题本身的研究特别是基本的VRP问题及其符合现实情况的变体进行了研究,也对该类问题的求解算法进行了研究与优化.随着时代发展,所考虑的问题不仅是单一需求,而需要将更多的因素纳入考虑范围,如配送车型的多样化、时间窗的选择等.但是关于冷链运输同时考虑顾客满意度、能量消耗和碳排放三个因素的研究还较少.因此,在激烈的市场竞争和低碳经济的需求下,冷链物流为了更好的发展,配送网络不仅要考虑项目的总成本,还要必须关注客户满意度和碳排放,不断优化问题模型,在为客户提供更好更快服务的同时获得利益的最大化,这不仅是现代企业的要求也符合社会发展的趋势.
1 问题描述
在传统VRP问题中,所有车辆的类型都是相同的,即每辆车都有同样的能源消耗,装载能力与运送装置.然而在现实的物流系统中,许多配送车辆的类型、装载能力、能耗指标和运送装置都是不同的.因此本文研究的问题可以描述为:有一个配送中心可以为客户提供常温货物与冷冻货物,有一定数量的运输车辆,车型也有常温与冷藏两种,服务于一组客户.配送中心和客户的具体信息都是确定不变的,如客户的位置、所需数量、需求车型等.另外,每个客户点都有两种时间窗:最优时间窗和松弛时间窗,如果服务车辆在客户点的最优时间窗口内到达,客户将完全满意;如果在客户规定的松弛时间窗内到达,则需要根据车辆到达的时间计算客户满意度.因此,本文的主要目的是在考虑成本、客户满意度和环境因素的情况下找到最优的解决方案.具体约束条件如(1) 车辆分为常温车型与冷藏车型,每条路线的总负荷不得超过车辆的额定负荷,(2) 配送中心和客户点的具体位置已知,(3) 每个客户的需求货物种类与数量已知,(4) 完成配送任务后,所有货车必须返回配送中心,(5) 每个客户只服务一次,(6) 服务车辆的车型要与客户要求的车型一致,(7) 运输过程不考虑道路拥堵、天气原因等状况.
1.1 问题建模
(1) 集合.H={1,…,k}:可用车辆类型的集合,V={0,1,…,n}:节点集合,节点0代表配送中心,[1,…,n]代表客户点,V'=V{0}.
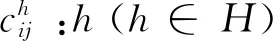
(3) 决策变量.
1.2 成本分析
(1) 固定成本C1.当使用车辆时,需要支付一些固定的费用,包括司机的工资、卡车的损耗、道路维护费用等等,由于每种车型的固定成本是不同的.因此在该模型中车辆的固定成本C1可以表示为
(1)
(2) 运输成本C2.车辆的运输成本主要与燃油消耗、维护保养等因素相关,与车辆行驶距离成正比
(2)
(3) 制冷成本C3.制冷成本公式可以表示为
(3)
(4) 碳排放成本C4.在运输和配送过程中,碳排放主要产生来源有两个:运输途中燃料的排放和设备制冷产生的气体排放.在本文中,燃料消耗在每单位距离的线性函数公式ρ(X)计算公式如
(4)
因此,运输过程中的碳排放量表示如
(5)
HVRPTW模型的碳排放成本公式为
(6)
(5) 货损成本C5.公式D(t)=D0e-∂t可以计算货物的损失成本
(7)

1.3 问题模型
在本文中对冷链中带时间窗与顾客满意度的研究建立了以下多目标优化模型
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
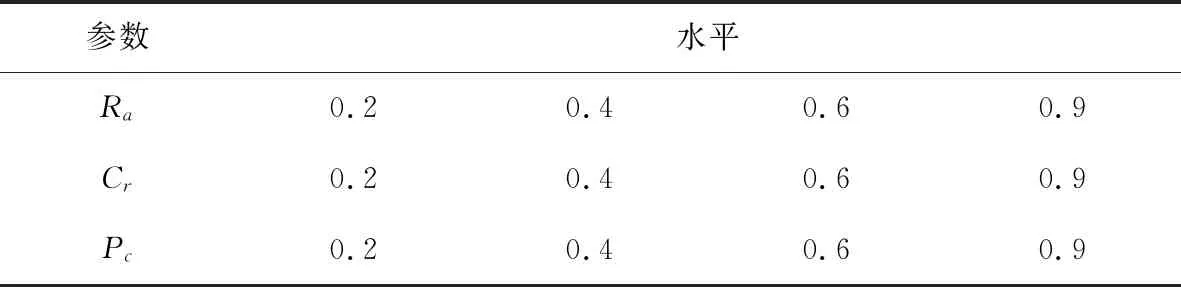
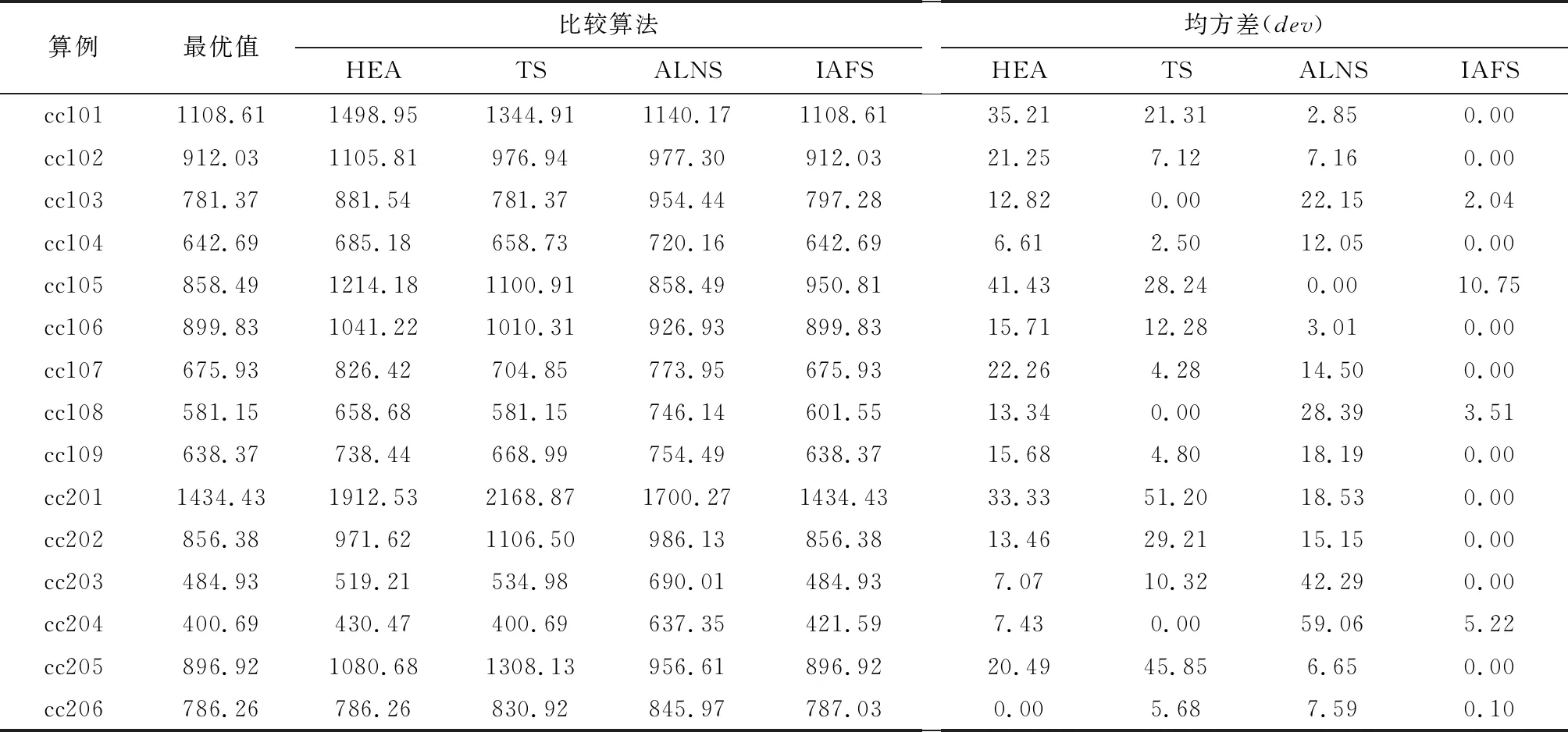
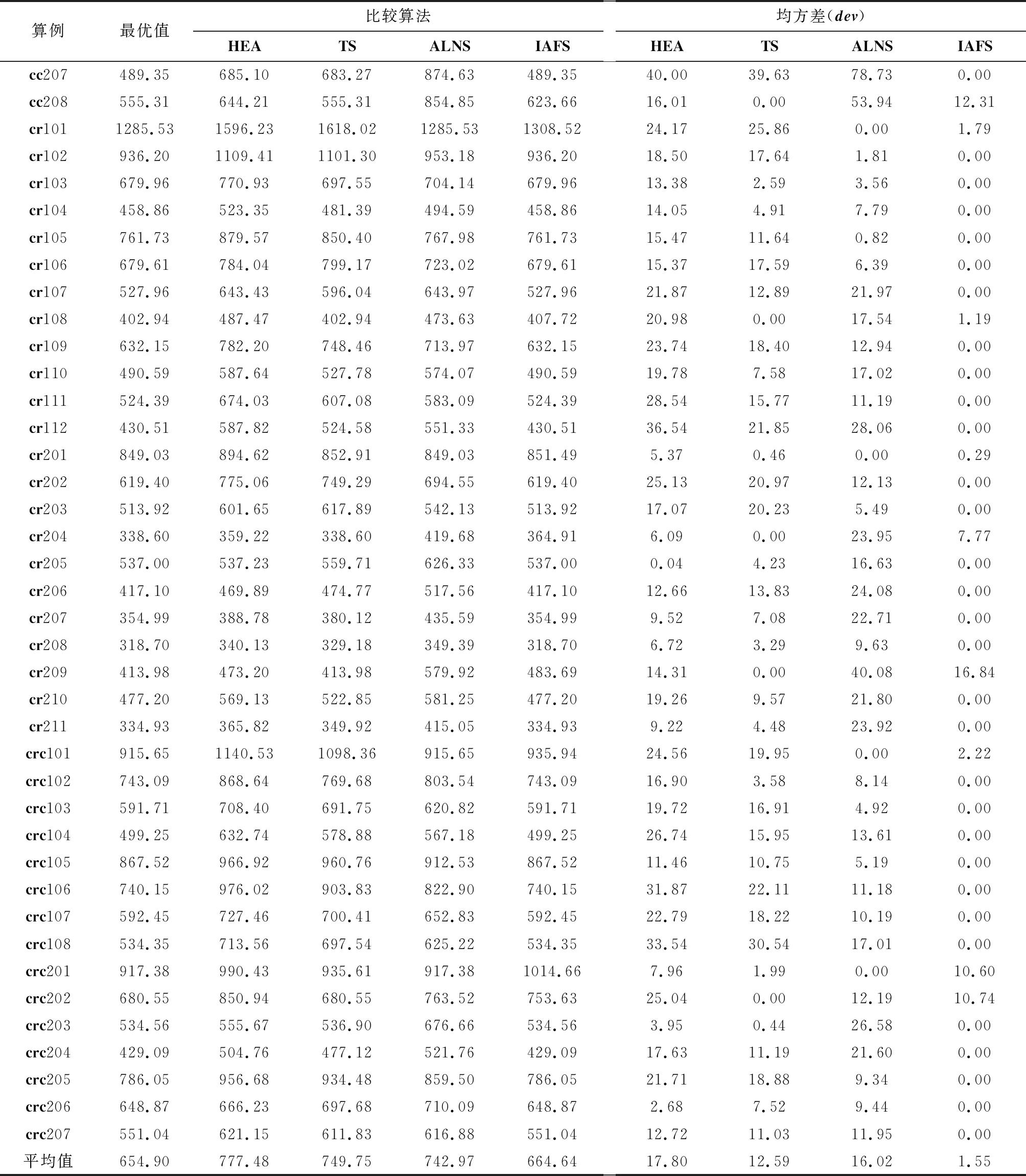
EEti≤ti (17) (18) t0=0, (19) (20) (21) 约束条件(9)表示每种类型使用数量不能超出该车型的最大数量.约束条件(10)和(11)保证客户点只被访问一次.约束条件(12)每辆车必须离开车场.约束条件(13)保证车辆在服务完后前往下一个客户点.约束条件(14)和(15)表示物品的流动关系.约束条件(16)保证在每条路线上h型车辆总的装载量不超过Qh.约束条件(17)保证车辆不违反客户的时间窗.约束条件(18)和(19)表示客户点的时间关系.约束条件(20)和(21)限定了变量取值范围. 人工鱼群(Artificial Fish Swarm,AFS)算法是李晓磊于2002年在其博士论文中提出的,是一种基于简化的鱼群自然社会行为的模拟和群集理论[11].人工鱼群算法有很多优点:算法结构简单,只使用目标的函数值作为决策数据;计算速度快,即使有随机因素的存在,算法也能快速计算出最佳位置. 人工鱼群算法的优化过程是通过多种基本行为来实现的,主要包括3个步骤:(1) 生成一组初始人工鱼群,构造初始种群解;(2) 每条人工鱼都会经历以下四种行为:觅食、聚群、追尾和随机行为,以获得更好的位置与较高的食物浓度;(3) 使用公告板解决方案记录到目前为止找到的最佳解决方案. 在经典的AFS算法中,可以初始化m个点,即m条人工鱼X=(x1,x2,…,xm)用来识别有希望寻找全局解决方案的区域,其中xi为当前鱼状态.Yi=f(xi)为所在位置的食物浓度.人工鱼个体i与j之间的距离用dij=‖xi-xj‖表示.AFS算法的关键问题是每条人工鱼的感知距离,也被称为“可视范围”,用Visual进行表示.Step表示人工鱼移动的最大步长.δ为拥挤度因子,δ∈(0,1).Try_number为人工鱼的最大试探次数 xv=x+Visual·Rand(), (22) (23) Rand()函数用于生成0到1之间的随机数. 在经典AFS算法中,觅食行为用于生成当前人工鱼“可视范围”内的邻域解.假设xi为当前人工鱼状态,如果邻域内存在另一条人工鱼,其状态为xj,同时食物浓度Yi (24) 假设为当前人工鱼xi,在其“视野范围”内的伙伴数目nf和中心位置xc,若Yc/nf>δYi,则表明中心位置有足够的食物且不拥挤,同时Yi (25) 人工鱼xi可以在“可视范围”内选择其他人工鱼如最优位置的人工鱼,然后利用Ybest=f(xbest)计算最大食物浓度.在追尾行为中,xi位置状态更新公式如 (26) 当人工鱼xi的“可视范围”为空(没有其他的人工鱼可以追随)或其他行为未执行时,人工鱼xi会随机寻找另一个有食物的区域. 在本节中,提出了一种改进的人工鱼群算法(Improved Artificial Fish Swarm,IAFS)来解决冷链物流中的HVRPTW问题.为了设计AFS算法的离散维数,将算法的所有步骤都进行了离散化,包括编码和解码方法、初始化方法和经典AFS算法的改进行为. 本算法考虑了问题的特点和目标,采用二维数组的方式编码一个解,二维数组的第一维表示每一辆车,第二维表示每辆车服务客户的序号和顺序.例如,车队包含8个客户,两种车辆类型,每种车型都有25辆车.第一类是没有任何特殊装置的常温车型,第二类是装有冷藏装置的车型,图1给出了一个编码示例.每辆车都由一个数组表示,数组中包含该车辆服务的客户序列,客户序号的先后顺序表示这些客户点的服务次序.对于给定的8个客户,将5个客户{2,5,6,7,8}分给第一类车辆(常温车),将{1,3,4}分配给第二类车辆(冷藏车).然后按照顺序将{2,7,6}分配到同一辆车上,将{5,8}分配到相同类型的另一辆车上. 对于3.1小节中的编码,解码如甘特图2所示,将所有客户点逐一分配到相应的车辆上.同时,在解码过程中需要考虑两对客户之间的距离、每个客户接受服务的最早和最晚时间,客户的满意程度,每个客户的服务时长、车辆容量、以及每辆车的最大装载能力.同时,在解码过程中,最重要的任务之一是计算客户满意度,并将其加入到问题目标函数中. 在经典的AFS算法中,觅食行为用于为每个选择的解生成邻近解.然而,AFS算法中的觅食行为仅适用于连续优化问题,为了使其适用于求解离散优化问题,提出了一种改进的觅食行为,具体如:Step 1:循环初始解集的每一个解xi,根据“可视范围”确定解的邻域解集.Step 2:如果当前解xi在“可视范围”内随机选择一个解xj,xj如果的目标值比xi优秀,则xi向xj方向移动,即xi与xj进行交叉操作.Step 3:在公告板更新最好解.Step 4:更新xi的尝试次数Try_number.在改进的觅食行为中,对现有的人工鱼xi采取两种策略:(1) 策略I. Step 1:为了生成邻域解,随机选择一种车型,对所选车型随机选择一辆车,然后从中随机选择一个客户,并将其在所选车辆中删除.Step 2:将所选客户插入到同类型的另一辆车中.在策略I中,将客户插入到当前解决方案的时间复杂度为O(n2),假设要重新插入的客户数量为(1/r)×n,其中r为选择的速率,则该策略的时间复杂度为O(n3).(2) 策略Ⅱ. Step 1:为了生成邻域解,与策略I相同,随机选择一辆车,然后从所选车辆中随机选择一定数量的客户并将这些客户从当前车辆中删除.Step 2:将选择的客户随机插入到相同车型的其他车辆中.策略Ⅱ中的改进的觅食行为过程如图3.两种觅食启发式在该改进算法中是随机选择使用的. 在经典的AFS算法中,追尾行为是使当前的解决方案从相邻的解决方案中学习以增强算法收敛的快速性和全局性.在经典的追尾行为中,如果“可视范围”内不拥挤,且中心点在“可视范围”中具有最佳的目标函数值,则趋向于中心点移动.然而,典型的AFS算法是针对连续优化问题的,为了使AFS算法更适应于求解离散的优化问题,提出了离散追尾行为.在改进的追尾行为中有以下两种交叉方式. 第一种改进交叉:主要思想是删除其他父代个体中路线上出现的客户,然后将它们插入到当前父代个体最佳位置形成新的解决方案.具体步骤:(1) 随机选择两个父代解p1、p2;(2) 从p2中选择一定数量的车辆,并将这些车辆上的客户存储到集合D中;(3) 将D中的所有客户从p1中删除,利用PFIH启发式将这些被删除的客户插入到最优位置. 图4显示了p1和p2交叉的过程.首先,从p2中按一定比例选择了一些客户,一共10个客户,被选择的客户数量为1/m(m=2),即5个客户.将这5个客户从p1的路径中移除,然后重新计算最佳插入位置,将客户插入到p1中.交叉的时间复杂度为O(n). 第二种交叉的步骤:(1) 随机选择两个父代解p1、p2;(2) 子代解的第一种车辆向其中一个父代解学习,另一种车辆向另一种父代解学习.图5为交叉的具体步骤,给出了两个父代解,然后从p1取常温车辆,从p2取出冷藏车辆,从而得到相邻解.在本文中,交叉算子不需要进行任何修复过程就可以生成一个可行解. 在该算法中,这两种交叉算子都是随机选择的,然后当前的人工鱼以概率Pc向“可视范围”内的鱼群中心(最佳点)移动,或以1-Pc概率随机向邻近解移动.改进后的追尾行为可以在一定概率范围内学习最优解,从而具有跳出局部最优解的能力. 第二种交叉算法框架:Step 1:选择当前解xi的普通车辆部分,选择“可视范围”内最优解xbest的冷链车部分,将两部分组合起来;Step 2:如果xi的冷链车数量大于xbest的冷藏车数量,则全部复制,删去多余车辆;Step 3:选择当前解xi的冷藏车辆,选择“可视范围”内最优解xbest的常温车部分,将两部分组合起来;Step 4:如果xbest的冷藏车数量大于xi的冷链车数量,则全部复制,删去多余车辆;Step 5:原有目标值与重组后目标值进行比较,将最好解更新至公告板. 综上,改进的追尾行为算法框架.Step 1:循环初始解集的每一个解xi,根据“可视范围”确定解的邻域解集;Step 2:如果“可视范围”内存在最优解xbest,当xi周围不是很拥挤,且xbest的目标值比xi优秀,则xi向xbest移动,即xi与xbest进行交叉操作;Step 3:在公告板更新最好解;Step 4:如果移动不成功,则执行觅食行为. 改进的人工鱼群算法框架.Step 1:设置系统参数;Step 2:使用初始解生成策略初始化一个解决方案,对每个可行解进行评估;Step 3:采用车辆等待策略以提高客户满意度;Step 4:不满足停止条件时,执行下一步;Step 5:对于当前种群中的每个解进行局部搜索:Step 5.1:执行改进的觅食行为;Step 5.2:如果新生成的解决方案比前一个好,则替换成当前找到的最佳解决方案.Step 6:对于种群中的每个解,执行以下全局搜索:Step 6.1:执行改进的追尾行为;Step 6.2:如果新生成的解决方案比前一个更好,则替换到目前为止找到的最佳解决方案. SOLOMON算例是一种经典的VRPTW算例,它由56个算例组成,每个算例中又包含了100个客户点的详细信息.其中,算例中客户点的布局分为三类,分别是:具有高聚集度的Clustering系列17个,简称C系列算例;具有分散聚集度的Random系列算例23个,简称R系列算例;以及,中等聚集度的RC系列算例16个.表1给出了算例说明. 表1 算例说明 图6显示了 SOLOMON经典算例C101与R101的客户点分布图的特点.在多车型的冷链物流中,需要将冷藏货物与常温货物进行区别,这是与SOLOMON经典算例的一个很大的区别.因此,本文在SOLOMON经典算例的基础之上改进了客户的需求,增加了货物需求标志,其中需求普通货物的客户设置标志0,需求冷藏货物的客户设置标志1.同时,在扩展的经典SOLOMON算例中,将普通客户与冷藏客户的数量采用1:1到1:5之间随机生成的方法.扩展的55个SOLOMON算例将重新命名为“cc101”到“crc207”.但cc系列、cr系列和rcr系列这三类算例的主要特点与原有算例的特点保持一致,没有发生改变. 经典SOLOMON算例与扩展算例的主要区别如下:(1) 所有车辆分为两类:常温车辆和冷藏车辆;(2) 所有的客户也分为两类:只需要常温车辆运输常温产品的普通客户和需要用冷藏车辆运输冷冻货物的特殊客户;(3) 两类车型的容量和能耗能不同. 表2 车辆数据示例 在本实验中,主要参数有三个,包括Ra:邻域的半径,即人工鱼的“可视范围”visual.如果Ra=0.2,则表示一条人工鱼的“可视范围”是整个鱼群大小的20%.Ra越大,所涉及的邻域越大,当Ra=1时表示整个种群属于单个邻域范围.(2)Cr:拥挤参数;(3)Pc:跟随概率.根据详细的实验和已发表文献的参数对各个参数进行赋值,各参数的参数级别均设置为{0.2,0.4,0.6,0.9}.表3给出了参数水平表. 采用实验设计DOE Taguchi方法构造了一套正交阵列L16对参数进行组合,对于每个参数组合,使用IAFS算法独立运行30次并收集算法获得的平均适应度值作为响应变量(Response Variable,RV).图7给出了因子水平和交点.经过计算,IAFS算法表现最优的参数组合为Ra=0.2、Cr=0.6、Pc=0.2.同时,设置目标权重α=0.2. 表3 参数水平表 为了检验IAFS算法的性能,本文选择了三种经典的比较算法:混合进化算法(Hybrid Evolutionary Algorithm,HEA)[12]、禁忌搜索算法(Tabu Search,TS)[13]和自适应大邻域搜索启发式算法(Adaptive Large Neighborhood Search Heuristic, ALNS)[14].选择这三个算法作为比较算法的主要原因是针对异构车队约束条件下的VRPTW问题,HEA、TS以及ALNS是求解VRPTW问题常用算法.由于本文考虑的HVRPTW问题是VRPTW问题的一个扩展版本,只需这三种比较算法进行简单地扩展即可解决所考虑的问题.因此,在本研究中,将HEA、ALNS和TS算法在文献中提出的主要组件进行了重新编码,并对其进行了修改,以适应于求解HVRPTW问题.为了进行更公平的对比,对所有比较的算法进行了重新编码,并对其文献中的主要成分和参数进行了调整.此外,为了获得一个公允的结果,在相同的设备下,将四种比较算法进行了30次独立运行,并收集每个算例的最优值进行详细地比较. 表4显示了四种算法的比较结果,其中第三列到第六列分别为HEA、TS、ALNS算法和IAFS算法这四种比较算法对应每个算例的结果,并将同一算例中的最优值记录在表中的第二列.最后四列显示了这四种比较算法的结果与最优值之间的dev偏差.由表4中数据显示:在给定的55个算例中,所提出的IAFS算法获得了41个最优值,找到最优值的数量占总算例的74.5%,而排名第二的TS算法只得到8个最优值;表中最后一行为各个算法的平均性能,其中IAFS算法的dev偏差仅为1.55,而次优算法TS的dev偏差却为12.59;同时,与最近发表ALNS算法比较,可以从数据中得到ALNS算法的dev偏差为16.02,约为IAFS算法的10倍,充分证明了IAFS算法的求解能力.最后,将这四种算法进行多重比较,并通过方差分析得到了ANOVA分析图(图8),进一步验证了IAFS求解问题的性能明显优于其他三种算法. 此外,为了证明IAFS算法的收敛能力,进行详细的对比实验.针对ALNS与IAFS算法,选取crc103算例,对解决方案进行数据收敛实验,图9显示出两种算法的收敛性能.通过比较可以直观地看出,IAFS算法对求解HVRPTW问题具突出的收敛能力. 在图10的甘特图中,显示了算例“cc101”的求解结果,其中两种不同的颜色矩形代表了两种需要不同车型进行服务的客户点,客户点下面的数字是车辆完成该客户点服务的时间.例如,最上面一行中的客户点81则是使用冷藏车.因此,图10可证明IAFS算法对求解“cc101”算例是可行的. 表4 IAFS算法与其他算法的对比结果 续表4 IAFS算法与其他算法的对比结果 针对冷链物流中VRPTW问题,采用改进人工鱼群算法进行求解.分析了该算法的主要四个行为,并对算法进行了改进用于求解所提出的多车型冷链车辆路径问题.在IAFS算法中,首先设计了一种特殊的编码方法来考虑不同类型车辆的问题特征,接着通过改进的觅食行为和改进的追尾行为使算法更适用于求解离散优化问题.同时,通过改进的追尾行为在一定的概率范围内学习最优解,具备了跳出局部最优解的能力.为了验证改进后算法的性能,采用扩展的SOLOMON算例进行了验证,选择了三种经典的算法与IAFS算法进行了充分的对比实验,丰富的实验证明了所提出的IAFS算法对于求解多车型的冷链车辆路径问题具有良好的性能.未来的研究工作主要集中于进一步提升算法全局搜索和局部搜索能力方面.2 人工鱼群算法
2.1 初始解的产生
2.2 觅食行为
2.3 聚群行为
2.4 追尾行为
2.5 随机行为
3 改进人工鱼群算法设计
3.1 问题编码
3.2 问题解码
3.3 改进的觅食行为
3.4 改进的追尾行为
3.5 算法框架
4 试验分析
4.1 算例描述


4.2 实验参数
4.3 与其他算法的比较
5 结论

