利用奇异谱分析探测GPS 坐标时间序列时变周期信号
刘磊
(安徽省基础测绘信息中心 安徽合肥 230031)
1 引言
GPS 基准站坐标时间序列广泛应用于参考框架的建立与维持、地壳形变监测等高精度大地测量和地球动力学研究领域。几乎所有的GPS 基准站都呈现出显著的非线性运动变化(尤其是高程方向的周年、半周年特征)。随着地学等研究领域对大地测量成果所要求的精度越来越高,GPS 坐标时间序列中的非线性变化越来越受到关注[1]。
针对坐标时间序列非线性运动分析,众多学者利用最小二乘拟合(Least Squares Fitting, LSF)方法研究了基准站的非线性运动特征。然而,基于LSF 获取的基准站周期振幅和相位信息反映的是恒定的周期特征,无法顾及季节性信号的年际变化特征。为此,有关学者提出了利用卡尔曼滤波、小波分析等方法探测GPS 坐标时间序列中的年际非线性信号,取得了一定的成果。
奇异谱分析(Singular Spectrum Analysis, SSA)是用于研究非线性时间序列的有效方法,在大地测量学、气象学,海洋学等领域有着广泛的应用,可以直接从短而有噪声的时间序列中提取有效信息,不会被正弦波假定约束,更适合于时变周期的提取[2]。针对利用SSA 探测GPS 序列中的非线性信号,国内外学者也进行了一定的研究。王解先等利用SSA 对BJSH 站坐标时间序列缺失的数据进行插值,并分析了序列中的趋势项和周期项[3]。Chen 等利用SSA 提取GPS 坐标时间序列中的周期信号,通过多种方法的比较分析,验证了SSA 在提取时变季节信号中的价值[4]。周茂盛等提出了利用多通道奇异谱分析(MSSA)提取共模误差的新思路,该方法提高了坐标时间序列的精度[5]。
本文详细阐述了SSA 方法的基本原理,结合GPS 时间序列分析的实际,分析了SSA 中的周期信号分组与重构方法。进而以BJSH 站为例,将其应用于GPS 基准站坐标时间序列的分析,并与最小二乘拟合结果比较,探讨基准站的三维坐标周期变化特征。
2 原理与方法
2.1 奇异谱分析
奇异谱分析是对维度为N 的GPS 坐标时间序列C=(C1,C2,C3…CN) 进行分析并转化成多维坐标时间序列,从而将原始GPS 坐标时间序列进行分解并提取其中可靠信息。SSA 具体步骤主要分为四个部分:
1)嵌入
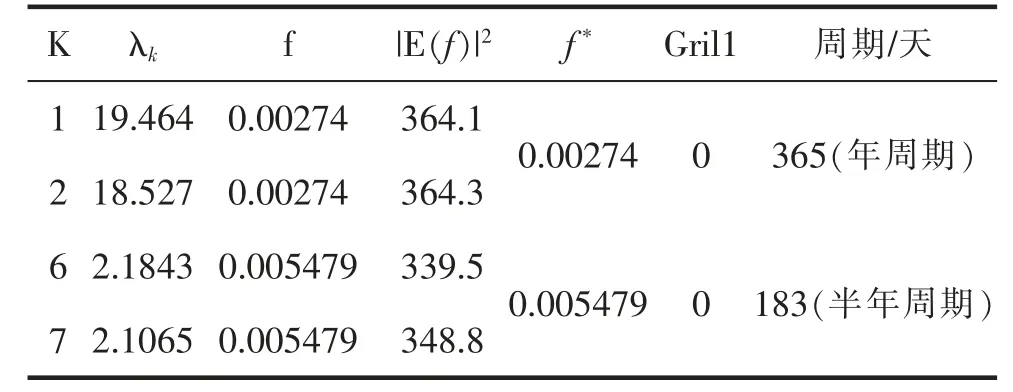
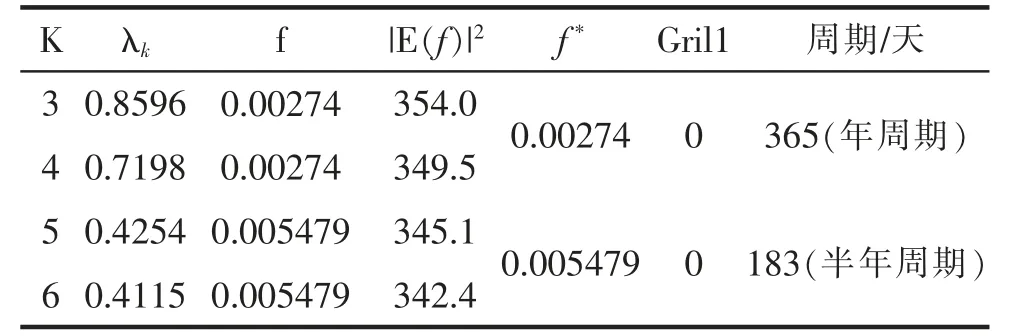
首先,将原始GPS 坐标时间序列C 转化成L×K的轨迹矩阵,其中L 为窗口长度,K=N-L+1(1 其中Cij=Ci+j-1 即反对角线上的元素都相等。 2)奇异值分解 3)特征三要素分组 将矩阵下标{1,2,3…d}分成m 个子集I1,I2,…Im,设I={i1,i2,…ip},得到合成矩阵CI=Ci1+Ci2+…+Cip。计算集合I=I1,I2,…,Im的每个合成矩阵,则分解后的序列为[6]: 4)重构GPS 坐标时间序列 将分组得到的矩阵转换成长度为N 的新序列,令X 为L×K 的矩阵,其中K=N-L+1,设L*=min{L,K},K*=max{L,K},根据对角平均化公式将矩阵X 转化为X1,X2…XN的时间序列,Xi,j为矩阵中的各元素(1≤i≤L,1≤j≤K)。对角平均公式为: 当原始GPS 坐标时间序列C1,C2,C3…CN中存在一个周期信号时,可以得到一对近似相等的特征值[6]。令这对特征值在序列中的位置为k 和k+1,那么满足所述条件的第k 个和第k+1 个RC(重构成分)之和构成了原始GPS 坐标时间序列的一个周期信号。 由于时间序列往往是离散的,根据上述条件确定周期信号具有一定缺陷。因此,根据Vautard 等的研究,补充三个准则来识别周期信号[7]: (1) 两个连续特征值近似相等,且在序列中足够大; (2) 对应的两个T-EOF 必须频率相近,对TEOFk和T-EOFk+1傅里叶变换后得到Ek(f)和Ek+1(f),找出达到最大值的|Ek(f)|2和|Ek+1(f)|2所对应的频率fk和fk+1,其中,两频率的差值δfk=|fk+1-fk|应很小。 (3) |Ek(f)|2和|Ek+1(f)|2足够大,也就是说介于fk和fk+1之间的一个频率f*可以通过这一对特征成分反映出来。 说明原始序列的中间频率f^*的周期性变化至少有2/3 可通过这对特征成分所表示。 GPS 基准站坐标时间序列可以表示为: 式中,ti是以一年为单位的观测值i 的时间,Y0是一个恒定的初始偏移量,v 是一个恒定的速度,ak和bk是周期项的系数,fk是周期频率,(ti) 是噪音的含量。如果将线性趋势与年周期(f1=1 cpy)和半年周期(f2=2 cpy)信号一起分解,那么矩阵A 变为: 未知向量x 是 最小二乘的主要优点是易于实现,并能直观地解释线性趋势和季节振幅的估计,但是最小二乘只能获得恒定的振幅或相位,其缺点在于长周期的变化可能被误认为是一种线性趋势。 本文选择陆态网提供的基准站坐标时间序列(以BJSH 站为例),利用SSA 对其进行周期性运动分析。考虑到本文研究的是时间序列的周期变化特征,选择去趋势的BJSH 站结果进行分析。此外,由于数据存在缺失,本文采用三次多项式插值得到BJSH 站2000 年-2017 年连续的单天坐标时间序列。 应用SSA 分析GPS 坐标时间序列时,窗口长度L 的选择对于获取正确的结果至关重要。L 越大,原始序列的分解越精细,但过大的L 不利于奇异值分解的运算;如果 L 太小,则奇异值分解将导致不同的成分相互混杂,不利于信号的提取。Vautard 等研究发现[8],SSA 能够分解出周期介于L/5 和L 之间的信号。Ghil 等提出,在选择窗口滞后时间时,应兼顾两个因素[9]:所提取的信息量与对该信息的统计置信度。前者要求窗口滞后应尽可能宽,即一个较大的L,而后者则要求尽可能多地重复感兴趣的特征,即尽可能大的N/L 比。文献[3]通过模拟实验也证明了从GPS 坐标时间序列中提取年度和半年周期时,选择2 年或3 年的滞后窗口是合适的。因此,本文在利用SSA 研究GPS 坐标时间序列的年变化和半年变化时,选择两年的窗口长度将GPS 时间序列分解成730 种时间模式,进而获取其年周期和半年周期信号特征。 3.2.1 SSA 分析结果 图1(左)为BJSH 站高程方向经SSA 分析时数据方差各部分的归一化特征值按降序排列结果。由图可知,前两个最大的特征值分别可以解释数据方差的34.21%和6.13%。图1(右)显示了前50 个相应的特征值EOFs 对应的主周期频率,从图中可以清楚地看出年周期的特征值和半年周期的特征值。取前两对数值相近的特征值,将其对应的重构分量分为两对,如图2 图3 显示了特征值对应的两对经验正交函数(EOFs)和相应的重构分量(RCs),分别代表年周期信号和半年周期信号。图4 描述了原始GPS基准站高程时间序列、利用SSA 提取的年周期和半年周期。由图可知,BJSH 站的周期振幅随时间变化而不同,具有显著的时变特征,而SSA 能够有效地提取GPS 坐标时间序列中的时变周期。 图1 (左)GPS 高程数据协方差矩阵得到的归一化特征值;(右)特征值EOFs 对应的主周期频率 图2 特征值对应的两对EOFs 年周期和半年周期 图3 特征值对应的两对RCS 年周期和半年周期 图4 GPS 高程坐标时间序列、重建年信号、重建半年信号 3.2.2 测站N,E,U 三个方向上的周期项探测 根据2.2,当存在一对近似相等的特征值时,符合补充准则的一对特征成分的两个RC 之和表示原始坐标时间序列中的一个周期项。表1~表3 分别给出了U、N、E 三个方向上主要成对RC 的周期项分析结果,其中K 为选择的重构分量,λk为对应的特征值,f 为|E(f)|2最大值对应的频率,|E(f)|2为TEOFk经过傅里叶变换后的值,f*为一对特征值对应的频率的均值。 表1 U 方向上主要成对RC 的周期项分析 根据表中的三对RC 的分析结果,发现U 方向上前两个特征值较大的重构分量RC 对应年周期,第二对RC 对应半年周期,而其余的RC 则不能满足上述的检验标准,无法探测出周期项信号。 采用同样的方法对BJSH 站N、E 分量的时间序列分别进行周期项探测(表2、表3)。结果表明N 方向上无法探测出1/3 年周期,而且不同方向上选取的RC 也不同,但前几个较大的特征值对应的重构分量都对应着年周期、半年周期。 表2 N 方向上主要成对RC 的周期项分析 表3 E 方向上主要成对RC 的周期项分析 综合BJSH 站三个方向上的周期项探测,可以得出以下结论:BJSH 站在不同方向都近似存在年周期、半年周期项,但不同方向上存在的周期项也有略微不同,比如1/3 年周期等。 本文进一步分析了SSA 与LSF 提取GPS 坐标时间序列周期特征的差异,如图5 所示。 图5 U 方向上LSF 和SSA 对比图,(a)SSA 与LSF 年周期对比图;(b)SSA 与LSF 半年周期对比图;(c)SSA 与LSF 主周期对比图 (1)SSA 得到的年周期与LSF 得到的年周期作对比,如图5(a)所示。从图中可以看出,SSA 与LSF都具有提取周期项的能力。并且可以清楚地观察到,2006-2011 年间SSA 拟合的波峰比LSF 拟合的结果更接近原始序列的波峰,2012-2016 年间SSA 拟合的波谷比LSF 拟合的结果更接近原始序列的波谷。 (2)SSA 得到的半年周期与LSF 作对比,如图5(b)所示。图5(b)比图5(a)的区别要更明显,随着时间的推移,SSA 与LSF 得到的峰值产生明显的偏移。 (3)比较SSA 得到的主周期信号(年周期加半年周期)与最小二乘拟合得到的主周期信号(年周期加半年周期),如图5(c)所示。从图中可以看出,在最小二乘拟合中,季节性信号在每年的5 月中旬达到峰值;在SSA 中,获得的季节性信号随时间而变化。 综合SSA 与LSF 比较的结果发现,SSA 得到的周期信号能随原始坐标时间序列的变化而变化,而最小二乘拟合的结果只能得到振幅和相位恒定的周期信号,因此SSA 在提取GPS 坐标时间序列非线性信号上有明显的优势。 本文详细研究了SSA 方法应用于GPS 坐标时间序列分析的基本原理,通过SSA 对BJSH 站GPS坐标时间序列的处理和分析,研究了GPS 基准站的周期项特征。与LSF 结果比较发现,SSA 提取的周期项与原始信号的周期项吻合程度优于LSF 估计的结果,尤其是对于年际变化特征而言,SSA 显著优于LSF。根据本文SSA 对BJSH 站的周期项探测发现,BJSH 站在U、N、E 三个方向上存在显著的周期变化特征,但各方向上探测的周期项存在差异。BJSH 站的周期项并不是严格的年周期、半年周期。本文没有深入分析影响周期项的主要因素,如何根据影响周期项的因素给出解决问题的办法有待进一步研究。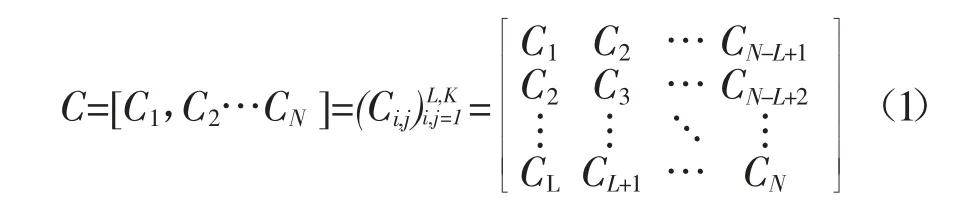



2.2 基于SSA 的周期信号分离方法
2.3 最小二乘拟合



3 结果与分析
3.1 SSA 窗口长度L 的选择
3.2 周期项探测





3.3 SSA 与LSF 比较分析

4 结束语

