发展不平衡视角下地方监管沙盒竞争的演化博弈分析
张红伟,陈小辉,文 佳,吴永超
(1.四川大学经济学院,四川 成都 610064;2.中国人民银行海口中心支行,海南 海口 570105;3.四川大学研究生院,四川 成都 610064)
1 引言
在新一轮科技革命和产业变革的背景下,金融科技(FinTech)成为金融与科技深度融合创新的产物[1],与科技金融是概念截然不同的两个概念[2]。Arner等[3]进一步指出,2008年以来全球FinTech已进入3.0时代。FinTech使金融体系面临着一种DNA式的变化,FinTech为代表的金融创新是中国金融崛起的新路径[4]。另一方面,徐忠等[5]在分析FinTech的风险特性后指出,FinTech还存在监管套利与法律风险,在宏观层面,一旦风险暴露可能在短时间内迅速演变为大规模的系统性金融风险。柴瑞娟[6]研究指出,FinTech使科技安全风险和传统金融风险叠加。罗福周等[7]也从机构层面、系统层面剖析了金融科技为金融业发展带来的风险。
实际上,美国、英国和日本等发达国家也同样面临FinTech给其金融体系带来的积极意义和挑战问题。怎么办?2015年3月,英国政府率先提出监管沙盒概念,同年11月英国金融行为局发布监管沙盒白皮书,开始实行监管沙盒,力求促进金融科技发展。新加坡、澳大利亚、泰国、韩国、中国香港和台湾地区纷纷效仿,相继推出监管沙盒。
在相关国家和地区纷纷实践监管沙盒的同时,国内外学者围绕监管沙盒的概念、积极作用、局限性和中国实施监管沙盒的必要性等进行了较为广泛的研究。
关于监管沙盒的概念。Castri和Plaitakis[8]认为,监管沙盒是一个受控环境,在该环境中金融创新者可在一定期限内测试其方案而不必立即承担常规监管成本,且其金融产品也无需满足现行法律要求。Bromberg等[9]认为,监管沙盒是一个“安全”环境,在这“安全”环境中企业可测试FinTech创新产品,监管机构可视具体案例放松监管规则。蔡瑞娟[6]认为,监管沙盒是一种新的监管工具,旨在为具有破坏性和众多风险的金融创新提供安全的测试环境和监管实验区。尹海员[10]认为,监管沙盒主要是以实验的方式,创造一个“安全区域”,适当放松参与实验的创新产品和服务的约束,激发创新活力。四个概念均强调监管沙盒可放松监管、促进创新的本质特性。
关于监管沙盒的积极作用。Arner等[11]认为,监管机构在“监管沙盒”中的积极态度,有助于促使监管模式发生转变。监管机构借助“监管沙盒”建立监管新框架,可提振市场信心[12]。Bromberg等[9]指出,一个良好的监管沙盒应该在测试阶段以一种良好的方式保护消费者权益,同时达到缓和金融风险和稳定金融市场的作用。Fan[13]认为,监管沙盒能很好地平衡鼓励金融创新、保护金融消费者和维护金融稳定三者之间的关系。Chang-Hsien和Peng[14]指出,监管沙盒以一种“轻触”式监管促进金融创新,同时保护金融消费者权益和防范潜在系统性金融风险。Lee[15]认为,监管沙盒作为一种放松监管的工具,可用于鼓励金融创新据此发展金融中心。申嫦娥和魏荣桓[16]提出我国要采取友好型监管方式寻找FinTech发展与监管之间的平衡点。徐忠等[5]认为,监管沙盒可为企业提供完善产品和服务的可靠依据,防范潜在金融风险。张景智[17]认为,监管沙盒是现行法律框架下的相机决策制度安排,具有甄别、宣示和窗口作用。这些学者对监管沙盒的作用进行了准确界定。Lee[15]的研究结论表明监管沙盒除作为监管工具外,还是一种“招商引资”工具,中国地方政府推出监管沙盒,“招商引资”也是其主要目的之一。
关于监管沙盒的局限性。Zetzsche等[18]认为监管沙盒高度依赖于现行的监管体制,具有一定的局限性。赵杰等[19]认为,其可能产生新的不公平竞争。
关于中国实施沙盒监管的必要性。徐忠等[5]、蔡瑞娟[6]、张红伟和陈小辉[20]均倾向于,中国有必要借鉴国外经验,结合中国实际情况,建设中国监管沙盒,对金融科技实施沙盒监管;徐忠等[5]更进一步,将监管沙盒置于包容性监管体系之内。这些研究成果,在一定程度上解决了中国监管沙盒的必要性问题。
黄震和蒋松成[21]指出,中国和英国已于2017年就金融科技监管沙盒达成了合作协议。截止目前,中国北京市房山区、贵州省贵阳市、江西省赣州市等地方也推出了监管沙盒。那么,在中国幅员辽阔且发展不平衡的背景下,若各地方纷纷推出监管沙盒,其最终结局如何呢?本文基于地方政府的有限理性,采用演化博弈模型,讨论前述问题。
本文的创新点和贡献主要体现在以下三个方面:一是基于中国发展不平衡的基本国情,利用演化博弈模型,率先研究中国各地方监管沙盒竞争的最终结局问题。二是基于支付函数,根据演化博弈分析结果,首次进行了增益分析并据此得出相关命题和推论。三是在相关命题和推论基础上,首次有针对性地提出了对地方监管沙盒进行中央层面管理的相关政策建议。
2 研究假设
为促进本地金融、经济发展,地方政府可基于监管沙盒的放松管制和促进FinTech创新等功能实行招商引资。但与其他制度安排不同,监管沙盒在放松管制、促进FinTech创新的同时,会衍生金融风险,并且还可能向异地外溢。另一方面,基于发展不平衡的基本国情,经济发达地区符合FinTech创新相关风险控制标准的企业和个人(简称“潜在适格客户”)较多,同等条件下FinTech从业机构收入较多,地方政府的收入也较多(这里的地方政府收入指除财政收入等直接收入外,还包括FinTech从业机构解决当地就业问题产生的间接收入);反之,经济欠发达地区,潜在适格客户相对较少,同等条件下FinTech创新给地方政府带来的收入较少。由于FinTech创新始终伴随着风险,一旦风险发生导致风险事件,将可能给地方政府带来风险损失成本,此外地方政府推行监管沙盒还将产生固定成本。
地方政府推出监管沙盒后,入驻沙盒内的FinTech从业机构数量记为x,x个FinTech从业机构实施的FinTech创新数量记为y,潜在适格客户数量记为z,FinTech创新的业务量记为w,则地方政府的收入函数f=f(x,y,z,w)。监管沙盒的风险发现能力记为d,监管沙盒内FinTech从业机构的平均风险管理水平记为l,则监管沙盒内的风险数量r=g(y,w,d,l),风险带来的损失成本v=v(r),监管沙盒产生的固定成本记为F。则地方政府实施监管沙盒的净收益
NR=f(x,y,z,w)-v(g(y,w,d,l))-F
(1)
为简化分析,本文作如下假设。
假设1:边际收入递减假设。因给地方政府带来高收入的FinTech从业机构数量相对有限,随着入驻监管沙盒内的FinTech从业机构数量x增加,地方政府的收入增加,但边际收入递减。由于潜在适格客户及其有效需求有限,地方政府的收入随着FinTech创新数量y和业务量w的增加而增加,但边际收入递减。因高净值适格客户有限,故随着潜在客户数量的增加,地方政府的收入会增加,但边际收入递减。f(x,y,z,w)的完整假设为在[0,∞)上连续,在(0,∞)内可导,并且具有如下性质:
fx(x,y,z,w)>0,fxx(x,y,z,w)<0;
fy(x,y,z,w)>0,fyy(x,y,z,w)<0;
fz(x,y,z,w)>0,fzz(x,y,z,w)<0;
fw(x,y,z,w)>0,fww(x,y,z,w)<0。
k=x,y,z,w
(2)
假设2:边际风险递增假设。因风险的外溢性,风险数量r随着FinTech创新数量y的增加而增加,且增速递增。因优质客户(如信用良好的客户)数量及其需求相对有限,风险数量r随着业务量w的增加而增加,且增速递增。因越隐蔽风险越难发现和管理,风险数量r随着监管沙盒风险发现能力d和监管沙盒内FinTech从业机构平均风险管理水平l的增加而减少,但减速递减。g(y,w,d,l)的完整假设为在[0,∞)上连续,在(0,∞)内可导,并且具有如下性质:
gy(y,w,d,l)>0,gyy(y,w,d,l)>0;
gw(y,w,d,l)>0,gww(y,w,d,l)>0;
gd(y,w,d,l)<0,gdd(y,w,d,l)<0;
gl(y,w,d,l)<0,gll(y,w,d,l)<0。
k=y,w
(3)
假设3:边际损失成本递增假设。由于风险的传染性,风险带来的损失成本v随着风险数量r的增加而增加,且增速递增。v(r)的完整假设为在[0,∞)上连续,在(0,∞)内可导,并且具有如下性质:
v′(r)>0,v″(r)>0,v(0)=0。
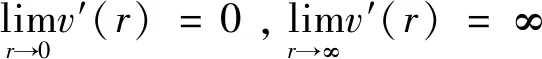
(4)
假设4:净收益地区差异假设。中国幅员辽阔,但发展不平衡,发达地区和欠发达地区经济金融发展差距较明显。FinTech从业机构比较青睐发达地区地方政府的监管沙盒,且入驻发达地区地方政府监管沙盒的FinTech从业机构整体实力较强,发达地区的金融、经济实力和人才也更具优势。故,假设发达地区地方政府单独实施监管沙盒时,其净收益为正,发达地区地方政府与欠发达地区地方政府同时实施监管沙盒时,发达地区的净收益可正、可负、也可为零,而欠发达地区地方政府不管单独实施还是和发达地区地方政府同时实施,其净收益均可正、可负,也可为零。
3 模型设定
3.1 模型总述
(1)博弈方
根据假设4,中国34个省级、334个地市级和2876个县级行政单位可划分为发达地区和欠发达地区,演化博弈在发达地区地方政府群体和欠发达地区地方政府群体之间进行。故,博弈方分别为发达地区地方政府即Developed博弈方,欠发达地区地方政府即Developing博弈方。
(2)博弈方策略
Developed与Developing博弈方均存在“推出监管沙盒,实放松管制和促进FinTech创新”策略和“不推出监管沙盒”策略。故, Developed和Developing博弈方的博弈策略均为(实施、不实施)。
(3)演化博弈稳定点
设Developed和Developing群体中选择“实施”策略的比例分别为p、q。在qp平面内,按Friedman[22]均衡算法,Developed和Developing博弈方动态博弈的均衡点为E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)、E5(p**,q**)。当演化博弈结果收敛于稳定点E2(0,1)时,q=0、p=1,即欠发达地区地方政府均选择“不实施”策略,而发达地区地方政府100%选择“实施”策略。其他稳定点类推。
(4)博弈方目标
博弈方的目标为最大化其净收益,博弈双方的净收益函数(即博弈方的支付)均为公式(1)、具体变量有别且均受假设1—4约束。具体变量如下:
Developed和Developing博弈方监管沙盒内的FinTech从业机构数量分别记为Ae、Ai。Developed和Developing博弈方监管沙盒内的FinTech创新数量分别记为Ie、Ii。设Developed和Developing博弈方所在地的潜在适格客户数量分别为Ce、Ci,FinTech创新吸纳本地潜在适格客户的比例为α。
发达地区经济金融发达,潜在适格客户较多。因此,设为:
Ce>Ci
(5)
由于FinTech创新具有跨地域服务能力,监管沙盒内的FinTech创新出吸引本地潜在适格客户外,还会吸引异地潜在适格客户。设Developed和Developing博弈方监管沙盒内的FinTech创新吸引Developing和Developed博弈方所在地的潜在适格客户的比例分别为βe、βi,则Developed和Developing博弈方监管沙盒内的FinTech创新吸引的Developing和Developed博弈方所在地的客户数量分别为βeCi和βiCe。Developed和Developing博弈方监管沙盒内FinTech创新的业务量分别记为We、Wi。
FinTech创新在吸引异地适格客户的同时,也会向异地外溢风险。设风险外溢因子为γ,则Developed博弈方监管沙盒内FinTech创新产生的风险数量为r时,向Developing博弈方外溢风险的数量为γr。Developing博弈方向Developed博弈方外溢的风险数量也为γr。Developed和Developing博弈方监管沙盒的风险发现能力分别记为de、di。Developed和Developing博弈方监管沙盒内的FinTech从业机构的平均风险管理水平分别记为le、li。设发达地区和欠发达地区监管沙盒的固定成本分别为Fe、Fi。
(5)博弈双方的支付矩阵
博弈双方的支付矩阵如表1所示。其中,Developed和Developing博弈方均选择“实施”策略时,Developed博弈方的支付(payoffs)记为F11,Developing博弈方的支付记为R11。其它情形类推。

表1 Developed博弈方与Developing博弈方的支付矩阵
博弈双方的支付因双方策略选择不同而异,具体如下。
3.2 支付函数
(1)F11和R11
Developed和Developing博弈方均选择“实施”策略时,Developed博弈方监管沙盒内的FinTech创新的适格客户总数为αCe+βeCi,Developing博弈方监管沙盒内的FinTech创新吸引的适格客户总数为αCi+βiCe。
Developed和Developing博弈方监管沙盒内FinTech创新产生的风险数量分别为g(Ie,We,de,le)、g(Ii,Wi,di,li)。
则Developed博弈方承受的风险总数量为:
g(Ie,We,de,le)+γg(Ii,Wi,di,li)
(6)
Developing博弈方承受的风险总数量为:
γg(Ie,We,de,le)+g(Ii,Wi,di,li)
(7)
因此,
F11=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-Fe
(8)
R11=f(Ai,Ii,αCi+βiCe,Wi)-v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-Fi
(9)
(2)F12和R12
Developed博弈方选择“实施”策略,Developing博弈方选择“不实施”策略时,Developed博弈方监管沙盒内的FinTech创新的适格客户总数为αCe+βeCi,其承受的风险总数量为g(Ie,We,de,le)。Developing博弈方承受的风险总数量为γg(Ie,We,de,le)。因此,
F12=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le))-Fe
(10)
R12=-v(γg(Ie,We,de,le))
(11)
由假设4知:
F12>0
(12)
(3)F21和R21
Developed博弈方选择“不实施”策略,Developing博弈方选择“实施”策略时,Developing博弈方监管沙盒内的FinTech创新的适格客户总数为αCi+βiCe,其承受的风险总数量为g(Ii,Wi,di,li)。Developed博弈方承受的风险总数量为γg(Ii,Wi,di,li)。因此,
F21=-v(γg(Ii,Wi,di,li))
(13)
R21=f(Ai,Ii,αCi+βiCe,Wi)-v(g(Ii,Wi,di,li))-Fi
(14)
4 演化分析
4.1 复制动态方程与雅克比矩阵

uec=qF11+(1-q)F12
(15)
ueu=qF21
(16)
(17)

uic=pR11+(1-p)R21
(18)
uiu=pR12
(19)
(20)
则Developed群体选择“实施”策略的比例的复制动态方程为:
(21)
Developing群体选择“实施”策略的比例的复制动态方程为:
(22)
为简化讨论,令A=F11-F21,B=F12,D=R11-R12,E=R21。
由(8)式和(13)式,得:
A=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-Fe+v(γg(Ii,Wi,di,li))
(23)
由(9)式和(11)式,得:
D=f(Ai,Ii,αCi+βiCe,Wi)-v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-Fi+v(γg(Ie,We,de,le))
(24)
由(21)式和(22)式可得雅克比矩阵:
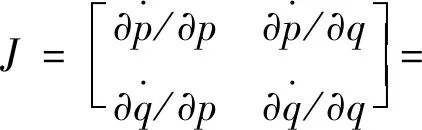

(25)
4.2 复制动态相位图
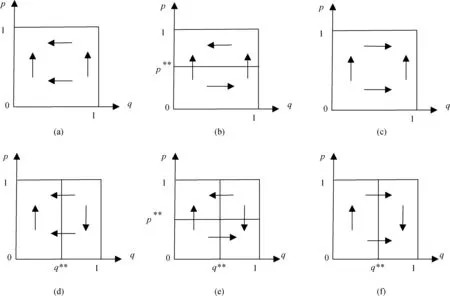
4.2.1 Developed博弈方
由(12)式知,B=F12>0。由(10)式和(23)式,得:
B-A=v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-v(γg(Ii,Wi,di,li))-v(g(Ie,We,de,le))
(26)
构造辅助函数可证明(证明过程可索取):
B-A≥0
(27)
尽管q**取值不在[0,1]上时无意义,但为进行动态关系分析,仍需进行讨论:当B=A时,q**=∞;当A=0时,q**=1;当A>0时,q**>1;当A<0时,0 (1)q**=∞ 当B=A时,q**=∞。由(21)式知,dp/dt>0,此时p*=1为ESS(图1a)。 (2)1 当A>0时,1 (3)q**=1 当A=0时,q**=1。由(21)式知,dp/dt>0,此时p*=1为ESS(图1c)。 图1 q**≥1时Developed博弈方复制动态相位图 (4)0 当A<0时,0 图2 0 4.2.2 Developing博弈方 由(14)式和(24)式,得: E-D=v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-v(γg(Ie,We,de,le))-v(g(Ii,Wi,di,li)) (28) 同理,可得: E-D≥0 (29) D和E的符号均不确定,但受(29)式约束。存在p**<0,p**=0,0 均衡点为E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)、E5(p**,q**)。将q**的四种情况合并为q**>1、q**=1和0 4.3.1q**>1 (1)p**<0。因p**、q**均无意义,因此E5(p**,q**)不在qp单位平面内。此时只有E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)四个均衡点。此时,(A=B∨A>0)∧(E<0∧D≤E),式中“∨”表示逻辑“或”运算,“∧”表示逻辑“与”运算。当(A=B)∧(E<0∧D≤E)时,由(12)和(25)式可得雅克比矩阵的行列式和迹的符号,由此判断均衡点的稳定性情况如表2。 表2 雅克比矩阵局部均衡分析 结合相位图,动态关系及稳定性如图3a。同理,当(A>0)∧(E<0∧D≤E)时,动态关系及稳定性如图3a。因此,当(A=B∨A>0)∧(E<0∧D≤E)时,E2(0,1)是稳定点。 其余十四种情形类推,动态关系及稳定点分析如下: (2)p**=0。(A=B∨A>0)∧(E=0∧D<0)时,E2(0,1)是稳定点,动态关系及稳定点如图3a。 (3)0 (4)p**=1。(A=B∨A>0)∧(E>0∧D=0)时,E4(1,1)是稳定点,动态关系及稳定性如图3c。 (5)p**>1。(A=B∨A>0)∧(E>0∧D>0∧E≥D)时,E4(1,1)是稳定点,动态关系及稳定性如图3c。 4.3.2q**=1 (1)p**<0。A=0∧E<0∧DSymbolcB@E,E2(0,1)是稳定点,动态关系及稳定点如图3a。 (2)p**=0。A=0∧E=0∧D<0,E2(0,1)是稳定点,动态关系及稳定点如图3a。 (3)0 (4)p**=1。A=0∧E>0∧D=0,E4(1,1)是稳定点,动态关系及稳定性如图3c。 (5)p**>1。A=0∧E>0∧D>0∧E≥D,E4(1,1)是稳定点,动态关系及稳定性如图3c。 4.3.3 0 (1)p**<0。A<0∧E<0∧D≤E,E2(0,1)是稳定点,动态关系及稳定点如图3d。 (2)p**=0。A<0∧E=0∧D<0,E2(0,1)是稳定点,动态关系及稳定点如图3d。 (3)0 (4)p**=1。A<0∧E>0∧D=0,E3(1,0)是稳定点,动态关系及稳定性如图3f。 (5)p**>1。A<0∧E>0∧D>0∧E≥D,E3(1,0)是稳定点,动态关系及稳定性如图3f。 图3 复制动态关系及稳定性 综上,Developed群体与Developing群体演化博弈的最终结果可分为四种情形:一个稳定点E2(0,1)、一个稳定点E3(1,0)、一个稳定点E4(1,1)、同时存在E2(0,1)和E3(1,0)两个稳定点,其具体条件如表3。 稳定点E2(0,1)E3(1,0)E4(1,1)E2(0,1)和E3(1,0)具体条件其他A<0∧E>0∧D≥01.(A=B∨A>0)∧(E>0∧D≥0)2.A=0∧E>0∧D≥0A<0∧E>0∧D<0 表3表明,稳定点的具体条件取决于A、D、B、E取值。影响四者取值的因素及方向如下: 5.1.1 Developed共生增益A A=F11-F21,也就是Developing博弈方选择“实施”策略时,Developed博弈方选择“实施”策略与选择“不实施”策略相比,Developed博弈方增加的支付。由于此时两博弈方均可能选择“实施”,故将该支付称为“Developed共生增益”。A的具体表达式见公式(23)。 (23)式中,Developed博弈方所在地的潜在适格客户数量Ce和Developing博弈方所在地的潜在适格客户数量Ci、Developed博弈方监管沙盒的固定成本Fe为外生变量,不受Developed博弈方控制。风险外溢因子γ,Developed博弈方也极难控制,本文将其视为不受Developed博弈方控制。Ii、Wi、di、li四个变量受Developing博弈方控制。因此,Developed博弈方可控制或影响的变量为Ae、Ie、α、βe、We、de、le。其中,Developed博弈方监管沙盒内的FinTech从业机构数量Ae,由其在实施监管沙盒时制定的相关准入政策以及后续招商力度控制;Developed博弈方监管沙盒内的FinTech创新数量Ie,Developed博弈方可通过监管沙盒内的制度约束放松程度、监管沙盒内人才吸引政策等予以控制;FinTech创新吸引本地潜在适格客户的比例α,Developed博弈方具有一定的影响力,在风险可控条件下,允许FinTech从业机构采用更多的宣传工具提高α,反之,也可降低α。Developed博弈方监管沙盒内的FinTech创新吸引Developing博弈方所在地的潜在适格客户的比例βe,Developed博弈方可通过控制跨地域经营的FinTech从业机构数量,影响βe。Developed博弈方监管沙盒内FinTech创新的业务量We,出于防范风险等需要,Developed博弈方可能通过规定最高业务量限额等措施施加影响之。Developed博弈方监管沙盒的风险发现能力de,Developed博弈方可通过改进监管沙盒的质量进行控制。Developed博弈方监管沙盒内的FinTech从业机构的平均风险管理水平le,Developed博弈方既可以通过监管沙盒的准入政策予以控制,也可采取后续风险提示、专业人员培训等方式进行控制。Ae、Ie、α、βe、We、de和le等变量的影响方向,具体如下: (1)Ae、α、βe 公式(23)对Ae求偏导,结合(2)式得:∂A/∂Ae=fAe>0。因此,监管沙盒内FinTech从业机构数量越多,Developed共生增益越大。同理,(23)式分别对α、βe求偏导,结合(2)式可得:∂A/∂α>0、∂A/∂βe>0,即A随着α、βe的增加而增加。 (2)创新数量Ie 公式(23)对Ie求一、二阶偏导,由(2)、(3)、(4)式知,存在唯一ξIe∈(0,∞),在其他条件不变情况下,当Ie∈(0,ξIe)时,A随着Ie增加而增加;当Ie∈(ξIe,∞)时,A随着Ie增加而减少。 (3)业务量We 公式(23)对We求一、二阶偏导,结合(2)和(3)式知,存在唯一ξWe∈(0,∞),在其他条件不变情况下,当We∈(0,ξWe)时,A随着We增加而增加,当We∈(ξWe,∞)时,A随着We增加而减少,当We=ξWe时,A取最大值。 (4)de和le 另一方面,受Developing博弈方控制的Ii、Wi、di、li四个变量,也会对Developed的共生增益产生影响。具体如下: (5)Ii和Wi 公式(23)对Ii求一阶偏导,得∂A/∂Ii=γgIi[v′(γg(Ii,Wi,di,li))-v′(g(Ie,We,de,le)+γg(Ii,Wi,di,li)],由(3)和(4)式知,∂A/∂Ii<0。同理,对Wi求一阶偏导,可得,∂A/∂Wi<0。即,Developed共生增益A随着Developing博弈方监管沙盒内的创新数量Ii和监管沙盒内创新的业务量Wi的增加而减少,且与自身沙盒内的创新数量Ie、和业务量We不同,Ii和Wi并不存在临界点,而是随着两者的增加而单调减少。 (6)di和li 公式(23)对di求一阶偏导,∂A/∂di=γgdi[v′(γg(Ii,Wi,di,li))-v′(g(Ie,We,de,le)+γg(Ii,Wi,di,li)],由(3)和(4)式知,∂A/∂di>0。同理,对li求一阶偏导,可得,∂A/∂li>0。与Ii和Wi相反,Developed共生增益A随着di和li的增加而单调增加。 综合对Developed共生增益A的分析,可得如下命题1。 命题1:Developed和Developing博弈方均可改变Developed共生增益A。但双方控制的变量和影响方向不同。Developed博弈方可控制的变量有Ae、Ie、α、βe、We、de、le,其中A随Ae、α、βe、de和le的增加单调增加,le和We存在临界点,临界点以下A随Ie和We的增加单调增加,临界点以上随Ie和We的增加单调减少,临界点处取最大值。Developing博弈方可控制的变量有Ie、We、de、le,其中A随Ii和Wi的增加单调减少,随di和li的增加单调增加。 5.1.2 Developing共生增益D D=R11-R12,Developed博弈方选择“实施”策略时,Developing博弈方选择“实施”策略与选择“不实施”策略相比,Developing博弈方增加的支付。同理,将该支付称为“Developing共生增益”。D的具体表达式见公式(24)。 由于(23)式和(24)式具有对称性,比照命题1,可得命题2。 命题2:Developed和Developing博弈方均可改变Developing共生增益D。但双方控制的变量和影响方向不同。Developing博弈方可控制的变量有Ai、Ii、α、βi、Wi、di和li,其中D随Ai、Ii、α、βi、di和li的增加单调增加,Ii和Wi存在临界点,临界点以下D随Ii和Wi的增加单调增加,临界点以上随Ii和Wi的增加单调减少,临界点处取最大值。Developed博弈方可控制的变量有Ie、We、de、le,其中D随Ie、We的增加单调减少,随de和le的增加单调增加。 由命题1和命题2,可得如下推论1、2、3。 推论1:Developed和Developing双方之间的博弈,竞争FinTech从业机构并非唯一路径,改进自身监管沙盒质量、提高监管沙盒风险发现能力,提供风险提示等服务、改善FinTech从业机构平均风险管理水平等也是可能路径,而且是更可控制的精细化路径。 推论2:监管沙盒风险发现能力和监管沙盒内FinTech从业机构平均风险管理水平的提高,具有正外部性;监管沙盒内FinTech创新数量和创新业务量具有负外部性。 推论3:在承担风险损失成本(即对监管沙盒内的风险承担责任)的情况下,出于提高共生增益A、D考虑,地方政府将会理性控制其建立的监管沙盒内的FinTech创新数量和创新的业务量,不会让其无限度增加。但若不承担风险损失成本,则其出于提高共生增益A、D考虑,将可能无限度增加其建立的监管沙盒内的FinTech创新数量和创新的业务量。 5.2.1 Developed独建增益B B=F12,即Developing博弈方选择“不实施”策略时,与选择“不实施”策略获得的支付相比,Developed博弈方增加的支付。由于此时仅Developed博弈方选择“实施”,故将该支付称为“Developed独建增益”。B的具体表达式见公式(10)。公式(10)中,Ae、Ie、α、βe、We、de和le为Developed博弈方可控制的变量,Ce、Ci和Fe为外生变量,但与共生增益A不同的是,Developing博弈方并不能影响B。对(10)式求偏导,可得命题3。 命题3:仅Developed博弈方可改变Developed独建增益B。Developed博弈方可控制的变量有Ae、Ie、α、βe、We、de和le,其中B随Ae、α、βe、de和le的增加单调增加,Ie和We存在临界点,临界点以下B随两者的增加单调增加,临界点以上随两者的增加单调减少,临界点处取最大值。 5.2.2 Developing独建增益E E=R21,即Developed博弈方选择“不实施”策略时,与选择“不实施”策略获得的支付相比,Developing博弈方增加的支付。同理,称为“Developing独建增益”。E的具体表达式见公式(14)。由于(14)式和(10)式具有对称性,比照命题3,可得如下命题4。 命题4:仅Developing博弈方可改变Developing独建增益E。Developing博弈方可控制的变量有Ai、Ii、α、βi、Wi、di和li,其中E随Ai、α、βi、di和li的增加单调增加,Ii和Wi存在临界点,临界点以下E随两者的增加单调增加,临界点以上随两者的增加单调减少,临界点处取最大值。 由命题3和命题4,可得推论4。 推论4:在承担风险损失成本(即对监管沙盒内的风险承担责任)的情况下,出于提高独建增益B、E考虑,地方政府将会理性控制其建立的监管沙盒内的FinTech创新数量和创新的业务量,不会让其无限度增加。但若不承担风险损失成本,则其出于提高独建增益B、E考虑,将可能无限度增加其建立的监管沙盒内的FinTech创新数量和创新的业务量。 根据表3,结合增益分析,可得如下结论: (一)地方监管沙盒具有较好的可行性。从表3可知,发达地区和欠发达地区地方政府群体演化博弈的最终结果并不收敛于E1(0,0)。因此,地方监管沙盒具有较好的可行性。 (二)欠发达地区监管沙盒仍有一定生存空间。从表3可知,在本文讨论的十五种情形中,有两种情形仅欠发达地区地方政府群体100%选择“实施”监管沙盒,而发达地区100%选择“不实施”;四种情形下,发达地区和欠发达地区地方政府群体均 100%选择“实施”监管沙盒;一种情形下,欠发达地区地方政府可能100%选择“实施”监管沙盒,而发达地区100%选择“不实施”,取决于初始情况。总之,欠发达地区地方监管沙盒仍有一定生存空间。 (三)地方监管沙盒的最终结局具有较高的依存性。在发达地区和欠发达地区均选择“实施”监管沙盒的情况下,两类群体演化博弈的最终结局未必是均100%选择“实施”监管沙盒。依据四个命题及相应推论,最终结局取决于各自的独建增益和共生增益,但独建增益和共生增益除受自身控制外,共生增益还受对方正外部性和负外部性的影响。因此,不管是发达地区还是欠发达地区地方政府,任何一方均无法单方面决定自身监管沙盒的最终结局,两者之间存在较高的依存性。 依据推论1、3、4,建议如下: (一)建议中央层面对地方监管沙盒的质量(尤其是风险发现能力)及监管沙盒内FinTech从业机构的平均风险管理水平进行适度评价,一来缓解地方监管沙盒之间对FinTech从业机构的竞争,二来增加地方监管沙盒的正外部性以对冲FinTech创新给其他地方带来的负外部性。 (二)地方监管沙盒对鼓励FinTech创新、防控金融风险具有重要意义。为避免地方政府逆向选择,建议中央层面明确监管沙盒内FinTech创新产生的风险损失成本应由建设监管沙盒的地方政府承担,以促使其自觉将创新数量和业务量控制在可控范围之内。 综合全文看,本文利用演化博弈模型对发达和欠发达两类地区之间的监管沙盒竞争问题进行了研究,得出了两类地区监管沙盒之间存在较高依存关系等结论,并给出了相关建议。但中国金融监管机构若推出监管沙盒,其与地方监管沙盒之间将是怎样的关系?两类监管沙盒之间将如何协调联动?在“有风险没有及时发现就是失职”之新问责机制下,各类监管沙盒将如何演进?这些问题均有待进一步研究。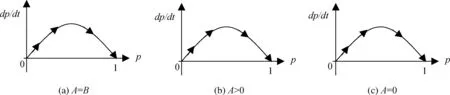
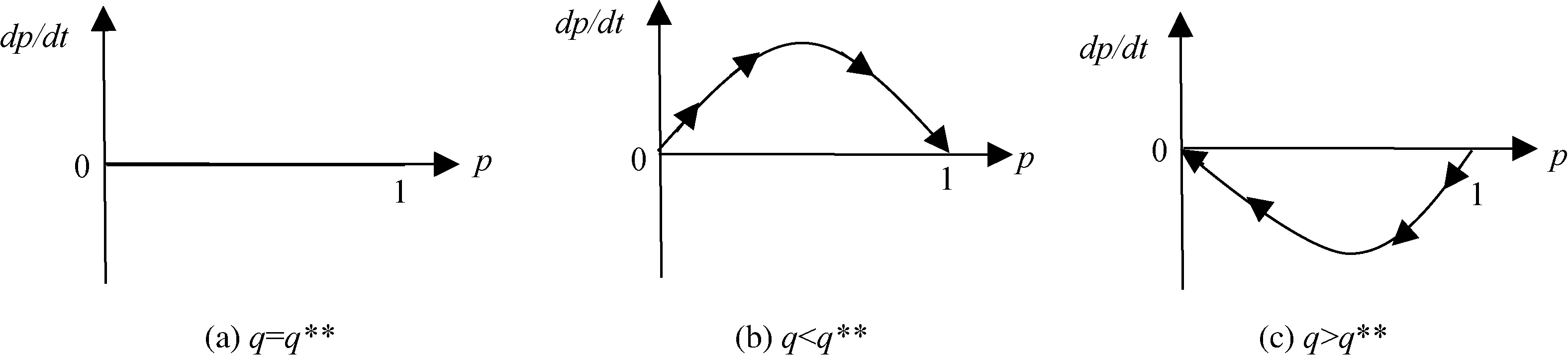
4.3 复制动态的关系及稳定性分析

5 增益分析

5.1 共生增益A、D、分析
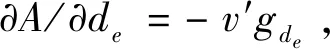
5.2 独建增益B、E分析
6 结语

