基于SolidWorks与Workbench的纤维过滤器壁厚优化设计
孟巧荣,高立志,王 勇,张永锋,王然风
(太原理工大学 矿业工程学院,太原 030024)
在水处理过滤技术中,纤维过滤技术作为一种新兴技术逐渐得到了重视[1],并且在油田油污水和煤矿矿井水处理中得到广泛应用[2-5]。纤维过滤器作为矿用净水站的核心部分,本质的工作原理为压力器。运用弹性失效准则对其进行设计,在设计过程中忽略了不同应力和过滤器失效程度的影响[6]。过滤器在工作过程中不仅受自身重力作用,同时也受内压以及静水压力等不同类型载荷的复合作用,为了保证过滤器的安全可靠,能够承受较大的压力,考虑通过增加过滤器的壁厚来实现,但这样会增加设备的重量,降低机动性, 限制过滤器整体性能的优化以及材料的有效利用,不符合煤矿设备轻量化、经济性要求。随着计算机模拟技术的发展,压力容器的结构优化设计可以在一定程度上弥补传统设计的不足[7],因此,它愈来愈受到煤矿、石油、化工、能源等行业的重视。
本文基于静力学分析理论与优化原理,采用SolidWorks建立参数化模型,利用Workbench的Static Structural计算过滤器的应力分布,在性能约束条件与尺寸约束条件下,通过Screening筛选优化法给出过滤器参数的最优组合,从而减小过滤器壁厚,使材料得到有效利用。
1 纤维过滤器有限元分析
1.1 基于SolidWorks纤维过滤器建模
基于SolidWorks对纤维过滤器进行参数化建模,其尺寸剖视图,如图1所示。其中过滤器球罐上部内、外半径尺寸R1、R2分别为550 mm、562 mm.圆筒内径R3及壁厚d尺寸分别为300 mm、12 mm.在保证其容积的前提下,以球罐内径R1和壁厚d为参数进行参数化建模。
对纤维过滤器参数化模型进行网格划分,通过网格划分将其复杂的参数化模型分为若干简化个体,每个个体之间相互影响,相互制约,形成网格化整体。对简化的网格进行求解计算,得出纤维过滤器在工作过程中所受约束。网格划分有多种,其中最常用的有四面、六面及区域等网格划分法。本文网格划分所采用的方法是六面体网络划分法,该方法能够保证纤维过滤器的计算精确度,六面体网格划分法解决了扫掠及内部空间较大局限问题,并结合四面网格划分法对单元体进行补充,解决了单一四面体的网格划分问题。利用Workbench对纤维过滤器进行网格划分,如图2所示。
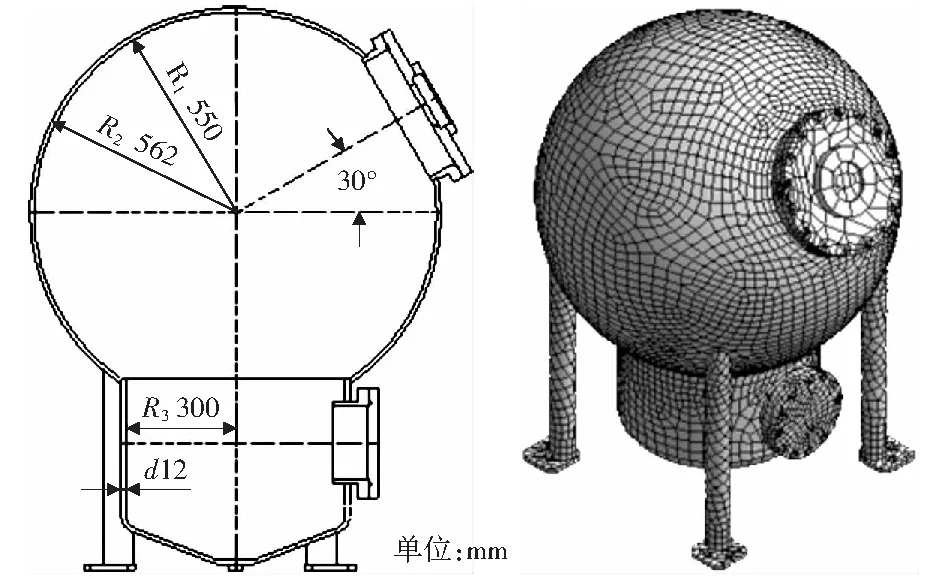
图1 纤维过滤器参数化模型 图2 纤维过滤器网格划分Fig.1 Parametric model Fig.2 Meshing figure
1.2 纤维过滤器应力仿真分析
对纤维过滤器在工作过程中所受应力强度运用仿真软件进行模拟分析,并通过设定密度与重力加速度参数在Workbench力学集成模块中计算过滤器的自重载荷,其中材料密度与重力加速度参数分别设定为7.85×103kg/m3与9.8 m/s2.矿井水密度与其在过滤器中高度有关,影响静水压力。根据已有研究,煤粉与岩粉是悬浮矿井水的主要成分,且其平均密度为(1.3~1.5)×103kg/m3,本文选取密度为1.4×103kg/m3,同时过滤器内水位高度为1 500 mm.
根据GB 50383-2006《煤矿井下消防、洒水设计规范》[8]的相关要求,考虑到井下设备、设施的用水压力,纤维过滤器内压应在1.6 MPa以上,为了避免某些情况下出现的压力突增,给予一定的富余量,纤维过滤器内压设计为2.0 MPa.
在过滤器自重、静水压力及内压的复合作用下,对其应力分布进行求解计算,并将纤维过滤器球罐的支撑柱设置为固定约束。图3为纤维过滤器复合载荷应力分布云图。

图3 纤维过滤器复合载荷应力云图Fig.3 Stress contours of fiber filter on the action of combined load
由图3可以看出,内压决定复合载荷条件下纤维过滤器应力分布结果。在纤维球罐支撑柱与球罐固定位、球罐与圆筒固定位、圆筒底部倒角处、法兰与球罐配合固定位等多处结构都有应力集中。其中在球罐与圆筒固定位应力值最大,为215.54 MPa,远小于材料的强度极限520 MPa.因此需对纤维过滤器的壁厚进行优化,在满足强度条件的前提下,尽可能地减小壁厚,提高材料的利用率,优化过滤器的整体性能。
2 纤维过滤器壁厚优化
2.1 优化设计数学模型
2.1.1设计变量
纤维过滤器上部球罐与下部圆筒分属于内压球壳、内压圆筒,根据GB150-1998《钢制压力容器》[9]相关设计规范:
当pc≤0.4[σ]φ时,内压圆筒的计算厚度:
(1)
当pc≤0.6[σ]φ时,内压圆筒的计算厚度:
(2)
式中:pc为计算压力,取2.0 MPa;Di为圆筒或球壳的内直径,mm;[σ]为圆筒或球壳材料的许用应力,取137 MPa;φ为焊接接头系数,0.9.
经公式计算验证,设计压力值符合算式条件,其中球罐理论计算厚度δ为2.24 mm,圆筒的理论计算厚度δ为2.45 mm.在实际应用中,由于腐蚀失效存在,故在纤维过滤器设计中,留有1 mm的腐蚀裕量。最终球罐与圆筒壁厚值分别为3.24 mm、3.45 mm,近似取整值4 mm.
球罐内径R1∈[550,558],下部圆筒壁厚d∈[4,12].
2.1.2性能约束
304不锈钢材料的力学性能参数如表1所示。

表1 304不锈钢力学性能参数Table 1 Mechanical properties of 304 stainless steel
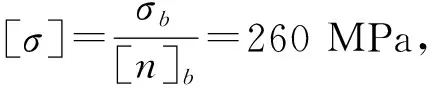
以纤维过滤器总质量Wd为目标函数,确定壁厚优化设计数学模型为:
2.1.3优化设计方法
在Workbench的Direct Optimization中,Screening筛选优化法应用广泛,输入变量可分为离散和连续型两种。采样点数设置决定了参数化计算时间优劣,利用Screening筛选优化方法,适应不同性能的计算机,提高过滤器壁厚优化结果精确度[14-15]。本文优化条件为一个目标、两个变量、三个约束。
计算时间取决于所设采样点数,对于不同配置的计算机具有更好的适应性和精确度,并且满足本设计单目标双变量三约束的优化条件,因此,选择Screening筛选优化方法来优化过滤器的壁厚。图4为优化设计过程。

图4 优化流程Fig.4 Optimization process
以纤维过滤器上部球罐内径R1,下部圆筒壁厚d为设计变量,在SolidWorks中建立纤维过滤器参数化模型,将d、R1参数化导入A(Geometry)中。在C(Direct optimization)中根据数学模型设置2个变量d、R1范围以及目标函数Wd,选取Screening筛选优化法提取变量d、R1值,每一组d、R1值对应一个过滤器模型,并在B(Static structural)中进行网格划分、约束施加、载荷加载,求出对应的等效应力分布云图和目标函数,循环计算,直至找到最佳设计点。
2.2 优化结果分析
2.2.1多变量结构响应曲线分析
通过Workbench的Direct Optimization模块共得到15组设计点,如表2所示。在15组设计点的优化迭代过程中,图5为球罐质量随设计变量变化的响应曲线,图6为等效应力随设计变量变化的响应曲线。
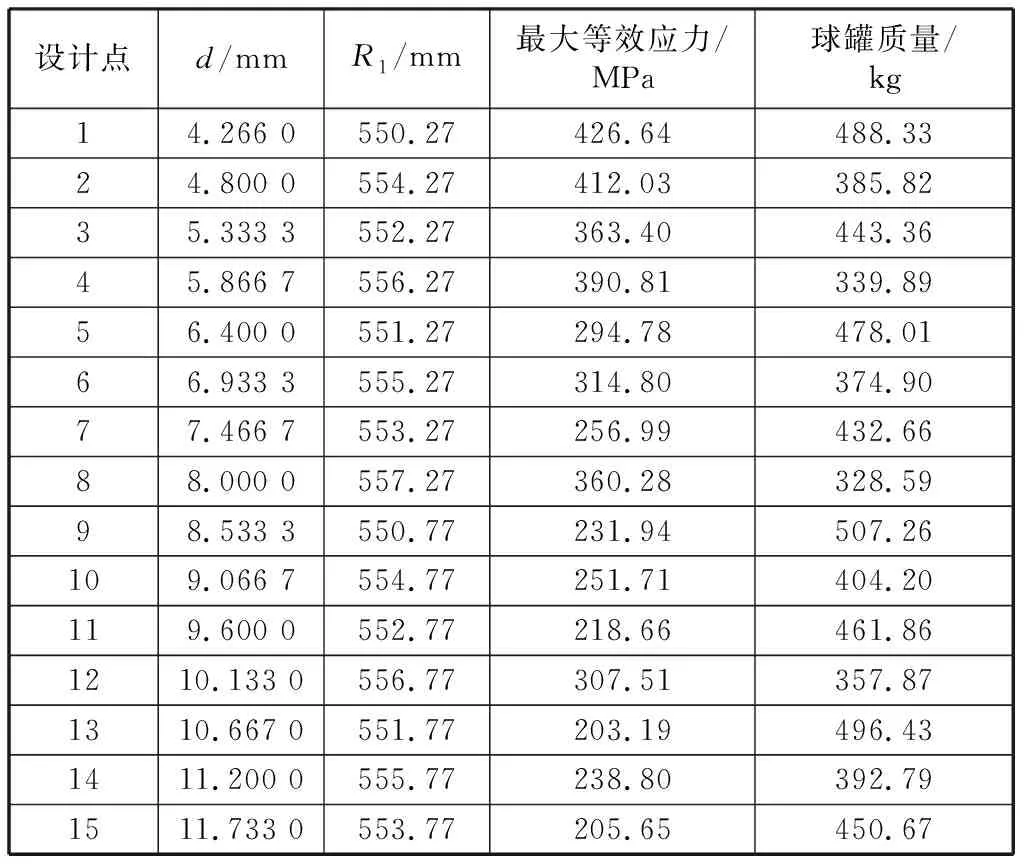
表2 设计点优化值Table 2 Optimal value of design point
通过对图5的分析,发现球罐整体质量曲线随上、下球罐内径R1的不断变化而呈锯齿形变化,与上、下球罐内径R1的变化趋势基本一致,这是由于壁厚d相对于内径R1的变化幅度较小,影响较小,而R1变化幅度决定了纤维过滤器球罐的整体质量。
通过分析,优化过程中过滤器的中效应力峰值呈逐渐下降趋势,满足性能约束的点为9点,但在8点、12点时应力最大值突然增大为557.27 mm与556.77 mm,说明纤维过滤器球罐内径R1>556 mm时,过滤器的中效应力会发生突变,故在设计时应控制在550~556 mm之间。优选过程中,7个设计点满足性能约束条件,其中球罐质量最大值507.26 kg,最小值392.79 kg,等效应力最大值256.99 MPa,最小值203.19 MPa.
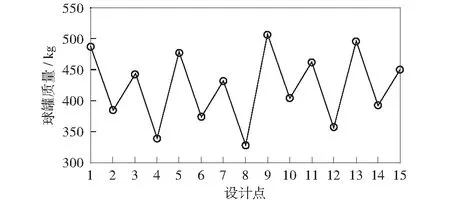
图5 质量变化规律Fig.5 Variation law of tank mass

图6 最大等效应力变化规律Fig.6 Variation law of maximum equivqlent stress
2.2.2多元敏感性分析
通过绘制设计变量灵敏度柱状图,分析了设计变量对纤维过滤器的等效应力及球罐质量影响情况。图7中左边是应力强度,右边是球罐质量,红色表示下圆筒壁厚d,蓝色表示上球罐内径R1.结果表明,在给定的优化范围内,下部圆筒壁厚d对过滤器的最大等效应力有较大影响,对总质量基本无影响,但对上部球罐内径R1却有较大影响,对总质量基本无影响。
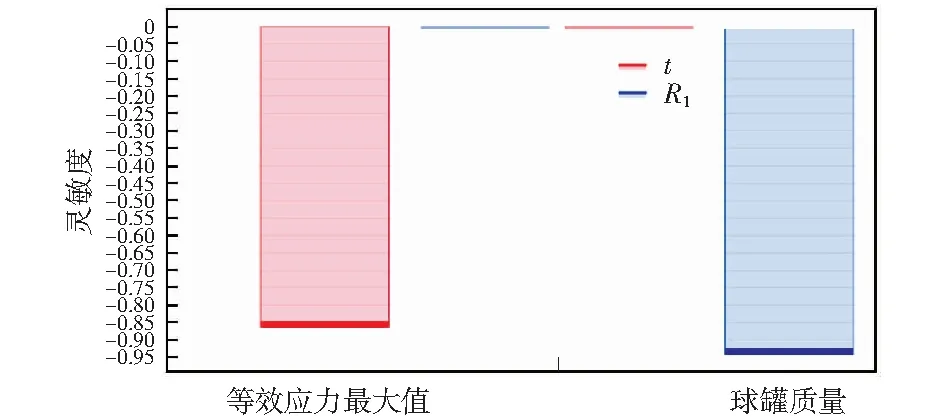
图7 设计变量对过滤罐应力与质量的灵敏度柱状图Fig.7 The sensitivities of design variables to stress and mass of filtering tank
2.2.3目标函数优化分析
表3为基于Workbench参数化模型设计组中筛选出的3个优化候选点。其中星星个数代表优化优劣程度,个数越多其优化性能越好。从表3可以明确得出,候选点1优化结果明显优于其他两点。故在设计约束范围下,候选点1是最优解。表4为优化前后参数对比。从表中可明确得出,优化后纤维过滤器的下部圆筒壁厚d由12 mm降至11.2 mm,减薄了约6.67%,上部球罐内径R1由550 mm提高到555.77 mm,壁厚减薄约48%,球罐总质量由553.15 kg降低到392.79 kg,球罐优化效果明显,质量减少了29%.

表3 筛选结果Table 3 Screening results

表4 优化前后参数对比Table 4 Parameter comparison before and after optimization
3 结论
1) 本文利用SolidWorks建立了纤维过滤器的数值模型,采用Workbench力学计算模块分析了过滤器在静载荷和复合载荷作用下的应力分布特征,确定了纤维过滤器上部球罐与下部圆筒连接部位的最大应力点位置和值,最大应力值为215.54 MPa.
2) 利用Workbench的优化模块对纤维过滤器进行优化,优化原则为满足性能约束的质量最小。在此原则下,下部圆筒壁厚d减薄了约6.67%,上部球罐壁厚减薄约48%,球罐总质量减少了约29%,得出了在变量空间内纤维过滤器结构的最优组合,达到了预期目的。
3) 跟踪分析了优化参数壁厚和内径对纤维过滤器应力和质量的影响,得出了应力强度和总质量的结构响应曲线以及灵敏度柱状图,为矿用纤维过滤器的设计提供了一种新的设计思路,具体的参数可以为实际应用提供参考。

