基于分离系数校正的稀土萃取流程模拟
杨辉,代文豪,陆荣秀,朱建勇
(1 华东交通大学电气与自动化工程学院,江西南昌330013; 2 江西省先进控制与优化重点实验室,江西南昌330013)
引 言
稀土萃取流程模拟是现有工艺流程重组和工艺参数再优化的主要研究平台。20世纪70年代,徐光宪教授在分馏萃取理论的基础上,创建了串级萃取理论[1]。随后,其团队又提出稀土串级萃取过程静态计算和动态模拟计算方法[2-3],为稀土萃取稳态优化和动态仿真提供依据和指导。但是串级萃取理论在处理多组分稀土萃取体系时,易导致大量增根,给程序的计算和判断带来困难,为此,吴声等[2]通过递推-迭代的方法逐级计算各级组分含量,该方法多应用于多出口体系,无法准确计算两出口体系各级组分含量。王振华[4]提出了“等效组分、等效分离系数”法,将多组分等效成两组分计算,但对远离切割位置组分的等效分离系数偏差较大。钟学明[5]在理论分离系数的基础上,以萃取槽水相的平均摩尔分数建立的有效分离系数,在难萃组分的摩尔分数较大(易萃组分摩尔分数较小)时,计算精度较差。丁永权等[6-7]提出相对分离系数模型,推导出稳态下各级组分含量的计算公式,计算速度能够满足稀土萃取全流程优化控制对时间要求,但未考虑实际分离效果,模型输出值和实际值有偏差。文献[8-9]基于简化模型的热力学平衡分析算法,建立了多组分稀土萃取流程模拟,但其仅适用于PC88A 体系萃取稀土的过程。文献[10]从数据驱动的角度出发,利用人工神经网络(ANN)实现稀土溶剂萃取平衡数据模拟,在出现新工况时,流程模拟效果变差。由于稀土萃取工业现场实际应用的萃取槽存在萃取效率,平衡后各级的实际组分含量与基于串级萃取理论分离系数得到的组分含量分布有较大的不同[11],而以上方法均未考虑实际萃取槽萃取效率对理论分离系数的影响,导致模型输出的组分含量和稀土萃取工业实际不符。
由于实际各级萃取槽萃取效率未知,继续通过修正机理模型对萃取过程流程模拟进行研究的做法,往往效果不太理想[12-13],故本文将机理模型和数据驱动的方法相结合,引入分离系数的校正值,使用具有快速收敛到全局最优解特点的斐波那契树优化算法(Fibonacci tree optimization algorithm,FTO)[14-15]对校正值进行求解,实现稀土萃取流程模拟,并通过稀土萃取实际工况改变后的各级元素组分含量值与模型输出值进行对比分析,结果表明本文所建的稀土萃取流程模拟具有较好的动态性能,模型输出值与实际过程各级组分含量吻合。
1 工艺描述和模型建立
1.1 稀土串级萃取工艺描述
分馏萃取可以同时得到两个高纯度、高收率的产品,由于稀土元素间分离系数较小,稀土萃取分离工业通常把若干萃取槽串联起来,使稀土元素与水相、有机相多次接触,从而实现稀土元素间的有效分离[16-17]。图1 描述了具有n级萃取和m级洗涤的稀土串级萃取生产流程,根据稀土元素间不同的化学性质,易萃组分(通常用A 表示)会被萃取到有机相中,分布在每级萃取槽的上面溶液中;难萃组分(通常用B 表示)会被洗涤到水相中,分布在每级萃取槽的下面溶液中。萃取剂从该工艺流程第1级加入,在萃取槽和搅拌力的作用下,从左向右流动;洗涤剂从该工艺流程的第n+m级加入,从右向左流动;料液采用有机相进料的方式,从第n级加入。料液在萃取剂和洗涤剂的作用下,在每一级萃取槽中不断交换和纯化,最后从第1 级得到组分含量为YB的难萃B 产品,从第n+m级得到组分含量为YA的易萃A 产品,为保证稀土萃取出口产品纯度符合生产要求,需要在萃取段和洗涤段各设置一个监测点y1和y2,控制系统会根据监测点组分含量和设定值的差值,对萃取剂流量和洗涤剂流量进行控制调节。
由于稀土萃取实际生产过程中会因为来料产地或批次不同,引起料液的组分不相同,要保证两端出口的产品质量,只有优化工艺参数。另外,稀土企业由于市场竞争等因素需对稀土萃取工艺流程进行重组时,均需要稀土萃取流程模拟平台作为支撑。
1.2 基于分离系数校正的稀土萃取流程模型
由于“分液漏斗法”在处理多组分稀土萃取体系时计算复杂,计算速度难以满足动态仿真的要求,本文选择相对分离系数理论[6]建立各级组分含量的计算模型。
1.2.1 相对分离系数模型 根据串级萃取理论,稀土萃取体系达到稳态时,设Y为有机相组成,X为水相组成,A 为易萃组分,B 为难萃组分,N为组分数。相对分离系数(以β表示)定义为:

因此,可以推导出第i(i=1,2,…,N)组分相对于第一(最难萃取)组分的相对分离系数的表达通式为:

图1 稀土串级萃取生产流程Fig.1 Process flow of rare earth countercurrent extraction

同理,第i(i=1,2,…,N)组分相对于最后(最易萃取)组分的相对分离系数的表达通式为:

由于萃取槽存在一定的萃取效率,实际萃取分离过程中各分离功能段和进料级中相邻组分之间的分离系数并不是相等的,与理论值有一定偏差,相邻分离系数与所处的三种萃取状态:过量萃取、等量萃取(或等量洗涤)、过量洗涤有关。稀土萃取过程的萃取段为过量萃取状态,进料级为等量萃取(或等量洗涤)状态,洗涤段为过量洗涤状态,故稀土萃取体系达到平衡时,相对分离系数的计算公式如表1 所示,表中L为划分难萃和易萃组分的切割位置元素序号,C为当前元素序号。

表1 稀土萃取分离各级中的实际分离系数Table 1 Actual separation coefficient in different stages of rare earth extraction and separation
利用表1 给出的相对分离系数模型,结合工艺指标,可以计算两端出口的组分组成。
1.2.2 两端出口组分组成的计算模型 根据相对分离系数模型和工艺参数、出口指标,得到两端出口的组分组成[18]。有机相出口产品Or 中难萃组分的出口摩尔分数:
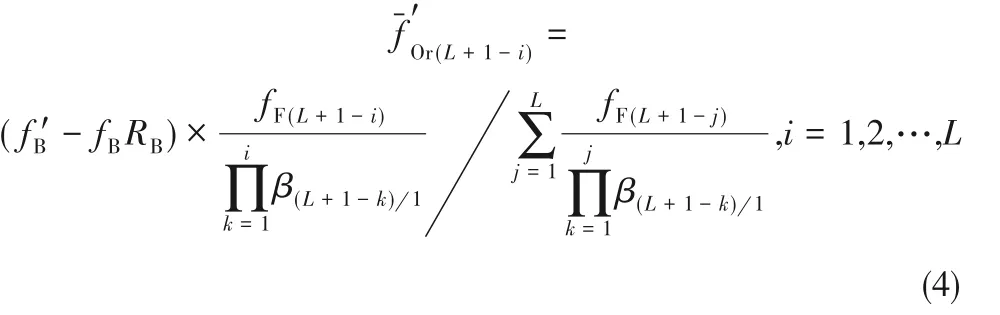
水相出口产品Aq中易萃组分的出口摩尔分数:
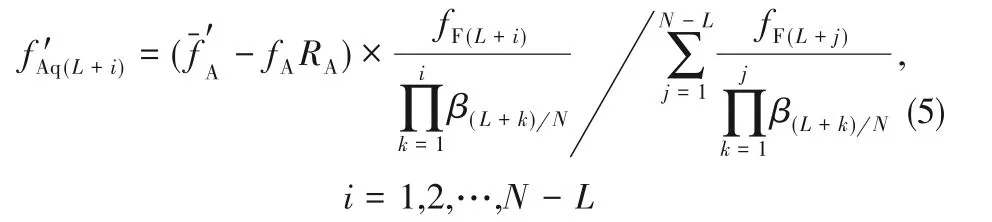
根据进出物料平衡可得,有机相出口中易萃组分的出口摩尔分数:
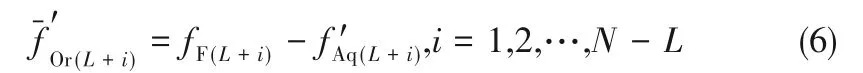
水相出口中难萃组分的出口摩尔分数:

式中,fA、fB、fF分别表示料液中易萃组分、难萃组分和料液中各组分组成,f'表示水相出口各组分摩尔分数,-f'表示有机相出口各组分摩尔分数,R表示产品收率。再对两出口各元素摩尔分数进行归一化处理,即可得到两端出口各元素组分组成。根据1.2.1 节中相对分离系数的表达通式,由两端出口各元素组分组成可以计算出同一级中另一相的组分组成。
1.2.3 同一级两相组分组成计算模型 将相对分离系数通用表达式(2)和式(3)进行转化,可以得到萃取段有机相中组分组成的通用公式:

洗涤段水相中组分组成的通用公式:

基于式(8)、式(9),可以根据分离系数的理论值β计算出每一级中不同相之间的各元素组分含量,但考虑实际工业现场各萃取槽的萃取效率不同,并不能达到理论分离系数理想的分离效果。这里引入理论分离系数的校正值K,则实际的分离系数为K.×β,K为与β同维的向量,“.×”表示向量的各元素对应相乘。运用实际分离系数,式(8)和式(9)可以改写如下。
萃取段有机相中组分组成的通用公式:

洗涤段水相中组分组成的通用公式:

式(10)、式(11)实现了同一级两相间组分含量的计算,稀土萃取达到稳态后,根据各级物料分布情况由物料平衡可以逐级计算出萃取段水相中各组分含量和洗涤段有机相中各组分含量,反复利用式(10)、式(11)和物料平衡可得萃取平衡时各级组分含量。


表2 有机相进料体系的物料分布Table 2 Component distribution of organic phase feed system

洗涤段级间物料传递公式为:

式中,Xj,i和Yj,i分别表示第j级水相和有机相中第i个元素的组分含量。
综上所述,建立了稀土串级萃取达到稳态平衡时的各种关系式,实现了稀土萃取流程模拟,各式中唯一未知变量为理论分离系数β的校正值K,K与稀土萃取的实际情况相关,故需结合智能优化算法对K进行求解,第2节将介绍K的求解方法。
2 分离系数校正值的求解
为了获得稀土萃取流程各级的组分含量值,需确定稀土萃取流程模拟中理论分离系数β的校正值K,本文为了使模型得到的各级组分含量与实际各级组分含量差值的平方和最小,采用最小二乘法来构建最优化目标函数,使用智能优化算法对K值进行求解。
2.1 目标函数建立
为了使模型得到的各级组分含量与实际各级组分含量的差值的平方和最小,将稀土萃取工业实际数值代入式(10)和式(11)中,利用最小二乘法构建最优化目标函数,则萃取段的优化目标为:

洗涤段的优化目标为:

2.2 斐波那契树优化算法
鉴于稀土萃取过程具有多变量、非线性、强耦合等特点[19-20],且每一级萃取槽不同组分间的分离系数都有一个校正值,因此多组分稀土萃取体系的优化目标具有多峰多变量的特点,然而传统的智能优化算法及其改进算法,如遗传算法(GA)、粒子群优化算法(PSO)等,在求解这种多峰函数最优解时存在易陷入局部收敛的问题[21-24]。基于对抗原刺激的适应性免疫反应的基本特征提出的免疫克隆算法(CLONALG)[25]以及能够实现动态优化、改进鲁棒性的人工免疫网络算法(dopt-aiNet)[26]等算法具有较强的多峰寻优能力,但这类算法在某些参数的设置不合理时,无法取得全局最优解,最终导致寻优结果精度不高、易陷入局部收敛。多变量优化算法(MOA)[27-28]具有的多组特性,使该算法在求解多变量函数时取得了良好效果,但由于算法结构限制,处理多峰函数能力不强。基于斐波那契法最优化原理与黄金分割法提出的斐波那契树优化算法,可以快速收敛到多峰函数的全局最优解,且其全局最优解的可达性为1。FTO 在求解这种多峰多变量复杂过程全局最优解时,不易陷入局部最优解,具有良好的可达性指标[29]。为了得到校正值K,本文采用FTO对其值进行参数优化。
2.2.1 斐波那契法最优化原理 对于求解一维单峰函数优化问题,在使用分割法生成试探点进行n步搜索的最优方案中存在斐波那契数列,该数列{Fn}的计算公式为:

上述n步斐波那契方案通过按一定比例逐步压缩搜索区间,令区间内的当前点不断逼近最优解[30]。该比例为:

由斐波那契数列性质知,斐波那契压缩比例α线性收敛于黄金分割数,该方案为唯一最优方案。
2.2.2 分割点的计算公式 FTO在斐波那契法基础上扩展到n维空间,并引入搜索解的随机性。多组分稀土萃取过程理论分离系数的校正值K和分离系数β同维,维度为组分数N,令K=[k1,k2,…,kN],k1=1,ki∈(0,1),i= 2,3,…,N,Ka和Kb为K取值的上下限,上下限值根据规则随迭代次数更新,Kg为分割点,3个向量在欧式空间中满足式(18):

式中,Fi为斐波那契数列的第i项,两个端点应满足J(Ka)≤J(Kb)。Kg的计算方式如下:
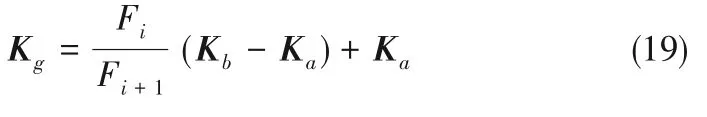
2.2.3 算法迭代规则 设FTO 当前处理的点集为M,集合大小满足斐波那契数Fi(i=1,2,…,Q),Q为斐波那契树深度。根据斐波那切数列的特点,初始化搜索点集的大小通常选择为FP(Q>P≥3),P为斐波那契树嵌套深度。用两个迭代规则构造斐波那契树,更新当前点集M,分别实现全局搜索和局部搜索,既保证收敛精度,又保证收敛速度。
规则1令基本结构中的端点Ka等于当前处理的点集M,在全局范围内随机产生端点Kb,Kb各元素生成规则满足自变量取值范围内的均匀分布的随机变量,Kb元素的个数满足当前的斐波那契数,根据式(19)求解出分割点Kg。
规则2令基本结构中的端点Ka等于当前处理的点集M中的最优解,端点Kb为M中除去Ka的其他值,根据式(19)求解出分割点Kg。
执行完规则1和规则2,得到2Fi个新增点,加上当前点集M的Fi个点,共有3Fi个点,比较这些点的适应度值,保留前Fi+1项较优解,丢弃其余解,更新点集M,同时集合大小更新为Fi+1。规则1 完成全局搜索过程,规则2完成局部搜索过程,保证了FTO 的最优解可达性和收敛速度。
2.2.4 算法流程 运用FTO算法对校正值K求解的流程图如图2所示。
根据图2,具体步骤如下:首先,初始化树结构定义嵌套深度P和树深度Q,在校正值K的取值范围(0,1)内,随机产生一个大小为FP,满足(0,1)内均匀分布的初始解集合M,再根据规则1和规则2生成分割点,逐步生成斐波那契树,直到集合大小为FQ,从中选出J(K)最小的FP个解,得到当前迭代的最优集合M,并以此集合作为下次迭代的初始集合,继续生成斐波那契树,直到达到最大迭代次数或目标满足终止条件,则从最优集合M中选择最优解作为萃取槽理论分离系数β的校正值。
2.2.5 算法可达性证明 针对多组分稀土萃取体系的优化目标具有多峰多变量的特点,设目标函数的解集为K⊂RN,N为组分数,即解的维数,最优解K*∈K。根据FTO 算法规则1,在解范围内随机产生端点Kb∈K,Kb=(k)N×1满足解范围内的均匀分布,即(k)N×1~U(kmin,kmax),则Kb在取值范围内满足:

图2 FTO算法求解校正值K的流程图Fig.2 Flow chart of FTO solving K

由式(20)可知,必存在一正整数Imax,使得当算法的迭代次数大于Imax时,搜索到的当前解K*,使J(K*)最小,即当前解K*为最优解,所以,斐波那契树优化算法求解多组分稀土萃取体系优化目标的可达性为1。
3 稀土萃取流程模拟系统的实现及仿真验证
首先,结合江西某稀土萃取分离公司的生产现场实际数据,运用FTO 对理论分离系数β的校正值K进行优化求解,分析各级分离系数校正值符合萃取工业实际,验证了引入校正值是合理的、有效的;然后,运用MATLAB GUI 开发稀土萃取流程模拟系统;最后,为了验证当萃取实际工况发生改变时稀土萃取流程模拟系统的有效性,使用只改变进料料液组成时的生产现场实际数据和该系统计算数值进行对比验证,结果表明本文所建流程模拟系统符合实际工况。
3.1 校正值K的求解和验证
本文以江西某稀土萃取分离公司CePr/Nd 萃取分离生产线为研究对象,从生产现场获得包含入矿条件、生产指标和稳态下各级组分含量值的数据。其中,料液组成及主要工艺参数如表3所示。

表3 CePr/Nd萃取过程主要工艺指标Table 3 Main process indexes of CePr/Nd extraction process
考虑斐波那契数列的性质,数列前三项数值较小,斐波那契树嵌套深度P至少从4 开始选择,斐波那契树深度Q最大取10,此时集合大小为F10=55。本文列举最大迭代次数为2000,P-Q取不同值时,对目标函数式(14)和式(15)各求解10次,得到目标函数的最小值(MIN)、最大值(MAX)、均值(MEAN)和标准差(STD),计算结果如表4所示。
由表4 可知,P-Q取值为6-8 时,FTO 优化求解效果最好,本文在求取校正值K时,设置斐波那契树嵌套深度P为6,斐波那契树深度Q为8,迭代次数为2000。由于相对分离系数模型中第一组分Ce 相对于Ce 的分离系数设置为1,所以其校正值也设置为1,这里只需求解另两个分离系数的校正值,设Ce/Pr 分离系数的校正值为k1,i∈(0,1),Pr/Nd 分离系数的校正值为k2,i∈(0,1),i表示萃取槽的级数。稀土萃取过程每一级使用FTO优化算法对系数K进行寻优求解10 次,每一级各得到10 个k1和k2值,取k1的平均值作为Ce/Pr分离系数的校正值,k2的平均值作为Pr/Nd 分离系数的校正值。经过计算得到各级系数如图3所示。
由图3 可知:(1)萃取段Ce/Pr 分离系数的校正值的范围为[0.8261,0.9268],萃取段Pr/Nd 分离系数的校正值的范围为[0.8915,0.9607],洗涤段Ce/Pr 分离系数的校正值的范围为[0.5026,0.5107],洗涤段Pr/Nd 分离系数的校正值的范围为[0.8512,0.9703];(2)萃取段这两个校正值在第1~10级存在轻微波动并呈下降趋势,这与多组分萃取体系的难萃组分的组分含量在萃取段存在一定波动相关;(3)校正值第10~26级呈现增大趋势,说明在进料级附近,萃取槽的分离效果要好于两端出口级;(4)洗涤段Ce/Pr分离系数校正值较小是由于多组分体系难萃组分在洗涤段处于过量洗涤状态,Ce、Pr 两种难萃组分的实际分离系数接近于1,其理论分离系数值为2.05,符合实际;(5)洗涤段Pr/Nd分离系数的校正值呈下降趋势,同样也说明在进料级附近,萃取槽的分离效果要好于两端出口级。故本文引入的分离系数校正值是合理和有效的,本文的模型符合实际工业过程。

表4 FTO选取不同参数的性能指标Table 4 Performance indexs of FTO with different parameters

图3 各级系数计算值Fig.3 Calculated values of coefficients at all stages
3.2 稀土萃取流程模拟系统的设计和实现
为使稀土萃取分离企业工程师更好地掌握稀土萃取状态,本文结合MATLAB GUI,将本文模型进行软件实现,开发稀土萃取流程模拟系统,系统的结构如图4所示。

图4 稀土萃取流程模拟系统结构图Fig.4 Structure diagram of rare earth extraction process simulation system
稀土萃取流程模拟系统包含登录模块、数据读取和校验模块、数据计算模块以及数据显示和存储模块。登录模块限定指定用户才能使用该系统;数据读取和校验模块可以获取用户输入的料液组成信息、萃取体系信息、产品指标以及各功能段级数等数据,并自动校验用户输入数据的合法性和正确性。根据用户输入数据,数据计算模块计算得到稳态下各级组分含量;数据显示和存储模块则能够实时存储数据和结果显示。
用户登录稀土萃取流程模拟系统后,显示的主界面如图5 所示,流程模拟系统能够根据用户输入快速直观地给出萃取平衡时各级组分含量,为稀土分离新工艺开发和稀土萃取优化控制提供重要的参考。

图5 稀土萃取流程模拟系统界面Fig.5 Main interface of rare earth extraction process simulation system
稀土萃取流程模拟系统的主界面主要包含料液组成、产品指标和生产工况等参数的设置,以及显示稳态下各级各组分含量,通过设置不同组分序号实现任意组分的稀土萃取工艺计算,实现多组分两出口体系稀土萃取流程模拟。比如CePr/Nd 萃取体系时,设置第一组分序号为2,切割位置序号为3,最后组分序号为4,即可实现CePr/Nd 萃取体系的流程模拟。
稀土萃取流程模拟系统启动后,当料液组分发生改变时,用户将新的料液组成输入该系统,模拟仿真结果中会动态显示稳态下各级组分含量值,实现稀土萃取流程模拟,减少工业现场实验耗费的时间、人力、资源成本。
3.3 稀土萃取流程模拟系统动态性能的仿真验证
稀土萃取实际生产过程中往往是因为来料批次不同,料液的组分组成就不相同,使稀土萃取工况发生改变。为验证当工况改变时稀土萃取流程模拟系统的动态性能,从生产现场获得料液组成改变时的各级组分含量值,工况改变后的料液组成如表5 所示,其他工艺参数和表3 保持一致,用本文的稀土萃取流程模拟系统计算各级组分含量与实际值进行比较,验证动态性能。
运用稀土萃取流程模拟系统计算各级组分含量和实际组分含量对比,如图6所示。
由图6 可知,本文的稀土萃取流程模拟系统计算出的各级组分含量值和实际值基本一致,能够真实反映稀土萃取各级组分含量的分布情况。

表5 CePr/Nd萃取过程料液组成Table 5 Component of feed in CePr/Nd extraction process

图6 本文流程模拟系统计算的各级组分含量值和实际值对比Fig.6 Comparison between content calculated by process simulation system and actual values
为了说明稀土萃取流程模拟系统的准确性,将流程模拟系统计算出来的数据和工业现场实际数据进行比较,采用平均相对误差(MEANRE)、最大相对误差(MAXRE)和反映计算数据偏离实际值程度的均方根误差(RMSE)作为该系统的评价指标。平均相对误差、最大相对误差和均方根误差的计算公式如式(21)~式(23)所示。

其中,z为流程模拟系统计算出的数据,z*为实际工业现场数据。计算结果如表6 所示,各级组分含量的相对误差的绝对值如图7所示。

表6 流程模拟系统的性能指标Table 6 Performance standard value calculated by process simulation system

图7 流程模拟系统计算后各级各组分含量的相对误差的绝对值示意图Fig.7 Absolute value of relative error of each component content after calculation of process simulation system
由表6 和图7 可知,当进料发生改变时,流程模拟系统得到的各级组分含量都与实际值非常接近,各级组分含量的最大相对误差的绝对值在5%以内,较大的相对误差绝对值点发生在两个出口端,且产生较大误差的元素都是组分含量较小的元素。这是由于组分含量较小,所以不论是获得的实际数据,还是计算得到的理论数值如果有轻微的误差,就会导致一个大的相对误差的绝对值。故本文提出的分离系数校正值也能保证在实际工况发生改变时本文流程模拟的合理性。
4 结 论
由于稀土萃取分离中的萃取槽存在一定的萃取效率,而传统基于机理的稀土萃取流程模型未考虑萃取效率对分离系数的影响,难以满足实际稀土萃取流程模拟的要求。本文在基于相对分离系数的稀土萃取模型基础上,对机理模型中分离系数进行校正,并利用FTO 优化算法对该系数进行优化求解,开发了稀土萃取流程模拟系统,实现了符合实际生产工况的稀土萃取流程模拟。通过仿真测试,表明该系统在稀土萃取工况发生变化时,由流程模拟系统得到的各级组分含量接近萃取生产现场实际值,能够真实地反映稀土萃取流程,可为实现现有稀土萃取全流程优化重组或工艺优化控制提供重要支撑。
符 号 说 明
A——易萃组分
Aq——水相出口产品
B——难萃组分
Fi——斐波那契数列的第i个元素值
f——料液组成
f'——水相出口分数
G——水相中各组分质量总和
K——分离系数的校正值
L——划分难萃组分和易萃组分的切割位置的元素序号
M——FTO当前处理的最优解集合
m——洗涤段级数
N——组分数
n——萃取段级数
Or——有机相出口产品
P——斐波那契树嵌套深度
PA,PB——出口产品纯度
Q——斐波那契树深度
R——产品收率
W——洗涤量
Xi,j——第i级水相中第j个元素组分含量组成
Yi,j——第i级有机相中第j个元素组分含量组成
α——斐波那契压缩比
βi/j——第i组分相对于第j组分的分离系数

