增值评价中缺失数据对线性回归模型成绩预测的影响

徐路明 杨亚坤

一、问题提出

教育质量评价仅以终结性评价为标准对于不同学校群体有失公允，对学校的教学积极性也是不利的，需要更加科学和准确地评价学校和教师的效能。《教育部关于推进中小学教育质量综合评价改革的意见》中提出要改进评价方式方法，要通过直接考查学生群体的发展情况评价学校的教育质量，注重考查学生进步的程度和学校的努力程度，改变单纯强调结果不关注发展变化的做法[1]；《中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》中再一次强调了要健全质量评价监测体系，强化过程性和发展性评价[2]。《温州市中小学教育质量增值评价实施指导意见》中提出，要关注评价的起点和过程，切实解决因起跑线不同带来的评价偏差[3]。基于此，一些地区在对学校的教学质量评价中引入了增值评价，以学校为单位，用以判断教学质量的提升程度。学校效能增值性评价的出现源于美国《关于教育机会平等性的报告》[4]。增值评价是指通过追踪研究设计，收集学生在一段时间内不同时间点上的标准化测验成绩，基于学生自身测验成绩的纵向比较，并考虑其他不受学校或教师控制因素对学生成绩的影响 （如学生的原有成绩水平、人口学因素、家庭背景信息以及学校周围地区的经济发展水平等）[5]。

增值性评价作为关注学生自身进步与发展的一种方法，不同于以往的终结性评价，也不单单是对学业质量进行一个横向的比较，它是实现发展性评价的重要手段之一。现有的增值评价研究包括对国际上增值评价的介绍，例如，徐丹和牛月蕾就对美国田纳西州的教育增值评价模式进行了介绍[6]。也有学者运用多水平分析模型对学校效能进行增值评价，如杜屏和杨中超运用两水平模型对农村初中学校的效能进行增值评价，探讨了学生水平、学校水平对学校效能的解释力[7]。马晓强、彭文蓉和萨丽·托马斯运用增值评价对河北保定市高中学校进行效能判断，研究发现60%～80%的高考成绩校际差距都不是学校教育教学差异所导致的， 生源、学生背景、学校背景解释了绝大多数的差异，在提高学生进步幅度方面，不同学校间存在明显差异[8]。大学时期增值评价的研究在评价内容、方法上则更为复杂，学生在大学期间增值的维度较多，关键维度和指标的选取及测试方法的操作性、应用性有待进一步完善[9]。除了一般统计模型方法，杨志明、贾立新和吕龙梅还将心理等值的技术运用到增值评价中，从而更好地对阅读能力进行评价[10]。 王光秋在四维绿色评价体系中引入了增值评价[11]。

可以看到，增值评价的研究与应用都在不断丰富，在应用的学段上，既有义务教育阶段的，也有高中、高等教育阶段的；在运用的模型上，既有概要分析、一元回归分析、多元回归分析，也有多水平分析模型；在评价维度上，既有基于学业的一元增值评价，也有包括学业、品德、身心健康等的多元评价。

然而，在基层（区、县）实际应用中，在对学校学业成绩增值情况进行评价时，由于学生转学、回生源地参加中、高考等原因导致区域、学校层面的入口出口数据不完整，在不能把全区（县）所有的学生都纳入建模样本时，用构建后的模型进行成绩预测的可靠性如何，每个学校运用该模型进行成绩预测的误差如何？研究表明，当缺失值的比例超过60%时，数据完全失去了可利用的价值[12]。 在对学校的学业成绩进行预测时，缺失比例达到多少会对学校最后的增值排名产生影响？ 在不同的样本量下，上述情况又会有何不同呢？区域内学校水平分布是否会对学校增值产生影响？

本研究使用线性回归模型来构建学生入学成绩和毕业成绩的关系，以学校为单位，用入学成绩来预测其毕业成绩，将预期值与实际毕业成绩相减得到每个学校的增量，如图1 所示。线性回归分析包括一元线性回归分析和多元线性回归分析等，它是一个因变量与一个或多个自变量之间的线性关系常用的统计方法，这一方法是估计观测值与期望值之间残差值的标准统计技术[13]。 在基层（区、县）评价机构或教学一线使用时，一元线性回归模型原理通俗易懂，更容易被理解、接受，且区（县）层面样本量相对市、省级小，缺失数据对其影响更大，故本研究选用一元线性回归模型作为研究载体。

图1 学校增值情况线性回归模型

二、模拟研究

1.研究目的

本研究拟通过设定不同的缺失比例，比较不同样本量大小和学生入学成绩是否存在差异等因素对学校增值效能排名的影响。

2.研究方法

本研究为4×3×2 的混合设计，缺失比例设置4个水平：5%、10%、30%、60%， 样本量设置3 个水平：2000 人、5000 人、10000 人， 学校设置两个水平：均衡（即不同学校学生成绩随机生成）、不均衡（即不同学校学生入学成绩按从小到大排序生成）。其中，学校水平差异为被试内变量，缺失比例、样本量为被试间变量，学校数量固定为20 所。

本研究为模拟研究，通过mvrnorm 函数生成服从多元正态分布的两列数据，两列数据的相关系数r 为0.9，均值为70，标准差为15，并在此数据的基础上随机缺失1000 次。

3.评价指标

结果分析指标包括学校排名变化总量、排名变化量/校、整体回归系数的ABS、SD 值。完整的数据集和缺失的数据集里每个学校的增值量均可计算，根据增量每个学校会获得一个名次，排名变化总量为所有学校在完整、缺失两种情况下相差名次的总和； 排名变化量/校指排名变化总量与发生排名变化的学校数量之比， 上述两个指标均为随机缺失1000 次结果的均值；整体回归系数的ABS、SD 值计算公式如下（以A 系数为例），N 为1000 次：

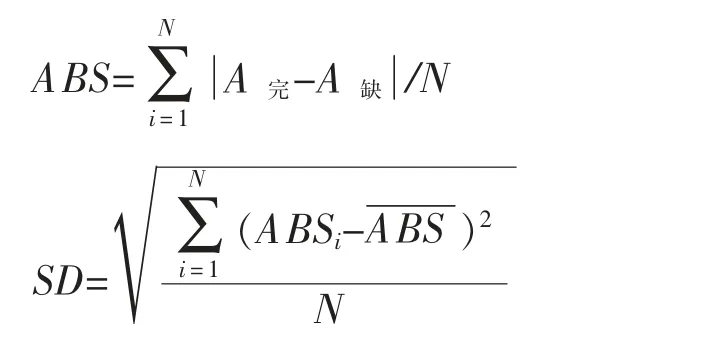
三、研究结果

1.缺失比例与样本量对学校排名的影响

表1 和表2 分别呈现了不同学校水平分布下，缺失比例和样本人数对学校增值排名的影响。从表1 可以看出，在学校水平均衡时，缺失比例与样本量均对学校排名变化有影响。当缺失比例从5%增加到60%时，学校排名变化总量从2 个名次上升到6 个名次，平均每所学校的排名变化从0.63 个上升到1.40 个名次，均在1 个名次左右。在不同的缺失比例下，随着样本量的增加，学校排名变化总量和每所学校排名变化量均呈现下降的趋势。

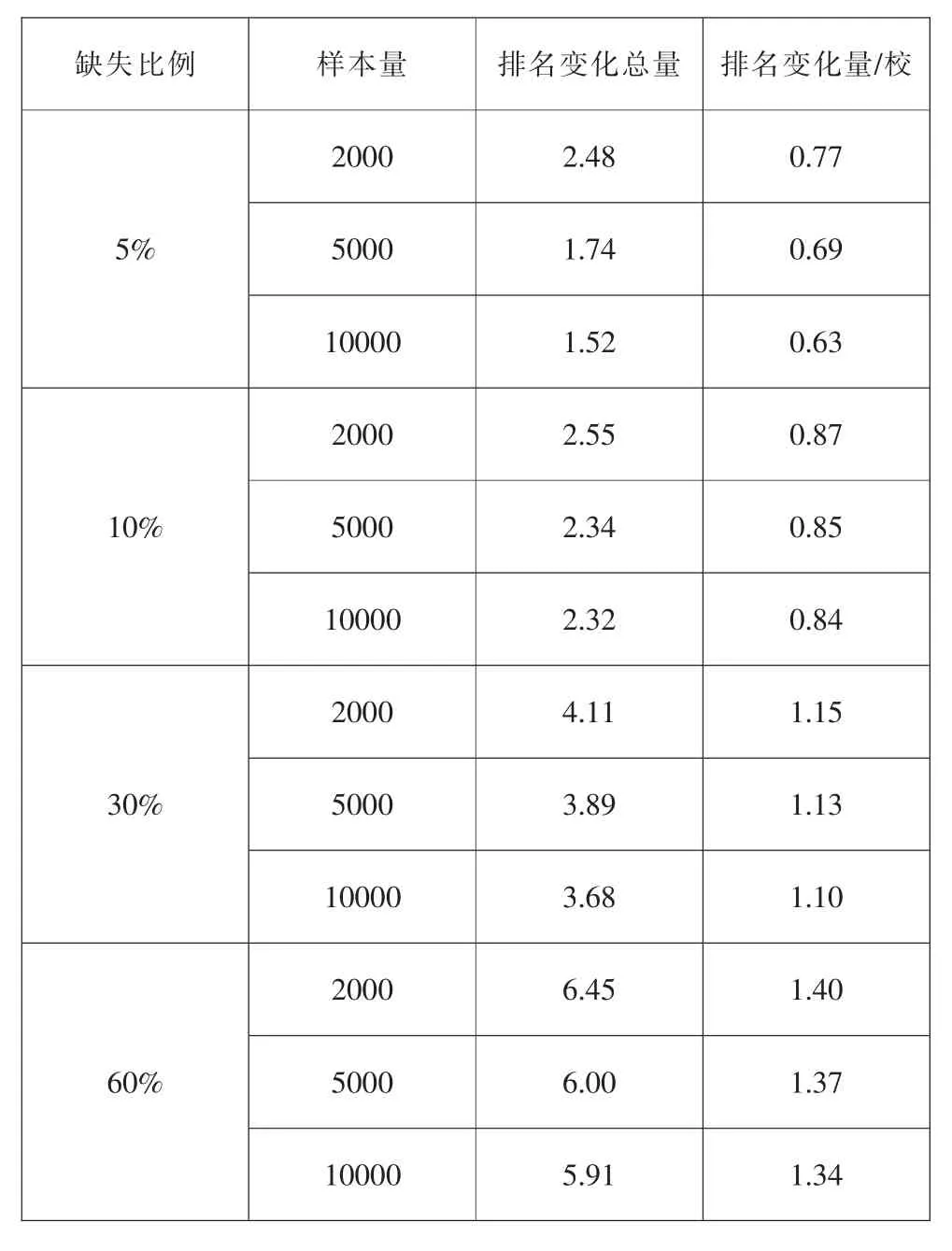
表1 缺失比例与样本量对学校排名的影响（学校水平均衡）

从表2 可以看出，当学校水平不均衡时，随着缺失比例的增加，学校排名变化总量和每所学校排名变化量仍呈递增的趋势。当缺失比例从5%增加到60%时， 学校排名变化总量从5 名增加到12名，且每所学校排名变化均量从1 名增加到2 名；但样本量的影响不太明显。 相比学生入学成绩无差异，此时排名变化总量和每所学校排名变化量有所增加。

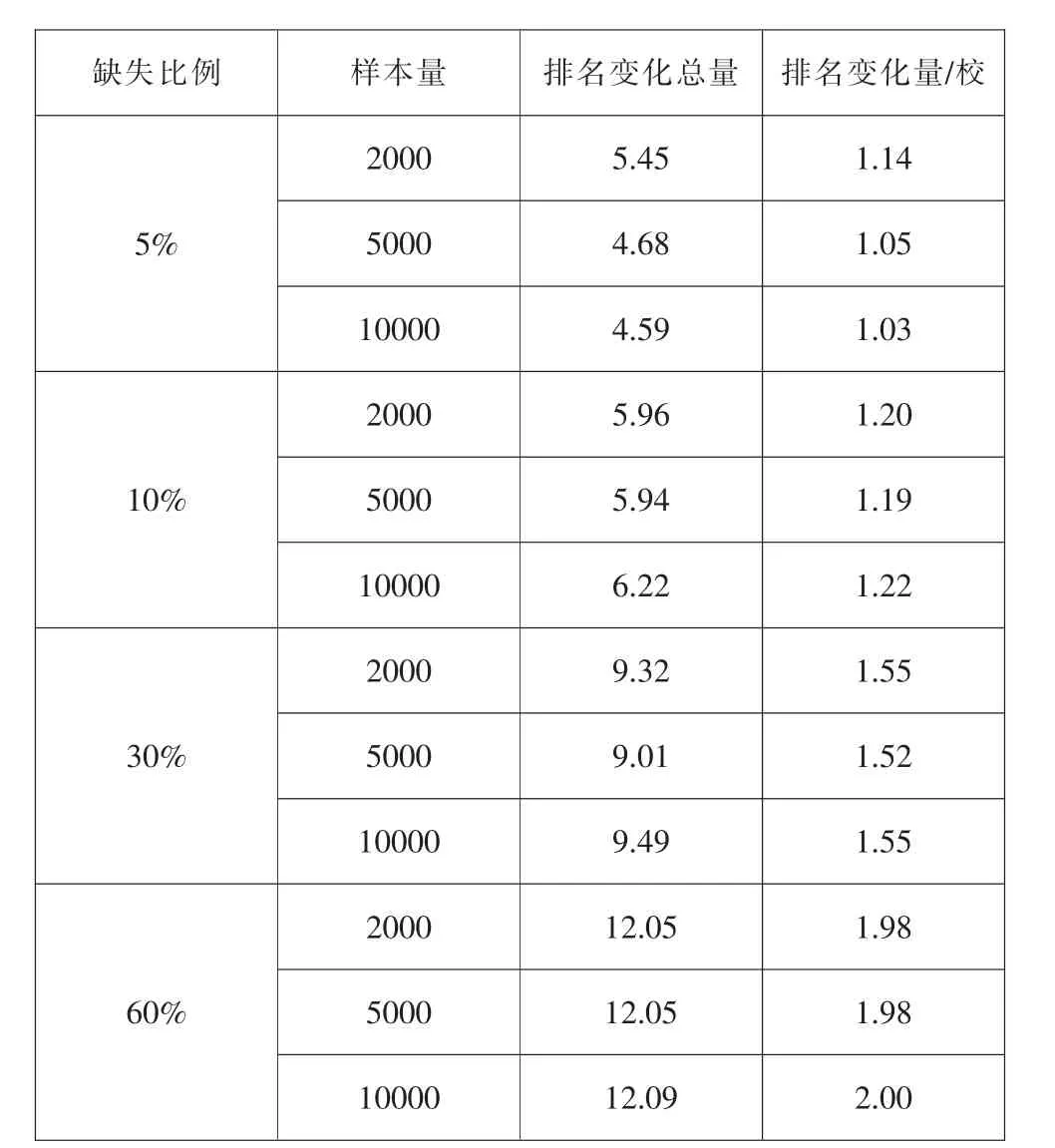
表2 缺失比例与样本量对学校排名的影响（学校水平不均衡）

2.缺失比例与样本量对回归系数的影响

表3 和表4 分别呈现了不同学校水平分布下，缺失比例和样本人数对回归系数返真性、稳健性的影响。从表3 可以看出，随着缺失比例增加，在学校水平均衡时，回归方程的A 和B 值在ABS 和SD 指标上呈现出递增的趋势，A 值的ABS 值从0.0008增加到0.0091，SD 值从0.0006 增加到0.0071；随着样本量增加，A、B 值的ABS 和SD 指标呈现出递减的趋势。

从表4 可以看出，当学校水平不均衡时，随着缺失比例和样本量的改变，A 和B 系数的ABS 和SD 指标的大小与学校水平均衡时相差不大， 且呈现出与学校水平均衡时相同的变化趋势。

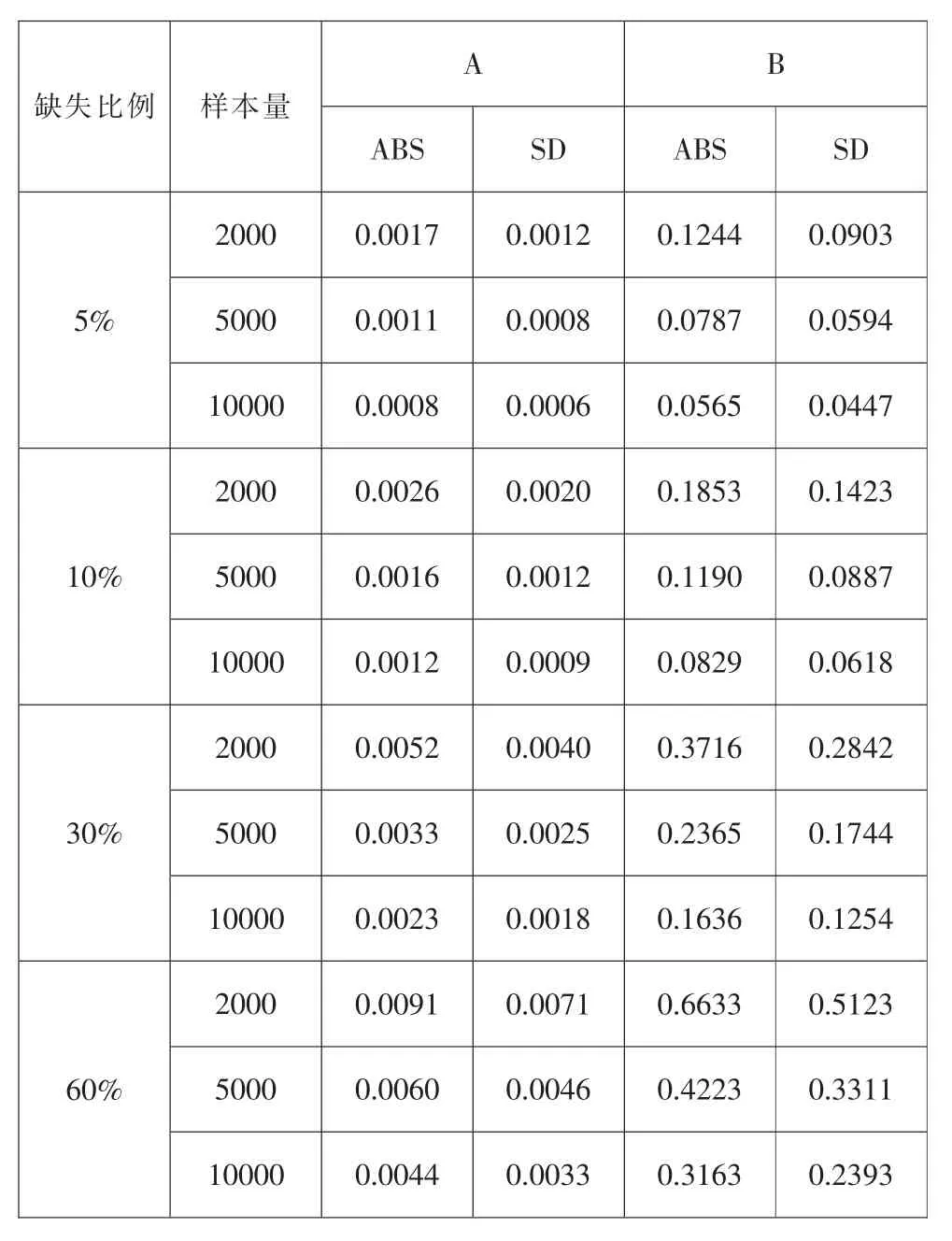
表3 缺失比例与样本量对回归方程的影响（学校水平均衡）

表4 缺失比例与样本量对回归方程的影响（学校水平不均衡）

四、讨论

1.缺失比例对学校增值的影响

在学校水平均衡时，随着缺失比例的增加，学校增值评价排名的误差也逐渐增加。缺失比例的增加会使得可获得的数据信息减少，从而使得回归线越来越偏离真实回归线。在学校水平均衡时，随着缺失比例的增加，学校平均名次变化维持在1 名左右，但学校排名变化总量呈现递增的趋势。当缺失比例为5%时，学校排名变化总量为2 名左右，当缺失比例上升到10%时， 学校排名变化总量变化不大。 若区域内学校水平相差不大， 且缺失比例在5%、10%左右时，可考虑继续使用增值评价。 当缺失比例继续上升到30%、60%时， 学校排名变化总量上升到4 名、6 名左右，误差相对来说增大。

在学校水平不均衡时，学校增值的误差相对学校水平均衡时增加。 但就回归系数而言，在某一固定缺失比例下，学校水平是否均衡对于整体的回归系数影响不大。 这可能是因为在学校水平均衡时，每个学校都是总体的一个代表性样本，学校回归系数与整体回归系数差异较小； 而学校水平不均衡时，每个学校学生成绩分布较为集中，学校回归系数与整体回归系数差异较大，故在学校水平不均衡时，学校增值误差相对较大。随着缺失比例的增加，平均每校名次变化和学校排名变化总量也呈现出递增的趋势。当缺失比例为5%时，学校排名变化总量为5 名左右，平均每校名次变化为1 名；当缺失比例为10%时，学校排名变化总量变化不大，为6名，平均每校名次变化仍为1 名。 若区域内学校水平相差较大，且缺失比例在5%、10%左右时，可根据区域实际情况来判断是否继续使用增值评价。当缺失比例继续上升为30%、60%时， 学校名次变化总量和平均每校名次变化量增加较多，学校名次变化总量分别为9 名、12 名，平均每校名次变化均为2 名左右。

2.样本量对学校增值的影响

随着样本量的增加，学校增值评价排名的误差呈递减的趋势，但这种趋势在学校水平不均衡时并不明显。总体来讲，样本量对学校增值评价排名有一定的影响，因为在相同缺失比例下，学生数量的增加会使得计算获得的信息增加， 但这种影响较小。如当学校水平均衡、缺失比例为5%时，当样本量从2000 增加到10000， 学校排名变化总量从2.48 名下降到1.52 名， 但仍然维持在2 名左右，学校排名变化/校从0.77 名下降到0.63 名； 缺失比例为10%时， 学校排名变化总量从2.55 名下降到2.32 名， 误差量没有像缺失比例那样发生质的变化。

五、结语

总而言之，样本量、缺失比例、学校水平分布均会对最终学校的增值情况产生影响。学校水平不均衡时，相同条件下，误差会大于学校水平均衡时的情况。样本量在2000-10000 之间时，不同的样本量影响不大。 区域缺失比例在5%、10%左右时，结果如上所示，相对来说误差不大，尚可接受，但各区域需按照本区域的实际情况与误差情况接受度，来做出相应的判断和决定。