小电流接地系统铁磁谐振过电压关键影响因素辨识*

何 龙 马金财 杜龙基 李 军 吴伟丽 刘 勇

(1. 国网新疆电力有限公司昌吉供电公司 昌吉 831100；2. 西安科技大学电气与控制工程学院 西安 710054；3. 安徽正广电电力技术有限公司 合肥 230000；4. 大连理工大学电子信息与电气工程学部 大连 116024)

1 引言

我国配电网多采用中性点不接地方式，配有电磁式电压互感器时，电力部门在设计时会注意避免产生铁磁谐振问题。然而近年来，随着配电网的建设和发展，小电流接地系统在互感器母线空载合闸或单相铁磁谐振后，出现了铁磁谐振事件频繁发生的现象，造成电压互感器一次线圈中通过相当大的电流。当一次侧熔断器尚未熔断时，可能使电压互感器烧毁；当一次侧熔断器熔断时，则使变电所的值班人员无法读取系统的正确电压值。此外，铁磁谐振所产生的过电压还会对电力设备安全运行构成严重威胁。

国内外的专家学者对铁磁谐振进行了大量的研究，包括理论分析、各种试验以及仿真等，从不同角度解释电压互感器(Potential transformer，PT)铁磁谐振的现象及其变化规律，并提出一系列抑制铁磁谐振的措施，研制相应的装置，在实际工程中也取得了一定的效果。不过，上述措施都存在仅对铁磁谐振故障进行事后补救而非提前预防的局限性[1]，若能从铁磁谐振发生的条件及其影响因素入手，确定并对比各影响因素的作用，从而掌握产生谐振过电压的关键因素，以获得从源头避免铁磁谐振发生的条件，不失为一个有效防御铁磁谐振风险的好办法。

研究表明，铁磁谐振源于系统容性参数和感性参数的不利配合。当系统正常运行时，因规划设计的原因，不会发生铁磁谐振；当发生了单相接地故障后，由于网络参数改变，短路电流造成铁磁式互感器铁心饱和而使其电感呈现非线性饱和特性，并与系统容性参数配合导致铁磁谐振的发生。影响系统中的感性参数和容性参数的因素很多，如故障类型[2]、短路点位置[3]、激发时刻[4]、过渡电阻、中性点接地方式、系统相间电容[5]、对地电容、互感器铁心材料和线路构成比例[6]等，上述影响铁磁谐振故障的部分因素被进行了分析，但对影响因素的量化作用程度以及各因素的重要度排序研究不足。

上述因素涉及系统本身的架构和参数、故障参数、电力设备类型等层面，各影响因素具有随机性且缺乏有效的数学表达方法，同时影响因素之间也存在相互作用和配合的关系，即系统采用的电磁式互感器铁心会受到短路电流的冲击而饱和，从而造成互感器电感下降，互感器铁心所采用的材料决定其饱和后的电感参数。系统故障后，故障位置影响了短路电流水平，也影响了电磁式互感器的铁心饱和程度，从而影响到互感器的电感，当系统本身所具有的电容参数与变化后的电感参数之间的关系达到共振的条件时，铁磁谐振故障发生。可见，对影响因素的作用程度进行量化，确定其中的关键影响因素，在设计、运行或调度过程中加以避免，将有助于电力部门防范与治理铁磁谐振故障。对影响系统感性参数和容性参数的因素进行分析的思路是在铁磁谐振历史事件参数的基础上，借助仿真模型对影响因素及其分布概率进行初步刻画，再借助模糊推理 Petri 网特性对离散故障事件概率进行动态分析，最后结合事故树(Fault tree analysis，FTA)思想，对造成铁磁谐振故障的影响因素的重要度进行排序，在实际运行过程中加以关注，避免促成铁磁谐振故障，从而达到风险的提前预防。

近年来，Petri 网因为可以对离散事件动态系统建模，在并发事件描述方面具有独特优势，同时也可以很好地描述故障的产生和传播过程，因此常被用于研究电力系统的继电保护故障诊断[7-8]，模糊推理 Petri网(Fuzzy reasoning Petri net，FRPN)是在 Petri 网的基础上扩展的图形化的数学建模工具[9-11]，适合于人类知识的表示和人工智能领域的求解，将其与FTA相结合具有推理简单和易于实现的优点。

有鉴于此，将FRPN与FTA结合，构建铁磁谐振关键影响因素分析模型，结合铁磁谐振故障多维实测数据和仿真模型，对影响小电流系统铁磁谐振过电压的诸多因素进行分析与对比，构建铁磁谐振及其影响因素之间的关系模型，最后利用 Petri 网的图形特性模糊推理算法和故障树思想计算影响因素重要度指标，并利用案例加以分析和验证，为及时发现影响铁磁谐振的关键因素提供参考。

2 铁磁谐振故障影响因素

2.1 铁磁谐振故障演变机理

小电流接地系统正常运行时，系统感抗大于容抗，不具备谐振条件，当系统发生扰动时，互感器中增大的励磁电流会造成铁心饱和而使其电感下降至与容抗相等，铁磁谐振故障发生，过程如图1所示。

由图1可知，促成电力系统发生铁磁谐振故障的因素由系统结构与参数、系统运行状态和设备参数三个方面构成。系统运行受到诸如单相铁磁谐振、外电路过电压故障、互感器空载合闸或母线不同期合闸等外界提供的能量激发，电流增大且流过互感器绕组，造成互感器铁心饱和，从而致使系统感性参数下降，当下降的感性参数与容性参数不利配合时，系统发生铁磁谐振。一般来说，铁磁谐振多发生在变压器空载或轻载工况下。

2.2 铁磁谐振故障事故树

线路构成、相间电容和接地电容会影响系统的容性参数。电容型互感器分为电容式和电磁式两种，这两种都会发生铁磁谐振[12-14]，中性点不接地系统较多采用电磁式互感器。

系统运行受外界能量激发会导致电流增大，不同的激发类型导致的感性参数变化有别。其中，单相接地短路电流水平与中性点参数高压侧直流电阻阻值呈负相关性，并与短路消除时间有关。因为故障消除时刻对应的各相电源电压的大小不同，导致电压恢复时释放的电荷量不同，造成 PT铁心的饱和程度有差异，从而产生大小不同的铁磁谐振过电压。外电路过电压故障和互感器空载合闸提供激发能量所产生的电流水平与变压器负载率呈负相关性，上述因扰动产生的增大的电流水平与互感器高压侧直流电阻均呈负相关关系。此外，过渡电阻、消弧线圈和中性点阻抗也会影响到所能量激发电流水平，进而限制铁磁谐振过电压水平。当增大的电流流过互感器绕组时，感性参数下降的程度受到互感器饱和程度的影响，而互感器饱和程度又受到电流水平和铁心材质的共同影响。当下降的感性参数与容性参数满足谐振条件时，铁磁谐振过电压故障发生。

根据上述分析，铁磁谐振故障事故树模型如图 2所示。

3 基于Petri网铁磁谐振关键影响因素

3.1 铁磁谐振过电压故障的Petri网

构建铁磁谐振故障模糊推理Petri网为

式中，P={P1,P2,…,Pn}代表库所，一部分表示影响系统感抗参数变化的参量，为初级库所，另一部分表示影响铁磁谐振过电压的参数，为目标库所；代表变迁状态或者规则集合，表示影响因素参数变化对目标库所的触发；为变迁或者规则的置信度，即各因素参数变化置信度，取值为 0～1，值越大，表示初级库所导致铁磁谐振故障的可能性越大；为输入矩阵，表示库所到变迁状态的有向弧，矩阵元素δij∈{0,1}为库所节点到变迁节点的模糊关系和权重，表示初始库所过渡到影响铁磁谐振过电压故障的状态，即变迁状态的权系数，当Pi是tj的输入时，为规则的输出矩阵(n×m)，oij∈ { 0,1}为变迁到库所的输出关系和结论可信度，意义与输入矩阵类似，表示影响因素促成了铁磁谐振发生的条件，即目标库所达到故障临界值的可信度；为库所的初始状态，其中θ0∈[0,1]。

铁磁谐振事故树因果关系的事件可以转换为Petri网络中库所的变迁，转换规则如表1所示。

表1 事故树与Petri推理规则对应表

表1中，x1、x2为事故树中的事件，在Petri网中为库所；c1、c2为变迁的置信度，具体数值需要结合配电网具体架构、参数和运行工况确定。

3.2 铁磁谐振故障模糊Petri推理算法

为了更好地推理铁磁谐振事件发生的过程与相关参数的参与程度，采用t范数和s范数代替传统模糊推理中的最大值和最小值概念[15-17]，规则如下所述。

t范数定义为t：[0; 1]×[0; 1]→[0; 1]，则对于每一个a，b，c∈[0; 1]，规则如下所述。

(1) 以1作为单位元素，即t(a，1)=a。

(2) 是单调的，即如果a≤b，则有t(a，c)≤t(b，c)。

(3) 服从交换律，即t(a，b)=t(b，a)。

(4) 服从关联律，即t{t(a，b)，c}=t{a，t(b，c)}。

s范数定义为s：[0; 1]×[0; 1]→[0; 1]，则对于每一个a，b，c∈ [0; 1]，规则如下所述。

(1) 以0作为单位元素，即s(a，0)=a。

(2) 是单调的，即，如果a≤b，则s(a，c)≤s(b，c)。

(3) 服从交换律，即s(a，b)=s(b，a)。

(4) 服从关联律，即s{s(a，b)，c}=s{a，s(b，c)}。

在上述规则基础上，利用neg算子进行下述模糊推理[11]。

式中，neg算子代表将命题取反，类似于逻辑非；1m为m列1矢量；k为推理阶次；vk为规则前提为假的可信度；ρk为规则前提为真的可信度；Qk为库所的k阶推理后的状态属性，其数值表示可信度。则有

根据式(3)推理可以得到第k步库所状态，推理终止条件为θ+1k=θk

3.3 铁磁谐振关键影响因素评估流程

(1) 针对某一区域电网实际参数，搭建仿真模型，计算各工况下的铁磁谐振故障参数集合，并以此为基础，构建影响因素与铁磁谐振关联模型。

(2) 整合影响铁磁谐过电压故障的系统架构与参数、设备参数和系统运行状态三方面因素，构建电压故障的参数集合，整理历史参数，初步确定各因素在铁磁谐振故障中的作用程度与临界阈值，并以此为依据，确定基本事件可信度。

(3) 构建Petri网络模型，利用Petri网模糊推理功能，确定相关影响因素特征值与导致故障的模糊可信度，构建接地网模糊故障树模型。

(4) 确定铁磁谐振故障过电压影响因素的割集，计算过电压指标。

(5) 根据Petri网，确定各影响因素对铁磁谐振故障的贡献。

关键影响因素辨识流程如图3所示。

4 算例分析

以某35 kV配电网实际参数为依据搭建模型，如图4所示。

由图4可知，系统主变型号为SSZ11-180000/220，绝缘水平为 750/950/395，互感器型号 JDZX9-35，为电磁式，铁心结构为单柱式，采用干式绝缘介质。配电网线路单位电阻R=0.4 Ω/km，单位电容为C=0.005 μF/km。互感器励磁特性参数如表2所示。

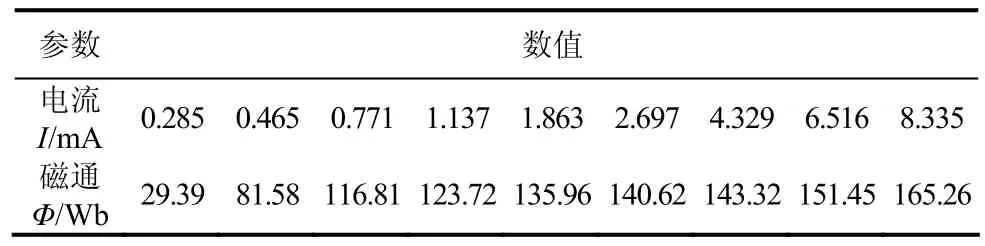
表2 互感器励磁特性参数

根据电网实际状况和故障记录，分析当故障激发类型、铁心类型、故障消除时刻、变压器中性点电阻、线路构成、过渡电阻、消弧线圈、补偿电容、接地电容和互感器高压侧中性点电阻等因素发生变化时的铁磁谐振现象，并据此确定主要因素变化情况，如表3所示。

根据步骤1～3，实现对该配电网进行铁磁谐振影响因素的关键性辨识。

第1步，根据表4参数范围，分别对系统进行仿真，以中性点电阻为例，当取值在0 Ω～1 000 kΩ变化时，得到的仿真结果如图5所示。

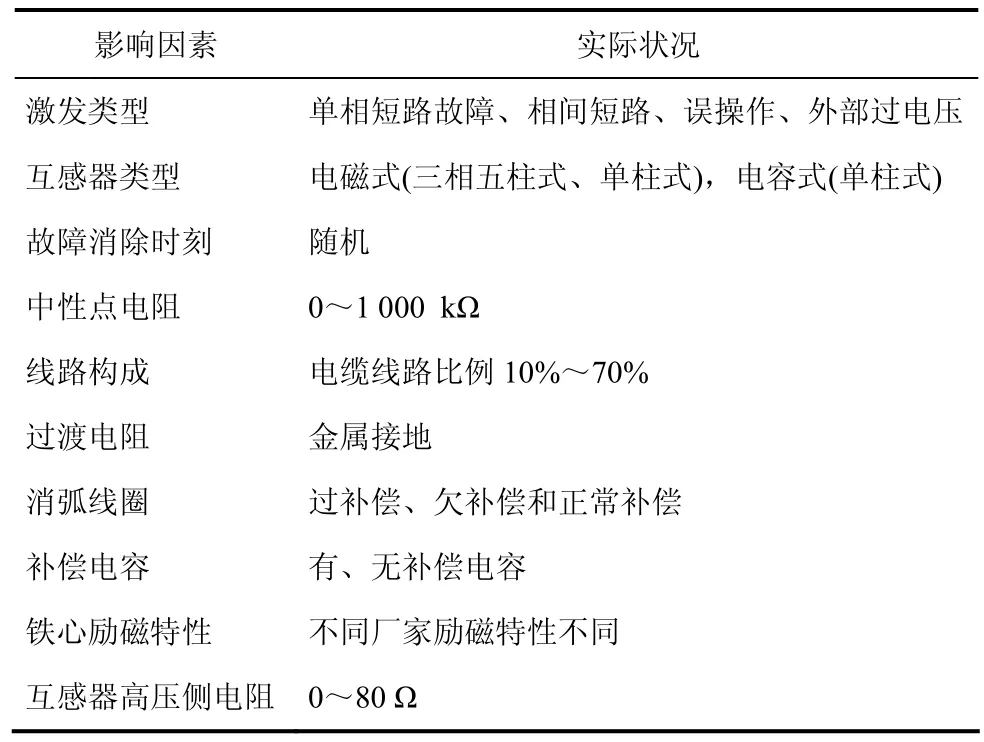
表3 区域配电网铁磁谐振主要影响因素

依次对其余影响参数变化进行仿真。

第2步，根据仿真数据构建铁磁谐振事故树模型，如图3所示。并确定系统参数初始Petri状态，Q0=[0.06,0.5,0.06,0.01,0.01,0.02,0.1,0.6,0.8,0.5,0.06,0.5,0.06]T。结合铁磁谐振过电压故障影响因素和图2所示的事故树模型，构建简化Petri网，如图6所示。

由图6可知，Pi(i=2,3,…,11)分别代表故障消除时刻(P2)、互感器类型(P3)、故障位置(P4)、变压器中性点电阻(P5)、线路构成(P6)、过渡电阻(P7)、消弧线圈(P8)、补偿电容(P9)、激发类型(P10)和互感器高压侧中性点电阻(P11)等因素，为初级库所；P0和P1分别代表系统感抗和系统容抗，为中级库所；P12表示铁磁谐振过电压，为高级库所。

有向箭头表示库所变迁的方向，ti(i=0,1,2,…,9,11,12)代表各库所的变迁，根据系统初始状况给定可信度为t={ti(i=0,1,2,…,9,11,12)| 0.95,0.8,0.8,0.9,0.6,0.9,0.85,0.7,0.7,0.95,0.7,0.9}。各低级库所到达阈值后，以一定的可信度(ti)变迁，对有向箭头所指的高一级库所产生不利影响。

第3步，将系统仿真初始条件和各工况下仿真结果数据利用t范数、s范数和式(1)规则计算，分别得到输入矩阵和输出矩阵如下。取C12×12=diag(0.9,0.6,0.4,0.7,0.5,0.2,0.3,0.8,0.2,0.1,0.8,0.3)为变迁或者规则的置信度，经推理得到库所状态如表4所示。

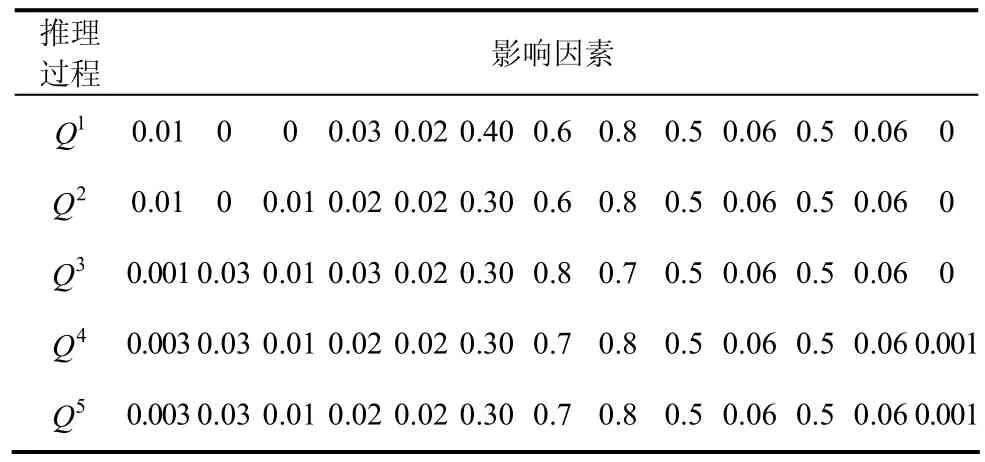
表4 模糊Petri网推理过程

最后，基于表4推理过程，计算仅有一个基本事件为真时的铁磁谐振过电压故障发生的可信度Con，结果如表5所示。

表5 库所的重要度指标

表5中Con还可表示基本事件对铁磁谐振故障的贡献重要度，由表5可见，P2、P5、P8、P11的贡献度最大，表示在该区域电网中，激发性故障消除时刻、中性点电阻、消弧线圈和互感器高压侧接电阻对铁磁谐振过电压具有关键性的影响。

目前，该区域电网已经在部分互感器高压侧装设了SiC非线性电阻，然而运行中仍出现互感器因铁磁谐振炸裂的现象，究其原因是SiC电阻的容量不足，无法完全消耗谐振能量而导致互感器炸裂。根据本研究成果，在互感器高压侧加装电阻为治理消谐措施的首选，但需要更换为更高容量的非线性电阻以代替SiC消谐器。经研究，该区域电网原有的一次消谐装置再替换为高容量ZnO非线性电阻后，再无铁磁谐振事件发生。此外，该地区电网也已经在部分电站加装了消弧线圈，然而运行中仍然出现单相接地短路故障消除后铁磁谐振问题，造成互感器的损坏。通过分析历史故障事件数据发现，所选取的参数不再具有抑制铁磁谐振的效果，因此还需要对消弧线圈的参数进行重新设定。激发故障消除时刻也是关键影响因素之一，若能结合保护装置的整定参数进行消谐，不用追加投资即可达到抑制效果，具有更大的经济性，然而如何进行保护参数的配合，还需要进一步地研究。

5 结论

本文提出了基于模糊 Petri网对影响铁磁谐振的关键性因素进行辨识的方法，发现互感器高压侧经非线性电阻接地、系统中性点加装消弧线圈和激发性故障消除时刻对铁磁谐振过电压具有关键性的影响，这一点对电力系统治理铁磁谐振治理有着重要的指导作用。

此外，试验过程中还发现在互感器一次侧加装非线性电阻消谐装置时，因消谐元件本身的特性存在设计能量不足的原因而导致铁磁谐振仍然发生的问题，这一点可以很好地解释电力系统中存在已经加装消谐装置但仍发生铁磁谐振的现象，对工程问题的解释具有参考价值。建议在采用电阻消谐装置时，首先根据配电网和互感器参数，模拟仿真铁磁谐振故障，计算非线性电阻抑制谐振时吸收的能量，再根据计算结果选择非线性电阻的同流容量，以确保消谐电阻的抑制效果。

从理论的角度提出了抑制和预防铁磁谐振的措施。当涉及到消谐装置时，因元件本身的特性存在差异，导致铁磁谐振的抑制效果存在很大的不同，结合具体装置的元件特性和参数进行影响因素的关键性评估，将更具有实际参考价值，这也将是下一步的研究内容。